LeetCode刷题记录(2)
文章目录
- 动态规划
-
- 01背包
- 背包问题
-
-
- [416. 分割等和子集](https://leetcode-cn.com/problems/partition-equal-subset-sum/)
- [1049. 最后一块石头的重量 II](https://leetcode-cn.com/problems/last-stone-weight-ii/)
- [494. 目标和](https://leetcode-cn.com/problems/target-sum/)
- 这里用的回溯暴搜[39. 组合总和](https://leetcode-cn.com/problems/combination-sum/)
-
- [322. 零钱兑换](https://leetcode-cn.com/problems/coin-change/)
- [53. 最大子序和](https://leetcode-cn.com/problems/maximum-subarray/)
- [300. 最长递增子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence/)
- [1143. 最长公共子序列](https://leetcode-cn.com/problems/longest-common-subsequence/)
- [718. 最长重复子数组](https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray/)
- 回溯
-
-
- [51. N 皇后](https://leetcode-cn.com/problems/n-queens/)
- [47. 全排列 II](https://leetcode-cn.com/problems/permutations-ii/)
- [869. 重新排序得到 2 的幂](https://leetcode-cn.com/problems/reordered-power-of-2/)
-
- 分治
-
-
- [53. 最大子序和](https://leetcode-cn.com/problems/maximum-subarray/)
-
- 链表(一定要多画图)
-
-
- [203. 移除链表元素](https://leetcode-cn.com/problems/remove-linked-list-elements/)
- [2. 两数相加](https://leetcode-cn.com/problems/add-two-numbers/)
- [160. 相交链表](https://leetcode-cn.com/problems/intersection-of-two-linked-lists/)
- **JZ52** **两个链表的第一个公共结点**
- [86. 分隔链表](https://leetcode-cn.com/problems/partition-list/)
- [234. 回文链表](https://leetcode-cn.com/problems/palindrome-linked-list/)
- [138. 复制带随机指针的链表](https://leetcode-cn.com/problems/copy-list-with-random-pointer/)
- **JZ25** **复杂链表的复制**
- **JZ15** **反转链表**
- **JZ3** **从尾到头打印链表**
- **JZ16** **合并两个排序的链表**
- **JZ14** **链表中倒数最后k个结点**
- **JZ23** **链表中环的入口结点**
- **JZ76** **删除链表中重复的结点**
-
- 栈
-
-
- [155. 最小栈](https://leetcode-cn.com/problems/min-stack/)
- [654. 最大二叉树](https://leetcode-cn.com/problems/maximum-binary-tree/)
- 654变种题(掌握)
- [739. 每日温度](https://leetcode-cn.com/problems/daily-temperatures/)
- [42. 接雨水](https://leetcode-cn.com/problems/trapping-rain-water/)
-
- 队列(包括双端队列)
-
-
- [239. 滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)
-
- 字符串
-
-
- [面试题 01.09. 字符串轮转](https://leetcode-cn.com/problems/string-rotation-lcci/)
- [572. 另一棵树的子树(二叉树的序列化)](https://leetcode-cn.com/problems/subtree-of-another-tree/)
- [242. 有效的字母异位词](https://leetcode-cn.com/problems/valid-anagram/)
- [151. 翻转字符串里的单词](https://leetcode-cn.com/problems/reverse-words-in-a-string/)
- [58. 最后一个单词的长度](https://leetcode-cn.com/problems/length-of-last-word/)
- [3. 无重复字符的最长子串](https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/)
- [1048. 最长字符串链](https://leetcode-cn.com/problems/longest-string-chain/)
- [32. 最长有效括号](https://leetcode-cn.com/problems/longest-valid-parentheses/)
- [79. 单词搜索](https://leetcode-cn.com/problems/word-search/)
-
- 树
-
-
- [124. 二叉树中的最大路径和](https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/)
-
- 排序
-
-
- [88. 合并两个有序数组](https://leetcode-cn.com/problems/merge-sorted-array/)
- [75. 颜色分类](https://leetcode-cn.com/problems/sort-colors/)
- [面试题 16.16. 部分排序](https://leetcode-cn.com/problems/sub-sort-lcci/)
- [164. 最大间距-排序](https://leetcode-cn.com/problems/maximum-gap/)
- [977. 有序数组的平方](https://leetcode-cn.com/problems/squares-of-a-sorted-array/)
-
- 其他类型
-
-
- **NC79** **丑数**
- **NC93** **设计LRU缓存结构**
-
- 十大排序算法
-
- 1、冒泡排序
- 2、选择排序
- 3、堆排序
-
- TopK问题(堆排序)
- 4、插入排序
- 5、归并排序
- 6、快速排序
- 7、希尔排序(对插入排序的优化)
- 8、计数排序
- 9、基数排序(个、十、百位)(基于计数排序)
- 10、桶排序(自定义规则)
- 二叉树遍历
- KMP算法(字符串匹配)
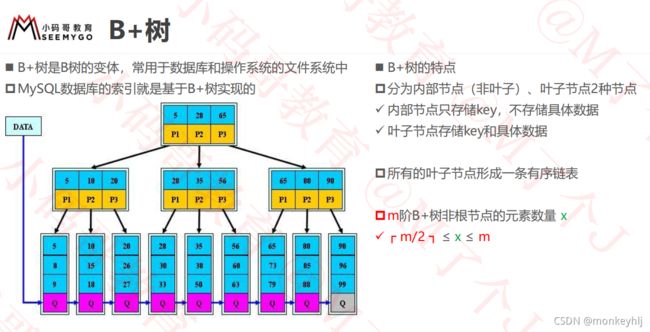
- B+树(MySQL)
动态规划
01背包
背包问题
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
class Solution {
public boolean canPartition(int[] nums) {
int mid = 0;
for(int i=0;i<nums.length;i++){
mid = mid + nums[i];
}
if(mid % 2 == 1) return false;
mid = mid / 2;
int[] dp = new int[10001];
for(int i=0;i<nums.length;i++){ //0-1背包问题
for(int j=mid;j>=nums[i];j--){
dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
if(dp[mid] == mid){
return true;
}
return false;
}
}
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
class Solution {
public int lastStoneWeightII(int[] stones) {
int mid = 0,sum = 0;
for(int i=0;i<stones.length;i++){
sum+=stones[i];
}
mid = sum / 2;
int[] dp = new int[15001];
for(int i=0;i<stones.length;i++){
for(int j = mid;j>=stones[i];j--){
dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return sum-dp[mid]-dp[mid];
}
}
494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
}
if(sum < target || sum < Math.abs(target)) return 0;
if((sum+target)%2==1) return 0;
int bagSize = (sum+target)/2;
int[] dp = new int[bagSize+1];
dp[0] = 1;
for(int i=0;i<nums.length;i++){
for(int j=bagSize;j>=nums[i];j--){
dp[j] += dp[j-nums[i]];
}
}
return dp[bagSize];
}
}
这里用的回溯暴搜39. 组合总和
给定一个无重复元素的正整数数组 candidates 和一个正整数 target ,找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同,则两种组合是唯一的。
对于给定的输入,保证和为 target 的唯一组合数少于 150 个。
输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]
class Solution {
List<List<Integer>> list = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
backtracking(candidates,target,0,0);
return list;
}
private void backtracking(int[] candidates,int target,int sum, int startIndex){
if(sum > target){
return;
}
if(sum == target){
list.add(new ArrayList<>(path));
return;
}
for(int i=startIndex;i<candidates.length;i++){
if((sum+candidates[i]) > target){ //剪枝
break;
}
sum+=candidates[i];
path.addLast(candidates[i]);
backtracking(candidates,target,sum,i);
sum-=candidates[i];
path.removeLast();
}
}
}
//参考:https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
class Solution {
public int coinChange(int[] coins, int amount) {
//dp(41) = 凑到41分需要的最少硬币个数
//dp(41-25) = 凑到41-25分需要的最少硬币个数
//dp(41) = dp(41-25)+1
if(amount < 1 || coins == null || coins.length == 0) return 0;
int[] dp = new int[amount+1];
for(int i=1;i<=amount;i++){
int min = Integer.MAX_VALUE;
for(int coin:coins){
if(i<coin || dp[i-coin] < 0) continue; //当dp[i-coin]已经是-1时则不要继续向下
min = Math.min(min,dp[i-coin]);
}
if(min == Integer.MAX_VALUE){
dp[i] = -1;
}else{
dp[i] = min+1;
}
}
return dp[amount];
}
}
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
class Solution {
public int maxSubArray(int[] nums) {
//dp[i] = 以nums[i]结尾的最大连续子序列和
if(nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length];
dp[0] = nums[0];
int max = dp[0];
for(int i=1;i<nums.length;i++){
if(dp[i-1] <= 0){
dp[i] = nums[i];
}else{
dp[i] = dp[i-1] + nums[i];
}
max = Math.max(dp[i],max);
}
return max;
}
}
//法2
class Solution {
public int maxSubArray(int[] nums) {
//dp[i] = 以nums[i]结尾的最大连续子序列和
if(nums == null || nums.length == 0) return 0;
int dp = nums[0]; //滚动数组原理,dp[i]只依赖于dp[i-1]
int max = dp;
for(int i=1;i<nums.length;i++){
if(dp <= 0){
dp = nums[i];
}else{
dp = dp + nums[i];
}
max = Math.max(dp,max);
}
return max;
}
}
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
class Solution {
public int lengthOfLIS(int[] nums) {
//dp[i] = 以nums[i]结尾的最长上升子序列的长度,初始值为1
if(nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length];
dp[0] = 1;
int maxLength = 1;
for(int i=1;i<nums.length;i++){
dp[i] = 1; //如果一个数比前面的数都大,则它的最长上升子序列的长度为1
for(int j=0;j<i;j++){
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i],dp[j]+1);
}
}
maxLength = Math.max(maxLength,dp[i]);
}
return maxLength;
}
}
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
//dp[i][j] = text1在i位置,text2在j位置两个字符串的最长子序列长度
if(text1 == null || text2 == null) return 0;
char[] char1 = text1.toCharArray();
char[] char2 = text2.toCharArray();
int[][] dp = new int[char1.length+1][char2.length+1];
for(int i=1;i<=char1.length;i++){
for(int j=1;j<=char2.length;j++){
if(char1[i-1] == char2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[char1.length][char2.length];
}
}
//法2---类似滚动数组
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
if(text1 == null || text2 == null) return 0;
char[] char1 = text1.toCharArray();
char[] char2 = text2.toCharArray();
char[] rowsNums = char1, colsNums = char2;
if (char1.length < char2.length) {
colsNums = char1;
rowsNums = char2;
}
int[] dp = new int[colsNums.length + 1];
for (int i = 1; i <= rowsNums.length; i++) {
int cur = 0;
for (int j = 1; j <= colsNums.length; j++) {
int leftTop = cur;
cur = dp[j];
if (rowsNums[i - 1] == colsNums[j - 1]) {
dp[j] = leftTop + 1;
} else {
dp[j] = Math.max(dp[j], dp[j - 1]);
}
}
}
return dp[colsNums.length];
}
}
718. 最长重复子数组
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1] 。
class Solution {
public int findLength(int[] nums1, int[] nums2) {
if(nums1.length == 0 || nums2.length == 0) return 0;
int[][] dp = new int[nums1.length+1][nums2.length+1];
int max = 0;
for(int i=1;i<=nums1.length;i++){
for(int j=1;j<=nums2.length;j++){
if(nums1[i-1] != nums2[j-1]){
continue;
}
dp[i][j] = dp[i-1][j-1]+1;
max = Math.max(max,dp[i][j]);
}
}
return max;
}
}
//法2
class Solution {
public int findLength(int[] nums1, int[] nums2) {
if(nums1.length == 0 || nums2.length == 0) return 0;
int[] rowArr,colArr;
if(nums1.length < nums2.length){
rowArr=nums2;
colArr=nums1;
}else{
rowArr=nums1;
colArr=nums2;
}
int[] dp = new int[colArr.length+1];
int max = 0;
for(int i=1;i<=rowArr.length;i++){
int cur=0;
for(int j=1;j<=colArr.length;j++){
int leftTop = cur; //保存左上角的数
cur = dp[j];
if(nums1[i-1] != nums2[j-1]){
dp[j] = 0;
}else{
dp[j] = leftTop+1;
max = Math.max(max,dp[j]);
}
}
}
return max;
}
}
47
5
72
回溯
51. N 皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
class Solution {
private int[] cols; //数组索引是行号,数组元素是列号
private List<List<String>> ways = new ArrayList<>(); //一共有多少种摆法
public List<List<String>> solveNQueens(int n) {
if(n < 1) return ways;
cols = new int[n];
place(0);
return ways;
}
//从第row行开始摆放皇后
public void place(int row){
if(row == cols.length){
//下面添加摆法
List<String> temp=new ArrayList<>();
for (int i = 0; i < cols.length; i++) {
StringBuffer s = new StringBuffer();
for (int col = 0; col < cols.length; col++) {
if (cols[i] == col) {
s.append('Q');
} else {
s.append('.');
}
}
temp.add(s.toString());
}
// ways++;
ways.add(temp);
// show();
return;
}
for(int col=0;col<cols.length;col++){
if(isValid(row,col)){
cols[row] = col; // 在第row行第col列摆放皇后
place(row+1);
}
}
}
//判断第row行第col列是否可以摆放皇后
public boolean isValid(int row,int col){
for(int i=0;i<row;i++){
// 第col列已经有皇后
if(cols[i] == col){
return false;
}
// 第i行的皇后跟第row行第col列格子处在同一斜线上
if(row-i == Math.abs(col-cols[i])){
return false;
}
}
return true;
}
// void show() {
// for (int row = 0; row < cols.length; row++) {
// for (int col = 0; col < cols.length; col++) {
// if (cols[row] == col) {
// System.out.print("1 ");
// } else {
// System.out.print("0 ");
// }
// }
// System.out.println();
// }
// System.out.println("------------------------------");
// }
}
47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
class Solution {
boolean[] vis;
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> ans = new ArrayList<List<Integer>>();
List<Integer> perm = new ArrayList<Integer>();
vis = new boolean[nums.length];
Arrays.sort(nums);
backtrack(nums, ans, 0, perm);
return ans;
}
public void backtrack(int[] nums,List<List<Integer>> ans,int index,List<Integer> perm){
if(index == nums.length){
ans.add(new ArrayList<Integer>(perm)); //new ArrayList
return;
}
for (int i = 0; i < nums.length; i++) {
if(vis[i] || (i>0 && nums[i]==nums[i-1] && !vis[i-1])){
continue;
}
perm.add(nums[i]);
vis[i] = true;
backtrack(nums,ans,index+1,perm);
vis[i] = false;
perm.remove(index);
}
}
}
869. 重新排序得到 2 的幂
给定正整数 N ,我们按任何顺序(包括原始顺序)将数字重新排序,注意其前导数字不能为零。
如果我们可以通过上述方式得到 2 的幂,返回 true;否则,返回 false。
输入:1
输出:true
输入:24
输出:false
class Solution {
boolean[] vis;
public boolean reorderedPowerOf2(int n) {
char[] nums = Integer.toString(n).toCharArray();
Arrays.sort(nums);
vis = new boolean[nums.length];
return backtrack(nums,0,0);
}
public boolean backtrack(char[] nums,int index,int num){
if(index == nums.length){
return isPowerOfTwo(num);
}
for(int i=0;i<nums.length;i++){
if((num == 0 && nums[i]=='0') || vis[i] || (i>0 && nums[i]==nums[i-1] && !vis[i-1])){
continue;
}
vis[i] = true;
if(backtrack(nums,index+1,num*10+nums[i]-'0')){
return true;
}
vis[i]=false;
}
return false;
}
public boolean isPowerOfTwo(int n){
return (n & (n-1)) == 0;
}
}
分治
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
class Solution {
public int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0) return 0;
return maxSub(nums,0,nums.length);
}
public int maxSub(int[] nums,int begin,int end){
if(end - begin < 2) return nums[begin];
int mid = (begin + end) >> 1;
int leftMax = Integer.MIN_VALUE;
int leftSum = 0;
for(int i=mid-1;i>=begin;i--){ //从中间到前面,因为中心分割线那里可能产生左+右的最大值
leftSum += nums[i];
leftMax = Math.max(leftMax,leftSum);
}
int rightMax = Integer.MIN_VALUE;
int rightSum = 0;
for(int i=mid;i<end;i++){
rightSum += nums[i];
rightMax = Math.max(rightMax,rightSum);
}
return Math.max(leftMax+rightMax,Math.max(maxSub(nums,begin,mid),maxSub(nums,mid,end)));
}
}
//更简单的做法--类似贪心算法
class Solution {
public int maxSubArray(int[] nums) {
int maxNum = nums[0];
int addNum = 0;
for(int i =0 ; i < nums.length; i ++){
addNum += nums[i];
maxNum = Math.max(maxNum,addNum);
if(addNum < 0){
addNum = 0;
}
}
return maxNum;
}
}
链表(一定要多画图)
虚拟头节点、快慢指针、多指针…
链表节点的插入、删除;反转一个链表;快慢指针求中心节点;计算链表的长度…
203. 移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
![]()
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
class Solution {
public ListNode removeElements(ListNode head, int val) {
if(head == null) return null;
ListNode dummyHead = new ListNode(0);
ListNode cur = dummyHead;
while(head != null){ //遍历整个链表
if(head.val != val){
cur.next = head;
cur = head;
}
head = head.next;
}
cur.next = null;
return dummyHead.next;
}
}
2. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode res = new ListNode(0);
ListNode cur = res;
int temp = 0;
while(l1 != null || l2 != null){
int v1 = (l1==null) ? 0:l1.val;
int v2 = (l2==null) ? 0:l2.val;
int sum = v1 + v2 + temp;
temp = sum / 10;
ListNode node = new ListNode(sum%10);
cur.next = node;
cur = node;
l1 = (l1==null)?null:l1.next;
l2 = (l2==null)?null:l2.next;
}
if(temp != 0){
ListNode head = new ListNode(temp);
cur.next = head;
}
return res.next;
}
}
160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
![]()
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA == null || headB == null) return null;
ListNode curA = headA,curB = headB;
while(curA != curB){
curA = (curA!=null)?curA.next:headB;
curB = (curB!=null)?curB.next:headA;
}
return curA;
}
}
//解法2:HashSet
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> visited = new HashSet<ListNode>();
ListNode temp = headA;
while (temp != null) {
visited.add(temp);
temp = temp.next;
}
temp = headB;
while (temp != null) {
if (visited.contains(temp)) {
return temp;
}
temp = temp.next;
}
return null;
}
}
JZ52 两个链表的第一个公共结点
输入两个无环的单向链表,找出它们的第一个公共结点,如果没有公共节点则返回空。
看下面的链表例子:
0-1-2-3-4-5-null
a-b-4-5-null
代码的ifelse语句,对于某个指针p1来说,其实就是让它跑了连接好的的链表,长度就变成一样了。
如果有公共结点,那么指针一起走到末尾的部分,也就一定会重叠。看看下面指针的路径吧。
p1: 0-1-2-3-4-5-null(此时遇到ifelse)-a-b-4-5-null
p2:a-b-4-5-null(此时遇到ifelse)0-1-2-3-4-5-null
因此,两个指针所要遍历的链表就长度一样了!
如果两个链表存在公共结点,那么p1就是该结点,如果不存在那么p1将会是null。
public class Solution {
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
if(pHead1 == null || pHead2 == null)return null;
ListNode p1 = pHead1;
ListNode p2 = pHead2;
while(p1!=p2){
p1 = p1.next;
p2 = p2.next;
if(p1!=p2){
if(p1==null) p1=pHead2;
if(p2 == null)p2 = pHead1;
}
}
return p1;
}
}
86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
![]()
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
class Solution {
public ListNode partition(ListNode head, int x) {
if(head == null) return head;
ListNode leftHead = new ListNode(0);
ListNode leftTail = leftHead;
ListNode rightHead = new ListNode(0);
ListNode rightTail = rightHead;
while(head!=null){
if(head.val < x){
leftTail.next = head;
leftTail = head;
}else{
rightTail.next = head;
rightTail = head;
}
head = head.next;
}
leftTail.next = rightHead.next;
rightTail.next = null;
return leftHead.next;
}
}
234. 回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
输入:head = [1,2,2,1]
输出:true
class Solution {
public boolean isPalindrome(ListNode head) {
if(head == null || head.next == null) return true;
if(head.next.next == null) return head.val == head.next.val;
//找到中间的节点
ListNode mid = middleNode(head);
//翻转右半部分(中间节点的右边部分)
ListNode rHead = reverseList(mid.next);
ListNode lHead = head;
//从lHead、rHead出发,判断是否为回文链表
while(rHead != null){
if(rHead.val != lHead.val) return false;
rHead = rHead.next;
lHead = lHead.next;
}
return true;
}
public ListNode middleNode(ListNode head){
if(head == null || head.next == null) return head;
ListNode fast = head;
ListNode slow = head;
while(fast.next!=null && fast.next.next!=null){
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
public ListNode reverseList(ListNode head){
if(head == null || head.next == null) return head;
ListNode cur = head;
ListNode newHead = null;
while(cur!=null){
ListNode temp = cur.next;
cur.next = newHead;
newHead = cur;
cur = temp;
}
return newHead;
}
}
//解法2:更简单
class Solution {
public boolean isPalindrome(ListNode head) {
List<Integer> vals = new ArrayList<Integer>();
// 将链表的值复制到数组中
ListNode currentNode = head;
while (currentNode != null) {
vals.add(currentNode.val);
currentNode = currentNode.next;
}
// 使用双指针判断是否回文
int front = 0;
int back = vals.size() - 1;
while (front < back) {
if (!vals.get(front).equals(vals.get(back))) {
return false;
}
front++;
back--;
}
return true;
}
}
138. 复制带随机指针的链表
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
![]()
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
class Solution {
public Node copyRandomList(Node head) {
if(head == null) return head;
Map<Node,Node> map = new HashMap<>(); //将每个节点用HashMap存储起来
Node p = head;
while(p!=null){
Node node = new Node(p.val);
map.put(p,node);
p = p.next;
}
p=head;
while(p!=null){
Node newNode = map.get(p);
if(newNode.next == null){
newNode.next = map.get(p.next);
}
if(newNode.random == null){
newNode.random = map.get(p.random);
}
p = p.next;
}
return map.get(head);
}
}
JZ25 复杂链表的复制
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针random指向一个随机节点),请对此链表进行深拷贝,并返回拷贝后的头结点。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)。 下图是一个含有5个结点的复杂链表。图中实线箭头表示next指针,虚线箭头表示random指针。为简单起见,指向null的指针没有画出。
输入:
{1,2,3,4,5,3,5,#,2,#}
返回值:
{1,2,3,4,5,3,5,#,2,#}
/*
public class RandomListNode {
int label;
RandomListNode next = null;
RandomListNode random = null;
RandomListNode(int label) {
this.label = label;
}
}
*/
import java.util.Map;
import java.util.HashMap;
public class Solution {
public RandomListNode Clone(RandomListNode pHead) {
if(pHead == null) return null;
Map<RandomListNode,RandomListNode> map = new HashMap<>();
RandomListNode newHead = null;
RandomListNode p = pHead;
RandomListNode q = null;
while(p!=null){
if(newHead == null){
newHead = new RandomListNode(pHead.label);
q = newHead;
map.put(pHead,newHead);
}else{
if(p.next != null && map.containsKey(p.next)){
q.next = map.get(p.next);
}else{
if(p.next != null){
RandomListNode temp = new RandomListNode(p.next.label);
map.put(p.next,temp);
q.next = temp;
}
}
if(p.random != null && map.containsKey(p.random)){
q.random = map.get(p.random);
}else{
if(p.random != null){
RandomListNode temp = new RandomListNode(p.random.label);
map.put(p.random,temp);
q.random = temp;
}
}
p = p.next;
q = q.next;
}
}
return newHead;
}
}
JZ15 反转链表
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}*/
public class Solution {
public ListNode ReverseList(ListNode head) {
// if(head == null || head.next == null) return head; //递归
// ListNode newHead = ReverseList(head.next);
// head.next.next = head;
// head.next = null;
// return newHead;
ListNode cur = head; //迭代
ListNode pre = null;
while(cur != null){
ListNode temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
}
return pre;
}
}
JZ3 从尾到头打印链表
import java.util.ArrayList;
import java.util.Collections;
public class Solution {
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> list = new ArrayList<>();
ListNode cur = listNode;
while(cur != null){
list.add(cur.val);
cur = cur.next;
}
Collections.reverse(list);
return list;
// ArrayList list = new ArrayList<>();
// ListNode tmp = listNode;
// while(tmp!=null){
// list.add(0,tmp.val);
// tmp = tmp.next;
// }
// return list;
}
}
JZ16 合并两个排序的链表
输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围: 0 \le n \le 10000≤n≤1000,-1000 \le 节点值 \le 1000−1000≤节点值≤1000
要求:空间复杂度 O(1)O(1),时间复杂度 O(n)O(n)
输入:
{1,3,5},{2,4,6}
返回值:
{1,2,3,4,5,6}
public class Solution {
public ListNode Merge(ListNode list1,ListNode list2) {
if(list1 == null){
return list2;
}
if(list2 == null){
return list1;
}
ListNode h = new ListNode(-1);
ListNode res = h;
while(list1 != null){
if(list2 != null){
if(list1.val <= list2.val){
res.next = list1;
list1 = list1.next;
}else{
res.next = list2;
list2 = list2.next;
}
}else{
res.next = list1;
list1 = list1.next;
}
res = res.next;
}
if(list2 != null){ //链表,直接接在后面就好
res.next = list2;
}
return h.next;
// ListNode h = new ListNode(-1);
// ListNode cur = h;
// while(list1 != null && list2 !=null){
// if(list1.val<=list2.val){
// cur.next = list1;
// list1 = list1.next;
// }else{
// cur.next = list2;
// list2 = list2.next;
// }
// cur = cur.next;
// }
// if(list1!=null) cur.next = list1;
// if(list2!=null) cur.next = list2;
// return h.next;
}
}
JZ14 链表中倒数最后k个结点
输入一个长度为 n 的链表,设链表中的元素的值为 ai ,输出一个链表,该输出链表包含原链表中从倒数第 k 个结点至尾节点的全部节点。
如果该链表长度小于k,请返回一个长度为 0 的链表。
输入:
{1,2,3,4,5},3
返回值:
{3,4,5}
public class Solution {
public ListNode FindKthToTail (ListNode pHead, int k) {
ListNode first = pHead; //双指针,一开始没想到,真是绝绝子
for(int i=0;i<k;i++){
if(first == null) return null;
first = first.next;
}
ListNode secend = pHead;
while(first != null){
first = first.next;
secend = secend.next;
}
return secend;
}
}
public class Solution {
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
if(pHead1 == null || pHead2 == null)return null;
ListNode p1 = pHead1;
ListNode p2 = pHead2;
while(p1!=p2){
p1 = p1.next;
p2 = p2.next;
if(p1!=p2){
if(p1==null) p1=pHead2;
if(p2 == null)p2 = pHead1;
}
}
return p1;
}
}
JZ23 链表中环的入口结点
- 这题我们可以采用双指针解法,一快一慢指针。快指针每次跑两个element,慢指针每次跑一个。如果存在一个圈,总有一天,快指针是能追上慢指针的。
- 如下图所示,我们先找到快慢指针相遇的点,p。我们再假设,环的入口在点q,从头节点到点q距离为A,q p两点间距离为B,p q两点间距离为C。
- 因为快指针是慢指针的两倍速,且他们在p点相遇,则我们可以得到等式 2(A+B) = A+B+C+B. (感谢评论区大佬们的改正,此处应为:*如果环前面的链表很长,而环短,那么快指针进入环以后可能转了好几圈(假设为n圈)才和慢指针相遇。但无论如何,慢指针在进入环的第一圈的时候就会和快的相遇。等式应更正为 2(A+B)= A+ nB + (n-1)C)*
- 由3的等式,我们可得,C = A。
- 这时,因为我们的slow指针已经在p,我们可以新建一个另外的指针,slow2,让他从头节点开始走,每次只走下一个,原slow指针继续保持原来的走法,和slow2同样,每次只走下一个。
- 我们期待着slow2和原slow指针的相遇,因为我们知道A=C,所以当他们相遇的点,一定是q了。
- 我们返回slow2或者slow任意一个节点即可,因为此刻他们指向的是同一个节点,即环的起始点,q。
public class Solution {
public ListNode EntryNodeOfLoop(ListNode pHead) {
if(pHead == null || pHead.next==null) return null;
ListNode fast = pHead;
ListNode slow = pHead;
while(fast!= null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(fast == slow){
ListNode p = pHead;
while(p!=slow){
p = p.next;
slow = slow.next;
}
return p;
}
}
return null;
}
}
JZ76 删除链表中重复的结点
在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。 例如,链表 1->2->3->3->4->4->5 处理后为 1->2->5
数据范围:链表长度满足 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存失败,源站可能有防盗链机制,建议将图片保存下来直接上传下上传(imnrAfGkmopJ-1669553577479)(https://www.nowcoder.com/equation?tex=1%20%5Cle%20n%20%5Cle%201000%20%5C)( https://www.nowcoder.com/equation?tex=1%20%5Cle%20n%20%5Cle%201000%20%5C)],链表中的值满足 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z7NU3ASm-1635769557480)(https://www.nowcoder.com/equation?tex=1%20%5Cle%20val%20%5Cle%201000%20%5C)]
进阶:空间复杂度 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Q7IVFvmT-1635769557480)(https://www.nowcoder.com/equation?tex=O(n)]%5C) ,时间复杂度 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jzUiaNE3-1635769557481)(https://www.nowcoder.com/equation?tex=O(n)]%20%5C)
输入:
{1,2,3,3,4,4,5}
返回值:
{1,2,5}
//暴力解法
import java.util.*;
public class Solution {
public ListNode deleteDuplication(ListNode pHead) {
Map<Integer,ListNode> map = new HashMap<>();
Set<Integer> set = new HashSet<>();
ListNode p = pHead;
while(p!=null){
if(map.containsKey(p.val)){
set.add(p.val);
}
map.put(p.val,p);
p=p.next;
}
ListNode newHead = new ListNode(0);
ListNode cur = newHead;
p=pHead;
Iterator<Integer> it = set.iterator();
Integer[] arr = new Integer[set.size()];
int i=0;
while(it.hasNext()){
arr[i] = it.next();
// System.out.println(arr[i]);
i++;
}
while(p!=null){
for(int j=0;j<arr.length;j++){
while(p!=null && p.val == arr[j]){
p=p.next;
}
}
if(p!=null){
// System.out.println(p.val);
cur.next = p;
cur=cur.next;
p=p.next;
}
}
cur.next=null;
return newHead.next==null?null:newHead.next;
}
}
//双指针解法
import java.util.*;
public class Solution {
public ListNode deleteDuplication(ListNode pHead) {
ListNode dummyHead = new ListNode(0);
ListNode cur = dummyHead;
while(pHead != null){
// 进入循环时,确保了 pHead 不会与上一节点相同
if(pHead.next == null || pHead.next.val != pHead.val){
cur.next = pHead;
cur = pHead;
}
// 如果 pHead 与下一节点相同,跳过相同节点(到达「连续相同一段」的最后一位)
while(pHead.next!=null && pHead.val==pHead.next.val){
pHead = pHead.next;
}
pHead = pHead.next;
}
cur.next=null;
return dummyHead.next;
}
}
栈
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
class MinStack {
private Stack<Integer> stack;
private Stack<Integer> minstack; //解法1:用双栈来存储
public MinStack() {
stack = new Stack<>();
minstack = new Stack<>();
}
public void push(int val) {
stack.push(val);
if(minstack.isEmpty()){
minstack.push(val);
}else{
minstack.push(Math.min(val,minstack.peek()));
}
}
public void pop() {
stack.pop();
minstack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return minstack.peek();
}
}
//解法2:使用节点存储(效率高)
class MinStack {
Node head;
public MinStack() {
head = new Node(0,Integer.MAX_VALUE,null);
}
public void push(int val) {
head = new Node(val,Math.min(val,head.min),head);
}
public void pop() {
head = head.next;
}
public int top() {
return head.val;
}
public int getMin() {
return head.min;
}
private static class Node{ //新建一个节点类
public int val;
public int min;
public Node next;
public Node(int val,int min,Node next){
this.val = val;
this.min = min;
this.next = next;
}
}
}
654. 最大二叉树
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下:
二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。
![]()
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
//二叉树很多问题都可以通过递归来解决
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
if(nums.length == 1) return new TreeNode(nums[0],null,null);
return findNode(nums,0,nums.length);
}
public TreeNode findNode(int[] nums,int li,int ri){
if(li == ri) return null;
int maxIndex = li;
for(int i=li+1;i<ri;i++){
if(nums[i] > nums[maxIndex]) maxIndex = i;
}
TreeNode head = new TreeNode(nums[maxIndex]);
head.left = findNode(nums,li,maxIndex);
head.right = findNode(nums,maxIndex+1,ri);
return head;
}
}
654变种题(掌握)
//题目变种:返回一个数组,数组中存放每个节点的父节点的索引值(掌握)===(用栈)
public int[] parentIndexes(int[] nums){
//1、扫描一遍所有的元素
//2、保持栈从栈底到栈顶是单调递减的
Stack<Integer> stack = new Stack<>();
int[] lis = new int[nums.length];
int[] ris = new int[nums.length];
//初始化
for(int i=0;i<nums.length;i++){
ris[i]=-1;
lis[i]=-1;
}
for(int i=0;i<nums.length;i++){
while(!stack.isEmpty() && nums[i] > nums[stack.peek()]){
ris[stack.pop()] = i;
}
lis[i] = stack.isEmpty()?-1:stack.peek();
stack.push(i);
}
//求父节点数组
int[] pis = new int[nums.length];
for(int i=0;i<nums.length;i++){
if(lis[i]==-1 && ris[i] == -1){
//i位置的是根节点
pis[i] = -1;
continue;
}
if(lis[i] = -1){
pis[i] = ris[i];
}else if(ris[i] = -1){
pis[i] = lis[i];
}else if(nums[lis[i]] < nums[ris[i]]){
pis[i] = lis[i];
}else{
pis[i] = ris[i];
}
}
return pis;
}
739. 每日温度
请根据每日 气温 列表 temperatures ,请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
//跟上面变种题解法相似
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
if(temperatures.length == 1) return new int[] {0};
int[] ris = new int[temperatures.length];
Stack<Integer> stack = new Stack<>();
for(int i=0;i<temperatures.length;i++){
while(!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]){
int t = stack.pop();
ris[t] = i-t;
}
stack.push(i);
}
return ris;
}
}
//倒推法:类似与动态规划的思想
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
if(temperatures.length == 0) return null;
int[] res = new int[temperatures.length];
for(int i=temperatures.length-2;i>=0;i--){
int j=i+1;
while(true){
if(temperatures[i] < temperatures[j]){
res[i] = j-i;
break;
}else if(res[j] == 0){
res[i] = 0;
break;
}
//当temperatures[i] == temperatures[j]的时候
j = j + res[j];
}
}
return res;
}
}
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
![]()
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
//参见官方:https://leetcode-cn.com/problems/trapping-rain-water/solution/jie-yu-shui-by-leetcode-solution-tuvc/
//解法1:单调递减栈(采用上方所写方法)
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n<2) return 0;
int res = 0;
Stack<Integer> stack = new Stack<>(); //单调递减栈
for(int i=0;i<n;i++){
while(!stack.isEmpty() && height[i] > height[stack.peek()]){
int top = stack.pop();
if(stack.isEmpty()) break;
int left = stack.peek();
int curwidth = i-left-1; //坑宽度
int curheight = Math.min(height[left],height[i]) - height[top]; //坑高度
res += curwidth * curheight;
}
stack.push(i);
}
return res;
}
}
//解法2:双指针(最好)
class Solution {
public int trap(int[] height) {
int n = height.length;
if(n<2) return 0;
int res = 0;
int left = 0,right = n-1;
int leftMax = 0,rightMax = 0;
while(left < right){
leftMax = Math.max(leftMax,height[left]);
rightMax = Math.max(rightMax,height[right]);
if(height[left] < height[right]){ //如果左边小于右边
res+=leftMax-height[left];
left++;
}else{
res+=rightMax-height[right];
right--;
}
}
return res;
}
}
//解法3:动态规划
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int[] leftMax = new int[n];
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
int[] rightMax = new int[n];
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
}
队列(包括双端队列)
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(k==1) return nums;
int[] maxes = new int[nums.length-k+1];
Deque<Integer> deque = new LinkedList<>();//构建双端队列
for(int i=0;i<nums.length;i++){
//只要nums[队尾] <= nums[i],就删除队尾
while(!deque.isEmpty() && nums[deque.peekLast()] <= nums[i]){
deque.pollLast();
}
//将i加到队尾
deque.offerLast(i);
//检查窗口的索引是否合法
int w = i-k+1;
if(w<0) continue;
//检查队头的合法性
if(deque.peekFirst() < w){
//队头不合法(失效,不在滑动窗口索引范围内)
deque.pollFirst();
}
//设置窗口的最大值
maxes[w] = nums[deque.peekFirst()];
}
return maxes;
}
}
//暴力解法
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(k==1) return nums;
int[] maxes = new int[nums.length-k+1];
int maxIndex = 0;
//先求出前k个元素的最大值索引
for(int i=1;i<k;i++){
if(nums[i] > nums[maxIndex]) maxIndex = i;
}
//li是滑动窗口的最左索引
for(int li=0;li<maxes.length;li++){
//ri是滑动窗口的最右索引
int ri = li+k-1;
if(maxIndex < li){ //最大值的索引不在滑动窗口的合理范围内
maxIndex = li;
for(int i=li+1;i<=ri;i++){
if(nums[i] >= nums[maxIndex]) maxIndex = i;
}
}else if(nums[ri] >= nums[maxIndex]){ //最大值的索引在滑动窗口的合理范围内
maxIndex = ri;
}
maxes[li]=nums[maxIndex];
}
return maxes;
}
}
字符串
面试题 01.09. 字符串轮转
字符串轮转。给定两个字符串s1和s2,请编写代码检查s2是否为s1旋转而成(比如,waterbottle是erbottlewat旋转后的字符串)。
输入:s1 = "waterbottle", s2 = "erbottlewat"
输出:True
class Solution {
public boolean isFlipedString(String s1, String s2) {
if(s1 == null || s2 == null) return false;
if(s1.length() != s2.length()) return false;
return (s1+s1).contains(s2);
}
}
572. 另一棵树的子树(二叉树的序列化)
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
class Solution {
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null || subRoot == null) return false;
return postSerialize(root).contains(postSerialize(subRoot));
}
public String postSerialize(TreeNode node){ //序列化
// if(node == null) return null;
StringBuilder s = new StringBuilder();
postSerializeRealize(node,s);
return s.toString();
}
public void postSerializeRealize(TreeNode node,StringBuilder str){
if(node.left == null){
str.append("#!");
}else{
str.append(postSerialize(node.left));
}
if(node.right == null){
str.append("#!");
}else{
str.append(postSerialize(node.right));
}
str.append(node.val).append("!");
}
}
242. 有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
输入: s = "anagram", t = "nagaram"
输出: true
class Solution {
public boolean isAnagram(String s, String t) {
int n = s.length();
if(n != t.length()) return false;
int[] count = new int[26];
char[] sarr = s.toCharArray();
char[] tarr = t.toCharArray();
for(int i=0;i<n;i++){
count[sarr[i]-'a']++;
}
for(int i=0;i<n;i++){
if(--count[tarr[i]-'a'] < 0) return false;
}
return true;
}
}
151. 翻转字符串里的单词
给你一个字符串 s ,逐个翻转字符串中的所有 单词 。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
请你返回一个翻转 s 中单词顺序并用单个空格相连的字符串。
说明:
输入字符串 s 可以在前面、后面或者单词间包含多余的空格。
翻转后单词间应当仅用一个空格分隔。
翻转后的字符串中不应包含额外的空格。
输入:s = "the sky is blue"
输出:"blue is sky the"
class Solution {
public String reverseWords(String s) {
if(s.length() == 1) return s;
char[] arr = s.toCharArray();
//首先消除多余的空格
int len=0; //字符串最终的有效长度
int cur=0; //当前用来存放字符的位置
boolean prespace = true; //记录前一个字符是否为空格字符
for(int i=0;i<arr.length;i++){
if(arr[i] != ' '){ //char[i]是非空格字符
arr[cur++] = arr[i];
prespace = false;
}else if(prespace == false){ //char[i]是空格字符,char[i-1]是非空格字符
arr[cur++] = ' ';
prespace = true;
}
}
len = prespace?(cur-1):cur;
//对整个字符串进行逆序
reverse(arr,0,len);
//对每一个单词进行逆序
int space = -1; //前一个空格字符的位置(有-1位置有个假想的哨兵,就是一个假想的空格字符)
for(int i=0;i<len;i++){
if(arr[i] != ' ') continue;
reverse(arr,space+1,i);
space = i;
}
//翻转最后一个单词
reverse(arr,space+1,len);
return new String(arr,0,len);
}
public void reverse(char[] arr,int li,int ri){ //左闭右开
ri--;
while(li < ri){
char temp = arr[li];
arr[li] = arr[ri];
arr[ri] = temp;
li++;
ri--;
}
}
}
58. 最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中最后一个单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
输入:s = " fly me to the moon "
输出:4
class Solution {
public int lengthOfLastWord(String s) {
if(s.length() == 1) return 1;
char[] arr = s.toCharArray();
int si = arr.length;
int ei = arr.length;
boolean space = true;
for(int i=arr.length-1;i>=0;i--){
if(arr[i] == ' '){
if(!space){
break;
}
si--;
ei--;
}else{
si--;
space = false;
}
}
return ei-si;
}
}
//解法2
class Solution {
public int lengthOfLastWord(String s) {
int len;
int lastSpace = s.length() - 1;
while(lastSpace >= 0 && s.charAt(lastSpace) == ' ')
lastSpace--;
int start = lastSpace;
while(start >= 0 && s.charAt(start) != ' ')
start--;
len = lastSpace - start;
return len;
}
}
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oCh1J09X-1635946803818)(.\pics\image-20211103193012546.png)]
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
class Solution {
public int lengthOfLongestSubstring(String s) {
if(s==null || s.length()==0) return 0;
if(s.length()==1) return 1;
char[] arr = s.toCharArray();
//用来保存每一个字符上一次出现的位置
// Map prevIndexes = new HashMap<>();
// prevIndexes.put(arr[0],0);
int[] prevIndexes = new int[128]; //改进:用数组来存储
for(int i=0;i<prevIndexes.length;i++){
prevIndexes[i]=-1;
}
prevIndexes[arr[0]] = 0;
//以i-1位置字符结尾的最长不重复字符串的开始索引(最左索引)
int li=0;
int max=1;
for(int i=1;i<arr.length;i++){
//i位置字符上一次出现的位置
// Integer pi = prevIndexes.get(arr[i]);
// if(pi!=null && li<=pi){
// li = pi+1;
// }
int pi = prevIndexes[arr[i]];
if(li<=pi){
li = pi+1;
}
//存储这个字符出现的位置
// prevIndexes.put(arr[i],i);
prevIndexes[arr[i]] = i;
//求出最长不重复子串的长度
max = Math.max(max,i-li+1);
}
return max;
}
}
1048. 最长字符串链
给出一个单词列表,其中每个单词都由小写英文字母组成。
如果我们可以在 word1 的任何地方添加一个字母使其变成 word2,那么我们认为 word1 是 word2 的前身。例如,“abc” 是 “abac” 的前身。
词链是单词 [word_1, word_2, …, word_k] 组成的序列,k >= 1,其中 word_1 是 word_2 的前身,word_2 是 word_3 的前身,依此类推。
从给定单词列表 words 中选择单词组成词链,返回词链的最长可能长度。
输入:["a","b","ba","bca","bda","bdca"]
输出:4
解释:最长单词链之一为 "a","ba","bda","bdca"。
//动态规划
class Solution {
public int longestStrChain(String[] words) {
Arrays.sort(words, Comparator.comparingInt(String::length));
int n=words.length;
if(n == 1) return 1;
int[] dp = new int[n];
int res=0;
for(int i=0;i<n;i++){
String a=words[i];
for(int j=i+1;j<n;j++){
if(isPredecessor(a,words[j])){
dp[j] = Math.max(dp[j],dp[i]+1);
res = Math.max(res,dp[j]);
}
}
}
return res+1;
}
/**
* 判断a是否是b的前身 是返回true 如 "bda" 是"bdca"的前身
*/
private boolean isPredecessor(String a, String b) {
int m=a.length(),n=b.length();
if(m+1 != n) return false;
int i=0,j=0;
while(i<m && j<n){
if(a.charAt(i) == b.charAt(j)) i++;
j++;
}
return i==m;
}
}
32. 最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
//666,没想到的!!!
class Solution {
public int longestValidParentheses(String s) {
int n = s.length();
if(n<2) return 0;
char[] arr = s.toCharArray();
Stack<Integer> stack = new Stack<>(); //放索引
stack.push(-1);
int max=0;
for(int i=0;i<n;i++){
if(arr[i] == '('){
stack.push(i);
}else{
stack.pop();
if(stack.isEmpty()){
stack.push(i);
}else{
max = Math.max(max,i-stack.peek());
}
}
}
return max;
}
}
1143(见上)
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
//回溯
class Solution {
public boolean exist(char[][] board, String word) {
int h = board.length,w = board[0].length;
boolean[][] visited = new boolean[h][w];
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
boolean flag = check(board,visited,i,j,word,0);
if(flag){
return true;
}
}
}
return false;
}
public boolean check(char[][] board, boolean[][] visited, int i, int j, String s, int k){
if(board[i][j] != s.charAt(k)){
return false;
}else if(k == s.length()-1){
return true;
}
visited[i][j] = true;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
boolean result = false;
for(int[] dir:directions){
int newi = i+dir[0],newj = j+dir[1];
if(newi>=0 && newi < board.length && newj >= 0 && newj < board[0].length){
if(!visited[newi][newj]){
boolean flag = check(board,visited,newi,newj,s,k+1);
if(flag){
result = true;
break;
}
}
}
}
visited[i][j] = false;
return result;
}
}
739(见上)
树
124. 二叉树中的最大路径和
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
a
/ \
b c
1.b + a + c。
2.b + a + a 的父结点。
3.a + c + a 的父结点。
其中情况 1,表示如果不联络父结点的情况,或本身是根结点的情况。
这种情况是没法递归的,但是结果有可能是全局最大路径和。
情况 2 和 3,递归时计算 a+b 和 a+c,选择一个更优的方案返回,也就是上面说的递归后的最优解啦。
另外结点有可能是负值,最大和肯定就要想办法舍弃负值(max(0, x))(max(0,x))。
但是上面 3 种情况,无论哪种,a 作为联络点,都不能够舍弃。
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
class Solution {
int ans = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
calSum(root);
return ans;
}
public int calSum(TreeNode root){
if (root == null) return 0;
int left = Math.max(0, calSum(root.left));
int right = Math.max(0, calSum(root.right));
ans = Math.max(ans, left + right + root.val);
return Math.max(left,right)+root.val;
}
}
排序
88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int li=0,le=m,ri=0,re=n;
int ai=0;
int[] leftArr = new int[m];
for(int i=li;i<le;i++){
leftArr[i] = nums1[i];
}
for(int i=ri;i<re;i++){
nums1[m+i] = nums2[i];
}
while(li < le){
if(ri < re && nums2[ri] < leftArr[li]){
nums1[ai++] = nums2[ri++];
}else{
nums1[ai++] = leftArr[li++];
}
}
}
}
//法2
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
for (int i = 0; i != n; ++i) {
nums1[m + i] = nums2[i];
}
Arrays.sort(nums1);
}
}
//法3
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
//类似于归并排序
int i1 = m-1; //指向nums1(有数)的末尾
int i2 = n-1; //指向nums2的末尾
int cur = nums1.length-1; //指向nums1的末尾
while(i2 >= 0){
if(i1 >= 0 && nums1[i1] > nums2[i2]){
nums1[cur--] = nums1[i1--];
}else{ //nums1[i1] <= nums2[i2]
nums1[cur--] = nums2[i2--];
}
}
}
}
75. 颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
class Solution {
public void sortColors(int[] nums) {
// Arrays.sort(nums);
//采用三指针方法,头和尾分别放一指针,遍历用一指针
//你能想出一个仅使用常数空间的一趟扫描算法吗?
int first = 0;
int last = nums.length-1;
int cur = 0;
while(cur <= last){
if(nums[cur] == 0){ //遇到0,则跟前面first交换,因为前面已经遍历过了,要么是0要么是1,所以指针直接往下走
swap(nums,cur++,first++);
}else if(nums[cur] == 2){ //遇到2,则跟后面进行交换,同时还要继续比较该交换过来的值
swap(nums,cur,last--);
}else{ //遇到1则继续向下走
cur++;
}
}
}
public void swap(int[] nums,int a,int b){
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
面试题 16.16. 部分排序
给定一个整数数组,编写一个函数,找出索引m和n,只要将索引区间[m,n]的元素排好序,整个数组就是有序的。注意:n-m尽量最小,也就是说,找出符合条件的最短序列。函数返回值为[m,n],若不存在这样的m和n(例如整个数组是有序的),请返回[-1,-1]。
输入: [1,2,4,7,10,11,7,12,6,7,16,18,19]
输出: [3,9]
class Solution {
public int[] subSort(int[] array) {
if(array.length == 0) return new int[] {-1,-1};
//从左扫描到右寻找逆序对(逐渐变大)
int max = array[0];
//用来记录最右的那个逆序对的位置
int r = -1;
for(int i=1;i<=array.length-1;i++){
if(array[i] >= max){
max = array[i];
}else{
r = i;
}
}
//说明没有逆序对,则直接return
if(r == -1) return new int[] {-1,-1};
//从右扫描到左寻找逆序对(逐渐变小)
int min = array[array.length-1];
//用来记录最左的那个逆序对的位置
int l = -1;
for(int i=array.length-2;i>=0;i--){
if(array[i] <= min){
min = array[i];
}else{
l = i;
}
}
return new int[] {l,r};
}
}
164. 最大间距-排序
给定一个无序的数组,找出数组在排序之后,相邻元素之间最大的差值。
如果数组元素个数小于 2,则返回 0。
输入: [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。
class Solution {
public int maximumGap(int[] nums) {
if(nums.length < 2) return 0;
Arrays.sort(nums);
int max = nums[1] - nums[0];
for(int i=2;i<nums.length;i++){
int temp = nums[i] - nums[i-1];
if(temp > max){
max = temp;
}
}
return max;
}
}
977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
class Solution {
public int[] sortedSquares(int[] nums) {
//还是使用双指针的思想,一个指向头,一个指向尾,并用一个新数组来存放比较后的平方值
int head = 0;
int tail = nums.length-1;
int[] ans = new int[nums.length];
for(int i=nums.length-1;i>=0;i--){
if(nums[head]*nums[head] > nums[tail]*nums[tail]){
ans[i] = nums[head]*nums[head];
head++;
}else{
ans[i] = nums[tail]*nums[tail];
tail--;
}
}
return ans;
}
}
其他类型
NC79 丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第 n个丑数。
输入:
7
返回值:
8
import java.util.List;
import java.util.ArrayList;
public class Solution {
public int GetUglyNumber_Solution(int index) {
if(index < 7) return index;
int p2=0,p3=0,p5=0;
List<Integer> list = new ArrayList<>();
list.add(1);
for(int i=0;i<index;i++){
int uglyNumber = Math.min(list.get(p2) * 2,Math.min(list.get(p3) * 3,list.get(p5) * 5));
list.add(uglyNumber);
if(uglyNumber % 2 == 0) p2++;
if(uglyNumber % 3 == 0) p3++;
if(uglyNumber % 5 == 0) p5++;
}
return list.get(index-1);
}
}
NC93 设计LRU缓存结构
设计LRU(最近最少使用)缓存结构,该结构在构造时确定大小,假设大小为 k ,并有如下两个功能
-
set(key, value):将记录(key, value)插入该结构
-
get(key):返回key对应的value值
提示:
1.某个key的set或get操作一旦发生,认为这个key的记录成了最常使用的,然后都会刷新缓存。
2.当缓存的大小超过k时,移除最不经常使用的记录。
3.输入一个二维数组与k,二维数组每一维有2个或者3个数字,第1个数字为opt,第2,3个数字为key,value
若opt=1,接下来两个整数key, value,表示set(key, value)
若opt=2,接下来一个整数key,表示get(key),若key未出现过或已被移除,则返回-1
对于每个opt=2,输出一个答案
4.为了方便区分缓存里key与value,下面说明的缓存里key用""号包裹
要求:set和get操作复杂度均为 O(1)
输入:
[[1,1,1],[1,2,2],[1,3,2],[2,1],[1,4,4],[2,2]],3
返回值:
[1,-1]
说明:
[1,1,1],第一个1表示opt=1,要set(1,1),即将(1,1)插入缓存,缓存是{"1"=1}
[1,2,2],第一个1表示opt=1,要set(2,2),即将(2,2)插入缓存,缓存是{"1"=1,"2"=2}
[1,3,2],第一个1表示opt=1,要set(3,2),即将(3,2)插入缓存,缓存是{"1"=1,"2"=2,"3"=2}
[2,1],第一个2表示opt=2,要get(1),返回是[1],因为get(1)操作,缓存更新,缓存是{"2"=2,"3"=2,"1"=1}
[1,4,4],第一个1表示opt=1,要set(4,4),即将(4,4)插入缓存,但是缓存已经达到最大容量3,移除最不经常使用的{"2"=2},插入{"4"=4},缓存是{"3"=2,"1"=1,"4"=4}
[2,2],第一个2表示opt=2,要get(2),查找不到,返回是[1,-1]
import java.util.*;
public class Solution {
/**
* lru design
* @param operators int整型二维数组 the ops
* @param k int整型 the k
* @return int整型一维数组
*/
private Map<Integer,Node> map = new HashMap<>();
private Node head = new Node(-1,-1);
private Node tail = new Node(-1,-1);
private int k;
public int[] LRU (int[][] operators, int k) {
this.k = k;
head.next = tail;
tail.prev = head;
int len = (int)Arrays.stream(operators).filter(x -> x[0] == 2).count();
int[] res = new int[len];
for(int i=0,j=0;i<operators.length;i++){
if(operators[i][0] == 1){
set(operators[i][1],operators[i][2]);
}else{
res[j++] = get(operators[i][1]);
}
}
return res;
}
private void set(int key,int val){
if(get(key) > -1){
map.get(key).val = val;
}else{
if(map.size() == k){
int rk = tail.prev.key;
tail.prev.prev.next = tail;
tail.prev = tail.prev.prev;
map.remove(rk);
}
Node node = new Node(key,val);
map.put(key,node);
moveToHead(node);
}
}
private int get(int key){
if(map.containsKey(key)){
Node node = map.get(key);
node.prev.next = node.next;
node.next.prev = node.prev;
moveToHead(node);
return node.val;
}
return -1;
}
private void moveToHead(Node node){
node.next = head.next;
head.next.prev = node;
head.next = node;
node.prev = head;
}
static class Node{
int key,val;
Node prev,next;
public Node(int key,int val){
this.key = key;
this.val = val;
}
}
}
十大排序算法
1、冒泡排序
public void BuubleSort(Integer[] arr){
for(int end=arr.length-1;end>0;end--){
//boolean sorted = true; //优化:如果已经有序则break
int sortedIndex = 1; //优化2:记录下最后一次交换的index,说明后面序列已有序
for(int begin=1;begin<=arr.length;begin++){
if(arr[begin] < arr[begin-1]){
int temp = arr[begin];
arr[begin] = arr[begin-1];
arr[begin-1] = temp;
//sorted = false;
sortedIndex = begin;
}
}
//if(sorted) break;
end = sortedIndex;
}
}
2、选择排序
public void SelectSort(Integer[] arr){
for(int end=arr.length-1;end>0;end++){
int maxIndex = 0;
for(int begin=1;begin<=end;begin++){
if(arr[maxIndex] <= arr[begin]){
maxIndex = begin;
}
}
int temp = arr[maxIndex];
arr[maxIndex] = arr[end];
arr[end] = temp;
}
}
3、堆排序
Integer[] arr;
int heapSize = arr.length;
public void HeapSort(){
//原地建堆
//heapSize>>1表示把heapSize右移1位,相当于heapSize/2
for(int i=(heapSize >> 1)-1;i>=0;i--){
shiftDown(i);
}
while(heapSize > 1){
//交换堆顶元素和尾部元素
swap(0,--heapSize);
//对0位置进行shiftDown(恢复堆的性质)
shiftDown(0);
}
}
public void shiftDown(int index){
Integer element = arr[index];
int half = heapSize >> 1;
while(index < half){ // index必须是非叶子节点
// 默认是左边跟父节点比
int childIndex = (index << 1) + 1; //根据公式得来的(2i+1)
Integer child = arr[childIndex];
int rightIndex = childIndex + 1;
//如果右子节点存在且右子节点大于左子节点
if(rightIndex < heapSize && arr[rightIndex] > child){
child = arr[childIndex = rightIndex];
}
//该节点与其最大子节点比较
if(element > child){
break;
}
//否则用子节点覆盖父节点
arr[index] = child;
index = childIndex;
}
arr[index] = element;
}
TopK问题(堆排序)
给定一个长度为 n 的可能有重复值的数组,找出其中不去重的最小的 k 个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4(任意顺序皆可)。
import java.util.ArrayList;
public class Solution {
public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
ArrayList<Integer> list = new ArrayList<Integer>();
if(k==0) return list;
int[] arr = new int[k];
for(int i=0;i<k;i++){
arr[i]=input[i];
}
for(int i=(k >> 1)-1;i>=0;i--){
shiftDown(i,arr);
}
for(int i=k;i<input.length;i++){ //从第k个数开始和大顶堆的堆顶元素比较,如小于则替换,最后堆中的k个元素则是最小的
if(input[i] < arr[0]){
arr[0] = input[i];
shiftDown(0,arr);
}
}
for (int i = 0; i < arr.length; i++) {
list.add(arr[i]);
}
return list;
}
public void shiftDown(int index,int[] arr){ //下滤(构建大顶堆)
Integer element = arr[index];
int half = arr.length >> 1;
while(index < half){ // index必须是非叶子节点
// 默认是左边跟父节点比
int childIndex = (index << 1) + 1; //根据公式得来的(2i+1)
Integer child = arr[childIndex];
int rightIndex = childIndex + 1;
//如果右子节点存在且右子节点大于左子节点
if(rightIndex < arr.length && arr[rightIndex] > child){
child = arr[childIndex = rightIndex];
}
//该节点与其最大子节点比较
if(element > child){
break;
}
//否则用子节点覆盖父节点
arr[index] = child;
index = childIndex;
}
arr[index] = element;
}
}
4、插入排序
public void InsertSort(Integer[] arr){
for(int begin = 1;begin < arr.length;begin++){
int cur = begin;
int v = arr[cur];
while(cur > 0 && v < arr[cur-1]){
arr[cur] = arr[cur-1];
cur--;
}
arr[cur] = v;
// while(cur > 0 && arr[cur] < arr[cur-1]){
//int temp = arr[cur];
//arr[cur] = arr[cur-1];
//arr[cur-1] = temp;
//cur--;
//}
}
}
5、归并排序
int[] leftarr;
public void MergeSort(Integer[] arr){
sort(0,arr.length,arr);
}
public void sort(int begin,int end,Integer[] arr){
if(end-begin<2) return;
int mid = (end+begin) >> 1;
sort(begin,mid,arr);
sort(mid+1,end,arr);
merge(begin,end,arr);
}
public void merge(int begin,int mid,int end,Integer[] arr){
int li = 0,le = mid;
int ri = mid+1,re = end;
int ai = begin;
//将左边数组备份
for(int i=li;i<le;i++){
leftarr[i] = arr[begin+i];
}
while(li < le){
if(ri < re && leftarr[li] > arr[ri]){
arr[ai++] = arr[ri++];
}else{
arr[ai++] = leftarr[li++];
}
}
}
6、快速排序
public void QuickSort(Integer[] arr){
sort1(0,arr.length,arr);
sort2(0,arr.length-1,arr);
}
public void sort1(int begin,int end,Integer[] arr){
if(end-begin < 2) return;
// 确定轴点位置 O(n)
int mid = privotIndex1(begin,end,arr);
// 对子序列进行快速排序
sort1(begin,mid,arr);
sort1(mid+1,end,arr);
}
/**
* 构造出 [begin, end) 范围的轴点元素
* @return 轴点元素的最终位置
*/
public int privotIndex1(int begin,int end,Integer[] arr){
int privot = arr[begin];
end--;
while(begin < end){
while(begin < end){
if(arr[end] > privot){ // 右边元素 > 轴点元素
end--;
}else{
arr[begin] = arr[end];
begin++;
break;
}
}
while(begin < end){
if(arr[begin] < privot){ // 左边元素 < 轴点元素
begin++;
}else{
arr[end] = arr[begin];
end--;
break;
}
}
}
// 将轴点元素放入最终的位置
array[begin] = pivot;
// 返回轴点元素的位置
return begin;
}
//法2
public void sort2(int begin,int end,Integer[] arr){
if(end-begin < 2) return;
// 确定轴点位置 O(n)
int mid = privotIndex2(begin,end,arr);
// 对子序列进行快速排序
sort1(begin,mid-1,arr);
sort1(mid+1,end,arr);
}
public int privotIndex2(int begin,int end,Integer[] arr){
int privot = begin,index = privot+1;
for(int i=index;i<=end;i++){
if(arr[privot] > arr[i]){
int temp = arr[index];
arr[index] = arr[i];
arr[i] = temp;
index++;
}
}
int temp = arr[privot];
arr[privot] = arr[index-1];
arr[index-1] = temp;
return index-1;
}
7、希尔排序(对插入排序的优化)
public void ShellSort(Integer[] arr){
List<Integer> stepSequence = shellStepSequence(arr);
for(Integer step:stepSequence){
sort(arr,step);
}
}
public void sort(Integer[] arr,int step){
for(int col=0;col<step;col++){ //对第col列进行排序
//col、col+step、col+2*step、col+3*step
for(int begin=col+step;begin<arr.length;begin+=step){
int cur = begin;
while(cur>col && arr[cur] < arr[cur-step]){
int temp = arr[cur-step];
arr[cur-step] = arr[cur];
arr[cur] = temp;
cur-=step;
}
}
}
}
public List<Integer> shellStepSequence(Integer[] arr){
List<Integer> stepSequence = new ArrayList<>();
int step = arr.length;
while((step >>= 1) > 0){
stepSequence.add(step);
}
return stepSequence;
}
8、计数排序
public void CountingSort(Integer[] arr){
//找出最大值
int max = arr[0];
for(int i=0;i<arr.length;i++){
if(arr[i] > max){
max = arr[i];
}
}
//开辟内存空间,存储每个整数出现的次数
int[] counts = new int[max+1];
//统计每个整数出现的次数
for(int i=0;i<counts.length;i++){
count[arr[i]]++;
}
//根据整数的出现次数,对整数进行排序
int index = 0;
for(int i=0;i<counts.length;i++){
while(counts[i]- > 0){
arr[index++] = i;
}
}
}
//改进后实现=============================================
public void CountingSort(Integer[] arr){
//找出最大值和最小值
int max = arr[0];
int min = arr[0];
for(int i=0;i<arr.length;i++){
if(arr[i] > max){
max = arr[i];
}
if(arr[i] < min){
min = arr[i];
}
}
//开辟内存空间,存储次数
int[] counts = new int[max-min+1];
//统计每个整数出现的次数
for(int i=0;i<arr.length;i++){
count[arr[i]-min]++;
}
//累加次数
for(int i=1;i<counts.length;i++){
counts[i] += counts[i-1];
}
//从后往前遍历元素,将它放到有序数组中的合适位置
int[] newArray = new int[arr.length];
for(int i=arr.length-1;i>=0;i--){
newArray[--counts[arr[i]-min]] = arr[i];
}
//将有序数组赋值到arr
for(int i=0;i<arr.length;i++){
arr[i] = newArray[i];
}
}
9、基数排序(个、十、百位)(基于计数排序)
public void RadixSort(Integer[] arr){
//找出最大值
int max = arr[0];
for(int i=0;i<arr.length;i++){
if(arr[i] > max){
max = arr[i];
}
}
//max=593
//百位数:593 / 100 % 10 = 5
//十位数:593 / 10 % 10 = 9
//个位数:593 / 1 % 10 = 3
for(int divider=1;i<=max;divider*=10){
countingSort(arr,divider);
}
}
public void countingSort(int divider){
//开辟内存空间,存储次数
int[] counts = new int[10];
//统计每个整数出现的次数
for(int i=0;i<arr.length;i++){
count[arr[i] / divider % 10]++;
}
//累加次数
for(int i=1;i<counts.length;i++){
counts[i] += counts[i-1];
}
//从后往前遍历元素,将它放到有序数组中的合适位置
int[] newArray = new int[arr.length];
for(int i=arr.length-1;i>=0;i--){
newArray[--counts[arr[i] / divider % 10] = arr[i];
}
//将有序数组赋值到arr
for(int i=0;i<arr.length;i++){
arr[i] = newArray[i];
}
}
10、桶排序(自定义规则)
二叉树遍历
package binarytree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
public class Test {
//递归遍历的方式与非递归遍历的方式:
//一、递归的方式:
//1、先序遍历:
private static void preOrder1(Node root){
if(root == null) return;
System.out.print(root.value);
preOrder1(root.left);
preOrder1(root.right);
}
//2、中序遍历:
private static void midOrder1(Node root){
if(root == null) return;
midOrder1(root.left);
System.out.print(root.value);
midOrder1(root.right);
}
//3、后序遍历:
private static void postOrder1(Node root){
if(root == null) return;
postOrder1(root.left);
postOrder1(root.right);
System.out.print(root.value);
}
//二、非递归的方式:
//1、先序遍历:
private static void preOrder2(Node root){
if(root == null) return;
Stack<Node> stack = new Stack<>();//用栈来存储(先进后出)
stack.push(root);
while(!stack.isEmpty()){
Node node = stack.pop();
System.out.print(node.value);
if(node.right != null) stack.push(node.right);
if(node.left != null) stack.push(node.left);
}
}
//2、中序遍历
private static void midOrder2(Node root){
if(root == null) return;
Stack<Node> stack = new Stack<>();
Node cur = root;
while(!stack.isEmpty() || cur != null){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
Node node = stack.pop();
System.out.print(node.value);
if(node.right != null) cur= node.right;
}
}
//3、后序遍历:
private static void postOrder2(Node root){
if(root == null) return;
Stack<Node> stack = new Stack<>();
Stack<Node> stack2 = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
Node node = stack.pop();
stack2.push(node);
if(node.left != null) stack.push(node.left);
if(node.right != null) stack.push(node.right);
}
while(!stack2.isEmpty()){
System.out.print(stack2.pop().value);
}
}
//三、层序遍历
private static void bfs(Node root){
if(root == null) return;
Queue<Node> queue = new LinkedList<>();//用队列来存储(先进先出)
queue.add(root);
while(!queue.isEmpty()){
Node node = queue.poll();
System.out.print(node.value);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
}
private static List<List<String>> bfs2(Node root){
List<List<String>> res = new ArrayList<>();//存储节点(List里面套List)
Queue<Node> queue = new LinkedList<>();//用队列来存储(先进先出)
queue.add(root);
List<String> list;
while(!queue.isEmpty()){
int size = queue.size();
list = new ArrayList<>();
while(size-- > 0){
Node node = queue.poll();
list.add(node.value);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(list);
}
return res;
}
public static void main(String[] args) {
Node nodeA = new Node("A");
Node nodeB = new Node("B");
Node nodeC = new Node("C");
Node nodeD = new Node("D");
Node nodeE = new Node("E");
Node nodeF = new Node("F");
Node nodeG = new Node("G");
//构建二叉树
nodeA.left = nodeB;
nodeA.right = nodeC;
nodeB.left = nodeD;
nodeB.right = nodeE;
nodeC.right = nodeF;
nodeE.left = nodeG;
preOrder1(nodeA);
System.out.println();
midOrder1(nodeA);
System.out.println();
postOrder1(nodeA);
System.out.println();
preOrder2(nodeA);
System.out.println();
midOrder2(nodeA);
System.out.println();
postOrder2(nodeA);
System.out.println();
bfs(nodeA);
bfs2(nodeA);
}
public static class Node{ //节点
public String value;
public Node left;
public Node right;
public Node(String value){
this.value = value;
}
}
}