leetcode_刷题总结(c++)_动态规划

主要参考：
动态规划解题套路框架

动态规划

算法思想

动态规划是一种分治思想
分治（将原问题分解为若干子问题，自顶向下求解各问题，合并子问题的解，从而得到原问题的解）
动态规划（将原问题分解为若干子问题，自底向上，先求解最小的子问题，然后把结果存储在表格中，在求解大问题的子问题时，直接查询之前的表格，避免重复计算，空间换时间）

算法要素

（1）最优子结构
问题在最优解包含子问题的最优解。
（2）子问题重叠
有大量子问题是重叠的。

解题思路

（1）状态
确定维度，确定下标代表的值
（2）状态转移公式（递归公式）
（3）确定初始化条件
（4）从记忆化搜索的角度入手

如何划分状态

要么已知，要么通过状态确定下来
有效信息

背包问题：移步我另一个博客：leetcode_刷题总结_0/1背包类

模板

(1)明确 base case（初始化）
(2)明确「状态」
(3)明确「选择」
(4)定义 dp 数组/函数的含义

明确 base case -> 明确「状态」（状态）-> 明确「选择」（状态转移公式）-> 定义 dp 数组/函数的含义（初始化）

//自顶向下递归的动态规划
void dp(状态1, 状态2, ...){
    for(选择 in 所有可能的选择){
        //此时的状态已经因为做了选择而改变
        result = 求最值(result, dp(状态1, 状态2, ...))
    }
    return result

//自底向上迭代的动态规划
//初始化 base case
dp[0][0][...] = base case
//进行状态转移
for(状态1 in 状态1的所有取值)
{
    for(状态2 in 状态2的所有取值)
    {
        for ...
        {
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)
        }
	}
}

PS：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。

leetcode部分题目

（一）背包问题DP

请移步我另一篇博客：
leetcode_刷题总结(c++)_动态规划_背包类问题

（二） 线性DP

在线性空间上的递推
区间DP、线性DP的共同点:无遗漏的遍历所有可能的情况，从首元素或者尾元素开始思考。
每个问题进行分解时只会减少最后一个元素，起始端是固定不变的

(1)游戏问题

70. 爬楼梯

70. 爬楼梯
（1）状态
思考到最后一步的状态(第n个台阶）
dp[i]表示走第i个台阶的方法数

（2）状态转移公式（递归公式）
每走一次由两种选择：走1个台阶、走2个台阶

dp[i] = dp[i - 1] + dp[i - 2];

（3）初始化
dp[0]=1;dp[1]=1

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n+1);
        //需要一个数组来存储
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

55. 跳跃游戏

55. 跳跃游戏

思路：

解题：
（1）状态
dp[i]表示能否走到i位置

（2）状态转移公式（递归公式）

if(i+j<=n-1)
	dp[i+j]=true;

（3）初始化
dp[0]=true;

class Solution {
public:
    bool canJump(vector<int>& nums) {
        //记忆化搜索
        //用dp[i]表示能否走到i位置
        int n=nums.size();
        vector<bool> dp(n,false);
        dp[0]=true;//初始化
        for(int i=0;i<n;i++){
            if(dp[n-1]==true)
                break;
            if(nums[i]==0 || dp[i]==false)
                continue;
            for(int j=1;j<=nums[i];j++){
                if(i+j<=n-1){
                    dp[i+j]=true;
                    if(i+j==n-1)
                        return  dp[n-1];
                }         
            }
        }
        return dp[n-1];
    }

逆推法：
若能到达最后，那么必然存在一个最靠近终点的值能直达终点（即nums[i]>=end-i),再把最靠近终点的值看为终点（end=i)。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        //记忆化搜索
        int n=nums.size();
        int end=n-1;
        for(int i=n-2;i>=0;i--){//最后一个n-1位置的不用处理
            if(end-i<=nums[i])
                end=i;
            if(end==0)
                break;
        }
        return end==0;
    }
};

(2)子序列/子数组问题

子数组：一定是连续的
子序列：可以是不连续的

子数组（连续）

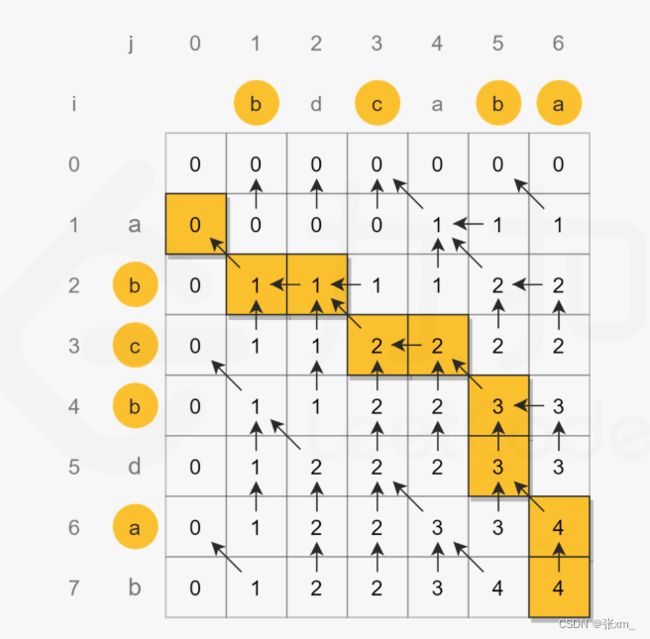
5. 最长回文子串；647. 回文子串

5. 最长回文子串

思路：
回文： 在n>2的情况下，一个回文去掉两头之后，剩下的部分依旧是回文
（1）两头相同： 由中间子串判断其是不是回文
（2）两头不同：不是回文

解题：
（1）状态
dp[i][j]=>s[i…j]是否是回文
（2）状态转移公式
若s[i]==s[j] 考虑s[i+1…j-1] ，
i = j ： 说明在区间内只有一个字符所以是回文子串即 dp[i][j] = true
i-j = 1：说明在区间内有两个相等的字符所以是回文子串即 dp[i][j] = true
i-j > 1：说明区间内字符数已经大于等于三个所以要判断此区间内是不是字符串需要将区间缩小即要判断[i+1,j-1]区间是否是回文串。若是则dp[i][j] = true；
最后就是当是回文串的时候记录最大长度和更新起始位置（和上题多了这个判断）
以上三种情况分析完了，那么递归公式如下：

if(s[i] == s[j]){
    if(j - i <= 1){ 
        dp[i][j] = 1;
    }
    else if(dp[i + 1][j - 1]){ 
        dp[i][j] = 1;
    }
    if(dp[i][j] && j - i + 1 > maxLen){
        maxLen = j - i + 1;
        begin = i;
    }
}
//简洁一点的写法
//j-i==1的情况 初始化时已经定义
if(s[i]==s[j] && (j-i<=2 || dp[i+1][j-1])){
	dp[i][j] =1;
}
if (dp[i][j] && j - i + 1 > maxLen) {
	maxLen = j - i + 1;
	begin = i;
}

（3）初始化
单个字符一定是回文 dp[i][j]=true

代码：

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.size();
        if(n<2)
            return s;
        int maxLen = 1;
        int begin = 0;
        vector<vector<int>> dp(n, vector<int>(n,0));
        for(int i=0; i<n; i++){//只有一个元素 一定为回文
            dp[i][i]=1;
        }
        //保证左下方位置先填完
        for (int i=n-1; i>= 0;i--){  
            for (int j=i; j<=n-1; j++){  
                if(s[i]==s[j] && (j-i<=2 || dp[i+1][j-1])){
                    dp[i][j] =1;
                }
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }

        return s.substr(begin,maxLen);

    }
};

647. 回文子串

class Solution {
public:
    int countSubstrings(string s) {
        int res = 0;
        // 定义dp数组 dp[i][j] 表示 【i，j】区间中的字符串是不是回文子串
        int n=s.size();
        vector<vector<int>> dp(n,vector<int>(n,0));
        // 注意遍历顺序
        // 注意，外层循环要倒着写，内层循环要正着写
        for (int i=n-1; i>= 0; i--) {  
            for (int j=i; j<n; j++) {
                if(s[i]==s[j] && (j-i<=2 || dp[i+1][j-1])){
                    dp[i][j] = true;
                    res++;
                }
            }
        }
        return res;
    }
};

718. 最长重复子数组

718. 最长重复子数组

思路：
（1）状态
nums1在中的 i 是否加入子数组
nums2在中的 j 是否加入子数组
dp[i][j]代表 nums1[0…i-1] nums2[0…j-1]位置中的最长重复子数组的长度

（2）状态转移公式
从后往前，从nums1和nums2中各抽出一个前缀数组，单看它们的末尾项是否为最终结果做出贡献（nums1[i-1]？=nums2[j-1]）

if(nums1[i-1]==nums2[j-1]){//做出贡献
	dp[i][j]=dp[i-1][j-1]+1;
}

（3）初始化
当 i=0 时，text1 [0:i] 为空，空字符串和任何字符串的最长重复子数组的长度都是 0，因此对任意0≤j≤n，dp[0][j]=0；
当 j=0 时，text2 [0:j] 为空，同理可得，对任意 0≤i≤m，dp[i][0]=0。

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int ans=0;
        vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));

        for(int i=1;i<=nums1.size();i++){
            for(int j=1;j<=nums2.size();j++){
                //nums1[i-1]与nums2[j-1]位置，相当于从0开始的dp i，j 位置
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                ans=fmax(ans,dp[i][j]);
            }
        }
        return ans;
    }
};

子序列（可不连续）

一般来说，这类问题都是让你求一个最长子序列，因为最短子序列就是一个字符嘛，没啥可问的。一旦涉及到子序列和最值，那几乎可以肯定，考察的是动态规划技巧，时间复杂度一般都是 O(n^2)。
原因很简单，你想想一个字符串，它的子序列有多少种可能？起码是指数级的吧，这种情况下，不用动态规划技巧，还想怎么着？

300. 最长递增子序列

300. 最长递增子序列

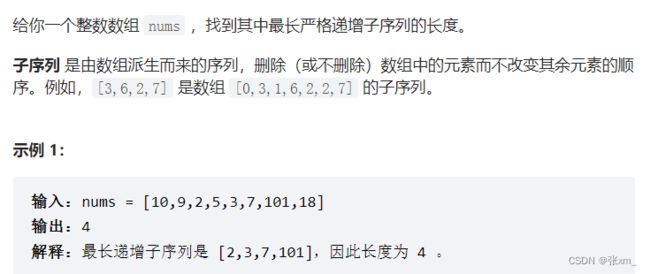
参考题解：https://leetcode.cn/problems/longest-increasing-subsequence/solution/di-zeng-zi-xu-lie-by-kino-58-ixhb/
思路：
后一步都与前一步有关=》可以拆分成子问题

思路：
（1）状态
dp[i] 为考虑前 i 个元素，以 nums[i] 这个数字结尾的最长上升子序列的长度，注意 nums[i] 必须被选取。

（2）状态转移公式
设 j∈[0,i)，考虑每轮计算新 dp[i] 时，遍历 [0,i) 列表区间，做以下判断：
当 nums[i] > nums[j] 时： nums[i] 可以接在 nums[j] 之后（此题要求严格递增），此情况下最长上升子序列长度为 dp[j] + 1 ；
当 nums[i] <= nums[j] 时： nums[i] 无法接在 nums[j] 之后，此情况上升子序列不成立，跳过。

if (nums[j] < nums[i]) {// 当后面大于前面的值 满足递增
	dp[i] = max(dp[i], dp[j] + 1);
}

（3）初始化
对任意 0≤i≤n， dp[i] =1，最小的长度子序列都是1，所以初始化都是1开始

（4）遍历顺序
dp（0… i-1) 位置的最长升序子序列 =>dp[i] ，=>遍历 i 一定是从前向后遍历，j 其实就是（0… i-1)，
遍历 i 的循环在外层，遍历 j 则在内层。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n=nums.size();
        int res=0;
        if (n == 0) {
            return 0;
        }
        //初始化 定义dp数组并初始化因为最小的长度子序列都是1所以初始化都是1开始
        vector<int> dp(n, 1);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {// 当后面大于前面的值 满足递增
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            if(dp[i]>res) 
                res = dp[i];
        }
        return res;
    }
};

1143. 最长公共子序列

1143. 最长公共子序列

思路：参考官方题解
有效信息：下标 先后顺序
（1）状态
text1在中的 i 是否为公共序列
text2在中的 j 是否为公共序列
dp[i][j]代表 text1[0…i-1] text2[0…j-1]位置中的最长公共子序列的长度

（2）状态转移公式
因子序列可以不连续，故仅考虑当前节点能不能加入
从后往前，考虑当前节点是否为最终结果做出贡献（text1[i-1]？=text2[j-1]）

if(text1[i-1]==text2[j-1]){//做出贡献
	dp[i][j]=dp[i-1][j-1]+1;
}
else{//wei做出贡献
	dp[i][j]=fmax(dp[i][j-1],dp[i-1][j]);
}

（3）初始化
当 i=0 时，text1 [0:i] 为空，空字符串和任何字符串的最长公共子序列的长度都是 0，因此对任意0≤j≤n，dp[0][j]=0；
当 j=0 时，text2 [0:j] 为空，同理可得，对任意 0≤i≤m，dp[i][0]=0。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int ans;
        vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));
        for(int i=1;i<=text1.size();i++){
            for(int j=1;j<=text2.size();j++){
                
                if(text1[i-1]==text2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=fmax(dp[i][j-1],dp[i-1][j]);
                }
            }
        }
        ans=dp[text1.size()][text2.size()];
        return ans;
    }
};

(3)网格问题

62. 不同路径

62. 不同路径

思路：
参考官方题解

有效信息：下标
（1）状态
dp[i][j] 代表 走到第[i][j]位置有几种不同的路径

（2）状态转移公式
两种情况：从上往下走、从左往右走

 dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

（3）初始化
一开始，只有一种走法
对任意 0≤i≤m，dp[i][0]=1；对任意 0≤j≤n，dp[0][j]=1。

二维dp：

class Solution {
public:
    int uniquePaths(int m, int n) {
        // dp二维数组
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int j = 0; j < n; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

一维dp：

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> dp(n,1);
        for (int j = 1; j < m; j++) {
            for (int i = 1; i < n; i++) {
                dp[i] += dp[i - 1];
            }
        }
        return dp[n - 1];    
    }
};

（三）区间DP

区间dp就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的 最优解进而得出整个大区间上最优解的dp算法。

区间DP、线性DP的共同点:无遗漏的遍历所有可能的情况，从首元素或者尾元素开始思考。

例如合并石头问题在分解成子问题的过程中，每个子问题的起始端和结尾端不是固定的，但是长度递减。
所以要按照长度递增的顺序进行区间DP。保证在求解每个大问题的时候，子问题都已经有解了。

区间DP模板：

for (int len = 1; len <= n; len++) {         // 区间长度
    for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
        int j = i + len - 1;                 // 区间终点
        if (len == 1) {
            dp[i][j] = 初始值
            continue;
        }

        for (int k = i; k < j; k++) {        // 枚举分割点，构造状态转移方程
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
        }
    }
}

282. 石子合并（AcWing）

282. 石子合并（AcWing）

参考;https://www.acwing.com/solution/content/13945/

思路：
限制了只能合并相邻的两堆，因此最后一步一定是左堆+右堆，然后分别需要左堆与右堆都是最优的（力气最小）。因为合并有（n-1）！的组合方式，因此用暴力法一定会超时，我们想到将每一种合并的最优结果记录，防止重复计算=》DP。

（1）状态
f(i,j)
集合：所有将[i,j]合并成一堆的方案的集合
属性：石子数的值（最小力气）

（2）状态转移公式
最后一步一定是左堆+右堆，因此可以选择左堆与右堆的分界点，作为依据来划分集合。
可以划分为（i),(i+1),…(k),…,(j-1)
每个子集求最小值，=》最后再取min，即全局最小值
取第k个子集进行分析：可以发现合并k的左边和k的右边互不影响
k的左边最小值=f(i,k)
k的右边最小值=f(k+1,j)
f[i][k] + f[k+1][j]代表的是合成[i,k]这一堆石子和合成[k+1,j]这一堆石子代价
s[j]-s[i-1]代表的合并[i,k] [k+1,j] 这两堆石子的代价(s[j]-s[i-1]为j到i所有石子的和）

前缀和可参考leetcode_刷题总结(c++)_前缀和

（3）初始化

 if (len == 1) {
	f[i][j] = 0;  // 边界初始化
	continue;
}

完整代码：

#include 
#include 
using namespace std;

const int N = 307;
int a[N], s[N];//s[]是全局变量，会自动初始化成0
int f[N][N];//f[][]是全局变量，会自动初始化成0

int main() {
    int n;
    cin >> n;

    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        s[i] += s[i - 1] + a[i];
    }

    memset(f, 0x3f, sizeof f);
    for (int len = 1; len <= n; len ++) { // len表示[i, j]的元素个数
        for (int i = 1; i + len - 1 <= n; i ++) {//左端点
            int j = i + len - 1; // 右端点
            if (len == 1) {
                f[i][j] = 0;  // 边界初始化
                continue;
            }
            for (int k = i; k <= j - 1; k ++) { //因为k是左半段的结尾，[k + 1, j]是右半段，k + 1必须<= j
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
            }
        }
    }
    cout << f[1][n] << endl;
    return 0;
}