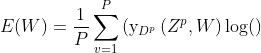深度学习实战——卷积神经网络/CNN实践(LeNet、Resnet)

      忆如完整项目/代码详见github：https://github.com/yiru1225（转载标明出处 勿白嫖 star for projects thanks）

系列文章目录

本系列博客重点在深度学习相关实践（有问题欢迎在评论区讨论指出，或直接私信联系我）。

第一章  深度学习实战——不同方式的模型部署（CNN、Yolo）_如何部署cnn_@李忆如的博客

第二章  深度学习实战——卷积神经网络实践

---

目录

系列文章目录

一、实验综述

1.实验工具及内容

2.实验数据

3.实验目标

4.实验步骤

二、卷积神经网络综述

1.卷积神经网络概念与原理

2.卷积神经网络发展历程

三、LeNet原理、实现与优化

1.LeNet原理

1.1 简介

1.2 数据集介绍

1.3 网络发展

1.4 网络解析

2.LeNet实现

2.1 代码实现与解析

2.2 代码测试

3.LeNet优化

3.1 超参数

3.2 优化与消融实验

Ⅰ、lr/Batch_size

Ⅱ、epoch

Ⅲ、激活函数/池化方式

Ⅳ、网络超参数

Ⅴ、最优参数组合

四、高级架构介绍与选择实现

1.AlexNet

2.VGG

3.NiN

4.ResNet

5.ResNet的实践

五、图像显著性与可视化诊断

1.图像显著性

2.特征可视化

2.1 CAM

2.2 Grad-CAM

2.3 其他特征可视化

3.CAM可视化诊断实践

4.其他可视化诊断拓展

六、总结 

1.实验结论 

2. 参考资料

---

梗概

本篇博客主要介绍几种卷积神经网络的原理，并进行了代码实践与优化，另外，使用了CAM、图像显著性检测等方法进行了模型的可视化诊断。（内附代码与数据集）。

---

一、实验综述

本章主要对实验思路、环境、步骤进行综述，梳理整个实验报告架构与思路，方便定位。

1.实验工具及内容

本次实验主要使用Pycharm完成几种卷积神经网络的代码编写与优化，并通过不同参数的消融实验采集数据分析后进行性能对比。另外，分别尝试使用CAM与其他MIT工具包中的显著性预测算法对模型进行可视化诊断，并同时在一些在线平台上做了预测。

2.实验数据

本次实验大部分数据来自卷积神经网络模型官方数据集，部分测试数据来源于网络。

3.实验目标

本次实验目标主要是深度剖析卷积神经网络的原理与模型定义，并了解不同参数的意义与对模型的贡献度（性能影响），通过实践完成不同模型、参数情况的性能对比与可视化诊断，指导真实项目开发中应用。

4.实验步骤

本次实验大致流程如表1所示：

表1 实验流程

1．实验思路综述

2.卷积神经网络综述

3.LetNet原理、实现与优化

4.高级架构介绍与选择实现

5.图像显著性与可视化诊断

二、卷积神经网络综述

本实验无论是实践LetNet、AlexNet还是其他高级架构，都属于卷积神经网络，故本章先对神经网络的概念与原理做一定综述，并简述其发展历程。

1.卷积神经网络概念与原理

卷积神经网络（Convolutional Neural Network，简称CNN）是一类前馈神经网络，是基于神经认知机和权重共享的卷积神经层（感受野衍生概念）被提出的，由于其具有局部区域连接、权值共享、降采样的结构特点，如今在图像处理领域有较好效果并并大量应用。

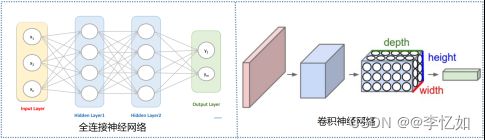
在此之前，一般使用全连接神经网络进行图像处理与其他人工智能任务，两种网络结构对比如图1所示，而全连接神经网络处理大图像图像时有以下三个明显的缺点：

1. 首先将图像展开为向量会丢失空间信息；
2. 其次参数过多效率低下，训练困难；
3. 同时大量的参数也很快会导致网络过拟合。

图1 两种神经网络结构对比

如图1所示，CNN中的各层中的神经元是3维排列的：宽度、高度和深度（深度指激活数据体的第三个维度），而将CNN的结构拆解，在原理实现上一般由输入层、卷积层（一般包含激活函数层）、池化（Pooling）层和全连接层各层叠加构建，各层简介如图表1：

图表1 CNN各层简介

输入层: 相关数据（集）的输入与读取

过程：

卷积层与激活函数层（应用中统称卷积层）： 主要就是使用卷积核进行特征提取和特征映射，由于卷积一般为线性运算，故需要使用激活函数（目前常用ReLU）增加非线性映射。

池化层：     主要作用体现在降采样：保留显著特征、降低特征维度，增大kernel的感受野，同时提供一定的旋转不变性。

全连接层（输出层）：     经过若干次卷积+激励+池化后，将多个特征图进行通过softmax等函数全连接并输出（与全连接神经网络类似），对于过拟合等现象会引入dropout、正则化等操作，还可以进行局部归一化（LRN）、数据增强，交叉验证，提前终止训练等操作，来增加鲁棒性。

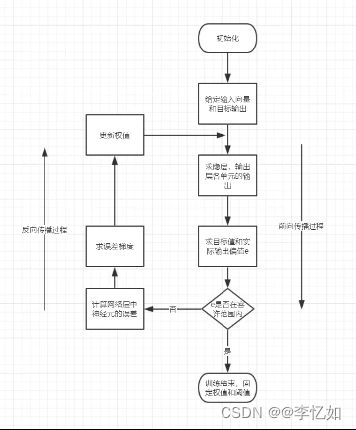
根据实验1中ML/DL任务综述我们知道人工智能任务中最重要的就是数据和模型，而对于CNN的模型训练，核心流程（与其他网络训练类似）如图2所示：

图2 CNN模型训练核心流程

Tips：CNN大类概念与核心原理解析到此结束，特定网络的解析在后文实践中详述。

2.卷积神经网络发展历程

本部分对CNN的发展历程做一个简述，经典的CNN网络发展可见图3：

图3 经典CNN的发展历程

Tips：本图仅统计2016及之前经典CNN网络。

根据图3，广义上最早的卷积神经网络是1998年的LeNet，但随着SVM等手工设计特征的出现沉寂。而因ReLU和dropout的提出，以及GPU和大数据带来的历史机遇，CNN在2012年迎来重大突破——提出AlexNet，至此，大量CNN网络结构被提出并广泛应用。而如今Transformer（Vision）在人工智能各领域的高速发展与优秀效果正使CNN面临危机。

三、LeNet原理、实现与优化

在上一章中我们对卷积神经网络进行了简单介绍，在本章正式进入CNN的实现与优化，主要将以最经典的CNN——LeNet为例探究不同实现/参数对效果的影响。

1.LeNet原理

1.1 简介

论文：Gradient-Based Learning Applied to Document Recognition

链接：Gradient-Based_Learning_Applied_to_Document_Recognition.pdf 

    根据论文、网络资料、个人理解，首先在本节对LeNet原理进行介绍与解析。

    背景：LeNet-5的设计主要是为了解决手写识别问题。那时传统的识别方案很多特征都是hand-crafted，识别的准确率很大程度上受制于所设计的特征，而且最大的问题在于手动设计特征对领域性先验知识的要求很高还耗时耗力，更别谈什么泛化能力，基本上只能针对特定领域。故本节同样以手写数字识别任务来介绍其原理。

1.2 数据集介绍

由于我们的原理介绍与后续实验都是基于手写数字识别任务，故在本部分对经典的数据集做一定介绍，以MNIST和Fashion-MNIST为例。

Ⅰ、MNIST：MNIST是一个著名的计算机视觉数据集，其包含各种手写数字图片（训练集中有60000个样本，测试集中有10000个样本，每个样本都是一张 28x28 像素的灰度手写数字图片），部分数据可视化如图4所示：

数据集下载：MNIST handwritten digit database,Ys 

图4 MNIST数据可视化（部分）

Ⅱ、Fashion-MNIST：Fashion-MNIST 是一个替代 MNIST 手写数字集的图像数据集，涵盖了来自 10 种类别的共 7 万个不同商品的正面图片，数据格式与MNIST完全一致，不需要改动任何网络代码，部分数据可视化如图5所示：

数据集下载：github-Fashion-MNIST.com

图5 Fashion-MNIST数据可视化（部分）

1.3 网络发展

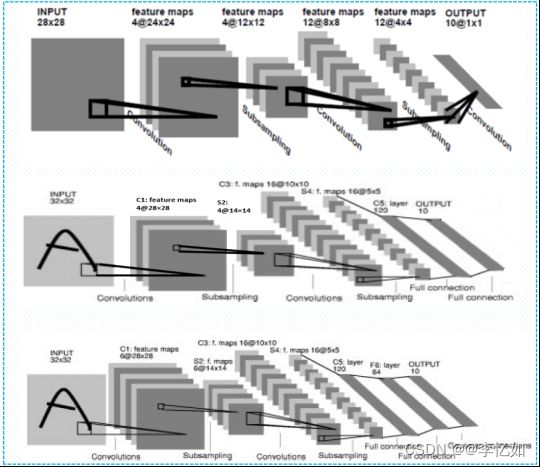
一般我们常说的LeNet是LeNet-5，而LeNet是一类网络结构（含1、4、5），在此对其网络发展及其之前发展做一定回顾（以手写数字识别为例），如图表2所示：

图表2 手写数字识别发展（至LeNet-5）

非CNN: 非CNN的识别过程在第一章第一节有简述，大致经历了简单线性分类器（每个输入像素值构成每个输出单元的加权和）->单隐藏层网络->双（多）隐藏层网络三个过程。

LeNet：     LeNet发展大致经历了LeNet-1、LeNet-4、LeNet-5三个部分（下图由上至下），网络层数变化为5->6->7，据图分析处理部分（卷积、池化）并未发生大变动，主要是输入、输出部分的格式与处理的变化，网络解析在后文详述。

1.4 网络解析

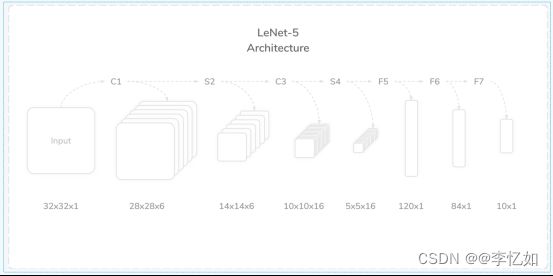
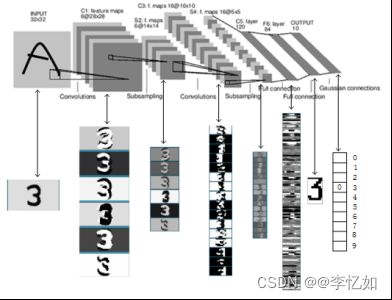
本部分我们对LeNet-5的网络架构进行深入解析，如图6所示，以便后续的实现与优化。

图6 LeNet-5网络架构

如图6所示，LeNet-5是一个7层卷积神经网络，包含C1、S2、C3、S4、C5/F5、F6、F7（C为卷积层，S为池化（pooling）层，F为全连接层），各层简介总结如图表3：

图表3 LeNet-5各层简介

输入层: 相关数据（集）的输入与读取，尺寸统一归一化为32*32

过程：

1、C1层：     Tips：LeNet激活函数默认为Sigmoid。 参数：num_kernels=6, kernel_size=5×5, padding=0, stride=1 补充：特征图大小计算如式1： 式1 特征图大小计算公式 对输入图像进行第一次卷积运算，得到6个C1特征图（6个大小为28*28的 feature maps, 32-5+1=28）。

2、S2层： Tips：LeNet默认使用平均池化。 参数：kernel_size=2×2, padding=0, stride=2 第一次卷积之后紧接着就是池化运算，得到了6个14*14的特征图（28/2=14）。S2这个pooling层是对C1中的2*2区域内的像素求和乘以一个权值系数再加上一个偏置，然后将这个结果再做一次映射。

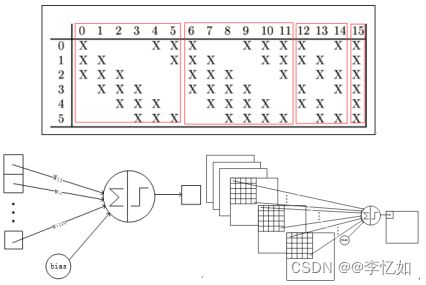
3、C3层： 参数：num_kernels=16, kernel_size=5×5, padding=0, stride=1 然后进行第二次卷积，输出是16个10x10的特征图. 我们知道S2 有6个 14*14 的特征图，这里是通过对S2 的特征图特殊组合计算得到的16个特征图。

4、S4层： 参数：kernel_size=2×2, padding=0, stride=2      处理和连接过程与S2类似，得到16个5x5的特征图。

5、C5/F5层： 参数：num_kernels=120，kernel_size=5×5, padding=0, stride=1，out_features=120 C5层是一个卷积层（实际上可以理解为全连接层）。由于S4层的16个图的大小为5x5，与卷积核的大小相同，所以卷积后形成的图的大小为1x1。形成120个卷积结果。

6、F6层： 参数：out_features=84     计算方法：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。 F6层有84个节点，对应于一个7x12的比特图，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应于一个ASCII编码。

7、F7层： 参数：out_features=10 Output层（F7层）共有10个节点，分别代表数字（类别）0到9，且如果节点i的值为0，则网络识别的结果是数字i。采用的是径向基函数（RBF）的网络连接方式，即为其损失函数。假设x是上一层的输入，y是RBF的输出，RBF输出的计算方式如式2： 式2 RBF输出计算方式 补充：原论文中的损失函数采用MSE，并添加了一个惩罚项，计算公式如式3： 式3 MSE + 惩罚项损失函数

至此，LeNet-5的核心网络解析完成，根据图表3与网络结构我们将手写数字识别过程深化到各层，如图7所示：

图7 基于LeNet-5的手写数字识别过程拆解

2.LeNet实现

2.1 代码实现与解析

上一节对LeNet的背景、发展、网络进行了深入剖析，本节根据原理在代码层面进行实现，并检测在分类数据集上的效果。

    Tips：由于算法年代比较久远且意义重大，故LeNet代码在网上有各种不同实现，但未必是对论文的完全还原（大部分是基于后续的tricks进行了优化），在此贴出一类优秀、简洁的代码实现（去掉了最后的高斯激活，其余与论文保持一致），来自李沐老师：6.6.卷积神经网络（LeNet） — 动手学深度学习 2.0.0 documentation (d2l.ai)。

在卷积神经网络的实现上，核心是网络的定义，根据LeNet-5的原理与各层参数，代码实现（Pytorch版）如下：

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                X = X.to(device)
            y = y.to(device)
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    timer, num_batches = d2l.Timer(), len(train_iter)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()
        for i, (X, y) in enumerate(train_iter):
            timer.start()
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l.plt.show()

 分析：根据Code我们可以看到代码实现与1中LeNet的论文网络定义保持一致，其中Conv2D为卷积层，AvgPool2D为平均池化（pooling）层，Dense为全连接层。每层输入参数与图表3/论文均保持一致。

而LeNet用于手写数字识别或其他分类任务时与实验1提到的ML/DL一般流程保持一致，即网络定义->数据导入与处理->模型训练->模型评估。

2.2 代码测试

在2.1根据原理编写好LeNet-5代码后，在本部分对其的原始分类效果进行测试，测试数据集为MNIST和Fashion-MNIST。

数据集可选择自己下载导入或使用代码导入，如Code2，代码导入样例如图8：

Code2 MNIST和Fashion-MNIST代码导入

from d2l import xx(框架) as d2l # Fashion-MNIST train_data, test_data = d2l.load_data_fashion_mnist(batch_size) # MNIST  train_dataset = datasets.MNIST(         root=r'./mnist', #此处为自己定义的下载存在目录         train=True,         download=True,         transform=transform #自定义转换方式)

图8 代码导入数据集样例

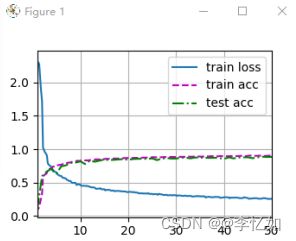
在数据集准备好后，输入网络进行训练和评估即可，本实验中的训练样例与结果样例如图9、图10所示：

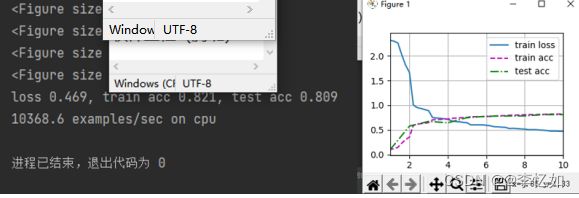
图9 LeNet训练过程样例

 图10 LeNet测试结果样例（Fashion-MNIST）

分析：根据图10，我们可以看到在Fashion-MNIST数据集上使用LeNet网络的train loss为0.469，train acc为0.821，test acc为0.809，同时验证了代码编写的正确性。

Tips：由于在MNIST数据集上acc达到98%+，故后续优化的效果比较不明显，后续优化对比测试均基于Fashion-MNIST。

3.LeNet优化

在上一节我们实现了与论文网络结构保持一致的LeNet，并通过两个数据集上的分类测试验证了代码的正确性，但在Fashion-MNIST的分类准确率只有80%左右（epoch=10，lr=0.9为例），仍有优化的空间，故本节以LeNet为例来探究深度模型优化的范式。

3.1 超参数

    深度学习很重要的一步是“调参”，而这个参数，一般指模型的超参数。重要/常见参超数总结如表2所示：

表2 重要/常见超参数总结

1、损失函数： 损失可以衡量模型的预测值和真实值的不一致性，由一个非负实值函数损失函数定义

2、优化器： 为使损失最小，定义loss后可根据不同优化方式定义对应的优化器

3、epoch： 学习回合数，表示整个训练过程要遍历多少次训练集

4、学习率： 学习率描述了权重参数每次训练之后以多大的幅度（step）沿梯下降的方向移动

5、归一化：     在训练神经神经网络中通常需要对原始数据进行归一化，以提高网络的性能

6、Batchsize： 每次计算损失loss使用的训练数据数量

7、网络超参数：     包括输入图像的大小，各层的超参数（卷积核数、尺寸、步长，池化尺寸、步长、方法，激活函数等）

3.2 优化与消融实验

Tips：所有单次的消融实验均不做网络架构的改变，对比的样例均（Batch_size=256，lr=0.9，epoch=10），并不做叠加处理对比，便于数据分析与结论的提出。

在进入优化与消融实验前，我们首先根据表2定义与过往实践对LeNet中待优化的超参数进行解析，并对效果做一定预测。

1. lr、Batch_size通过影响梯度影响效果（得确保在合适区间），同时影响模型收敛速度。
2. 效果一般会随着Epoch的增大先增大后稳定。
3. 网络超参数、损失函数、优化器等的不同选择一般对效果有较大影响，需要人为确定。

下面正式开始消融实验，尝试对经典LeNet进行优化。

Ⅰ、lr/Batch_size

第一Part我们首先分别对lr与Batch_size进行改变，并进行对比实验。

首先是lr，本实验从0-1.7，step=0.1，每个lr进行10次实验取平均值，部分数据汇总于表3（详见excel），lr对LeNet效果的影响如图11：

表3 lr对LeNet的效果影响数据汇总（部分）

lr	0.9	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7
loss	0.469	0.459	0.444	0.425	0.411	0.423	0.438	0.446	0.461
tr_acc	0.821	0.827	0.835	0.843	0.847	0.842	0.835	0.822	0.81
te_acc	0.809	0.828	0.766	0.83	0.825	0.831	0.772	0.764	0.758

图11 lr对LeNet效果的影响

分析：根据lr的消融实验我们可以发现LeNet的acc随lr的增长不断上升（一定波动），最后波动下降，本实验中较好的lr为1.2-1.4，而非0.9，test_acc可从0.809上升至0.83。

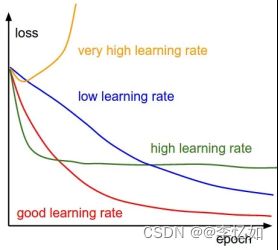
再泛化一点讲，学习率对模型影响是存在范式的，如图12所示（图源cs231n）：

图12 lr对模型的一般影响

实际上在LeNet中写死lr（lr不变）的做法是不合适的，在速度和效果上均不是最优选择（受限于当时的技术发展），在此对学习率的选择做简单补充。

首先我们要知道LeNet中使用的（优化器）是经典SGD算法，目前可以使用Adagrad，Adam等为代表的自适应学习策略优化器，如Code3，同样可以针对SGD进行精细调优，一般可以得到更好的效果。

Code3 优化器学习率改进

#经典SGD optimizer = torch.optim.SGD(net.parameters(), lr=lr) #自适应学习优化器 torch.optim.Adagrad(params, lr=lr, lr_decay=0, weight_decay=0, initial_accumulator_value=0)

然后是Batch_size,本实验从2-1024，取值均为2的幂，每个Batch_size进行10次实验取平均值，数据汇总于表4，Batch_size对LeNet效果的影响如图13：

表4 Batch_size对LeNet的效果影响数据汇总

batch_size	2	4	8	16	32	64	128	256	512	1024
loss	0.54	0.316	0.27	0.269	0.306	0.329	0.376	0.469	0.599	0.916
train_acc	0.811	0.882	0.898	0.9	0.885	0.878	0.861	0.821	0.767	0.637
test_acc	0.82	0.862	0.887	0.888	0.861	0.869	0.856	0.809	0.737	0.618

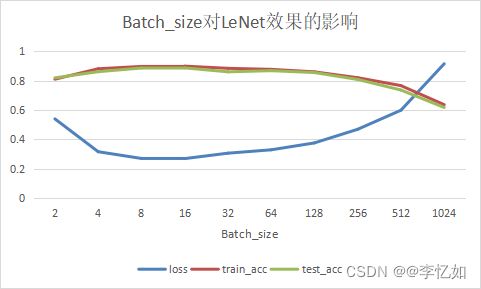
图13 Batch_size对LeNet效果的影响

分析：根据Batch_size的笑容实验我们可以发现LeNet的acc随Batch_size的增长不断上升再下降（但Batch_size小的时候收敛速度大大降低），本实验中较好的Batch_size为8或16，而非256，test_acc可从0.809上升至0.888。

而在现实情况中，一般不会单独考虑/改变lr或Batch_size,两者是有很强联系的。所以目前深度学习模型多采用批量随机梯度下降算法进行优化，原理如式4：

式4 批量随机梯度下降算法原理

n是批量大小(batch_size)，η是学习率(lr)。可知道除了梯度本身，这两个因子直接决定了模型的权重更新，从优化本身来看它们是影响模型性能收敛最重要参数。

学习率直接影响模型的收敛状态，batchsize则影响模型的泛化性能，两者又是分子分母的直接关系，相互也可影响。

Ⅱ、epoch

第二Part我们对epoch进行改变，并进行对比实验。

Tips：由于d2l.plt.show()与animator.show()可以静态/动态输出LeNet效果与epoch的关系，故直接使用其图进行数据分析。

本实验epoch取值区间为从0-100（测点为10、50、100），epoch对LeNet效果的影响如图10、14、15：

 

图14 测点epoch为50时LeNet的变化趋势

 图15 测点epoch为100时LeNet的变化趋势

分析：根据epoch的消融实验我们可以发现LeNet的acc随epoch的增长先上升后稳定（模型收敛），本实验中较好的epoch为50左右，而非10，test_acc可从0.809上升至0.89。

    Tips：epoch带来的模型优化是基于时间和算力资源的，真实情况下需做权衡。

Ⅲ、激活函数/池化方式

我们知道网络参数中卷积类型、池化方式、激活函数等选择都会影响模型效果，故第三Part我们对激活函数和池化方式进行改变，并进行对比实验。

根据图表3我们知道LeNet-5的激活函数为Sigmoid，池化方式为平均池化。

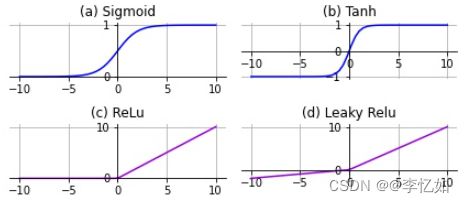
首先我们改变激活函数为目前主流的Relu（当时并没有），代码如Code4，不同激活函数的定义对比如图16，激活函数改变后进行10次实验取平均数据，对LeNet效果影响如图17，数据汇总于表5：

Code4 激活函数改变

#sigmoid nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid() #Relu nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU()

Tips：不要修改F6层的Sigmoid，尽量只对卷积层的激活函数操作。

图16 常用激活函数定义对比

表5 激活函数改变前后对LeNet的效果影响数据汇总

	Sigmoid	Relu
loss	0.469	0.28
train_acc	0.821	0.894
test_acc	0.809	0.884

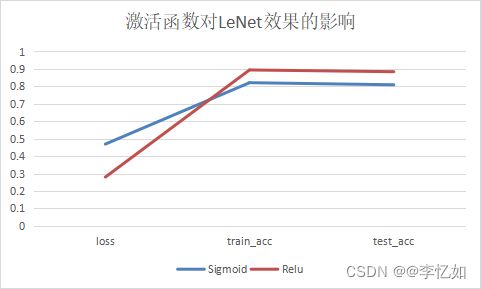
图17 激活函数改变对LeNet的影响

分析：根据图17与表5，我们发现卷积层的激活函数从Sigmoid改成Relu后LeNet的acc从0.809上升至0.884，验证了Relu的优化能力（更优激活函数）。

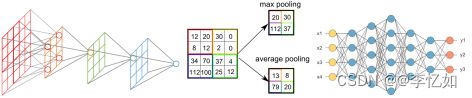
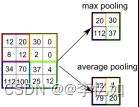
然后我们再将池化方式改为目前主流的最大池化（当时并没有），代码如Code5，定义如图18，池化方式改变后进行10次实验取平均数据，对LeNet效果影响如图19，数据汇总于表6：

图18 平均池化和最大池化的定义

Code5 池化方式改变

#平均池化 nn.AvgPool2d(kernel_size=2, stride=2) #最大池化 nn.MaxPool2d(kernel_size=2, stride=2)

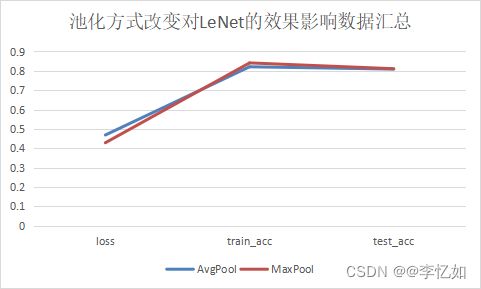
表6 池化方式改变前后对LeNet的效果影响数据汇总

	AvgPool	MaxPool
loss	0.469	0.429
train_acc	0.821	0.841
test_acc	0.809	0.811

图19 池化方式改变对LeNet的影响

分析：根据图19与表6，我们发现池化方式从平均池化改成最大池化后LeNet的指标均相对稳定，故本实验两种池化方式均可，当然有时间的情况下可以继续测试混合池化、随机池化等方法，在此不做展开。

Ⅳ、网络超参数

    第四Part我们针对网络超参数中带数量的参数（卷积与池化层的kernel_size、stride等）进行更改与对比实验，以Kernel_size为例。

    首先是卷积层的Kernel_size，默认为5，本实验从图像适配性上出发（Kernel_size范围合适）探究Kernel_size的变化对LeNet的影响，选取Cov2D（C1层）的Kernel_size为3-5，每个Kernel_size进行10次实验取平均值，数据汇总于表7，Kernel_size对LeNet效果的影响如图20：

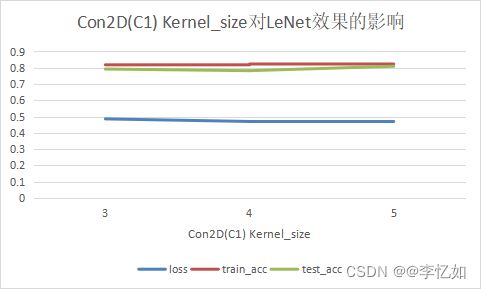
表7 Cov2D Kernel_size对LeNet的效果影响数据汇总

Cov Kernel_size	3	4	5
loss	0.486	0.47	0.469
train_acc	0.818	0.823	0.821
test_acc	0.792	0.782	0.809

图20 Cov2D Kernel_size对LeNet的效果影响

分析：根据Cov2D Kernel_size的消融实验我们可以发现LeNet的acc随Kernel_size的增长不断上升，故本实验中较好的Cov2D的Kernel_size为5。

然后我们改变Pooling_size，从2->1，改变后进行10次实验取平均数据，对LeNet效果影响数据汇总于表8：

表8 Pooling_size改变前后对LeNet的效果影响数据汇总

Pooling_size	1	2
loss	0.435	0.469
train_acc	0.84	0.821
test_acc	0.791	0.809

分析：根据表8，我们发现Pooling_size从2变为1后acc下降，loss增大，故本实验中较优Pooling_size仍为论文给出的2。

Ⅴ、最优参数组合

    根据前四Part测试出的最优参数，进行组合检测优化效果，本实验的最优参数（只列举测试过变化的参数）总结于表9，利用表9的参数组合在Fashion-MNIST进行十次实验取数据平均值，与论文/实验默认参数进行效果对比，数据汇总于表10，效果对比如图21：

表9 LeNet在Fashion-MNIST上的最优参数组合（实验自测）

参数	最优选择
Lr	1.2-1.4
Batch_size	8或16
Epoch	50左右即可
激活函数	ReLU
池化方法	AvgPool或MaxPool
Kernel_size（Cov）	5
Pooling_size	2

Tips：不同模型/算法没有固定的最优参数，且多个最优参数的组合未必是最优参数组合，本组合仅做优化效果验证，真实项目中得进行更精细的调参。

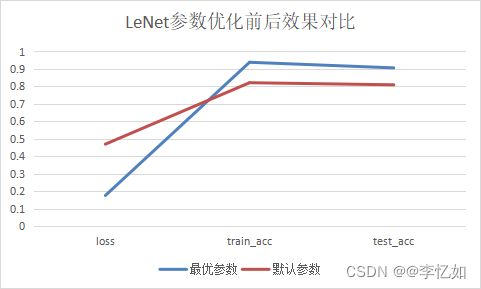
表10 参数优化前后对LeNet的效果影响数据汇总

	最优参数	默认参数
loss	0.175	0.469
train_acc	0.938	0.821
test_acc	0.906	0.809

图21 参数优化前后对LeNet的效果影响

分析：根据表10与图21，我们发现参数优化后LeNet在Fashion-MNIST的test_acc从0.809上升至0.906，验证了参数优化的效果。

四、高级架构介绍与选择实现

在上一章中我们深度解析了最经典CNN——LeNet的背景、网络架构，进行了在MNIST和Fashion-MNIST数据集上的测试，并通过不同超参数的消融实验介绍了深度模型中的超参数，并得到了一组较优参数组合，优化了模型效果。

但技术不断发展，太过古早的模型即使通过各种精细优化也很难与目前主流的卷积神经网络相提并论，故我们在本章根据图3选取LeNet之后的一些高级架构介绍并选取一种进行实验并进行性能对比。

1.AlexNet

参考论文：AlexNet.pdf    

LeNet的出现是爆炸性的，在MNIST数据集上的表现十分优秀，但很遗憾由于其在更大、更真实的数据集上的性能难以与当时的其他类模型（如SVM）比较，而在AlexNet出现后，CNN的时代才可谓正式来临。

1. 背景：AlexNet以很大的优势赢得了2012年ImageNet图像识别挑战赛（训练集包含120万张图片，验证集包含5万张图片，测试集包含15万张图片，这些图片分为了1000个类别，并且有多种不同的分辨率）。

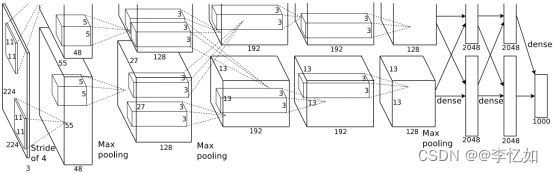
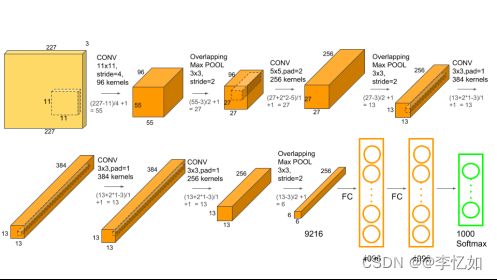
接下来我们来讲讲AlexNet的原理（网络设计），AlexNet是一个八层深度卷积神经网络，论文作者使用双GPU训练，网络架构与细节如图22与图23。但实际上AlexNet与LeNet设计是很相似的，主要区别如下：

1. AlexNet比相对较小的LeNet5要深得多。AlexNet由八层组成：五个卷积层、两个全连接隐藏层和一个全连接输出层。
2. AlexNet使用ReLU而不是sigmoid作为其激活函数。

图22 AlexNet网络架构（论文）

图23 AlexNet网络架构（细化） 

综述：AlexNet相较LeNet进行了网络的深化，且使用了数据增强、ReLU、局部相应归一化、Dropout、重叠池化、双GPU训练、端到端训练等方法提升模型效果与性能，在此不做展开。

2.VGG

参考论文：Very Deep Convolutional Networks for Large-Scale Image Recognition)

    虽然AlexNet证明深层神经网络卓有成效，但它没有提供一个通用的模板来指导后续的研究人员设计新的网络，直到2014年牛津大学团队提出了使用块的网络——VGG，其通过使用循环和子程序，可以很容易地在任何现代深度学习框架的代码中实现这些重复的架构。

经典卷积神经网络的基本组成部分是下面的这个序列：

①带填充以保持分辨率的卷积层

②非线性激活函数，如ReLU

③池化（Pooling）层，如最大池化

而一个VGG块与之类似，由一系列卷积层组成，后面再加上用于空间下采样的最大汇聚层。在最初的VGG论文中 (Simonyan and Zisserman, 2014)，作者使用了带有3x3卷积核、填充为1（保持高度和宽度）的卷积层，和带有2x2池化窗口、步幅为2（每个块后的分辨率减半）的最大汇聚层。

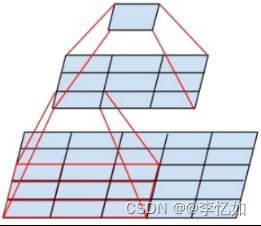
故VGG相比AlexNet的一个改进是采用连续的几个3x3的卷积核代替AlexNet中的较大卷积核（11x11，7x7，5x5），原理如图24所示。对于给定的感受野，采用堆积的小卷积核更优，因为多层非线性层可以增加网络深度以较小代价来保证学习更复杂的模式。

图24 卷积核替代原理

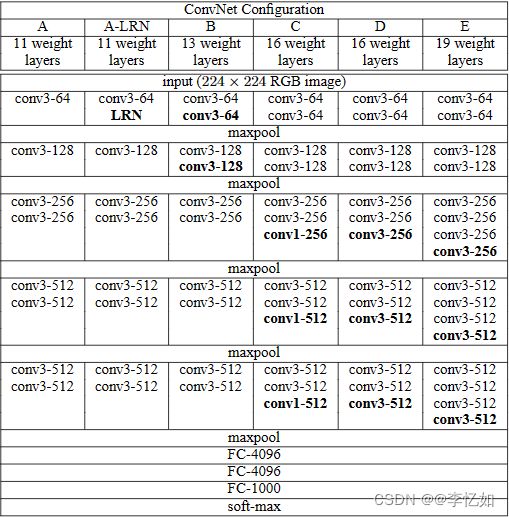
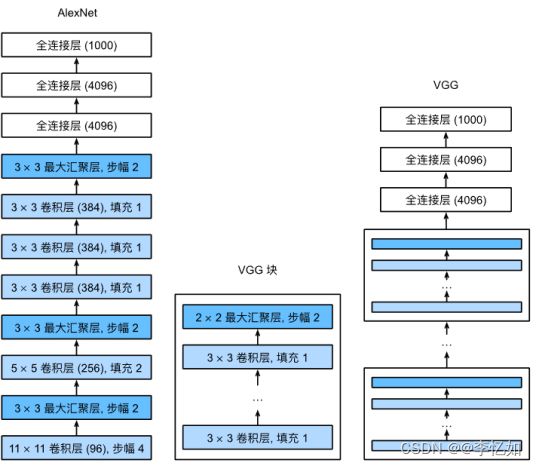
然后让我们回到VGG的网络设计，与AlexNet、LeNet一样，VGG网络可以分为两部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成，只不过使用了块设计实现，详细架构如图25所示，对比架构如图26所示：

图25 VGG网络架构 

图26 VGG vs AlexNet

综述：VGG主要是提出了块的概念，方便了后人进行CNN的设计与实现，同时VGG使用可复用的卷积块构造网络，非常高效的同时网络定义非常简洁。

3.NiN

参考论文：Network In Network.pdf (endnote.com)

LeNet、AlexNet和VGG都有一个共同的设计模式：通过一系列的卷积层与汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。然而，如果使用了全连接层，可能会完全放弃表征的空间结构。新国立团队提出的NiN提供了一个非常简单的解决方案。

NiN的两个主要创新如下：

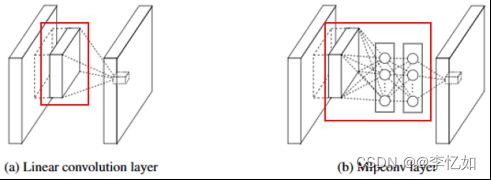
Ⅰ、将简单线性卷积层替换为多层感知机：如图27,多层感知机为多层全连接层和非线性函数的组合，提供了网络层间映射的一种新可能，同时增加了网络卷积层的非线性能力。

图27 NiN卷积层替换

Ⅱ、全连接层替换为全局池化层：如图28，假设分类任务共有C个类别。先前CNN中最后一层为特征图层数共计N的全连接层，要映射到C个类别上；改为全局池化层后，最后一层为特征图层数共计C的全局池化层，恰好对应分类任务的C个类别，这样一来，就会有更好的可解释性，且减少过拟合。

图28 NiN全连接层替换

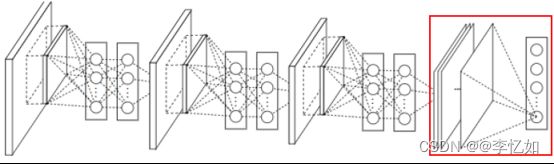
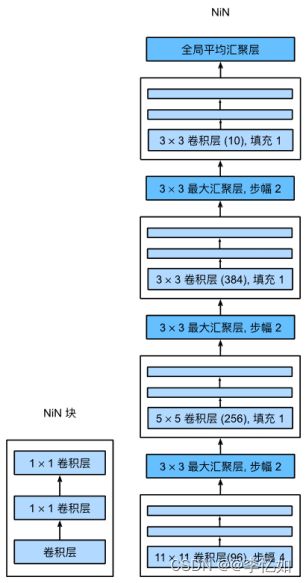
回到网络设计，NiN的网络架构如图29所示：

图29 NiN网络架构

4.ResNet

参考论文：[1512.03385] Deep Residual Learning for Image Recognition (arxiv.org)

    在AlexNet之后，大多研究者不断加深神经网络的深度以求得到更好的效果，但背后的数学验证与理论仍待论证。残差神经网络（ResNet）的主要贡献是发现了“退化现象（Degradation）”，并针对退化现象发明了 “快捷连接（Shortcut connection）”，极大的消除了深度过大的神经网络训练困难问题。

1. 退化现象：通过实验，ResNet随着网络层不断的加深，模型的准确率先是不断的提高，达到最大值（准确率饱和），然后随着网络深度的继续增加，模型准确率毫无征兆的出现大幅度的降低。ResNet团队把退化现象归因为深层神经网络难以实现“恒等变换（y=x）”，原因是由于非线性转换的加入。故提出了快捷连接分支，在线性转换和非线性转换之间寻求一个平衡。
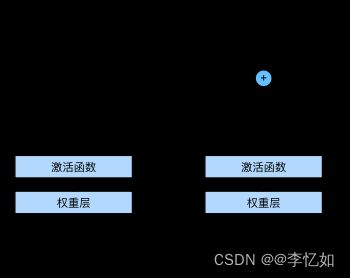
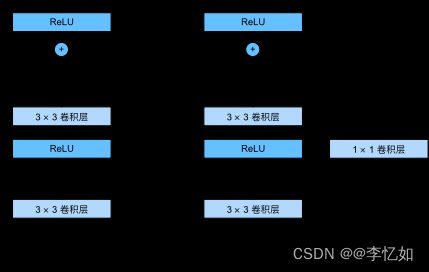
2. 快捷连接与残差块：残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一，这就是残差块的核心（带快捷连接），如图30所示：

图30 正常块 vs 残差块

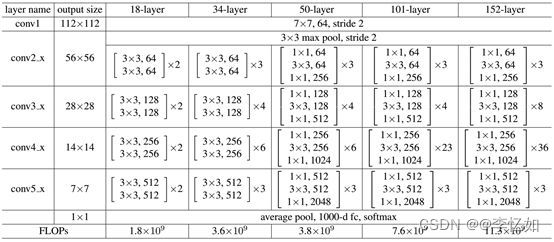
ResNet网络有各种网络，常见架构总结于图31：

图31 ResNet常用网络架构

综述：总的来说，ResNet利用残差映射可以更容易地学习同一函数，并利用残差块训练出一个有效的深层神经网络，为后续设计提供思路。

5.ResNet的实践

在上面的四节中我们对LeNet之后的高级CNN架构做了介绍，在本节我们以ResNet为例进行高级架构的实践，并与LeNet进行性能的对比。

根据第4节对ResNet的解析，我们知道它网络的实现实际上是残差块的堆叠，根据图30及其定义编写代码（Pytorch版）如下：

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Residual(nn.Module):  # @save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)


blk = Residual(3, 3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape
blk = Residual(3, 6, use_1x1conv=True, strides=2)
blk(X).shape
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))


def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk


b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)


lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l.plt.show()

补充：如图32所示，Residual代码生成两种类型的网络： 一种是当use_1x1conv=False时，应用ReLU非线性函数之前，将输入添加到输出。 另一种是当use_1x1conv=True时，添加通过1x1卷积调整通道和分辨率。

图32 残差块延申的两种网络选择

    Tips:每个模块有4个卷积层（不包括恒等映射的卷积层）。 加上第一个卷积层和最后一个全连接层，共有18层。 因此，这种模型通常被称为ResNet-18。

根据ResNet原理与Code6实现ResNet-18，并在与LeNet同样参数（epoch=10，lr=0.9，batch_size=256）的情况下同样在Fashion-MNIST上进行分类测试，实验进行10次取数据平均值，效果样例如图33，与LeNet的对比数据汇总于表11，对比效果如图34：

图33 ResNet在Fashion-MNIST上的分类效果样例

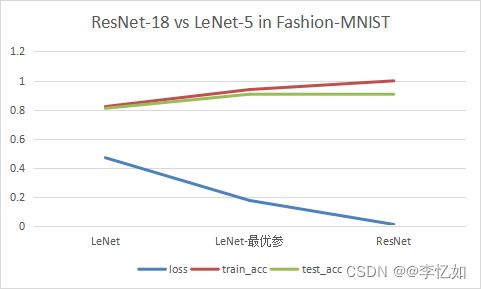
表11 ResNet-18 vs LeNet-5 in Fashion-MNIST

	LeNet	LeNet-最优参	ResNet
loss	0.469	0.175	0.01
train_acc	0.821	0.938	0.998
test_acc	0.809	0.906	0.902

图34 ResNet与LeNet性能对比

分析：如图34与表11所示，ResNet-18相较同参数LeNet-5在Fashion-MNIST上loss从0.469降为0.01，test_acc从0.809升为0.902，与最优参数组合LeNet效果相似。但由图33我们发现ResNet（原始，未优化）由于其较深的网络，在速度上远低于LeNet。

    Tips：对于ResNet同样可以采用对不同超参数的消融实验去寻找最优参数/组合优化效果，与LeNet类似。同时也可以改变ResNet网络架构做尝试，在此不做展开。

五、图像显著性与可视化诊断

在第二与第三章中我们介绍了各种卷积神经网络，并从代码方面实践并比较了不同参数组合的LeNet-5与ResNet-18，但在CNN训练的过程（特征贡献与选择）方面实际上还是一个“黑盒”，故本章我们介绍一些可视化诊断的方法，来更直观地观察CNN模型诞生的过程。

1.图像显著性

视觉/图像显著性是指对于真实世界中的场景，人们会自动的识别出感兴趣区域，并对感兴趣的区域进行处理，忽略掉不感兴趣的区域。

图像的注意预测，也称视觉显著性检测。指通过智能算法模拟人的视觉系统特点，预测人类的视觉凝视点和眼动，提取图像中的显著区域(即人类感兴趣的区域)，是计算机视觉领域关键的图像分析技术。部分图像及其注意预测结果示例如图35所示：

图35 部分图像及其注意预测结果示例 

2.特征可视化

参考论文：CAM.pdf (arxiv.org)、Grad-CAM.pdf (arxiv.org)

根据本章梗概我们知道神经网络是一个“黑盒”，我们只知道输入和输出，但对于其中的特征选择、训练过程只停留在数理推论/证明层面，而特征可视化技术则是一种研究“深度模型可解释性”常见方法。

2.1 CAM

首先我们来讲讲该领域广义上的开山之作——CAM（Class Activation Mapping）。CAM即类别激活映射图，也被称为类别热力图、显著性图等。根据显著性定义，可以理解为对预测输出的贡献分布，分数越高的地方表示原始图片对应区域对网络的响应越高、贡献越大。

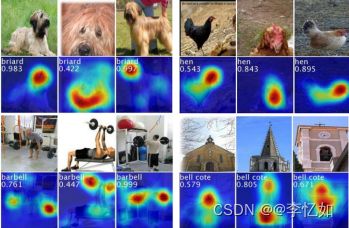
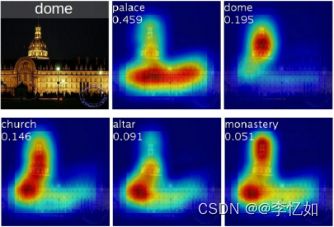
    可视化的时候，可以利用热力图和原图叠加的形式呈现。如图36，颜色越深红的地方表示值越大。可以认为，网络预测“狗”这个类别时，红色高亮区域是其主要判断依据。同理，一些CAM的其他样例可见图37：

图36 CAM预测“狗”的样例 

图37 CAM预测样例

而聊完CAM的定义，来讲讲它（特征可视化的作用），总结如表12：

表12 特征可视化作用

1、深度模型工作原理的深入理解： 特征可视化使模型中的特征贡献度更直观，流程更清晰，有助于理解和分析神经网络的工作原理及决策过程，且不同的模型对同样数据有不同的预测，故可以通过A/B测试进而更好地选择或设计网络。

2、可视化信息引导网络更好地学习： 例如可利用 CAM 信息通过"擦除"或"裁剪"的方式对数据进行增强。

3、协助弱监督语义分割或弱监督定位： 由于 CAM 能够覆盖到目标物体，因此仅利用分类标注也可用来完成语义分割或目标检测任务，这极大程度降低了标注的工作量。当然，对分类网络的 CAM 精度的要求很高，不然误差相对较大。

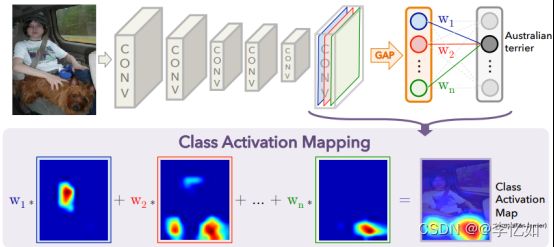
接下来我们来介绍CAM的原理，其网络结构如图38所示：

图38 CAM原理及网络结构

综述：如图38，这是一个基于分类训练的CNN网络，最左边是输入，中间是很多卷积层，在最后一层卷积层之后接的是全局平均池化层（GAP，把特征图转换成特征向量，详见VGG16），最后接一层softmax，得到输出。

补充：因为CAM基于分类，所以被激活的区域是根据分类决定的，即同一个特征图，只更新不同的权重，即使我们使用同一张input，如图39所示：

图39 CAM参数更新效果对比

根据CAM的原理，将获取CAM的流程如下：

·  1）提取需要可视化的特征图，例如尺寸为512*7*7的张量；

·  2）获取该张量的每个 channel 的权重，即长度为512的向量；

·  3）通过线性融合的方式，将该张量在 channel 维度上加权求和，获取尺寸为7*7的 map；

·  4）对该 map 进行归一化，并通过插值的方式 resize 成和原图一样的尺寸。

2.2 Grad-CAM

CAM是经典的特征可视化算法，但局限性是网络中必须有GAP层，泛化性能较差，部分结构的CNN可视化需要修改网络结构或者重新训练。故一个更通用的方法被提出——Grad-CAM，主要区别如下：

CAM 只能用于最后一层特征图和输出之间是GAP的操作，grad-CAM可适用非GAP连接的网络结构。

CAM只能提取最后一层特征图的热力图，而gard-CAM可以提取任意一层。

Grad-CAM解决CAM局限的核心思想是使用流入CNN的最后一个卷积层的梯度信息为每个神经元分配重要值，以进行特定的关注决策。网络架构如图40，样例如图41： 

图40 Gram-CAM网络架构

图41 Gram-CAM可视化样例

2.3 其他特征可视化

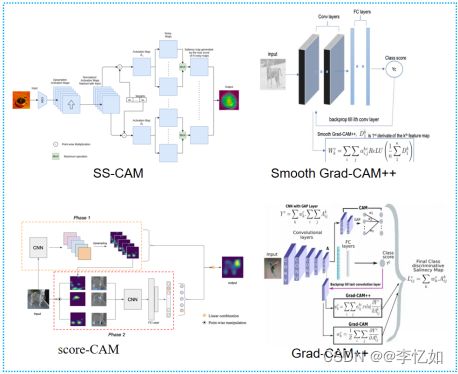
CAM与Grad-CAM是比较经典的特征可视化方法，在此之后又出现了Grad-CAM++、Smooth Grad-CAM++、score-CAM 和 ss-CAM等算法，架构如图42所示，在此不做展开。

图42 其他特征可视化网络架构

3.CAM可视化诊断实践

介绍完特征可视化的定义与各种方法的原理/架构，本节以CAM为例对上两章章提到的CNN进行可视化诊断。

根据CAM的定义与流程，核心为提取到特征图和目标类别全连接的权重，直接加权求和，再经过relu操作去除负值，最后归一化获取CAM，编写核心代码如Code7：

Code7 CAM核心代码

# 获取全连接层的权重 self._fc_weights = self.model._modules.get(fc_layer).weight.data # 获取目标类别的权重作为特征权重 weights=self._fc_weights[class_idx, :] # 这里self.hook_a为最后一层特征图的输出 batch_cams = (weights.unsqueeze(-1).unsqueeze(-1) * self.hook_a.squeeze(0)).sum(dim=0) # relu操作,去除负值 batch_cams = F.relu(batch_cams, inplace=True) # 归一化操作 batch_cams = self._normalize(batch_cams)

使用ResNet18、ResNet50、 DenseNet121的完整代码如下：

import numpy as np
from torchvision import models, transforms
import cv2
from PIL import Image
from torch.nn import functional as F

# 定义预训练模型: resnet18、resnet50、densenet121
resnet18 = models.resnet18(pretrained=True)
resnet50 = models.resnet50(pretrained=True)
densenet121 = models.densenet121(pretrained=True)
resnet18.eval()
resnet50.eval()
densenet121.eval()

# 图片数据转换
image_transform = transforms.Compose([
    # 将输入图片resize成统一尺寸
    transforms.Resize([224, 224]),
    # 将PIL Image或numpy.ndarray转换为tensor，并除255归一化到[0,1]之间
    transforms.ToTensor(),
    # 标准化处理-->转换为标准正太分布，使模型更容易收敛
    transforms.Normalize(
        mean=[0.485, 0.456, 0.406],
        std=[0.229, 0.224, 0.225]
    )
])

# =====注册hook start=====
feature_data = []


def feature_hook(model, input, output):
    feature_data.append(output.data.numpy())


resnet18._modules.get('layer4').register_forward_hook(feature_hook)
resnet50._modules.get('layer4').register_forward_hook(feature_hook)
densenet121._modules.get('features').register_forward_hook(feature_hook)
# =====注册hook end=====

# 获取fc层的权重
fc_weights_resnet18 = resnet18._modules.get('fc').weight.data.numpy()
fc_weights_resnet50 = resnet50._modules.get('fc').weight.data.numpy()
fc_weights_densenet121 = densenet121._modules.get('classifier').weight.data.numpy()

# 获取预测类别id
image = image_transform(Image.open("cat.jpg")).unsqueeze(0)
out_resnet18 = resnet18(image)
out_resnet50 = resnet50(image)
out_densenet121 = densenet121(image)
predict_classes_id_resnet18 = np.argmax(F.softmax(out_resnet18, dim=1).data.numpy())
predict_classes_id_resnet50 = np.argmax(F.softmax(out_resnet50, dim=1).data.numpy())
predict_classes_id_densenet121 = np.argmax(F.softmax(out_densenet121, dim=1).data.numpy())


# =====获取CAM start=====
def makeCAM(feature, weights, classes_id):
    print(feature.shape, weights.shape, classes_id)
    # batchsize, C, h, w
    bz, nc, h, w = feature.shape
    # (512,) @ (512, 7*7) = (49,)
    cam = weights[classes_id].dot(feature.reshape(nc, h * w))
    cam = cam.reshape(h, w)  # (7, 7)
    # 归一化到[0, 1]之间
    cam = (cam - cam.min()) / (cam.max() - cam.min())
    # 转换为0～255的灰度图
    cam_gray = np.uint8(255 * cam)
    # 最后，上采样操作，与网络输入的尺寸一致，并返回
    return cv2.resize(cam_gray, (224, 224))


cam_gray_resnet18 = makeCAM(feature_data[0], fc_weights_resnet18, predict_classes_id_resnet18)
cam_gray_resnet50 = makeCAM(feature_data[1], fc_weights_resnet50, predict_classes_id_resnet50)
cam_gray_densenet121 = makeCAM(feature_data[2], fc_weights_densenet121, predict_classes_id_densenet121)
# =====获取CAM start=====

# =====叠加CAM和原图，并保存图片=====
# 1)读取原图
src_image = cv2.imread("cat.jpg")
h, w, _ = src_image.shape
# 2)cam转换成与原图大小一致的彩色度(cv2.COLORMAP_HSV为彩色图的其中一种类型)
cam_color_resnet18 = cv2.applyColorMap(cv2.resize(cam_gray_resnet18, (w, h)),
                                       cv2.COLORMAP_HSV)
cam_color_resnet50 = cv2.applyColorMap(cv2.resize(cam_gray_resnet50, (w, h)),
                                       cv2.COLORMAP_HSV)
cam_color_densenet121 = cv2.applyColorMap(cv2.resize(cam_gray_densenet121, (w, h)),
                                          cv2.COLORMAP_HSV)
# 3)合并cam和原图，并保存
cam_resnet18 = src_image * 0.5 + cam_color_resnet18 * 0.5
cam_resnet50 = src_image * 0.5 + cam_color_resnet50 * 0.5
cam_densenet121 = src_image * 0.5 + cam_color_densenet121 * 0.5
cam_hstack = np.hstack((src_image, cam_resnet18, cam_resnet50, cam_densenet121))
cv2.imwrite("cam_hstack.jpg", cam_hstack)
# 可视化
Image.open("cam_hstack.jpg").show()

而上一部分也提到，对同样的分类任务/图像，不同模型会有不同的可视化结果，故本部分实验选取LeNet、ResNet18、ResNet50，获取方式为torch.models直接导入。定义好网络和编写好CAM代码后，使用不同种类的图片进行测试，结果如图43所示：

图43 可视化诊断测试效果

分析：如图43所示，左图利用CAM对LeNet分类MNIST做了可视化，使特征贡献更加直观。右图对个人自测图使用不同深度的ResNet，得到了不同的可视化诊断，符合预期。同时验证了CAM代码设计实现的正确性。

4.其他可视化诊断拓展

CAM、Grad-CAM等主要是通过特征可视化的方法来解释深度学习模型，而图像的显著性检测是更广义的可视化诊断，拓展可见：计算机视觉——图像视觉显著性检测_@李忆如的博客-CSDN博客

六、总结 

1.实验结论 

本次实验完成任务梳理如表16，不同CNN简介与对比如表17所示：

表16 实验2完成任务梳理

1、理论梳理：     第一章进行了卷积神经网络的综述（概念、原理、发展历程）与CNN训练的基本原理与流程介绍，在二三章中对按时间线各种高级CNN模型进行了原理与架构解析，并对不同可视化诊断算法（特征可视化、显著性检测等）的定义与流程进行了总结。

2、多种CNN实践与优化：     对LeNet-5的不同框架版本（Tensorflow、Pytorch）进行了实现，并在MNIST、Fashion-MNIST两个分类数据集上进行了实践，同时对各种超参数均进行了消融实验，并找到了一组较优参数对LeNet进行了较大优化。此外，选取ResNet作为高级CNN代表进行了实现，并与LeNet、最优参数LeNet进行了性能对比。

3、模型的可视化诊断：     利用CAM对LeNet分类MNIST的过程进行了可视化，并使用自定义数据集对比了ResNet18与ResNet50的可视化效果。

4、方案补充：     对于CNN的高级架构与可视化方案，除了给定的要求，均作了相关的拓展。

表17 不同CNN简介与对比

CNN	简介
LeNet	广义上CNN的开山之作，起源于手写数字识别任务，7层网络（卷->池->全连接）。
AlexNet	真正开启CNN的热潮，类似LeNet的八层网络，激活函数改为ReLU,加入数据增强、ReLU、局部相应归一化、Dropout、重叠池化、双GPU训练、端到端训练等方法优化。
VGG	提出了块网络的设计，使用循环和子程序，可以很容易地在任何现代深度学习框架的代码中实现这些重复的架构。
NiN	为解决全连接层带来的空间结构丢失，NiN将简单线性卷积层替换为多层感知机，同时将全连接层替换为全局池化层。
ResNet	为解决“退化现象”，ResNet使用带“残差块”的网络，利用残差映射可以更容易地学习同一函数，并利用残差块训练出一个有效的深层神经网络。

补充：无论是CNN的选择还是可视化诊断算法的选择，都需要和实际需求紧密结合，并不存在某种模型/算法适用于各种数据集、任务、算力资源中。

2. 参考资料

1.CV-Tech-Guide/Visualize-feature-maps-and-heatmap: 可视化特征图教程 (github.com)

2.MLND/Class Activation Map Visualizations.ipynb at master · mtyylx/MLND · GitHub

3.特征可视化技术——CAM - 简书 (jianshu.com)

4.报错：总结该问题解决方案：OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md 

5.LeNet：第一个卷积神经网络 (ruanx.net) 

6.细品经典：LeNet-1, LeNet-4, LeNet-5, Boosted LeNet-4_flyfor2013的博客-CSDN博客

7.LeNet详解_CharlesOAO的博客-CSDN博客

8.深度学习卷积神经网络-AlexNet - 知乎 (zhihu.com) 

9.动手学深度学习 2.0.0 documentation (d2l.ai) 

10.万字长文：特征可视化技术(CAM) - 知乎 (zhihu.com)