举重比赛按照运动员的体重分组，拟合体重与总成绩的关系(老师布置的作业)

非常小白，有问题有错误，各位大佬请指正！！！！

问题：

1.符号假设

$y$ 举重成绩

$t$ 力度

$s$ 肌肉横截面积

$q$ 特征尺寸

$w$ 体重

2.分析1

假设1

举重成绩与力度成正比，即$y\propto ty=k_{1}t$

力度与肌肉横截面积成正比， 即$t\propto st=k_{2}s$

肌肉横截面积与某种特征尺寸成正比， 即$s\propto qs=k_{3}q$

体重与某种特征尺寸成正比， 即$w\propto qw=k_{4}q$

将上面的公式结合得，$$y=\frac{k_1{k}_2{k}_{3}w}{k_4}$$

3.模型1求解

集合表中数据利用最小二乘法的思想，来求关系式$y=\frac{k_1{k}_2{k}_{3}w}{k_4}$的比例系数，利用python scipy库求解

程序，如下

from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
import numpy as np
from scipy.optimize import leastsq
def err(p, x, y):
    return p[0] * x  - y
p0 = [100]
Xi=np.array([54, 59, 64, 70, 76, 83, 91, 99, 108])
Yi=np.array([287.5, 307.5, 335, 357.5, 367.5, 392.5, 402.5, 420, 430])
ret = leastsq(err, p0, args = (Xi, Yi))
print (ret) 
import matplotlib.pyplot as plt
k = ret[0]
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3)
x = np.linspace(50,110,1000)
y = k * x 
plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2)
plt.xlabel("最大体重(y)/kg", fontsize=12)
plt.ylabel("总成绩(w)/kg", fontsize=12)
plt.legend()
plt.grid()
plt.show()  

结果：

由上图可以看出拟合度较差

猜测，用线性函数对举重成绩与体重进行拟合的模型过于简单

所以我们再次猜测

4.分析2

假设2

举重成绩与力度成正比，即$y\propto ty=k_{1}t$

力度与肌肉横截面积成正比， 即$t\propto st=k_{2}s$

肌肉横截面积与某种特征尺寸的平方成正比， 即$s\propto q^{2}s=k_3{q}^2$

体重与某种特征尺寸成正比， 即$w\propto qw=k_{4}q$

将上面的公式结合得，$$y=\frac{k_1{k}_2{k}_3{w}^2}{k_4}$$

5.模型2求解

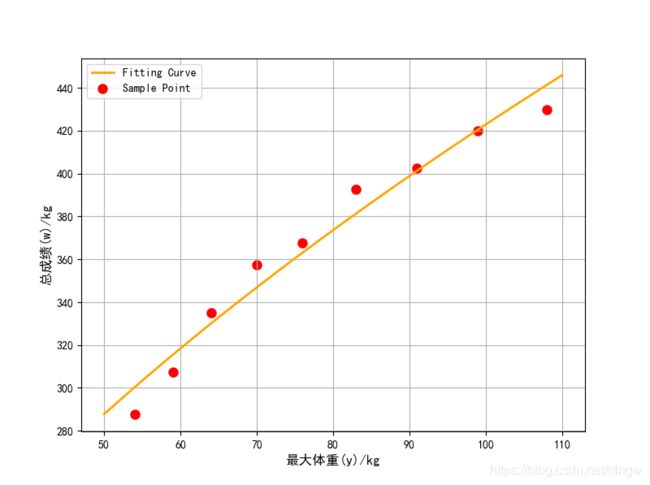
集合表中数据利用最小二乘法的思想，来求关系式$y=\frac{k_1{k}_2{k}_3{w}^2}{k_4}$的比例系数，利用python scipy库求解

即模型 $$y\propto k{w}^{\alpha }$$

程序，如下

from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
import numpy as np
from scipy.optimize import leastsq
Xi=np.array([54, 59, 64, 70, 76, 83, 91, 99, 108])
Yi=np.array([287.5, 307.5, 335, 357.5, 367.5, 392.5, 402.5, 420, 430])
def error(p,x,y):
    return p[0]*x**p[1]-y
p0 = [5,2]
ret = leastsq(error,p0,args=(Xi,Yi))
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3)
x = np.linspace(50,110,1000)
y = 32.74825487 * x ** 0.55553414
plt.plot(x,y,color="orange",label="Fitting Curve",linewidth=2)
plt.xlabel("最大体重(y)/kg", fontsize=12)
plt.ylabel("总成绩(w)/kg", fontsize=12)
plt.legend()
plt.grid()
plt.show()
from sympy import *
x = symbols('x')
e = 32.74825487 * x ** 0.55553414
print("函数:")
print(e)

结果：

函数:
32.74825487*x**0.55553414

从上图看出，模型2理论值与实际值非常接近
即求解