五、高级数据结构和算法：2-3查找树、红黑树
5 2-3查找树、红黑树
5.1 2-3查找树
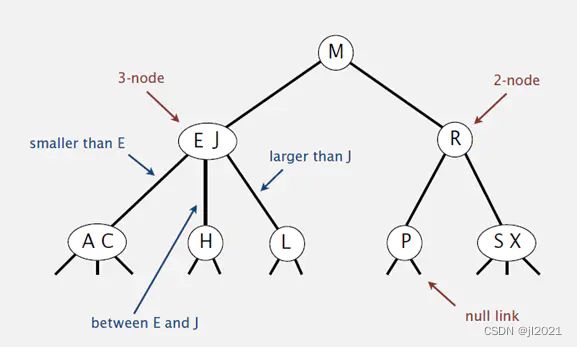
和二叉树不一样，2-3树每个节点保存1个或者2个的key。
对于普通的2节点(2-node)，要有1个key和左右两个子节点。
对应3节点(3-node)，要有两个Key和三个子节点。
2-3查找树的定义如下：
（1）要么为空，要么：
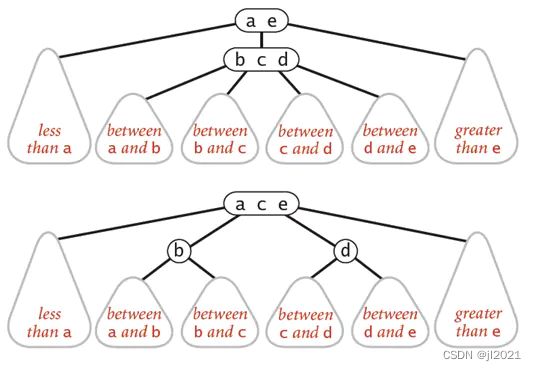
（2）对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key有效，有节点也是一个2-3节点，所有的值比key要大。
（3）对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。
5.1.2 操作
5.1.3 查找
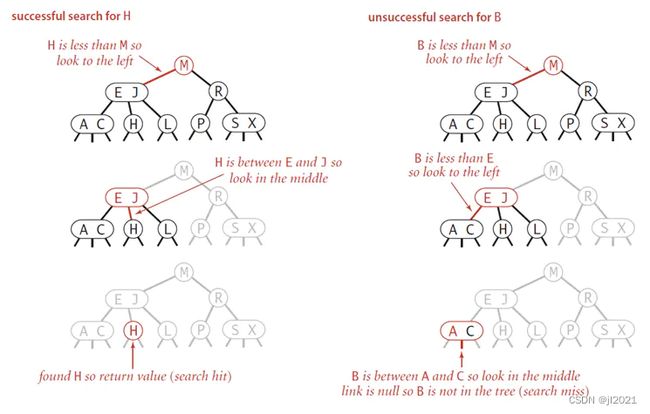
2-3树的查找和二叉查找树类似，要确定一个树是否属于2-3树，我们首先和其跟节点进行比较，如果相等，则查找成功；否则根据比较的条件，在其左中右子树中递归查找，如果找到的节点为空，则未找到，否则返回。
5.1.4 插入
- （1）往一个2-node节点插入
往2-3树中插入元素和BST插入元素一样，首先要进行查找，然后将节点挂到未找到的节点上。
如果查找后未找到的节点是一个2-node节点，只需要将新的元素放到这个2-node节点里面使其变成一个3-node节点即可。
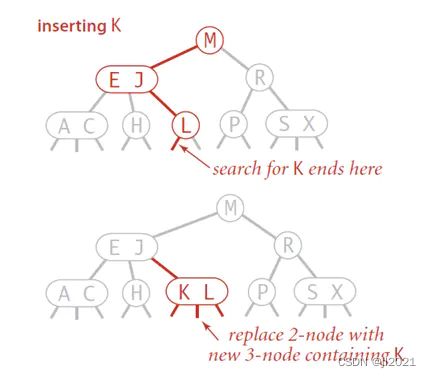
- （2）往一个3-node节点插入
往一个3-node节点插入一个新的节点可能会遇到很多种不同的情况。例如：
a）只包含一个3-node节点
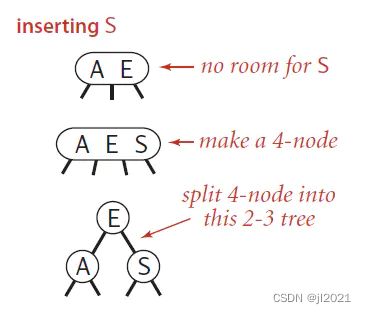
b）节点是3-node，父节点是2-node
和第一种情况一样，我们也可以将新的元素插入到3-node节点中，使其成为一个临时的4-node节点，然后，将该节点中的中间元素提升到父节点即2-node节点中，使其父节点成为一个3-node节点，然后将左右节点分别挂在这个3-node节点的恰当位置。
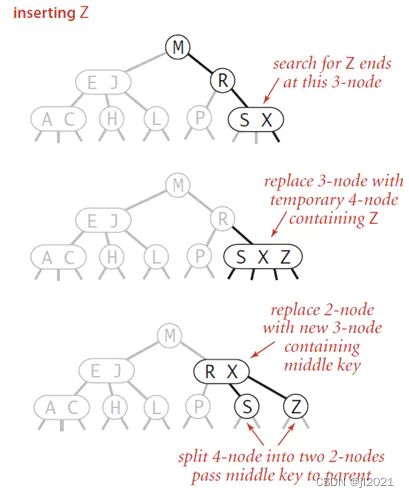
c）节点是3-node，父节点也是3-node
当插入的节点是3-node的时候，将该节点拆分，中间元素提升至父节点，但是此时父节点是一个3-node节点，插入之后，父节点变成了4-node节点，然后继续将中间元素提升至其父节点，直至遇到一个父节点是2-node节点，然后将其变为3-node，不需要继续进行拆分。
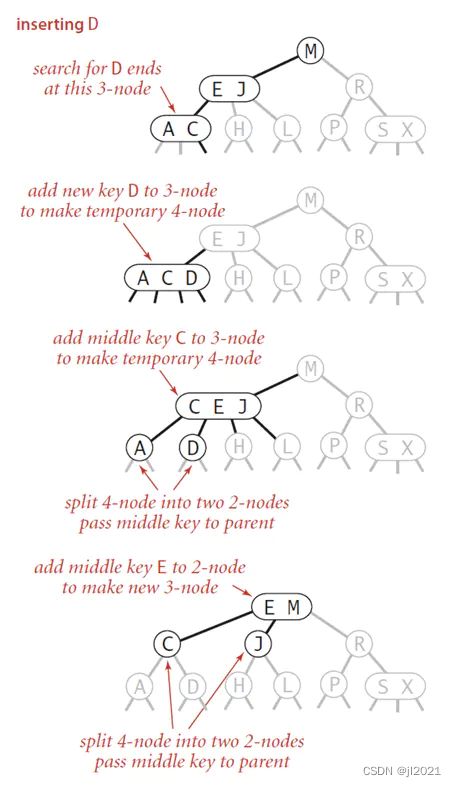
d）根节点分裂
当根节点到字节点都是3-node节点的时候，这是如果要在字节点插入新的元素的时候，会一直查分到跟节点，在最后一步的时候，跟节点变成了一个4-node节点，这个时候，就需要将跟节点查分为两个2-node节点，树的高度加1。
5.1.5 本地转换
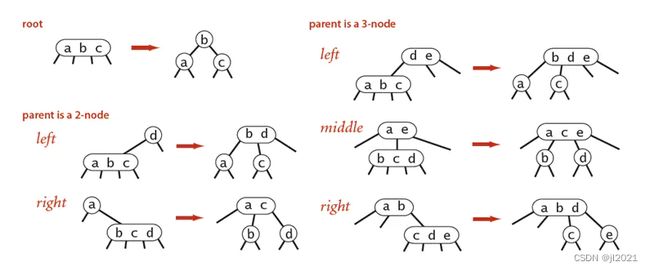
将一个4-node拆分为2-3node涉及到6种可能的操作。这4-node可能在跟节点，也可能是2-node的左子节点或者右子节点。或者是一个3-node的左，中，右子节点。所有的这些改变都是本地的，不需要检查或者修改其他部分的节点。所以只需要常数次操作即可完成2-3树的平衡。
注：2-3树之所以能够保证在最差的情况下的效率的原因在于其插入之后仍然能够保持平衡状态。
5.1.6 性质
这些本地操作保持了2-3树的平衡。对于4-node节点变形为2-3节点，变形前后树的高度没有发生变化。只有当跟节点是4-node节点，变形后树的高度才加一。
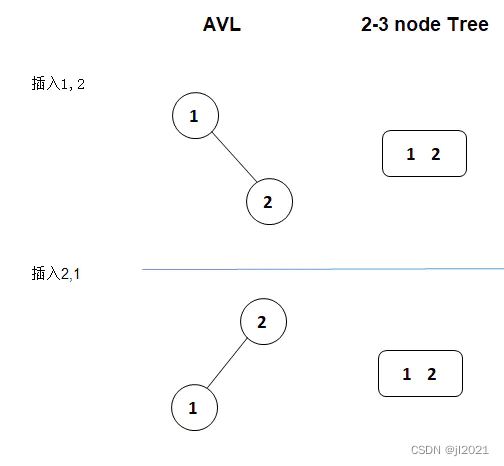
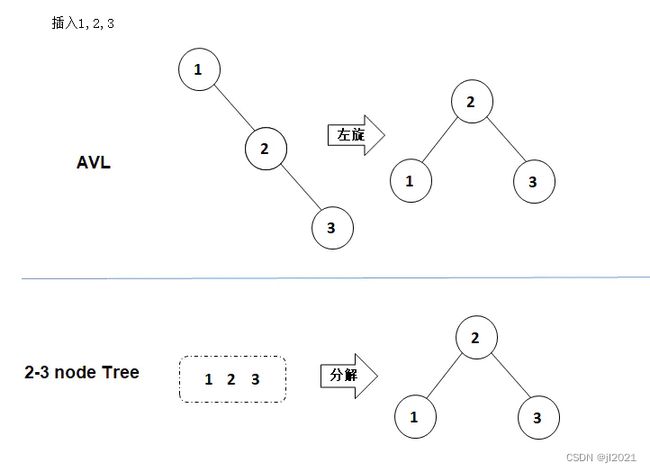
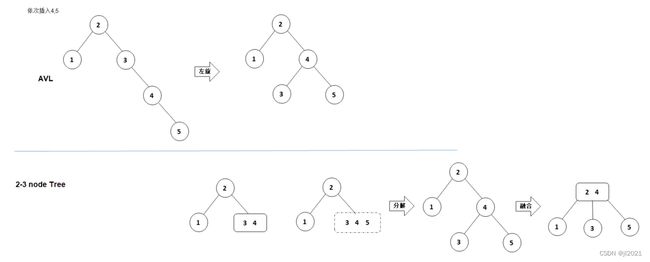
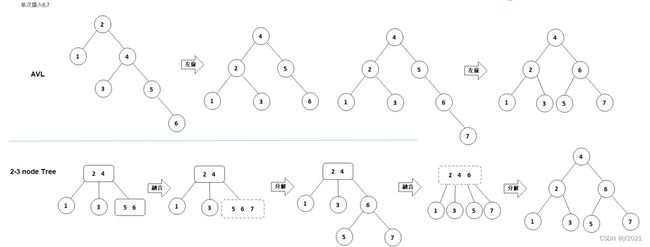
5.1.7 AVL树 vs. 2-3查找树
5.2 红黑树(Red-Black Tree)
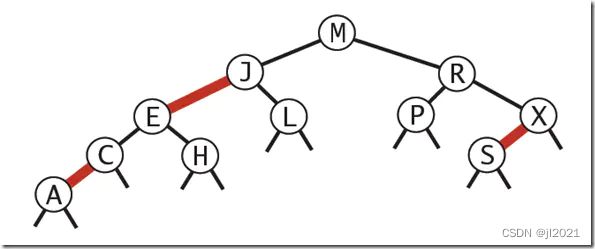
红黑树是一种具有红色和黑色链接的BST。
《算法导论》中对红黑树的定义（针对的是节点颜色，基于2-3-4数）：
（1）节点是红色或黑色树
（2）根节点和叶子节点（NIL节点）都是黑色。
（3）每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点，也就是没有5-node)
（4）从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。(黑色节点完美平衡)
《算法》中对红黑树的定义（针对的是线的颜色，基于2-3树）：
（1）红色的线永远是左侧链接。（强行的规定）
（2）没有一个节点同时链了两条红色的线。（也就是没有4-node）
（3）任何从根到叶子节点的路径上有相同颜色的黑线。(黑线节点完美平衡)
- 红黑树
5.2.1 背景
2-3查找树能保证在插入元素之后能保持树的平衡状态，最坏情况下即所有的子节点都是2-node，树的高度为lgN，从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂。红黑树是一种简单实现2-3树的数据结构。
-
红黑树平衡
-
红黑树转2-3树
本质：红黑树是对2-3查找树进行编码。
对2-3查找树中的3-nodes节点添加额外的信息。
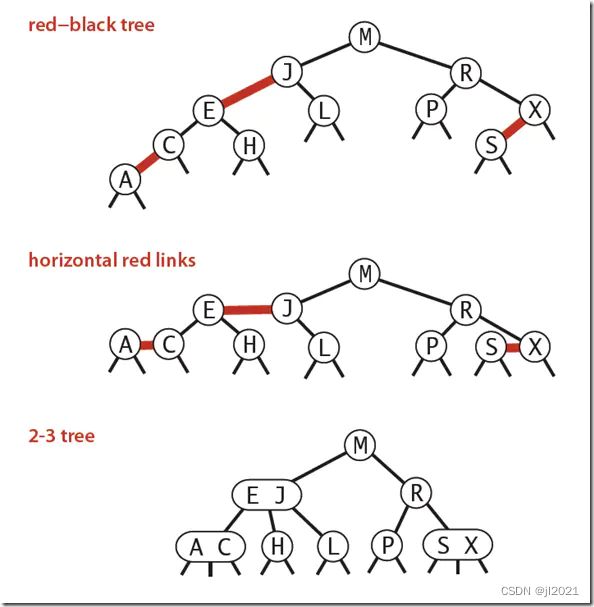
红黑树中将节点之间的链接分为两种不同类型。
红色链接：链接两个2-nodes节点来表示一个3-nodes节点。
黑色链接：链接普通的2-3节点。
从边的颜色到节点的颜色
BST的每一个节点上增加一个新的表示颜色的标记。该标记指示该节点指向其父节点的颜色。
5.2.2 操作
- 平衡化
与AVL相同，红黑树也需要通过旋转保持平衡；不同的是旋转后，需要改变节点的颜色。
5.2.3 旋转(Rotate)
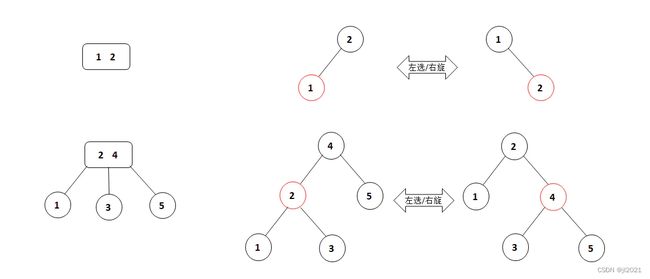
- 左旋
将一个向右倾斜的红色链接旋转为向左链接,将红线链接的两个节点中的一个较大的节点移动到根节点上。
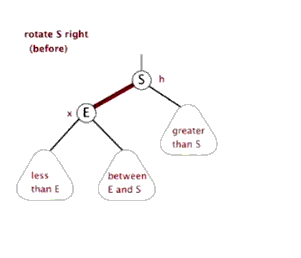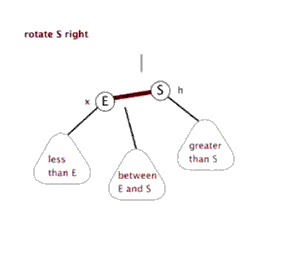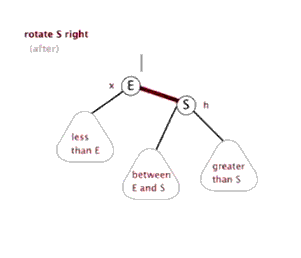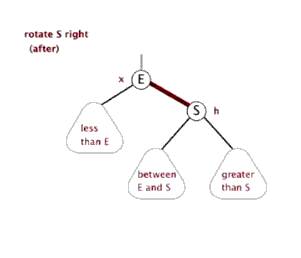
- 右旋
将一个向左倾斜的红色链接旋转为向右链接,将红线链接的两个节点中的一个较大的节点移动到根节点上。
-
暂时的旋转
旋转颜色变化规律：上升节点(旋转节点)变为原来父节点的颜色，下降节点变为红色。 -
AVL和红黑树旋转的比较
红黑树在AVL的基础上加入了颜色的变化
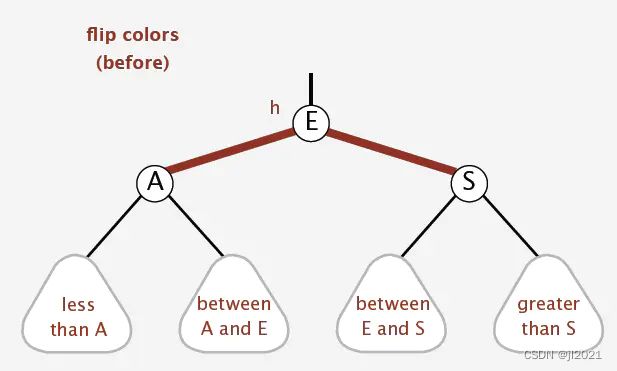
5.2.4 颜色反转(Color Flip)
当出现一个临时的4-node的时候，即一个节点的两个子节点均为红色。子节点颜色为黑色，父节点的颜色设置为红色；反之亦然。
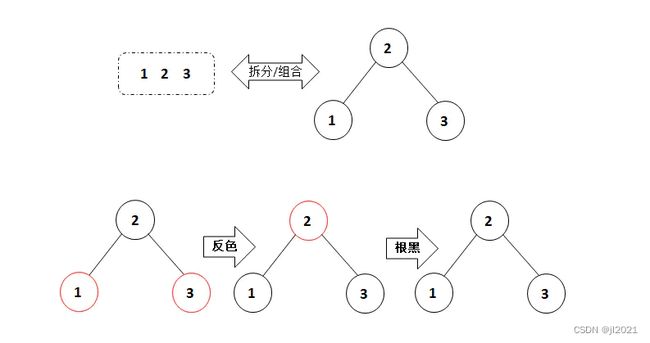
因为2是根节点，所以要根黑
二叉树中，根节点永远是黑色。
5.2.5 红节点转移(Move Red)
本质：红节点转移实质上形成一个5节点。
- 实例
#include 1--2
2--3[color=red]
1--3
3--2[color=red]
1--2
2--3[color=red]
5.2.6 插入
一切为了平衡，树根到叶子节点的路径上黑边的个数(黑节点个数)决定平衡。
从上到下查找位置，插入节点为红叶子节点，然后从下到上回溯平衡。
- 往一个2-node节点底部插入新的节点
（1）按照BST遍历，新插入的节点标记为红色。
为什么新插入节点是红色？为了保证插入后树是平衡的(每条分支黑边个数不发生改变)。
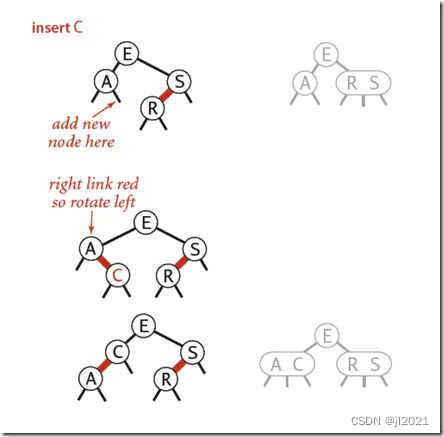
（2） 如果新插入的节点在父节点的右子节点，则需要进行左旋操作。
为什么要左旋？因为红色的线永远是左侧链接。
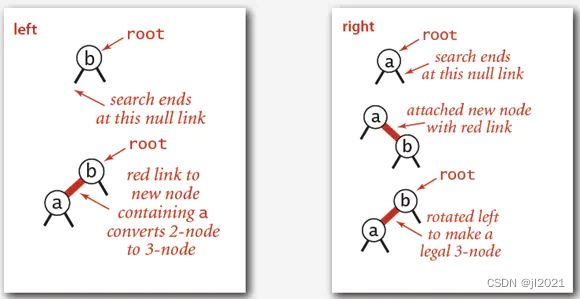
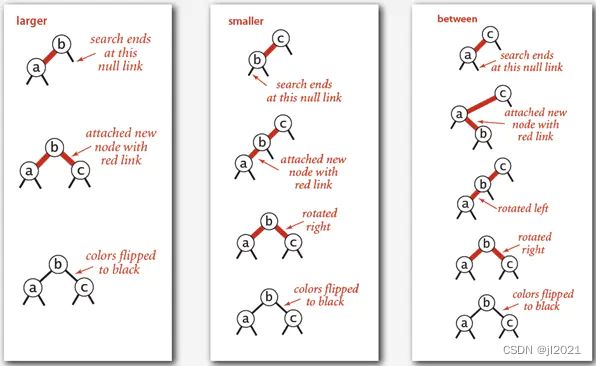
- 往一个3-node节点底部插入新的节点
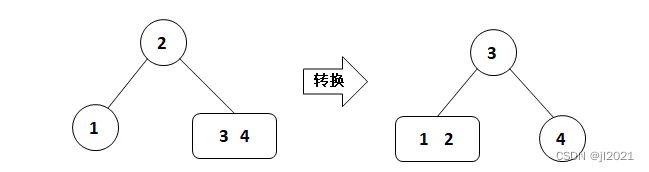
（1）插入的节点比现有的两个节点都大，新插入的节点连接到右边子树上，颜色反转。
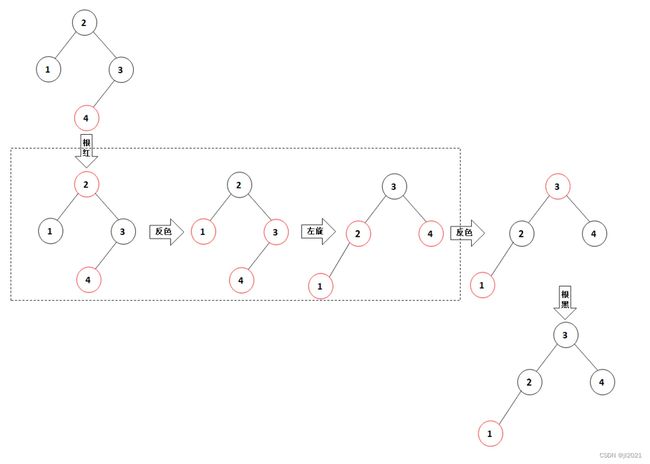
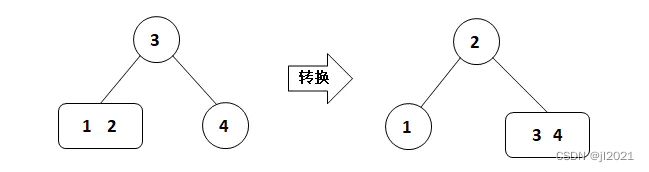
（2）插入的节点比现有的两个节点都小，新插入的节点连接到最左侧，中间节点右旋，颜色反转。
（3）插入的节点的值位于两个节点之间，新节点插入到左侧节点的右子节点。先以中间节点左旋至情况2，再中间节点右旋，颜色反转。
3-node节点底部插入新的节点，可能会导致父节点不满足红黑树的特点(完美平衡)，可以从下往上回溯更新节点的颜色(与AVL判断平衡因子更新树高相似)，直到平衡。
- 3-node节点底部插入新的节点的连锁反应实例1
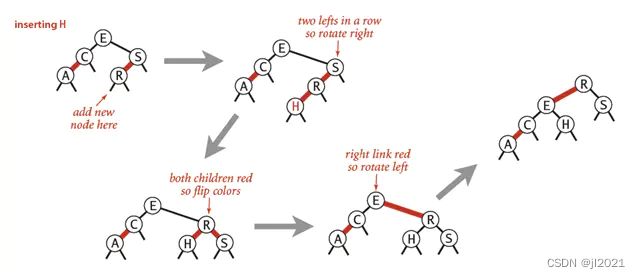
- 3-node节点底部插入新的节点的连锁反应实例2
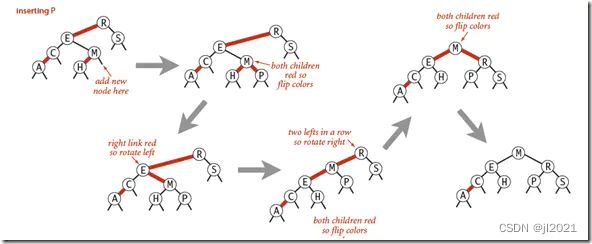
- 步骤：
（1）执行标准的二叉查找树插入操作，新插入的节点元素用红色标识。
（2）如果需要对4-node节点进行旋转操作
（3）如果需要，调用FlipColor方法将红色节点提升
（4）如果需要，左旋操作使红色节点左倾。
（5）在有些情况下，需要递归调用Case1 Case2，来进行递归操作。 - 平衡操作
（1）如果节点的右子节点为红色，且左子节点位黑色，则进行左旋操作
（2）如果节点的左子节点为红色，并且左子节点的左子节点也为红色，则进行右旋操作
（3）如果节点的左右子节点均为红色，则执行FlipColor操作，提升中间结点。
红黑树能够保证符号表的所有操作即使在最坏的情况下都能保证对数的时间复杂度，也就是树的高度。
- 最坏情况
红黑树中除了最左侧路径全部是由3-node节点组成，即红黑相间的路径长度是全黑路径长度的2倍。红黑树的高度不超过2lgN
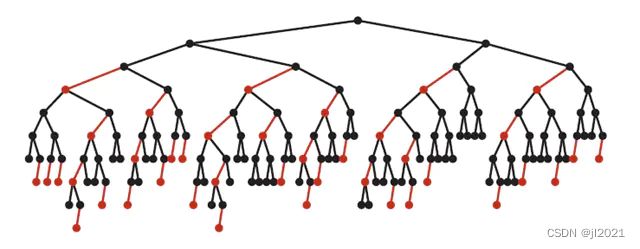
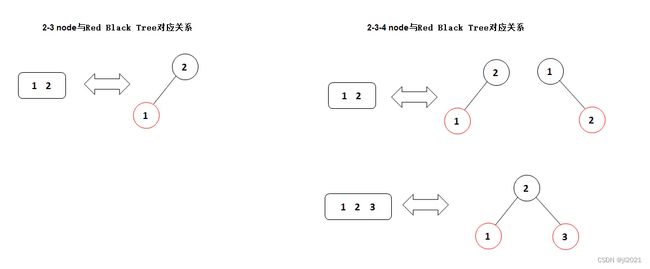
- 2-3 nodes树与RB树关系
2-3 nodes树中的4-node分裂成3个2-node，并让中间节点上移；等价于红黑树中的左右旋转；
2-3 nodes树中间节点上移与父节点融合过程；等价于红黑树中的反色操作。
5.2.7 查找
与BST一致。
5.2.8 删除
删除需要保证删除节点是非2-node的叶子节点，即必须是3-node和4-node。所以查找过程需要把过程中的2-node转化成3-node和4-node，删除后，在把3-node和4-node还原。
- 实例
#include right:root->left,val);
}
Node* Remove(Node* root,const T& val) {
if(nullptr == root) return nullptr;
if(root->val > val) {
if(!IsRed(root->left) && !IsRed(root->left->left)) root = MoveRedLeft(root);
root->left = Remove(root->left,val);
}else {
if(IsRed(root->left)) root = RotateRight(root);
if(val == root->val && nullptr == root->right) {delete root; return nullptr;}
if(!IsRed(root->right) && !IsRed(root->right->left)) root = MoveRedRight(root);
if(val == root->val){
T minval = Minimun(root->right);
root->val = minval;
root->right = Remove(root->right,minval);
// root->right = DeleteMin(root->right);
}else{
root->right = Remove(root->right,val);
}
}
return Balance(root);
}
Node* DeleteMin(Node* root) {
if(nullptr == root) throw runtime_error("root is null");
Node* prev = nullptr;
Node* cur = root;
while(nullptr != cur->left) {
prev = cur;
cur = cur->left;
}
delete cur;
return root;
}
T Minimun(Node* root) {
if(nullptr == root) throw runtime_error("root is null");
while(nullptr != root->left) root = root->left;
return root->val;
}
T Maximun(Node* root) {
if(nullptr == root) throw runtime_error("root is null");
while(nullptr != root->right) root = root->right;
return root->val;
}
Node* Insert(Node* root,const T& val) {
if(nullptr == root) return new Node(val);
if(root->val>val) {
root->left = Insert(root->left,val);
} else {
root->right = Insert(root->right,val);
}
return Balance(root);
}
// P Q
// / \ / \
// q C A p
// / \ / \
// A B B C
Node* RotateRight(Node* root){
Node* p = root;
Node* q = p->left;
Node* b = q->right;
q->right = p;
p->left = b;
q->color = p->color;
p->color = RED;
return q;
}
// P Q
// / \ / \
// A q p C
// / \ / \
// B C A B
Node* RotateLeft(Node* root){
Node* p = root;
Node* q = p->right;
Node* b = q->left;
q->left = p;
p->right = b;
q->color = p->color;
p->color = RED;
return q;
}
bool IsRed(Node* root){
return nullptr!=root && root->color==RED;
}
Node* FiipColor(Node* root) {
if(IsRed(root->left) && IsRed(root->right)) {
root->left->color = BLACK;
root->right->color = BLACK;
root->color = RED;
}else if(!IsRed(root->left) && !IsRed(root->right)) {
root->left->color = RED;
root->right->color = RED;
root->color = BLACK;
}
return root;
}
// 大写代表黑色，小写代表红色
// P P P B
// / \ / \ / \ / \
// A Q a q a b p q
// / / \ /
// b b q a
Node* MoveRedLeft(Node* root){
root = FiipColor(root);
if(IsRed(root->right->left)){
root->right = RotateRight(root->right);
root = RotateLeft(root);
}
return root;
}
// P P Q
// / \ / \ / \
// Q B q b a p
// / / \
// a a b
Node* MoveRedRight(Node* root){
root = FiipColor(root);
if(IsRed(root->left->left)){
root = RotateRight(root);
}
return root;
}
void Preorder(Node* root){
if(nullptr == root) return;
if(root->left) {
cout << root->val << "--" << root->left->val;
if(root->left->color==RED) cout << "[color=red]";
cout << endl;
}
if(root->right) {
cout << root->val << "--" << root->right->val;
if(root->right->color==RED) cout << "[color=red]";
cout << endl;
}
Preorder(root->left);
Preorder(root->right);
}
Node* Balance(Node* root){
if(IsRed(root->right) && !IsRed(root->left)) root = RotateLeft(root);
if(IsRed(root->left) && IsRed(root->left->left)) root = RotateRight(root);
if(IsRed(root->left) && IsRed(root->right)) root = FiipColor(root);
return root;
}
};
int main() {
RBTree<int> intbst;
int arr[] = {1,3,5,7,2,4,8};
for(auto n:arr){
intbst.Insert(n);
}
intbst.Print();
int n;
while(cin >> n) {
intbst.Remove(n);
intbst.Print();
}
}
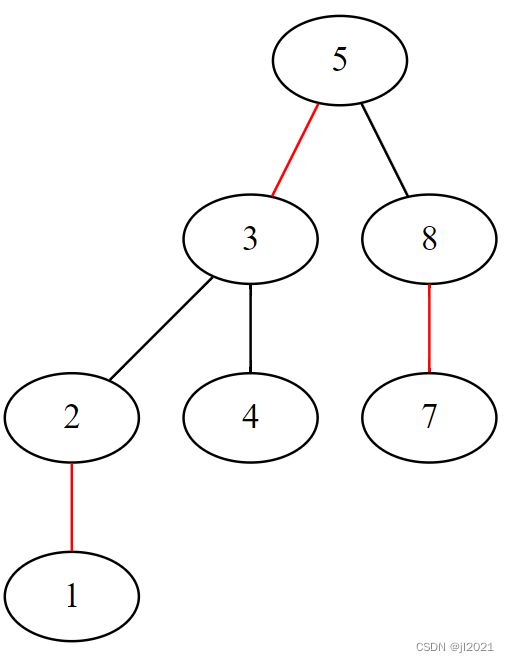
结果：
5--3[color=red]
5--8
3--2
3--4
2--1[color=red]
8--7[color=red]
树：
删除结点4
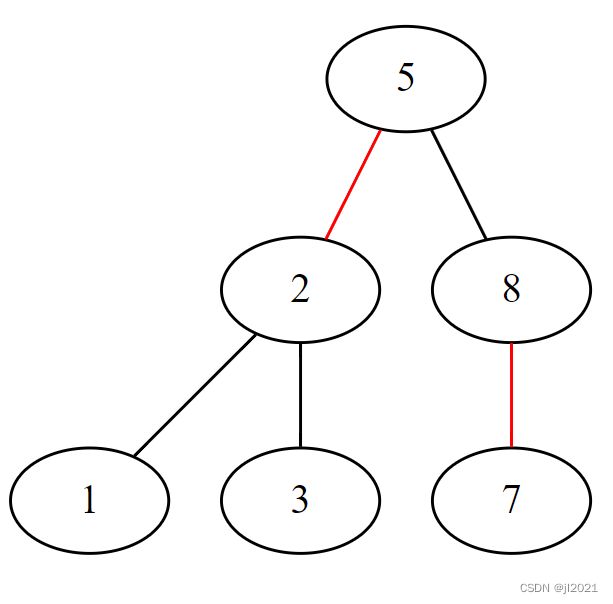
5--2[color=red]
5--8
2--1
2--3
8--7[color=red]
删除后的树：
再删除结点2：
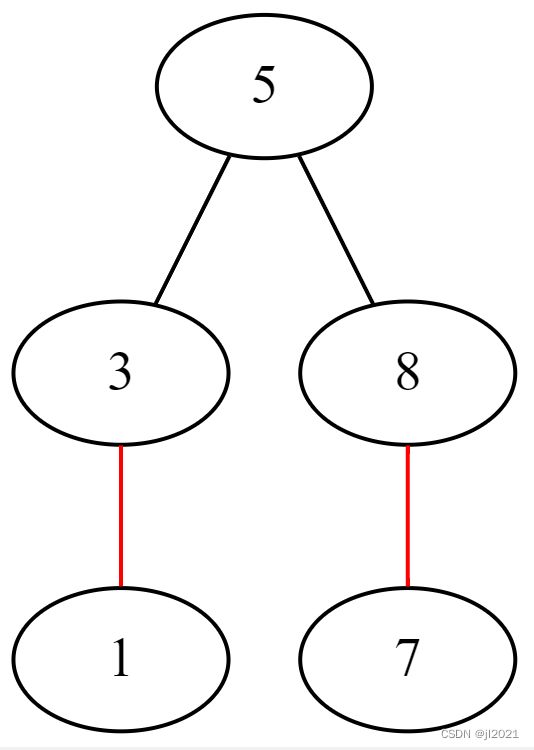
5--3
5--8
3--1[color=red]
8--7[color=red]
5.2.9 插入 vs. 删除
- 插入操作
| 操作 | 目的 | 改变项 | 保持项 | 执行条件 |
|---|---|---|---|---|
| 左旋/右旋 | 调节平衡,使之符合红黑树规定 | 节点的位置和颜色 | 始终保持BST特点 | 红节点不满足红黑树规定 |
| 颜色反转 | 调节平衡,使之符合红黑树规定(等价于2-3树4节点差分) | 改变节点的颜色 | 始终保持BST特点 | 红节点不满足红黑树规定 |
- 删除操作
| 操作 | 目的 | 改变项 | 保持项 | 执行条件 |
|---|---|---|---|---|
| 左旋/右旋 | 旋转红节点到要删除的分支，便于后续删除 | 节点的位置和颜色 | 始终保持BST特点 | 删除右子树节点，左子树的根节点为红节点时。 |
| 颜色反转 | 增加可使用的红节点(等价于2-3树节点4节点组合) | 改变节点的颜色 | 始终保持BST特点 | 左右子节点为黑节点时 |
| 红节点移动 | 移动红节点到要删除的分支，便于后续删除 | 节点的位置和颜色 | 始终保持BST特点 | 向下查找删除节点，当前子树连续两个黑节点时。 |