机器学习笔记-Logistic分类

机器学习笔记-Logistic分类

作者：星河滚烫兮

我们知道，回归模型一般是去根据已有的标记数据去预测新事物。Logistic回归模型因为历史原因有“回归”二字，但其实是一个分类模型。而Logistic分类与其他分类模型比如聚类又有什么区别呢？Logistic分类是有监督学习，必须需要人工标注；聚类则是无监督学习，只需要原始自然数据不需要标签。Logistic分类包括二分类与多分类，本篇文章重点关心二分类算法的实现，多分类我们可以通过简单的二分类的组合去实现。

一、线性回归可以解决分类问题吗？

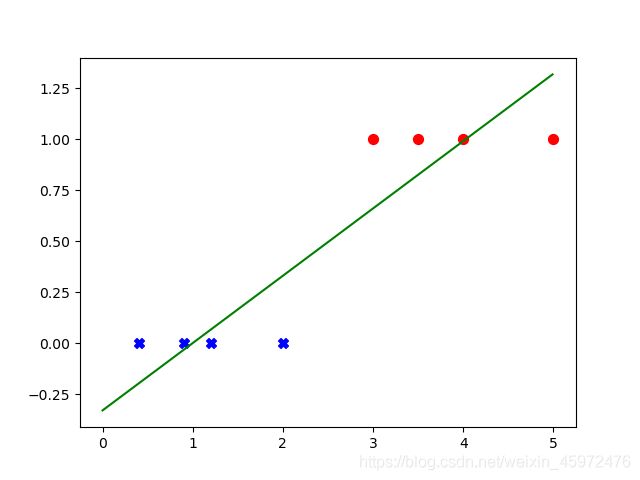
我们如果使用简单的线性回归模型想要解决分类二分类问题，对于分布密集的数据点效果还可以接受，但是一旦数据点分散不均匀或者有离群点，那么线性回归效果会非常差，简单来说是因为离群点对于线性模型的惩罚力度过大且线性模型输出区间在R上，所以最终得到的曲线像被拉伸了一样，我们看下面这个简单的例子。
设当输出y>0.5时该物品属于‘1’类，当y<=0.5时该物品属于‘0’类。

1. 当数据点密集分布时：
   
   从这个图中我们可以发现，两种类别的物品分布密集，没有离群点，所以分类效果较为理想。

2. 当数据点分散或有离群点时：
   
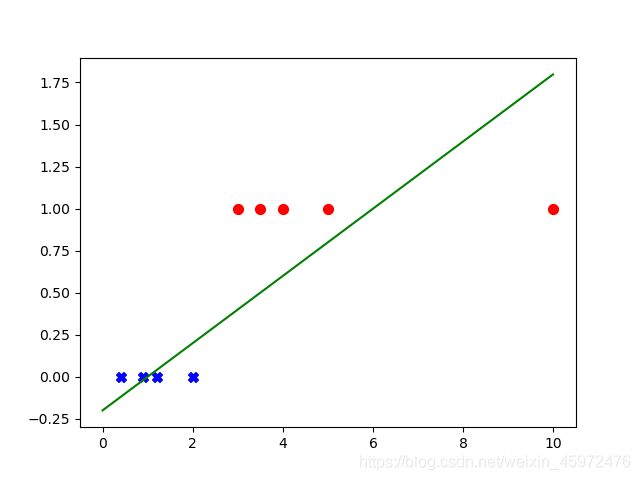
   在原有数据集中我们加入了一个离群点，得到了上图的曲线，我们可以发现，此离群点完全符合现实逻辑，具有合理性，然而仅仅添加了一个离群点就使得曲线被严重“拉伸”，也就是离群点对线性回归惩罚力度过大，如果仅仅是因为惩罚力度过大，尚且不至于导致上图的严重错误分类，更因为线性模型是发散的，输出区间->R,所以线性回归模型不能够很好的应用于分类问题，我们从这里就可以想到去寻找到一种收敛函数，输出介于[0,1]之间。

二、Logistic回归模型简述

Logistic回归又叫逻辑回归，本质上其实是sigmod激活函数，即：$y=\frac{1}{1+e^{-{\theta }^{T}x}}$.其中，$\theta =\left(\begin{array}{c}{\theta }_0\\ \begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\end{array}\\ {\theta }_m\end{array}\right)$，$x=\left(\begin{array}{c}{x}_0\\ \begin{array}{c}{x}_1\\ x_2\\ ⋮\end{array}\\ x_m\end{array}\right)$.m就是特征向量的特征数，我们展开向量积${\theta }^{T}x$有：
${\theta }^{T}x={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+\cdots +{\theta }_m{x}_m$
为了方便用列向量整齐的表示，我们引入$x_0=1$。设$z={\theta }^{T}x$，则我们有：$y=\frac{1}{1+e^{-z}}$
画出y关于z的函数图像有：

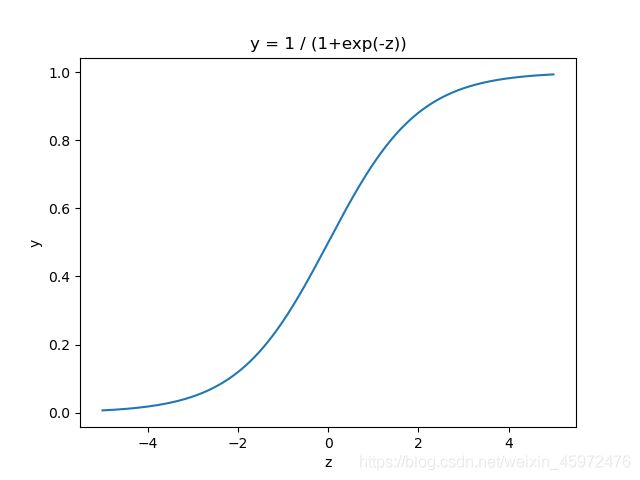
从函数与图像我们可以发现，sigmod曲线的特点是：
当$z\to -\infty$时，$y\to 0$；当$z\to +\infty$时，$y\to 1$.y的取值范围为[0,1],由此我们可以简单的认为，y的值就是分类结果的概率。
比如我们预测明天是否会下雨，1代表下雨，0代表不下雨，那么我们将特征向量积${\theta }^{T}x$作为z传进预测函数$y=\frac{1}{1+e^{-z}}$内，将会的到一个y值，对应上图中的某个点，假如我们的得到了y=0.8，我们就可以简单的认为明天下雨的概率为0.8（这里因为的“概率”其实并不严谨，因为分布不均匀）。接着，我们凭借直觉（对称性）可以很自然的设置：y>0.5则判定为1，y<=0.5则判定为0，所以，我们得到最终结果：明天会下雨（结果为1）。

三、深入Logistic回归

从上面的简述我们不难发现，在$z={\theta }^{T}x={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+\cdots +{\theta }_m{x}_m$中，我们已知特征向量$x=\left(\begin{array}{c}{x}_0\\ \begin{array}{c}{x}_1\\ x_2\\ ⋮\end{array}\\ x_m\end{array}\right)$，一旦我们确定了特征向量的参数$\theta =\left(\begin{array}{c}{\theta }_0\\ \begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\end{array}\\ {\theta }_m\end{array}\right)$，那么我们便可以通过此模型去解决分类问题。关键是如何确定参数\theta，我们在此还是使用梯度下降的方法，实现代价函数的最小化，使其无限收敛于最小值。
在此，我们设定以下函数：

1). 假设函数：$h\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}x}}$

2). 单样本损失函数：$cost\left(h\left(x\right),y\right)=-y\ln h\left(x\right)-\left(1-y\right)\ln \left(1-h\left(x\right)\right)$

3). 代价函数：$J\left(\theta \right)=\frac{1}{n}\times {\sum }_{i=1}^{n}cost\left(h\left(x^i\right),y^i\right)$

4). 梯度下降：${\theta }_j={\theta }_j-\alpha \frac{\partial J\left(\theta \right)}{\partial {\theta }_j}.$
其中，n为样本个数，m为特征个数，$x=\left(\begin{array}{c}{x}_0\\ \begin{array}{c}{x}_1\\ x_2\\ ⋮\end{array}\\ x_m\end{array}\right)$，$\theta =\left(\begin{array}{c}{\theta }_0\\ \begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\end{array}\\ {\theta }_m\end{array}\right)$.
对于假设函数h(x)与梯度下降，我们应该没有疑问。而对于代价函数，回忆在线性回归中，其代价函数$J\left(\theta \right)=\frac{1}{2n}{\sum }_{i=1}^n{\left[h\left(x^i\right)-y^i\right]}^2$，称为平方损失函数，因为对于线性回归，预测函数$h\left(x\right)={\theta }^{T}x=ax+b$,这样的多项式形式代入进代价函数中进行梯度下降求偏导数的过程很简单。但是对于Logistic回归，我们如果仍然采用平方损失函数，我们将Logistic回归的假设函数$h\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}x}}$代入进平方损失函数中会发现，$J\left(\theta \right)=\frac{1}{2n}{\sum }_{i=1}^n{\left[\frac{1}{1+e^{-{\theta }^T{x}^i}}-y^i\right]}^2$会变得很复杂，同时，梯度下降函数中的偏导数项也非常复杂，除此之外，我们应该记得，损失函数应该要全局收敛于某一个值，也就是要保证损失函数$J\left(\theta \right)$有且仅有一个极值点(最小值)，我在这里不过多进行Logistic回归平方损失函数收敛域的推导，下面我利用python简单的将其图像绘制出来（分别绘制$y^i=0$，$y^i=1$），大家可以直观的观察到：

曲线极其陡峭，当然，因为$y^i=0，1$两个离散值，所以最真实图像不会收敛在上图中的0处，但是因为用平方损失函数表示出来的曲线极其陡峭，采用梯度下降会很难进行，所以我们需要寻找一种新的损失函数。我们都知道，指数函数增长趋势很快，因此造成了上图那样陡峭，于是我们可以用对数函数$\ln x$对假设函数$h\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}x}}$进行降维，降低其增长速度，于是我们有了以下单样本损失函数$cost\left(h\left(x\right),y\right)$：
$cost\left(h\left(x\right),y\right)=\{\begin{array}{ll}-lnh(x)& \text{, }y=1\\ -ln(1-h(x))& \text{, }y=0\end{array}$
将其图像绘制出来（分别绘制$y^i=0，y^i=1$）有：

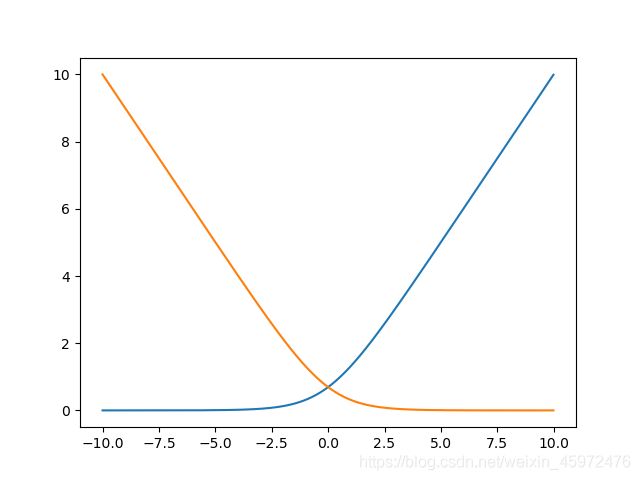
从上图我们可以看出，损失函数变化趋势相对平滑，这就是我们降维后的结果。下面我们来看一看单样本损失函数的物理意义：

• 当y=1时：$cost\left(h\left(x\right),y\right)=-\ln h\left(x\right)$，对应上图黄线，观察发现，若$h\left(x\right)\to 0$,则$cost\left(h\left(x\right),y\right)\to +\infty$，也就是分类完全错误，我们给模型一个非常大的惩罚；若$h\left(x\right)\to 1$,则$cost\left(h\left(x\right),y\right)\to 0$，也就是分类完全正确，此样本损失值cost=0。
• 同理，当y=0时：$cost\left(h\left(x\right),y\right)=-\ln \left(1-h\left(x\right)\right)$，对应上图蓝线，观察发现，若$h\left(x\right)\to 0,则cost\left(h\left(x\right),y\right)\to 0$，也就是分类完全正确，此样本损失值cost=0；若$h\left(x\right)\to 1$,则$cost\left(h\left(x\right),y\right)\to +\infty$，也就是分类完全错误，我们给模型一个非常大的惩罚。

到这里，我们已经能够理解为什么要选择对数损失函数。因为输入的y非0即1，所以我们可以把上面的分段对数损失函数合并（类似于信号的叠加），得到最终形式：
$cost\left(h\left(x\right),y\right)=-y\ln h\left(x\right)-\left(1-y\right)\ln \left(1-h\left(x\right)\right)$
最终的单样本损失函数就叫做交叉熵函数，意思是0和1两种状态的交叉计算。最后，我们将单样本损失函数求和取平均得到了模型的代价函数$J\left(\theta \right)=\frac{1}{n}\times {\sum }_{i=1}^{n}cost\left(h\left(x^i\right),y^i\right)$.

四、梯度下降中的偏导数项

为了编写代码，我们还需要计算出${\theta }_j={\theta }_j-\alpha \frac{\partial J\left(\theta \right)}{\partial {\theta }_j}$中的偏导数项$\frac{\partial J\left(\theta \right)}{\partial {\theta }_j}$，求导过程其实很简单，我将过程书写在纸上如下所示：

注意上下角标的区别，上角标i表示第i个样本，下角标j表示某样本的第j个特征。

五、代码：

这里我使用了只包含一个特征的输入，构建了一个最简单的Logistic二分类模型，后续我会继续更新包含多个特征的多元Logistic回归模型代码，以及多分类模型。

import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt


class Logistic:
    """
    这是一个logistic二分类模型
    """
    def __init__(self):
        # 定义二分类数据集，其中：x仅有一个特征
        self.dataset_x = np.array([0.1, 0.33, 0.4, 1.5, 2.6, 5, 6.6, 7, 9, 11.3, 11.5, 15])
        self.dataset_y = np.array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1])
        # 定义x参数θ0,θ1
        self.a = 0
        self.b = 0
        # 定义模型参数
        self.r = 0.15                                    # 学习率r
        self.n = len(self.dataset_x)                    # 样本数量n
        self.m = 1                                      # 样本特征数m
        self.EPOCH = 20000                                 # 迭代次数

    def h(self, x):
        """
        logistic二分类假设函数: h(x)=1/(1+exp(-z)), z=θ0+θ1*x1+θ2*x2+...+θm*xm.(可简写为向量积形式)
        :param x: 输入自变量x数组
        :return: 预测值数组
        """
        y = 1 / (1+np.exp(-(self.a+self.b*x)))
        return y

    def cost(self, x, y):
        """
        损失函数(不同于代价函数J): cost = -y*ln(h(x)) - (1-y)*ln(1-h(x))
        :param x: 输入自变量x
        :param y: 输入人工标记值y数组
        :return: 损失值(0~1)数组
        """
        h = self.h(x)
        cost = -y*np.log(h) - (1-y)*np.log(1-h)
        return cost

    def gradient(self, x, y):
        """
        梯度下降算法: θj = θj - α*(dJ/dθj)
        :param y:输入人工标记y数组
        :param x:输入自变量x数组(x0=1)
        :return:无返回值,更新参数
        """
        temp1 = (1/self.n) * np.sum((self.h(x)-y)*1)
        temp2 = (1/self.n) * np.sum((self.h(x)-y)*x)
        self.a = self.a - self.r*temp1
        self.b = self.b - self.r*temp2

    def training(self, x, y):
        """
        训练模型
        :param x: 输入自变量x
        :param y: 输入人工标记y
        :return: 无返回值
        """
        for i in range(self.EPOCH):
            self.gradient(x, y)
            lost = 1/self.n * np.sum(self.cost(x, y))
            print(f"第{i}次迭代损失值为:{lost}, 参数: a={self.a}, b={self.b}")

    def display(self, x, y):
        plt.scatter(x=x, y=y)
        newx = np.arange(0, 20, 0.01)
        newy = self.h(newx)
        plt.plot(newx, newy)
        plt.show()


A = Logistic()
A.training(A.dataset_x, A.dataset_y)
print(A.h(A.dataset_x))
A.display(A.dataset_x, A.dataset_y)

拟合结果如下：

以上就是我学习机器学习Logistic回归的学习笔记，包含了我个人的一些想法和理解，如果文章有错误还请大家指正，非常希望能与各位交流，共同进步 ^ _ ^

参考文献：吴恩达机器学习 https://study.163.com/course/courseMain.htm?courseId=1210076550.