概率论基础3
文章目录
- 随机过程
-
- simple random walk
- 马尔可夫链
-
- Stochastic Matrices
- stationary distributions
- martingale
- discrete-time random process
- continued-time random process
- regression analysis
-
-
- multiple regression
- General Linear Model(GLM)
-
随机过程
随机过程定义非常简单如下
collection of time functions with assciate probability distribution
换句话说
random process is collection of random variables in time
此时random process定义为如下
X 0 , X 1 , X 2 . . . X n X_0,X_1,X_2...X_n X0,X1,X2...Xn aka discrete-time
or
{ X t } t > = 0 \{X_t\}_{t>=0} {Xt}t>=0 aka continued-time
随机过程是描述多个random vairable的工具,多个random variable随着时间排序组成random process,
random process中的random variable也可以有关系,组成样本函数,我们下面有3个random process的sample function,其描述了随着时间的变化,样本的变化
1. f ( t ) = t f(t)=t f(t)=t with prob 1
- f ( t ) = t f(t)=t f(t)=t for all t with prob 1/2
f ( t ) = − t f(t)=-t f(t)=−t for all t with prob 1/2
- for each t, f ( t ) = t , o r − t f(t)=t,or-t f(t)=t,or−t,with prob 1/2
我们为了能狗预测未来,可以通过随机过程预测未来的情况,假设上述三个式子和图片代表的是股票价格,那么
第一个毫无疑问后续都是上升的
第二个式子有1/2的可能一直上升或者有1/2的可能一直下降,这个我们通过前面的趋势判断就行
第三个式子就不好判断了,他的意思是后续的时间内有1/2可能在y=t上,有1/2可能在y=-t上,所以他是一个上下震荡的模型
simple random walk
首先我们有非常多random variable Yi
且 Y i Y_i Yi是i.i.d的,random variable中只有2个数字分别是1和-1,每个prob各占1/2
for each t X t = ∑ i = 1 t Y i X_t=\sum_{i=1}^tY_i Xt=∑i=1tYi, X 0 = 0 X_0=0 X0=0
X 0 , X 1 , X 2 X 3 , . . . X_0,X_1,X_2X_3,... X0,X1,X2X3,...is called simple random walk,当我们画出图就非常的有意思了(我们假设是离散的情况)
首先 X 0 = 0 X_0=0 X0=0毫无疑问, X 1 = Y 0 + Y 1 X_1=Y_0+Y_1 X1=Y0+Y1,因为 Y 1 Y_1 Y1有百分之50的可能为1,百分之50的可能是-1,所以 X 1 = − 1 o r 1 X_1=-1or1 X1=−1or1,随后的 X 2 X_2 X2到 X n X_n Xn直接类似,要注意的是 Y i Y_i Yi有50%的可能为1,百分之50的可能为-1( X i X_i Xi加上1或者减去1),所以我们画出的图片也是一个random walk的可能上升可能下降如下
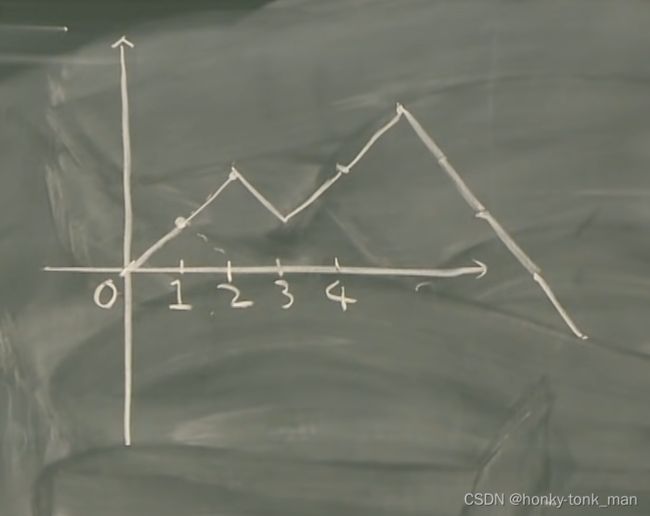
上图图片是 X 1 = 1 X_1=1 X1=1, X 2 = 1 X_2=1 X2=1, X 3 = − 1 X_3=-1 X3=−1, X 4 = 1 X_4=1 X4=1…然后累加,每一个 X i X_i Xi都是一个random variable,百分之50的可能为1,百分之50的可能为-1,这样累加后组成我们的随机过程,这也是随机过程的本质(时间离散情况)
还记得中心限制 定理吗(CLT),当我们的random variable加在一起越来越多,的时候会是Normal distribution的,既然提到Normal distribution那么我们就要求其mean和variance
假设 S t = X 1 + X 2 + . . . + X t S_t=X_1+X_2+...+X_t St=X1+X2+...+Xt,那么mean(S_n)= t E [ X 1 ] tE[X_1] tE[X1],因为 X t X_t Xt不是-1就是1,且各占百分之50,那么 E [ X 1 ] = 0 E[X_1]=0 E[X1]=0,且mean(S_n)= t E [ X 1 ] = 0 tE[X_1]=0 tE[X1]=0
对于方差 σ ( S t ) 2 = t V a r [ X 1 ] \sigma(S_t)^2=tVar[X_1] σ(St)2=tVar[X1],因为Var[X1]= 1 2 ( − 1 − 0 ) 2 + ( 1 − 0 ) 2 = 1 \frac{1}{2}(-1-0)^2+(1-0)^2=1 21(−1−0)2+(1−0)2=1,所以标准差 σ = + − t \sigma=+-\sqrt{t} σ=+−t,因为标准差是表示random vairable波动频率的,所以换句话说我们的random process开始波动小后面波动越来越大,但是不超过y=t和y=-t 2个边界值

马尔可夫链
首先我们一些量化策略都是通过所有的过去数据去预测未来数据,而马尔可夫链只需要用最近的数据去预测未来的数据
马尔可夫链的定义如下,假如t是当前的时间,t之前的 X t − 1 X_{t-1} Xt−1, X t − 2 X_{t-2} Xt−2等都是历史数据,那么我们的未来数据 X t + 1 X_{t+1} Xt+1为 P ( X t + 1 = S ∣ X t ) = P ( X t + 1 = S ∣ X 0 , X 1 . . . X t ) P(X_{t+1}=S|Xt)=P(X_{t+1}=S|X_0,X_1...X_t) P(Xt+1=S∣Xt)=P(Xt+1=S∣X0,X1...Xt),满足这样的random variable才是马尔可夫链
如果通过所有的历史数据去预测未来数据公式是这样的 P ( X t + 1 = S ∣ X 0 , X 1 . . . X t ) P(X_{t+1}=S|X_0,X_1...X_t) P(Xt+1=S∣X0,X1...Xt)
simple random walk是马尔可夫链因为在时间节点t的时候我们只有2个选择分别是 S = X t + 1 S=X_t+1 S=Xt+1或者 S = X t − 1 S=X_t-1 S=Xt−1,所以无论你在只有t这个当前时间点的数据还是有前面历史所有时间点的数据t+1这个未来的时间点结果都一样,要么加一要么减一
Stochastic Matrices
Stochastic Matrices aka probability matrix,transition matrix
首先概率矩阵是一个二阶矩阵每一行都是一个概率向量,概率P如下
[ P 1 , 1 P 1 , 2 . . . P 1 , j . . . P 1 , a P 2 , 1 P 2 , 2 . . . P 2 , j . . . P 2 , a P 3 , 1 P 3 , 2 . . . P 3 , j . . . P 3 , a . . . P i , 1 P i , 2 . . . P i , j . . . P i , a . . . P a , 1 P a , 2 . . . P a , j . . . P a , a ] \begin{bmatrix} P_{1,1} & P_{1,2} & ... &P_{1,j}&...&P_{1,a}\\ P_{2,1} & P_{2,2} & ... &P_{2,j}&...&P_{2,a}\\ P_{3,1} & P_{3,2} & ... &P_{3,j}&...&P_{3,a}\\ ...\\ P_{i,1} & P_{i,2} & ... &P_{i,j}&...&P_{i,a}\\ ...\\ P_{a,1} & P_{a,2} & ... &P_{a,j}&...&P_{a,a} \end{bmatrix} P1,1P2,1P3,1...Pi,1...Pa,1P1,2P2,2P3,2Pi,2Pa,2...............P1,jP2,jP3,jPi,jPa,j...............P1,aP2,aP3,aPi,aPa,a
其中每一行都是一个概率向量,相加为1(想一下二重random variable)
且 P ( j ∣ i ) = P i , j P(j|i)=P_{i,j} P(j∣i)=Pi,j,例如 P ( 1 , 2 ) P(1,2) P(1,2)为 P ( 2 ∣ 1 ) P(2|1) P(2∣1)已知1求2的概率
∑ j = 1 a P i , j = 1 \sum_{j=1}^aP_{i,j}=1 ∑j=1aPi,j=1
i可能比j大也可能比j小,用这个概率矩阵的目的是为了观察从i到j( P ( j ∣ i ) P(j|i) P(j∣i))的概率变化
而概率矩阵是先验统计得到的
关于有Stochastic Matrices的马尔可夫链的另一个例子如下
假如我们的城市有3个共享单车的停车点(A,B,C),我们通过观察统计了解到
A点的车百分之30留在了A点,百分之50去了B点,百分之20去了C点
B点的车百分之10留在了A点,百分之60留在了B点,百分之30去了
C点的车百分之10去了A点,百分之10去了B点,百分之80留在了C点
此时我们根据上述的观察,可以得到Stochastic Matrices T如下
[ 0.3 0.5 0.2 0.1 0.6 0.3 0.1 0.1 0.8 ] \begin{bmatrix} 0.3 & 0.5 & 0.2\\ 0.1 & 0.6 & 0.3\\ 0.1 & 0.1 & 0.8\\ \end{bmatrix} 0.30.10.10.50.60.10.20.30.8
假设我们随机过程的函数的t是按照天数来衡量的
那么我们第一天的A,B,C三个站点自行车分布情况如下
V 0 = [ 0.3 , 0.45 , 0.25 ] V_0=[0.3 ,0.45,0.25] V0=[0.3,0.45,0.25]
经过一天后我们估算其后一天的自行车分布情况如下
V 1 = V 0 T = [ 0.16 , 0.445 , 0.395 ] V_1=V_0T=[0.16,0.445,0.395] V1=V0T=[0.16,0.445,0.395]
假设我们从 V 0 V_0 V0开始估算后天自行车分布的情况(这里跨度2天,一天一个step,这里是2个step)公式如下
V 2 = V 1 T = V 0 T T = V 0 T 2 V_2=V_1T=V_0TT=V_0T^2 V2=V1T=V0TT=V0T2
所以我们如果是T+2那么我们的概率矩阵要平方
记住!概率矩阵要求样本空间是有限的!!!,比如上述例子中样本空间就3个,A,B,C,而random walk样本空间是无限的,因为样本空间的样本不断地从0开始在加一减一(random walk中的样本从0到-n或者+n ),所以他没有概率矩阵
stationary distributions
stationary就是stationary矩阵(概率矩阵)中的那个stationary ,他是马尔可夫链中的一个概率分布
在了解stationary distribution之前我们先说一个概念叫做Π,这个Π不是圆周率中的3.141592…而是一个向量,他表示马尔可夫链中所有的状态(space sample中所有样本)的一个状态(概率),比如上面共享单车车站的例子,我们的Π是一个向量,这个向量包含了站点A,B,C各自目前拥有自行车的比例,那么stationary distributions表示什么呢?假设概率矩阵(transition matrix)为T那么, Π T = Π ΠT=Π ΠT=Π,侧面证明Π这个向量是稳定的,经过概率矩阵后不变,换句话说假如我们共享单车站点A,B,C三个站点目前单车的比例正好构成一个Π,那么他就是stationary distributions的
如何计算Π呢?还是共享单车的例子,站点的transition matrix T如下
[ 0.3 0.5 0.2 0.1 0.6 0.3 0.1 0.1 0.8 ] \begin{bmatrix} 0.3 & 0.5 & 0.2\\ 0.1 & 0.6 & 0.3\\ 0.1 & 0.1 & 0.8\\ \end{bmatrix} 0.30.10.10.50.60.10.20.30.8
向量Π的三个元素分别为 Π A Π_A ΠA, Π B Π_B ΠB, Π C Π_C ΠC等
Π A Π_A ΠA先看有那个样本走向(step to)样本A,分别是A->A,B->A,C->A,概率分别是0.3,0.1,0.1,那么 Π A = 0.3 Π A + 0.1 Π B + 0.1 Π C Π_A=0.3Π_A+0.1Π_B+0.1Π_C ΠA=0.3ΠA+0.1ΠB+0.1ΠC=> 0.7 Π A = 0.1 Π B + 0.1 Π C 0.7Π_A=0.1Π_B+0.1Π_C 0.7ΠA=0.1ΠB+0.1ΠC
Π B Π_B ΠB先看有那个样本走向(step to)样本B,分别是A->B,B->B,C->B,概率分别是0.5,0.6,0.1,那么
Π B = 0.5 Π A + 0.6 Π B + 0.1 Π C Π_B=0.5Π_A+0.6Π_B+0.1Π_C ΠB=0.5ΠA+0.6ΠB+0.1ΠC=> 0.4 Π B = 0.5 Π A + 0.1 Π C 0.4Π_B=0.5Π_A+0.1Π_C 0.4ΠB=0.5ΠA+0.1ΠC=> − 0.5 Π A = − 0.4 Π B + 0.1 Π C -0.5Π_A=-0.4Π_B+0.1Π_C −0.5ΠA=−0.4ΠB+0.1ΠC
Π C Π_C ΠC先看有那个样本走向(step to)样本C,分别是A->C,B->C,C->C,概率分别是0.2,0.3,0.8,那么
Π C = 0.2 Π A + 0.3 Π B + 0.8 Π C Π_C=0.2Π_A+0.3Π_B+0.8Π_C ΠC=0.2ΠA+0.3ΠB+0.8ΠC=> 0.2 Π C = 0.2 Π A + 0.3 Π B 0.2Π_C=0.2Π_A+0.3Π_B 0.2ΠC=0.2ΠA+0.3ΠB=> − 0.2 Π A = 0.3 Π B − 0.2 Π C -0.2Π_A=0.3Π_B-0.2Π_C −0.2ΠA=0.3ΠB−0.2ΠC
martingale
首先我们的martingale是一种特殊的随机过程,假设我们的随机过程满足下面的式子那么他就是maringale的
X t = E [ X t + 1 ∣ F t ] X_t=E[X_{t+1}|F_t] Xt=E[Xt+1∣Ft],其中t>=0,t也可以看成是当前的时间t+1可以看成未来的时间, F t = X 0 , X 1 , X 2 . . . X t F_t={X_0,X_1,X_2...X_t} Ft=X0,X1,X2...Xt
通俗的话讲,就是未来的事件发生的值的期望值(sample mean)等于当前所发生的值
random walk是martingale的
例如,我们有一个股票在当天t,的价格是4元( X t X_t Xt),明天有1/3的概率涨到8元( X t + 1 X_{t+1} Xt+1),2/3的概率降低到2元( X t + 1 X_{t+1} Xt+1),我们可以计算t+1(明天)股票的期望值如下
E [ X t + 1 ] = 1 3 8 + 2 3 2 = 4 = X t E[X_{t+1}]=\frac{1}{3}8+\frac{2}{3}2=4=X_t E[Xt+1]=318+322=4=Xt
那么我们可以说这个随机过程是martingale的
假如 X t > E [ X t + 1 ] X_t>E[X_{t+1}] Xt>E[Xt+1]那么可以称这个随机过程是supermartingale的
假如 X t < E [ X t + 1 ] X_t
discrete-time random process
continued-time random process
regression analysis
我们用线性回归的目的是为了寻找2个dependent和independent variable之间的关系,以便预测未来的变化
我们之前看到过一些线性模型,其具体是2个random variable dependent,且相交,然后我们将已知的多个点在直角坐标轴上标出来,然后画出线,
y = a x + b y=ax+b y=ax+b
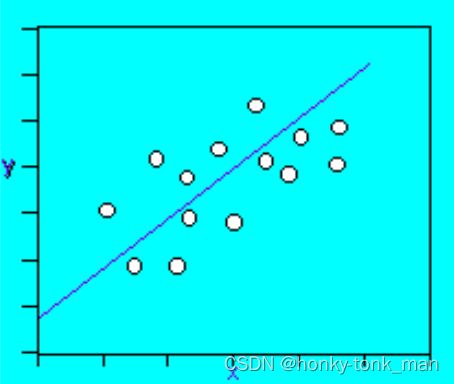
最后我们可以通过这个线预测我们未来数据的走向,关于线性模型还有一个参数是error(简称e)如下
y = a x + b + e y=ax+b+e y=ax+b+e
e是一个变量,其代表我们的线性方程到每个具体值的offset,如下图

上述也叫做simple regression,为什么simple因为他就一个predictors(independent random variable),就是上述的x,如下
Y ˉ = B 0 + B 1 X 1 + B 2 X 2 + B 3 X 3 + . . . + B k X k \bar{Y}=B_0+B_1X_1+B_2X_2+B_3X_3+...+B_kX_k Yˉ=B0+B1X1+B2X2+B3X3+...+BkXk
Y ˉ \bar{Y} Yˉ predicted value on the outcome variable Y
B 0 B_0 B0predicted value on Y when all X = 0
X k X_k Xkpredictor variables
B k B_k Bkunstandardized regression coefficients
multiple regression
既然有了simple regression那么就有multiple regression,multiple代表其有多个predictors(independent random variable)
General Linear Model(GLM)
GLM是一个非常有用的框架,其通过用来对比不同的variable是如何影响不同的连续variable的,GLM可以描述为下面的形式
D a t a = M o d e l + E r r o r Data = Model+Error Data=Model+Error
我们的GLM和上面讲的差不多但是!在GLM中讲述的不再是2个dependent的random variable了,而是一系列的random variable如下
y = b 0 + b x + e y=b_0+b_x+e y=b0+bx+e
y is a set of outcome variable
x is a set of pre-program variables or convariates
b0 is the set of intercepts


