【蓝桥杯 第十二届省赛Java B组】真题训练（A - H）

目录

A.ASC - 一眼答案

B.卡片 - 枚举

C.直线 - 数学 + 精度问题 + 字符串去重

D.货物摆放 - 分解因数 + 暴力枚举

E.路径 - 最短路 + 最小公倍数

1、朴素版dijkstra 

2、堆优化版dijkstra

3、spfa求最短路

F.时间显示 - 模拟

G.最少砝码 - 数学 + 找规律

H.杨辉三角形 - 组合数+二分

1、暴力40%

2、找规律+二分+组合数  100%

---

A.ASC - 一眼答案

题目：

已知A的ascii码是65，则L的ascii码是多少？

答案：76 

System.out.print((int)('L'-'A'));

B.卡片 - 枚举

题目：

思路：

将0~9每张牌的牌数设置成2021

cnt从1开始枚举数x，将x的每一位拆分出来，扣除相应的牌数

如果当某个数凑不出来时，break

则答案为cnt-1

import java.util.*;

public class Text //主类 
{
	static int N=550;
	static int res;
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		int[] num=new int[10];
		for(int i=0;i<10;i++) num[i]=2021;
		int cnt=1;
		boolean f=true;
		while(true)
		{
			int x=cnt;
			while(x>0)
			{
				int t=x%10;
				if(num[t]>0) num[t]--;
				else 
				{
					f=false;
					break;
				}
				x/=10;
			}
			if(f) cnt++;
			else break;
		}
		System.out.print(cnt-1);
	}
}

C.直线 - 数学 + 精度问题 + 字符串去重

题目：

思路：

答案：40257

直线用y=kx+b来唯一标识，用于double除法存在精度问题

而且java的set不能对类PII去重，因此采用字符串的去重方式

因为是填空题，n=20，m=21，因此直接暴力枚举每个点

我们先只考虑斜线（水平线条数=m+n）     x1!=x2&&y1!=y2

• 设kx=x1-x2，ky=y1-y2
•    注意！除法存在精度问题，因此我们以字符串分数形式存入
• 先算出g1=gcd（kx，ky），则存入s=ky/g1+"/"+kx/g1

• 将上述k代入y=kx+b中，得 同样化为字符串分数形式
• 设ba=kx*y-ky*x
• 先算出g2=gcd（ba，kx)，则存入s+=ba/g2+"/"+kx/g2

将字符串s存入set去重，最后答案就是  斜线+水平线=set.size()+m+n

package text;

import java.util.*;

public class Text //主类 
{
	static int N=550;
	static int res;
	
	public static int gcd(int a,int b)
	{
		return b!=0? gcd(b,a%b):a;
	}
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt(),m=sc.nextInt();
		Set st=new HashSet<>();
		List list=new ArrayList<>();
		
		for(int i=0;i

D.货物摆放 - 分解因数 + 暴力枚举

题目：

思路：

答案：2430

如果暴力三重for循环肯定会跑不完的

可以先预处理出n的因子存入数组

在这些因子里，三重for循环记录i*j*k==n的组合数

import java.util.*;

public class Text //主类 
{
	static int N=550;
	static int res;
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		long n=2021041820210418L;
		long[] a=new long[1100];
		int cnt=0;
		//先筛出n的所有因子
		for(long i=1;i<=n/i;i++)
			if(n%i==0)
			{
				a[cnt++]=i;
				if(n/i!=i) a[cnt++]=n/i;
			}
		
		//在因子里面找三个相乘=n
		for(int i=0;in) continue;
				for(int k=0;k

 

E.路径 - 最短路 + 最小公倍数

题目：

思路：

答案：10266837

最小公倍数=a*b/gcd(a,b)

可以用dijkstra或者spfa两种方法求最短路

1、朴素版dijkstra 

模板：

用邻接矩阵存图   初始化dist=0x3f   dist[1]=0  st[1]=1

循环n次

{

        找出未标记且距离源点最近的点

        标记该点

        用该点更新到其他相邻点的最短路

}

return dist[n]

import java.util.*;

public class Text //主类 
{
	static int N=2025;
	static int[][] g=new int[N][N];
	static int[] st=new int[N];
	static int[] dist=new int[N];
	
	public static int gcd(int a,int b)
	{
		return b!=0? gcd(b,a%b):a;
	}
	
	public static int dijkstra()
	{
		Arrays.fill(dist,0x3f3f3f3f);
		dist[1]=0;
		
		for(int i=0;i<2021;i++)
		{
			int t=-1;
			for(int j=1;j<=2021;j++)
			{
				if(st[j]==0&&(t==-1||dist[t]>dist[j]))
					t=j;
			}
			st[t]=1;
			
			for(int j=1;j<=2021;j++) dist[j]=Math.min(dist[j],dist[t]+g[j][t]);
		}
		
		return dist[2021];
	}
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		for(int i=1;i<=2021;i++) Arrays.fill(g[i],0x3f3f3f3f);
		
		for(int i=1;i<=2021;i++)
			for(int j=1;j<=2021;j++)
				if(Math.abs(i-j)<=21)
				{
					int t=i*j/gcd(i,j);
					g[i][j]=g[j][i]=t;
				}
		int res=dijkstra();
		System.out.print(res);
	}
}

2、堆优化版dijkstra

模板：

用邻接表存图   初始化dist=0x3f   dist[1]=0   st[1]=1

建立小顶堆PriorityQueue

让1点入队，以PII(距离，点号)的方式，因为PII类按first排序，所以让距离在前

当队非空

{

        取出队头，小顶堆保证取的是离源点最近的点

        标记该点

        用该点更新到其他点的最短距离，未标记的入队
}

return dist[n]

import java.util.*;

public class Text //主类 
{
	static int N=2025,M=N*N;
	static int[] h=new int[N],ne=new int[M],e=new int[M],w=new int[M]; 
	static int[] st=new int[N];
	static int[] dist=new int[N];
	static int idx;
	
	public static int gcd(int a,int b)
	{
		return b!=0? gcd(b,a%b):a;
	}
	
	public static void add(int a,int b,int t)
	{
		e[idx]=b;w[idx]=t;ne[idx]=h[a];h[a]=idx++;
	}
	
	public static int dijkstra()
	{
		Arrays.fill(dist,0x3f3f3f3f);
		dist[1]=0;
		PriorityQueue q=new PriorityQueue<>(); //小顶堆
		q.offer(new PII(0,1)); //按first排序 距离在前
		
		while(!q.isEmpty())
		{
			PII t=q.poll();
			int p=t.y;
			int d=t.x;
			
			if(st[p]==1) continue;
			st[p]=1;
			
			for(int i=h[p];i!=-1;i=ne[i])
			{
				int j=e[i];
				if(dist[j]>d+w[i])
				{
					dist[j]=d+w[i];
					q.offer(new PII(dist[j],j));
				}
			}
		}
		
		return dist[2021];
	}
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		Arrays.fill(h,-1);
		
		for(int i=1;i<=2021;i++)
			for(int j=1;j<=2021;j++)
				if(Math.abs(i-j)<=21)
				{
					int t=i*j/gcd(i,j);
					add(i,j,t); add(j,i,t);
				}
		int res=dijkstra();
		System.out.print(res);
	}
}

class PII implements Comparable
{
	int x,y;
	PII(int x,int y)
	{
		this.x=x;
		this.y=y;
	}
	public int compareTo(PII o)
	{
		return Integer.compare(x,o.x);
	}
}

3、spfa求最短路

模板：

用邻接表存 dist=0x3f   dist[1]=0  st[1]=1

st[]用于标记已在队列中的节点

当队非空

{

        取出队头，标记取消

        遍历与该点邻接的点，更新该点到起点的最短距离

        如果该点未标记，则标记入队

}

return dist[n]

import java.util.*;

public class Text //主类 
{
	static int N=2025,M=N*N;
	static int[] h=new int[N],ne=new int[M],e=new int[M],w=new int[M]; 
	static int[] st=new int[N];
	static int[] dist=new int[N];
	static int idx;
	
	public static int gcd(int a,int b)
	{
		return b!=0? gcd(b,a%b):a;
	}
	
	public static void add(int a,int b,int t)
	{
		e[idx]=b;w[idx]=t;ne[idx]=h[a];h[a]=idx++;
	}
	
	public static int spfa()
	{
		Arrays.fill(dist,0x3f3f3f3f);
		dist[1]=0;
		Queue q=new LinkedList<>();
		q.offer(1);
		st[1]=1;
		
		while(!q.isEmpty())
		{
			int t=q.poll();
			
			st[t]=0;
			
			for(int i=h[t];i!=-1;i=ne[i])
			{
				int j=e[i];
				if(dist[j]>dist[t]+w[i])
				{
					dist[j]=dist[t]+w[i];
					if(st[j]==0)
					{
						st[j]=1;
						q.offer(j);
					}
				}
			}
		}
		
		return dist[2021];
	}
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		Arrays.fill(h,-1);
		
		for(int i=1;i<=2021;i++)
			for(int j=1;j<=2021;j++)
				if(Math.abs(i-j)<=21)
				{
					int t=i*j/gcd(i,j);
					add(i,j,t); add(j,i,t);
				}
		int res=spfa();
		System.out.print(res);
	}
}

class PII implements Comparable
{
	int x,y;
	PII(int x,int y)
	{
		this.x=x;
		this.y=y;
	}
	public int compareTo(PII o)
	{
		return Integer.compare(x,o.x);
	}
}

F.时间显示 - 模拟

题目：

import java.util.*;

public class Main //主类 
{
	static int N=2025,M=N*N;
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		long n=sc.nextLong();
		long s=n/1000;
		
		long hh=s/3600%24;
		long mm=s/60%60;
		long ss=s%60;
		System.out.printf("%02d:%02d:%02d",hh,mm,ss);
	}
}

 

G.最少砝码 - 数学 + 找规律

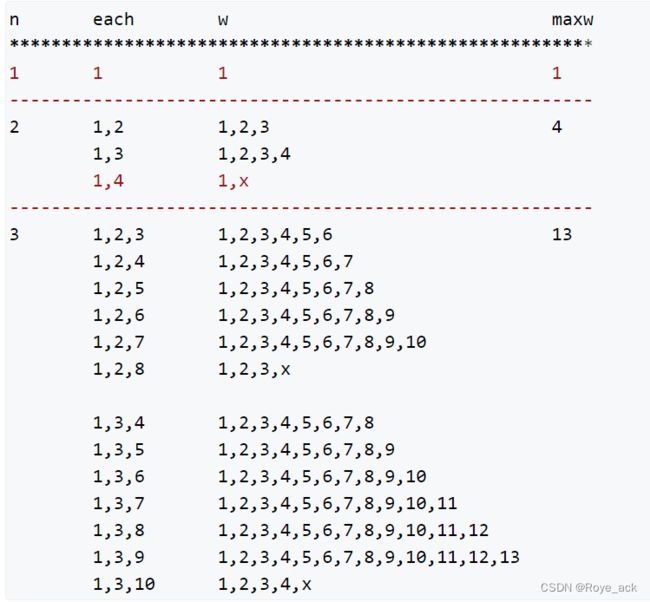
思路：

根据上述规律可知：

当选x个砝码时，f(x)为能称的最大重量，f(x)=f(x−1)∗3+1

import java.util.*;

public class Main //主类 
{
	static int N=2025,M=N*N;
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		long n=sc.nextLong();
		int res=1,cnt=1;
		while(true)
		{
			if(res>=n) break;
			res=res*3+1;
			cnt++;
		}
		System.out.print(cnt);
	}
}

 

H.杨辉三角形 - 组合数+二分

题目：

1、暴力40%

思路：

暴力枚举1000行，赚40分！ 

import java.util.*;

public class Main //主类 
{
	static int N=5000;
	static long[][] g=new long[N][N];
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		long n=sc.nextLong();
		long cnt=0;
		boolean f=false;
	
		for(int i=1;i<=5000;i++)
		{
			for(int j=1;j<=i;j++)
			{
				if(j==1||j==i) g[i][j]=1;
				else g[i][j]=g[i-1][j-1]+g[i-1][j];
				cnt++;
				if(g[i][j]==n)
				{
					f=true;
					break;
				}
			}
			if(f) break;
		}
		System.out.print(cnt);
	}
}

2、找规律+二分+组合数  100%

思路：

组合数和杨辉三角：第i行第j列的数都是组合数C(i, j) （i，j从0开始）

由于杨辉三角左右对称，又由于找第一次出现，因此一定在左边，右边可以直接删掉

                                     1      ---> C(0, 0)--第0斜行
                            1 
                      1             2     ---> C(2, 1)--第1斜行
                1          3                                               ---> C(2n, n)
          1          4             6     ---> C(4, 2)--第2斜行
     1         5          10
1        6         15           20    ---> C(6, 3)--第3斜行

测试发现C(33,15)>1e9，因此枚举前15斜行即可

性质：
        1. 每一斜行从上到下递增
         2. 每一横行从中间到两边依次递减

因此我们直接从中间对称轴倒序二分找起即可

C(r，k)对应的顺序值 = r*(r+1)/2+k+1

前面有r行，前面数总和为(r+1)*r/2，再加上它在这一行的位置k+1

二分：l=2k，r=max(n,l)

第k斜行的起始点为2k

右端点不能比左端点小，否则当n=1时会有问题

为什么倒序枚举斜行？

因为第1斜行是2~1e9，在第二斜行能找到这个数，但行数在下边，并不是第一个找到

import java.util.*;

public class Main //主类 
{
	static int N=10000;
	static int n;
	
	public static long C(int a,int b)
	{
		long res=1;
		for(int i=a,j=1;j<=b;i--,j++)
		{
			res=res*i/j;
			if(res>n) return res;
		}
		return res;
	}
	
	public static boolean check(int k)
	{
		int l=2*k,r=Math.max(n,l);
		while(l>1;
			if(C(mid,k)>=n) r=mid;
			else l=mid+1;
		}
		if(C(r,k)==n)
		{
			System.out.print(1l*(r+1)*r/2+k+1);
			return true;
		}
		return false;
	}
	
	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		
		n=sc.nextInt();
		//从第16斜行倒序枚举
		for(int k=16;;k--)
			if(check(k)) break;
	}
}