LeetCode 热题 HOT 100
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd" 输出:"bb"
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
题解:
(1)暴力破解法
思路:列举字符串所有的子串,判断是否为回文数,在返回其中最大的一个
实现代码:
class Solution:
def longestPalindrome(self, s: str) -> str:
def isHuiWenStr(subStr:str):#判断当前子串是不是回文字符
start = 0
end = len(subStr) - 1
while(start < end):
if(subStr[start] != subStr[end]):
return False
start = start + 1
end = end - 1
return True
if(len(s) < 2):
return s
maxLen = 1#记录最大回文字符长度
begin = 0#记录最大回文字符的起点
for i in range(len(s)-1):
for j in range(i + 1, len(s)):
if((j - i + 1) > maxLen and isHuiWenStr(s[i:j+1])):
maxLen = j - i + 1
begin = i
return s[begin:begin + maxLen](2)动态规划方法
参考:如何求一个字符串最长的回文子串 三种方法 思路详解_最长回文子串_lcy真的帅的博客-CSDN博客
136. 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1
示例 2 :
输入:nums = [4,1,2,1,2] 输出:4
示例 3 :
输入:nums = [1] 输出:1
题解:
二进制异或 异或规则:不同则为1,相同则为0。0^a=a, a^a=0. 如果数组为{1,2,2},如1^2,0001^0010异或之后则为0011,如果再^2,则为0011^0010,可得0001,即1。以此类推,最后剩下的就是只出现一次的数。
实现代码:
class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
for i in range(len(nums)):
res = res ^ nums[i]
return res287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2] 输出:2
示例 2:
输入:nums = [3,1,3,4,2] 输出:3
思想:
二进制异或 异或规则:不同则为1,相同则为0。0^a=a, a^a=0,就在异或的时候我们可以自由移动两个数字进行异或。
实现代码:
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
nums.sort()
for i in range(len(nums)):
if(nums[i] ^ nums[i+1] == 0):
return nums[i]
break
剑指 Offer II 070. 排序数组中只出现一次的数字
给定一个只包含整数的有序数组 nums ,每个元素都会出现两次,唯有一个数只会出现一次,请找出这个唯一的数字。
你设计的解决方案必须满足 O(log n) 时间复杂度和 O(1) 空间复杂度。
示例 1:
输入: nums = [1,1,2,3,3,4,4,8,8] 输出: 2
示例 2:
输入: nums = [3,3,7,7,10,11,11] 输出: 10
实现代码:
(1)异或法
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
#异或法
ans = 0
for i in range(len(nums)):
ans = ans ^ nums[i]
return ans(2)二分法
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
#异或法
# ans = 0
# for i in range(len(nums)):
# ans = ans ^ nums[i]
# return ans
l, r = 0, len(nums) - 1
while(l < r):
mid = l + (r - l) // 2
if(nums[mid] == nums[mid^1]):#mid^1表示mid左边或者右边的数
l = mid + 1
else:
r = mid
return nums[l]
参考: 力扣
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
题解:
(1)暴力解法(超时)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
maxProfit = 0
for i in range(len(prices)-1):
for j in range(i + 1, len(prices)):
if(prices[j] - prices[i] > maxProfit):
maxProfit = prices[j] - prices[i]
return maxProfit(2)动态规划
写法一:
股票问题一共有六道:买卖股票的最佳时机(1,2,3,4)、含冷冻期、含手续费。本题是第一道,属于入门题目。
股票问题的方法就是 动态规划,因为它包含了重叠子问题,即买卖股票的最佳时机是由之前买或不买的状态决定的,而之前买或不买又由更早的状态决定的...
遍历一遍数组,计算每次 到当天为止 的最小股票价格和最大利润。
实现代码:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# maxProfit = 0
# for i in range(len(prices)-1):
# for j in range(i + 1, len(prices)):
# if(prices[j] - prices[i] > maxProfit):
# maxProfit = prices[j] -prices[i]
# return maxProfit
minPrice = float('inf')#记录股票当天的最低价
maxProfit = 0#股票的最大利润
for i in range(len(prices)):
minPrice = min(prices[i], minPrice)
maxProfit = max(maxProfit, prices[i] - minPrice)#当前股价-之前最小股价就是当天的最大利润
return maxProfit
复杂度分析
时间复杂度:O(n),遍历了一遍数组。
空间复杂度:O(1),使用了有限的变量。
写法二:力扣
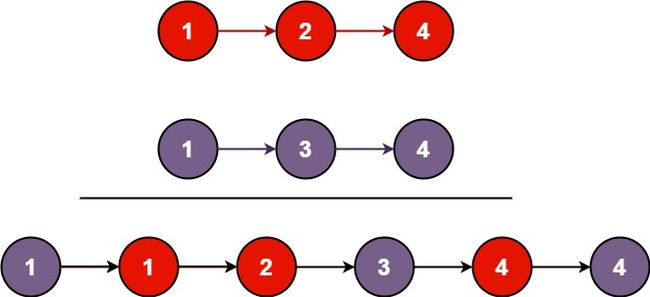
21. 合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = [] 输出:[]
示例 3:
输入:l1 = [], l2 = [0] 输出:[0]
提示:
- 两个链表的节点数目范围是
[0, 50] -100 <= Node.val <= 100l1和l2均按 非递减顺序 排列
实现代码:
这里list指向的是当前链表的头部的指针,list.next指向的是当前链表的下个元素:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
if(list1 is None):
return list2
elif(list2 is None):
return list1
elif(list1.val < list2.val):
list1.next = self.mergeTwoLists(list1.next, list2)
return list1
else:
list2.next = self.mergeTwoLists(list1, list2.next)
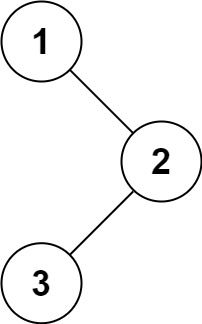
return list294. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1] 实现代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if(not root):
return []
return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
二叉树前中后序遍历递归版模板:
(1)写法一:
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
# 前序递归
return [root.val] + self.preorderTraversal(root.left) + self.preorderTraversal(root.right)
# # 中序递归
# return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
# # 后序递归
# return self.postorderTraversal(root.left) + self.postorderTraversal(root.right) + [root.val]
(2)写法二:
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
def dfs(cur):
if not cur:
return
# 前序递归
res.append(cur.val)
dfs(cur.left)
dfs(cur.right)
# # 中序递归
# dfs(cur.left)
# res.append(cur.val)
# dfs(cur.right)
# # 后序递归
# dfs(cur.left)
# dfs(cur.right)
# res.append(cur.val)
res = []
dfs(root)
return res
参考:力扣
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
思路:力扣
实现代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if(not root):
return []
cur, res = [root], []#cur表示当前层的节点,res存储最终的结果
while(cur):
lay, layval = [], []#lay表示某一层的节点,layval表示该层的所有节点值
for node in cur:#把同一层的节点放入lay
layval.append(node.val)
if(node.left):
lay.append(node.left)
if(node.right):
lay.append(node.right)
cur = lay
res.append(layval)
return res104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
思路:
求一棵二叉树的深度更简洁的写法:
int getHeight(node *root) {
return root==NULL ? 0 : max(getHeight(root->left), getHeight(root->right)) + 1
}实现代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
return 0 if(root == None) else (max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1)
# return root == None ? 0 : (max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1)
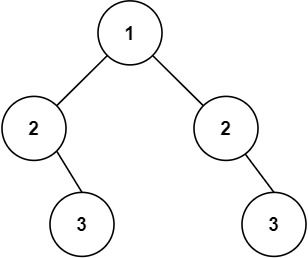
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false
思路:
对称二叉树的判定条件是: 左子树的左孩子 == 右子树的右孩子 and 左子树的右孩子 == 右子树的左孩子.
对于递归的终止条件:
当两个节点都为空,进入下一循环;
左右两个节点一个为空,一个不为空,一定不对称返回False;
左右两个节点都不为空,值不相等,一定不对称返回False.
实现代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
#开始递归
if(root is None):
return True
return self.isSameTree(root.left, root.right)#递归遍历左右子树
def isSameTree(self, left: TreeNode,right: TreeNode):
#递归的终止条件是两个节点都为空
#或左右有任意一个不为空,一定不对称
#两个节点的值不相等
if(left is None and right is None):
return True
if((left is None and right) or (left and right is None)):
return False
if(left.val != right.val):
return False
return self.isSameTree(left.left, right.right) and self.isSameTree(left.right, right.left)
参考:力扣
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = "" 输出:[]
示例 3:
输入:digits = "2" 输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
思路:
DFS回溯的动画显示:
实现代码:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if(len(digits) == 0):
return []
phoneMap = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz",
}
res = [] #初始化返回结果数组
temp = [] #初始化过渡数组
def backtrack(index:int):#定义递归回溯函数
#如果此时递归到了字符串中最后一个数字,则表示第一层深度搜索结束,将结果存储起来
if(index == len(digits)):
res.append(''.join(temp))#注意一下这边存储的时候要把多个字符串组合成一个字符串,利用
#join函数,这边还要注意的是后面会把tmp中的最上面字符弹出,这边利用join函数也同时避免
#了tmp弹出时影响res的目的,不然全部返回空字符串
else: #如果这个时候没搜索到最后一层,则
for i in phoneMap[digits[index]]:#逐个遍历当前数字对应的字母
temp.append(i)#将这个字母加到tmp中
#因为要把下一个数字对应的字母继续加进去,所以这边index + 1,函数传递下一个位置
backtrack(index + 1)
temp.pop()#因为还需要把最后一个数字的字母逐个加进去,所以这边要把最后一个弹出,
#因为上一行的 backtrack函数遇到结束条件,才回向下执行,所以这边已经完成一次深度的搜索,此时要把最后一个字母弹出,实现下一轮遍历
backtrack(0)#首先执行index = 0,因为都是从第一个字母开始组合
return res
参考:力扣
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
思想:
实现代码:
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
res = []
intervals.sort()
start, end = intervals[0]#区间的左右端点
for i in intervals:
if(i[0] > end):#i[0]表示当前的区间的左区间,i[0] > end标识此处断开
res.append([start, end])
start = i[0]
end = max(end, i[1])#i[1]表示当前的区间的右区间,i[0] < end标识此处未断开
res.append([start, end])
return res
参考:力扣
435. 无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
提示:
1 <= intervals.length <= 105intervals[i].length == 2-5 * 104 <= starti < endi <= 5 * 104
算法思想:
首先对区间集合按照左边界和右边界的大小升序排序。 两个准则: 1)由于区间集合经过排序,所以判断一个区间是否移除只需要参考它左边的区间; 2)对于有重叠的区间,优先选择右区间end更小的区间,移除end较大的区间(贪心思想,减小与后面区间重叠的可能) 总共的三种重叠区间情况如下:
对于有重叠的情况,保留右区间更小的,删除右区间更大的,这里只需要遇到重叠的区间,删除区间数加1,同时更新保留下的区间。
实现代码:
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
intervals.sort()
ans = 0
#对于有重叠的区间,优先选择右区间end更小的区间,移除end较大的区间(贪心思想,减小与后面区间重叠的可能)
for i in range(1, len(intervals)):
if(intervals[i][0] < intervals[i-1][1]):#两个区间有交集
ans += 1
intervals[i][1] = min(intervals[i][1], intervals[i-1][1])
#对于有重叠的情况,保留右区间更小的,删除右区间更大的,这样可以减少大区间与后面重叠的可能性
#这里只需要遇到重叠的区间,删除区间数加1,同时更新保留下的区间
# if(intervals[i][1] > intervals[i-1][1]):
# intervals[i] = intervals[i-1]
return ans
参考:力扣
455. 分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。 虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。 所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3] 输出: 2 解释: 你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。 你拥有的饼干数量和尺寸都足以让所有孩子满足。 所以你应该输出2.
提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
思想:
既然我们想让更多的孩子分食到饼干,那么最优的方案当然是从吃得少的人开始分配。 将孩子的胃口和饼干都按照升序排序。之后依次遍历,看多少个孩子能分得饼干即可。
这么做的时间复杂度是O(m+n)
实现代码:
class Solution:
def findContentChildren(self, g: List[int], s: List[int]) -> int:
ans = 0
g.sort()
s.sort()
j = 0
for i in range(len(g)):
while(j < len(s)):
if(g[i] <= s[j]):
ans += 1
j += 1
break
else:
j += 1
return ans参考: 力扣
452. 用最少数量的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:气球可以用2支箭来爆破: -在x = 6处射出箭,击破气球[2,8]和[1,6]。 -在x = 11处发射箭,击破气球[10,16]和[7,12]。
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]] 输出:4 解释:每个气球需要射出一支箭,总共需要4支箭。
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2 解释:气球可以用2支箭来爆破: - 在x = 2处发射箭,击破气球[1,2]和[2,3]。 - 在x = 4处射出箭,击破气球[3,4]和[4,5]。
提示:
1 <= points.length <= 105points[i].length == 2-231 <= xstart < xend <= 231 - 1
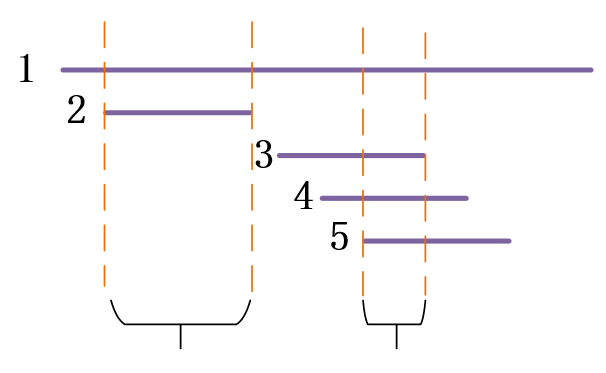
思想:
这个题打眼一看都知道思路,排序后尽可能找到重叠区域多的
主要有一个地方想不明白,假设按顺序两个气球重叠,他们没重叠的部分怎么就知道不能与其他的位置重叠更多呢 这里其实很简单,假设五个气球所在区间如下:
看起来1与345有着更大的重叠,一箭可以射穿四个气球,但其实每一箭都是射穿其他几个气球后射穿了1号气球。也就是说都是两根箭,1到底是被哪根箭射穿不重要,局部最优可以保证是最少箭数量即可。
想通这个问题后面只需要判断,排序后的两根箭是否重叠,即i-1的右端点是否小于i的左端点(注意相等的时候也算重叠),重叠则更新i的右端点为min(i-1的右,i的右)。 另外,需要注意起始箭从1开始。
实现代码:
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
if(len(points) == 0):
return 0
points.sort()
ans = 1 #points 不为空至少需要一支箭
#弓箭的数量就相当于是非交叉区间的数量
for i in range(1, len(points)):
if(points[i][0] > points[i-1][1]):#区间没有交集,需要一只箭来射穿
ans += 1
else:
points[i][1] = min(points[i][1], points[i-1][1])
return ans
参考: 力扣
55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 3 * 1040 <= nums[i] <= 105
思想:
- 如果某一个作为 起跳点 的格子可以跳跃的距离是 3,那么表示后面 3 个格子都可以作为 起跳点
- 可以对每一个能作为 起跳点 的格子都尝试跳一次,把 能跳到最远的距离 不断更新
- 如果可以一直跳到最后,就成功了
实现代码:
class Solution:
def canJump(self, nums: List[int]) -> bool:
maxJump = 0
for i in range(len(nums)):
if(i > maxJump):#当跳跃之后还没当前下标位置远,则一定不可以到达最后的下标位置
return False
else:
maxJump = max(maxJump, i + nums[i])#不断更新能跳到最远的距离
return True参考:力扣
169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3] 输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2] 输出:2
实现代码:
class Solution:
def majorityElement(self, nums: List[int]) -> int:
res = [0] * (max(nums) + 1)
for i in range(len(nums)):#统计每个元素出现的次数并把它存在res里
res[nums[i]] += 1
for j in range(len(res)):
if(res[j] > int(len(nums) / 2)):
return j229. 多数元素 II
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
示例 1:
输入:nums = [3,2,3] 输出:[3]
示例 2:
输入:nums = [1] 输出:[1]
示例 3:
输入:nums = [1,2] 输出:[1,2]
思路:
这题于上面的区别在于:由于有负数需要存储,所以list的数据结构不行,可以换成字典序的(key:value)来存储每个元素出现的次数。
实现代码:
class Solution:
def majorityElement(self, nums: List[int]) -> List[int]:
res = {} # 存放每个元素出现的次数
finalRes = [] # 存放最终结果元素
for i in nums: # 统计每个元素出现的次数
if (i in res):
res[i] += 1
else:
res[i] = 1
for j in res.keys():#按key值遍历
if (res[j] > len(nums) // 3): #//表示向上取整
finalRes.append(j)
return finalRes
448. 找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例 1:
输入:nums = [4,3,2,7,8,2,3,1] 输出:[5,6]
示例 2:
输入:nums = [1,1] 输出:[2]
提示:
n == nums.length1 <= n <= 1051 <= nums[i] <= n
思想:
实现代码:注意这里不用set的话会超时
class Solution:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
nums_set = set(nums)
res = []
for i in range(1, len(nums)+1):
if(i not in nums_set):
res.append(i)
return res参考:力扣
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1] 输出:9
思路:
主要考察去重+排序+贪心
实现代码:
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
nums_set = list(set(nums))#去重
nums_set.sort()
if(len(nums_set) == 0):
return 0
res,tmp = 1, 1#最少一个字符
for i in range(1, len(nums_set)):#贪心
if(nums_set[i]-nums_set[i-1] == 1):
tmp += 1
else:
tmp = 1
res = max(res, tmp)#每次选择最长的那个子串
return res动态规划的写法:
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
#以下用dp来做
if(len(nums) == 0):
return 0
if(len(nums) == 1):
return 1
nums.sort()
dp = [1]*len(nums)#起码一个字符
for i in range(1, len(nums)):
if(nums[i-1] == nums[i]):
dp[i] = dp[i-1]
if(nums[i]-nums[i-1] == 1):
dp[i] = dp[i-1] + 1
return max(dp)
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
思路:0/1背包问题
力扣
实现代码:
class Solution:
def rob(self, nums: List[int]) -> int:
if(len(nums) == 0):
return 0
#以下用0/1背包问题来解决
dp = [0]*(len(nums)+1)
dp[0] = 0#包里啥也没有
dp[1] = nums[0]
for i in range(2, len(nums)+1):
dp[i] = max(dp[i-1], dp[i-2] + nums[i-1])
return dp[len(nums)]参考:动态规划之背包问题系列总结_动态规划背包问题实验总结_金州饿霸的博客-CSDN博客
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12 输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13 输出:2 解释:13 = 4 + 9
思想:力扣
这是一个完全背包问题
实现代码:
class Solution:
def numSquares(self, n: int) -> int:
#由于每个平方数使用不受限制,所以此题为完全背包题
max = int(pow(n, 1/2))#最大的那个平方数
dp = [float('inf')] * (n + 1)
dp[0] = 0
for i in range(1, max+1):
w = i * i
for j in range(w, n + 1):#空间优化的写法
dp[j] = min(dp[j], dp[j-w] + 1)
return dp[n]
参考:动态规划之背包问题系列总结_动态规划背包问题实验总结_金州饿霸的博客-CSDN博客
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11 输出:3 解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3 输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0 思想:力扣 实现代码:
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0 # 合法的初始化,其他 dp[j]均不合法
for i in range(len(coins)):
for j in range(coins[i], amount + 1):
dp[j] = min(dp[j], dp[j - coins[i]] + 1)
#当表的最后一个值dp[n]没有被填充就说明没有最小值满足条件,我们就返回0
return dp[amount] if dp[amount] != float('inf') else -1
518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5] 输出:4 解释:有四种方式可以凑成总金额: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2] 输出:0 解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10] 输出:1
思想:力扣
注意这里是组合总数,且不考虑组合硬币的顺序。
实现代码:
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0] * (amount + 1)
dp[0] = 1 # 合法的初始化:凑出金额0的组合只有一种,即不选任何硬币
for i in range(len(coins)):
for j in range(coins[i], amount + 1):
dp[j] = dp[j] + dp[j - coins[i]]
return dp[amount] 41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0] 输出:3
示例 2:
输入:nums = [3,4,-1,1] 输出:2
示例 3:
输入:nums = [7,8,9,11,12] 输出:1
思想:
实现代码:
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
#时间复杂度O(n)不合题意
# nums.sort()
# res = 1#初始化最小的正整数,它记录当前的最小的正整数
# for n in nums:
# if(n > res):
# break
# if(n == res):
# res += 1
# return res
#空间复杂度O(n)不合题意
# dic = {}
# for i in nums:
# if(i > 0):#所有大于0的元素都放进哈希表内
# dic.update({i:i})
# for j in range(1, len(dic) + 1):
# if(j not in dic):#判断key在不在dic中
# return j
# return len(dic) + 1
#原地哈希表法符合题意
#要找的数一定在 [1, N + 1],我们要找的数就在 [1, N + 1] 里,最后 N + 1 这个元素我们不用找
for i in range(len(nums)):
# 先判断这个数字是不是索引,然后判断这个数字是不是放在了正确的地方
while(nums[i] in range(1, len(nums) + 1) and nums[nums[i] - 1] != nums[i]):
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]#交换两个元素的值
for i in range(len(nums)):
if(i + 1 != nums[i]):
return i + 1
return len(nums) + 1参考:力扣
448. 找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例 1:
输入:nums = [4,3,2,7,8,2,3,1] 输出:[5,6]
示例 2:
输入:nums = [1,1] 输出:[2]
提示:
n == nums.length1 <= n <= 1051 <= nums[i] <= n
进阶:你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。
思想:
时间复杂度:O(N),这里 N是数组的长度;
空间复杂度:O(1),这里没有使用额外的空间,这里采用原地哈希的方法。
说明:同样的思路和技巧,可以解决「力扣」第 41 题:缺失的第一个正数。
实现代码:
class Solution:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
#此方法空间复杂度为O(n)不合题意
# nums_set = set(nums)
# res = []
# for i in range(1, len(nums)+1):
# if(i not in nums_set):
# res.append(i)
# return res
#原地哈希法
for i in range(len(nums)):
while(nums[nums[i] - 1] != nums[i]):
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
return [i + 1 for i, num in enumerate(nums) if num != i + 1]#这里i表示数组的下标, 表示数组的值参考:力扣
442. 数组中重复的数据
给你一个长度为 n 的整数数组 nums ,其中 nums 的所有整数都在范围 [1, n] 内,且每个整数出现 一次 或 两次 。请你找出所有出现 两次 的整数,并以数组形式返回。
你必须设计并实现一个时间复杂度为 O(n) 且仅使用常量额外空间的算法解决此问题。
示例 1:
输入:nums = [4,3,2,7,8,2,3,1] 输出:[2,3]
示例 2:
输入:nums = [1,1,2] 输出:[1]
示例 3:
输入:nums = [1] 输出:[]
提示:
n == nums.length1 <= n <= 1051 <= nums[i] <= nnums中的每个元素出现 一次 或 两次
思想:
主体思想还是同上面两题,采用原地哈希的方法来降低空间复杂度。
原地哈希模板代码:通过反复交换,把数值存放在比该数值小1的下标上,eg:nums[0]=1
for i in range(len(nums)):
while(nums[nums[i] - 1] != nums[i]):
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1] 实现代码:
class Solution:
def findDuplicates(self, nums: List[int]) -> List[int]:
#原地哈希法
for i in range(len(nums)):
while(nums[nums[i] - 1] != nums[i]):
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
return [num for i, num in enumerate(nums) if num != i + 1]#这里i表示数组的下标, 表示数组的值num参考: 力扣
217. 存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1] 输出:true
示例 2:
输入:nums = [1,2,3,4] 输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2] 输出:true
思想:
遍历一遍数组,将结果采用哈希表存起来,一个key需要对应多个value,当key对应的value结果list长度>=2则输出true,否则输出false。
这里注意:python字典序如何一键赋多值
for i in range(len(nums)):
dic.setdefault(nums[i],[]).append(i)#字典一键赋多值实现代码:
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
dic = {}
for i in range(len(nums)):
dic.setdefault(nums[i],[]).append(i)#字典一键赋多值
for key, v in dic.items():
if(len(v) >= 2):
return True
return False219. 存在重复元素 II
给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,1], k = 3 输出:true
示例 2:
输入:nums = [1,0,1,1], k = 1 输出:true
示例 3:
输入:nums = [1,2,3,1,2,3], k = 2 输出:false
思想:
hash表一值对应多个value
实现代码:
class Solution:
def containsDuplicate(self, nums: List[int]) -> bool:
dic = {}
for i in range(len(nums)):
dic.setdefault(nums[i],[]).append(i)#字典一键赋多值
for key, v in dic.items():
if(len(v) >= 2):
return True
return False剑指 Offer 56 - I. 数组中数字出现的次数
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
示例 1:
输入:nums = [4,1,4,6] 输出:[1,6] 或 [6,1]
示例 2:
输入:nums = [1,2,10,4,1,4,3,3] 输出:[2,10] 或 [10,2]
实现代码:
class Solution:
def singleNumbers(self, nums: List[int]) -> List[int]:
dic = {}
for i in range(len(nums)):
dic.setdefault(nums[i],[]).append(i)#字典一键赋多值
return [k for k, v in dic.items() if(len(v) == 1)]剑指 Offer 56 - II. 数组中数字出现的次数 II
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
示例 1:
输入:nums = [3,4,3,3] 输出:4
示例 2:
输入:nums = [9,1,7,9,7,9,7] 输出:1
实现代码:
class Solution:
def singleNumber(self, nums: List[int]) -> int:
dic = {}
for i in range(len(nums)):
dic.setdefault(nums[i],[]).append(i)#字典一键赋多值
for k, v in dic.items():
if(len(v) == 1):
return k
剑指 Offer 39. 数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2
实现代码:
class Solution:
def majorityElement(self, nums: List[int]) -> int:
dic = {}
for i in range(len(nums)):
dic.setdefault(nums[i],[]).append(i)#字典一键赋多值
for k, v in dic.items():
if(len(v) > (len(nums) // 2)):
return k2150. 找出数组中的所有孤独数字
给你一个整数数组 nums 。如果数字 x 在数组中仅出现 一次 ,且没有 相邻 数字(即,x + 1 和 x - 1)出现在数组中,则认为数字 x 是 孤独数字 。
返回 nums 中的 所有 孤独数字。你可以按 任何顺序 返回答案。
示例 1:
输入:nums = [10,6,5,8] 输出:[10,8] 解释: - 10 是一个孤独数字,因为它只出现一次,并且 9 和 11 没有在 nums 中出现。 - 8 是一个孤独数字,因为它只出现一次,并且 7 和 9 没有在 nums 中出现。 - 5 不是一个孤独数字,因为 6 出现在 nums 中,反之亦然。 因此,nums 中的孤独数字是 [10, 8] 。 注意,也可以返回 [8, 10] 。
示例 2:
输入:nums = [1,3,5,3] 输出:[1,5] 解释: - 1 是一个孤独数字,因为它只出现一次,并且 0 和 2 没有在 nums 中出现。 - 5 是一个孤独数字,因为它只出现一次,并且 4 和 6 没有在 nums 中出现。 - 3 不是一个孤独数字,因为它出现两次。 因此,nums 中的孤独数字是 [1, 5] 。 注意,也可以返回 [5, 1] 。 思想:
实现代码:
这里注意python的Counter容器,它是每个元素出现次数的哈希表:
class Solution:
def findLonely(self, nums: List[int]) -> List[int]:
#超时
# dic = {}
# for i in range(len(nums)):
# dic.setdefault(nums[i], []).append(i)
# res = []
# for k, v in dic.items():
# if(len(v) == 1):
# if(k+1 not in nums and k-1 not in nums):
# res.append(k)
# return res
res = []
freq = Counter(nums) # 每个元素出现次数哈希表
print(freq)
for num in nums:
if freq[num-1] == 0 and freq[num+1] == 0 and freq[num] == 1:
res.append(num)
return res
参考:力扣
206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2] 输出:[2,1]
示例 3:
输入:head = [] 输出:[]
思想:
(1)首先摘下头节点,保存head之后的链表(这步很重要,防止断链)
(2)接着将head之后的链表指向结果链表的头部
(3)更新结果链表的头部res =head
(4)更新原链表的头节点head
实现代码:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
res = None#虚拟尾节点
#以下采用头插法建立链表
while(head):
temp = head.next#先保存head之后的链表(这步很重要,防止断链)
head.next = res #头插法
res = head
head = temp #更新head节点
# head.next, res, head = res, head, head.next #这一行与上面三行等价
return res可以利用python的多元赋值简化写法:
head.next, res, head = res, head, head.next #这一行与上面三行等价160. 相交链表
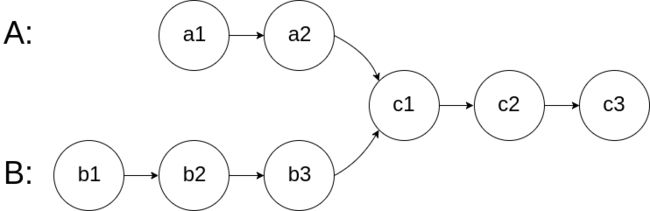
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA中节点数目为mlistB中节点数目为n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果
listA和listB没有交点,intersectVal为0 - 如果
listA和listB有交点,intersectVal == listA[skipA] == listB[skipB]
思想:
力扣
实现代码:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
#超时
# while(headA):
# moveB = headB#因为每次比较都是从头开始比较,需要提前存起来
# while(moveB):
# if(headA == moveB):
# return headA
# moveB = moveB.next
# headA = headA.next
# return None
res_A = set()
while(headA):
res_A.add(headA)
headA = headA.next
while(headB):
if(headB in res_A):
return headB
headB = headB.next
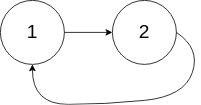
return None141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
思想:
用一个结果数组res来存储遍历过的节点值,然后每次看下一个节点的值是否在res里,如果在则证明有环,否则没有。
实现代码:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
res = []
while(head):
res.append(head)
if(head.next in res):#如果下一个节点在结果数组里则证明有环
return True
head = head.next#否则继续遍历链表
return False543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
思想:
实现代码:
参考:力扣