【数据结构与算法-动态规划系列经典例题汇总】
【数据结构与算法-动态规划系列经典例题汇总】
-
- 典例1、爬楼梯（easy）
- 典例2、打劫（medium）
- 典例3、最大字段和（easy）
- 典例4、找零钱（medium）
- 典例5、三角形（medium）
- 典例6、最长上升子序列（medium）
- 典例7、最小路径和（medium）
- 典例8、地下城游戏（hard）
动态规划概述：
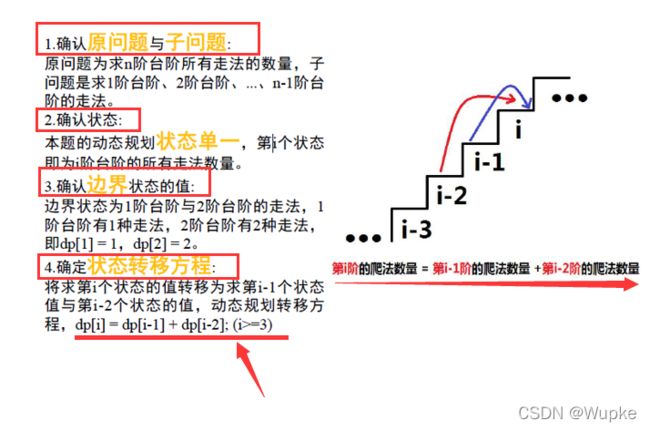
- 动态规划（dynamic programming）是运筹学的一个分支，是求解决策过程最优化的数学方法。它是最优化原理，利用各阶段之间的关系，逐个求解，最终求得全局最优解。在设计动态规划算法时，需要确认原问题与子问题、动态规划状态、边界状态结值、状态转移方程等关键要素。
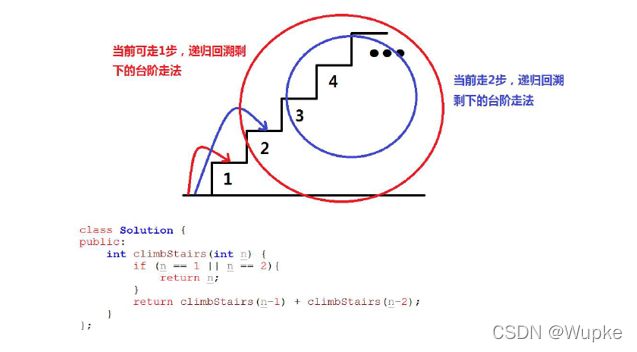
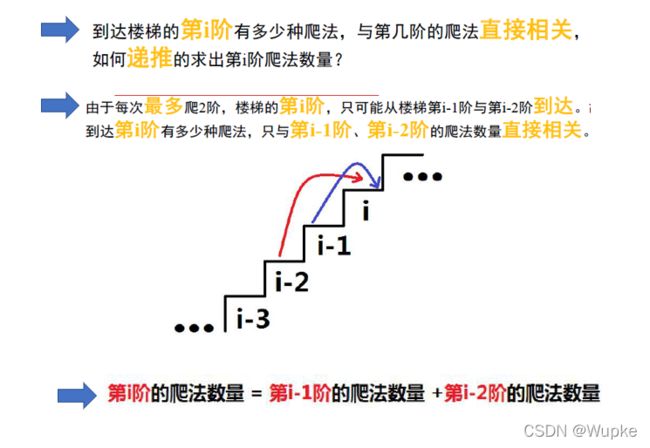
典例1、爬楼梯（easy）
-
题目描述：
-
思路：
-
暴力解法—回溯—>超时
-
改进：
-
算法流程：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution {
public:
int climbStairs(int n) {
std::vector<int> dp(n+3,0); // 防止数组越界，传入0？； 【dp】为 dynamic programming 简写
dp[1] = 1; // 边界值
dp[2] = 2;
for(int i=3;i<=n;i++){
dp[i] = dp[i-1] + dp[i-2]; // 动态转移方程（原问题与子问题的关系）
}
return dp[n];
}
};
// int main(){
// Solution solve;
// printf("%d\n",solve.climbStairs(3));
// return 0;
// }
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0] * (n + 1) # f(n) = f(n-1) + f(n-2),最后一次递归调用为 f(2) = f(1) + f(0)，边界就是 f(1) = 1，f(0) = 1。
dp[0]=1
dp[1]=1
for i in range(2,n+1):
dp[i]=dp[i-1]+dp[i-2]
return dp[n]
- 动态规划原理小结：
典例2、打劫（medium）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size()==0){return 0;} // 特殊情况
if(nums.size()==1){return nums[0];}
int n = nums.size();
vector<int> dp(n,0); // 声明变量存储对应的最优解数值,假定房间i的最优解为dp[i]
dp[0] = nums[0]; // 边界状态
dp[1] = max(nums[0],nums[1]);// 边界状态
for(int i = 2; i< n ; i++){
dp[i] = max(dp[i-1],dp[i-2]+nums[i]); // 状态转移方程
}
return dp[n-1];
}
};
// int main(){
// Solution solve; // 初始化类
// vector nums; // 初始化传入的数组
// nums.push_back(5);
// nums.push_back(2);
// nums.push_back(6);
// nums.push_back(3);
// nums.push_back(1);
// nums.push_back(7);
// printf("%d\n",solve.rob(nums)); // 调用函数，打印结果
// return 0;
// }
// 结果 ：18
python3
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n==0: return 0
if n==1: return nums[0]
dp = [0] * n # 设第 i 个房间的最优解 为 dp[i]
dp[0] = nums[0] # 边界值
dp[1] = max(nums[0],nums[1]) # 边界值
for i in range(2,len(nums)):
dp[i] = max(dp[i-1],dp[i-2]+nums[i]) # 动态转移方程，本质上是相邻的两个房间不能同取 （取i 不取 i）
return dp[n-1]
典例3、最大字段和（easy）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n,0); // 初始化数组，存储对应位置的最大值，先以 0 填充
dp[0] = nums[0]; // 边界状态
int max_res = dp[0]; // 初始化最大值
for(int i=1; i< n; i++){
dp[i] = max(dp[i-1]+nums[i],nums[i]); // 状态转移 （求第i个位置的连续最大值，本质上看之前的 i-1 个是正是负，正就带上，负就舍弃（拖累第i个的大小））
if(max_res < dp[i]){ // 如果之前的最大结果受到第 i 个数值存在的影响，则更新结果
max_res = dp[i];
}
}
return max_res;
}
};
// int main(){
// Solution solve; // 初始化类
// vector nums; // 初始化传入的数组
// nums.push_back(-2);
// nums.push_back(1);
// nums.push_back(-3);
// nums.push_back(4);
// nums.push_back(-1);
// nums.push_back(2);
// nums.push_back(1);
// nums.push_back(-5);
// nums.push_back(4);
// printf("%d\n",solve.maxSubArray(nums)); // 调用函数，打印结果
// return 0;
// }
// 结果 ：6
python 3
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
dp = [0] * n # 初始化数组，存储对应位置的最大值，先以 0 填充
dp[0] = nums[0] # 边界状态
max_res = dp[0] # 初始化最大值
for i in range(1,n):
dp[i] = max(dp[i-1]+nums[i],nums[i]) # 状态转移 （求第i个位置的连续最大值，本质上看之前的 i-1 个是正是负，正就带上，负就舍弃（拖累第i个的大小））
if max_res < dp[i]: #如果之前的最大结果受到第 i 个数值存在的影响，则更新结果
max_res = dp[i]
return max_res
典例4、找零钱（medium）
-
题目描述：
-
思路：
-
算法流程：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
cpp
// #include coins;
// coins.push_back(1);
// coins.push_back(2);
// coins.push_back(5);
// coins.push_back(7);
// coins.push_back(10);
// for (int i = 1; i<= 14; i++){
// printf("dp[%d] = %d\n", i, solve.coinChange(coins, i));
// }
// return 0;
// }
python3
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [0] + [10001] * (amount) # 初始化dp数组：因为钱币的数量一定不会超过amount；dp[j]代表含义：拼凑为j的钱数最少需要多少硬币
dp[0] = 0
for coin in coins: # 遍历所有的单面额钱数（对应的钱数只需1张）
for j in range(coin, amount + 1): # 从大于面额钱开始
dp[j] = min(dp[j], dp[j-coin] + 1) # 转移方程 ；当前填满容量j最少需要的硬币 = min( 之前填满容量j最少需要的硬币, 填满容量 j - coin 需要的硬币 + 1个当前硬币）
# return dp[amount] if dp[amount] != 10001 else -1 (三次运算符，等价于下面)
if dp[amount] != 10001:
return dp[amount]
else:
return -1 # 如果dp[amount]的值为10001没有变过，说明找不到硬币组合，返回-1
- python 中：
- float(“INF”) 表示为正无穷；
- float("-INF") 表示负无穷
- 所有数都比 -inf 大，所有数都比 +inf 小就可以了。
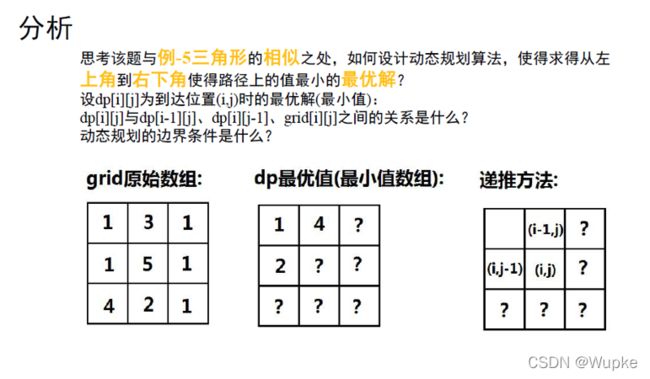
典例5、三角形（medium）
- 题目描述：
- 思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
// #include > triangle;
// int test[][10] = {{2}, {3, 4}, {6, 5, 7}, {4, 1, 8, 3}};
// for (int i = 0; i < 4; i++){
// triangle.push_back(std::vector());
// for (int j = 0; j < i + 1; j++){
// triangle[i].push_back(test[i][j]);
// }
// }
// Solution solve;
// printf("%d\n", solve.minimumTotal(triangle));
// return 0;
// }
python3
典例6、最长上升子序列（medium）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
// #include nums;
// for (int i = 0; i < 8; i++){
// nums.push_back(test[i]);
// }
// Solution solve;
// printf("%d\n", solve.lengthOfLIS(nums));
// return 0;
// }
python3
典例7、最小路径和（medium）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
// #include > grid;
// for (int i = 0; i < 3; i++){
// grid.push_back(std::vector());
// for (int j = 0; j < 3; j++){
// grid[i].push_back(test[i][j]);
// }
// }
// Solution solve;
// printf("%d\n", solve.minPathSum(grid));
// return 0;
// }
python3
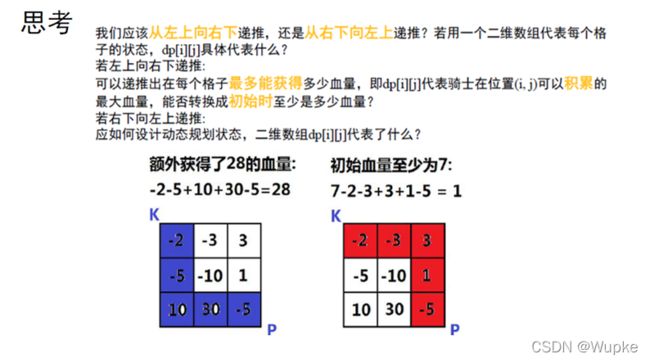
典例8、地下城游戏（hard）
-
题目描述：
-
思路：
-
LeetCode提交OJ测试链接:
-
OJ测试代码实现：
// class Solution {
// public:
// int calculateMinimumHP(vector>& dungeon) {
// }
// };
// #include > dungeon;
// for (int i = 0; i < 3; i++){
// dungeon.push_back(std::vector());
// for (int j = 0; j < 3; j++){
// dungeon[i].push_back(test[i][j]);
// }
// }
// Solution solve;
// printf("%d\n", solve.calculateMinimumHP(dungeon));
// return 0;
// }
python3