Distributed training of Deep Learning models with PyTorch

The motive of this article is to demonstrate the idea of Distributed Computing in the context of training large scale Deep Learning (DL) models. In particular, the article first presents the basic concepts of distributed computing and how it fits into the idea of Deep learning. Then it moves on to listing the standard requirements (hardware and software) for setting up an environment capable of handling distributed applications. Finally, to provide a hands-on experience, it demonstrates a specific distributed algorithm (namely Synchronous SGD) for training DL models from a theoretical as well as implementation perspective.

What is Distributed computing?

Distributed computing refers to the way of writing a program that makes use several distinct components connected over network. Typically, large scale computation is achieved by such an arrangement of computers capable of handling high density numeric computations in parallel. In distributed computing terminology, these computers are often referred to as nodes and a collection of such nodes form a cluster over the network. These nodes are usually connected via Ethernet, but other high-bandwidth networks are also used to take full advantage of the distributed architecture.

How does Deep learning benefit from distributed computing?

Although Neural Networks, the main workhorse of DL, has been in the literature from quite a while, nobody could utilise its full potential until recently. One of the primary reasons for the sudden boost in its popularity has something to with massive computational power, the very idea we are trying to address in this article. Deep learning requires training Deep neural networks (DNN) with massive number of parameters on a huge amount of data. Distributed computing is a perfect tool to take advantage of the modern hardware to its fullest. Here is the core idea:
A properly crafted distributed algorithm can:

• “Distribute” computation (forward and backward pass of a DL model) along with data across multiple nodes for coherent processing.
• It can then establish an effective “Synchronization” among the nodes to achieve consistency.

MPI: A distributed computing standard .

One more terminology you have to get used to — Message Passing Interface (MPI). MPI is the workhorse of almost all of distributed computing. MPI is an open standard that defines a set of rules on how the nodes will talk to each other over network and also a programming model/API. MPI is not a software or tool, it’s a specification. A group of individuals, organizations from academia and industry came forward in the summer of 1991 which eventually led to the creation of MPI Forum. The forum, with a consensus, crafted a syntactic and semantic specification of a library that is to be served as a guideline for different hardware vendors to come up with portable/ flexible/optimized implementations. Several hardware vendors have their own implementation of MPI — “OpenMPI”, “MPICH”, “MVAPICH”, “Intel MPI” and lot more.

In this tutorial, we are going to use Intel MPI as it is very performant and also optimized for Intel platforms. Original Intel MPI is a C library and very low level in nature.

The Setup

Proper setup of a distributed system is very important. Without proper hardware and network arrangements, it’s pretty much useless even if one has conceptual understanding of it’s programming model. Below are the key arrangements need to be made:

1. A set of nodes connected in a common network forming a cluster is typically required. It is recommended to have high-end servers as nodes and high-bandwidth network like InfiniBand.
2. Linux systems with user accounts of exact same name are required on all the nodes in the cluster.
3. Nodes must have password-less SSH connectivity among them. This is very crucial for seamless connectivity.
4. An MPI implementation must be installed. This tutorial focuses on Intel MPI only.
5. A common filesystem is required which is visible from all the nodes and the distributed applications must reside on it. Network Filesystem (NFS) is one way to achieve this.

Types of parallelization strategies

• Model parallelism
• Data parallelism

Model parallelism

Model parallelism refers to a model being logically split into several parts (i.e., some layers in one part and some in other), then placing them on different hardware/devices. Although placing the parts on different devices does have benefits in terms of execution time (asynchronous processing of data), it is usually employed to avoid memory constraints. Models with very large number of parameters, which are difficult fit into a single system due to high memory footprint, benefits from this type of strategy.

Data parallelism

Data parallelism, on the other hand, refers to processing multiple pieces (technically batches) of data through multiple replicas of the same network located on different hardware/devices. Unlike model parallelism, each replica may be an entire network and not just a part of it. This strategy, as you might have guessed, can scale up well with increasing amount of data. But, as the entire network has to reside on a single device, it cannot help models with high memory footprints. The illustration below should make it clear.

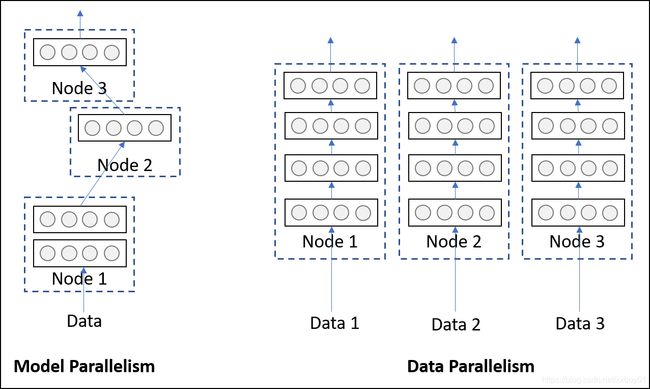
Practically, Data parallelism is more popular and frequently employed in large organizations for executing production quality DL training algorithms. So, in this tutorial, we will fix our focus on data parallelism.

The “torch.distributed” API

PyTorch offers a very elegant and easy-to-use API as an interface to the underlying MPI library written in C. PyTorch needs to be compiled from source and must be linked against the Intel MPI installed on the system. We will now see the basic usage of torch.distributed and how to execute it.

# filename 'ptdist.py'
import torch
import torch.distributed as dist
def main(rank, world):
    if rank == 0:
        x = torch.tensor([1., -1.]) # Tensor of interest
        dist.send(x, dst=1)
        print('Rank-0 has sent the following tensor to Rank-1')
        print(x)
    else:
        z = torch.tensor([0., 0.]) # A holder for recieving the tensor
        dist.recv(z, src=0)
        print('Rank-1 has recieved the following tensor from Rank-0')
        print(z)

if __name__ == '__main__':
    dist.init_process_group(backend='mpi')
    main(dist.get_rank(), dist.get_world_size())

Peer-to-peer communication . Executing the above code using mpiexec, a distributed process scheduler comes with any standard MPI implementation, results in:

cluster@miriad2a:~/nfs$ mpiexec -n 2 -ppn 1 -hosts miriad2a,miriad2b python ptdist.py
Rank-0 has sent the following tensor to Rank-1
tensor([ 1., -1.])
Rank-1 has recieved the following tensor from Rank-0
tensor([ 1., -1.])

1. The first line to be executed is dist.init_process_group(backend) which basically sets up the internal communication channel among the participating nodes. It takes an argument to specify which backend to use. As we are using MPI throughout, its backend=’mpi’ in our case. There are other backends as well (like “TCP”, “Gloo” and “NCCL”).
2. Two parameters need to be retrieved — the world size and rank.
   “World” refers to the collection of all nodes that have been specified in a particular context of mpiexec invocation (see the -hosts flag in mpiexec).
   “Rank” is a unique integer assigned by the MPI runtime to each of the processes. It starts from 0. The order in which they are specified in the argument of -hosts is used to assign the numbers. So, in this case, the process on node “miriad2a” will be assigned Rank 0 and “miriad2b” will be Rank 1.
3. x is a tensor that Rank 0 intends to send to Rank 1. It does so by dist.send(x, dst=1).
4. z is something that Rank 1 created before receiving the tensor. We need an already created tensor of same shape as a holder for receiving the incoming tensor. The values of z will eventually be replaced by the value of x.
5. Just like dist.send(…), the receiving counterpart is dist.recv(z, src=0) which receives the tensor into z.

Communication collectives

What we saw in the last section is an example of “peer-to-peer” communication where rank(s) send data to specific rank(s) in a given context. Although this is useful as it provides user with granular control over the communication, there exist other standard and frequently used patterns of communication called collectives. Below is the description of one particular collective (known as all-reduce) which is of interest to us in the context of Synchronous SGD algorithm.

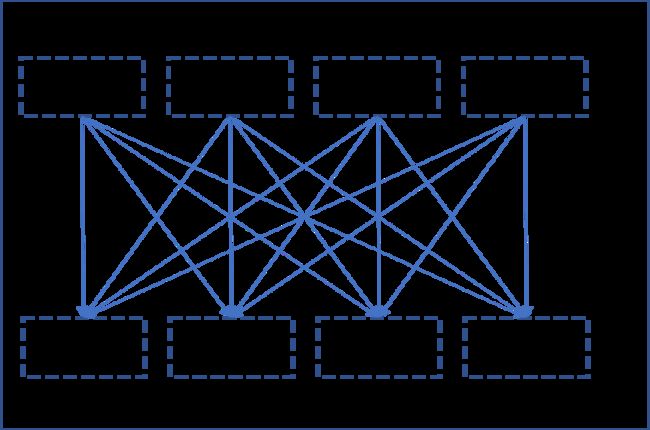
The “All-reduce” collective

All-reduce is a way of synchronized communication where a given reduction operation is operated on all the ranks and the reduced result is made available to all of them. The below figure illustrates the idea (uses summation as the reduction operation).

def main(rank, world):
    if rank == 0:
        x = torch.tensor([1.])
    elif rank == 1:
        x = torch.tensor([2.])
    elif rank == 2:
        x = torch.tensor([-3.])
    
    dist.all_reduce(x, op=dist.reduce_op.SUM)
    print('Rank {} has {}'.format(rank, x))

if __name__ == '__main__':
    dist.init_process_group(backend='mpi')
    main(dist.get_rank(), dist.get_world_size())

Basic usage of all-reduce collective in PyTorch When launched *in a world of 3*, results in

cluster@miriad2a:~/nfs$ mpiexec -n 3 -ppn 1 -hosts miriad2a,miriad2b,miriad2c python ptdist.py
Rank 1 has tensor([0.])
Rank 0 has tensor([0.])
Rank 2 has tensor([0.])

1. The if rank == … elif is a pattern we encounter again and again in distributed computing. In this case, it is used to create different tensors on different ranks.
2. They all execute an all-reduce together (see that dist.all_reduce(…) is outside if … elif block) with summation (dist.reduce_op.SUM) as reduction operation.
3. x from every rank is summed up and the summation is placed inside the same x of every rank.

Moving on to Deep learning

It is assumed that the reader is familiar with the standard Stochastic Gradient Descent (SGD) algorithm which is often used to train deep learning models. We will now see a variant of SGD (called Synchronous SGD) that makes use of the All-reduce collective to scale up. To lay the foundation, let’s start with the mathematical formulation of standard SGD.

$${\theta }_{new}={\theta }_{old}-\lambda {▽}_{\theta }\sum _{D}Loss(X,y)$$

where D is a set (mini-batch) of samples, θ is the set of all parameters, λ is the learning rate and Loss(X, y) is some loss function averaged over all samples in D.
The core trick that Synchronous SGD relies on is splitting the summation in the update rule over smaller subsets of (mini)batches. D is split into R number of subsets D₁, D₂, . . (preferably with same number of samples in each) such that

$$D=\bigcup _{r=1}^R{D}_r$$

Splitting the summation of standard SGD update formula leads to

$${\theta }_{new}={\theta }_{old}-\lambda {▽}_{\theta }\left[\sum _{D_1}Loss(X,y)+\sum _{D_2}Loss(X,y)+..+\sum _{D_R}Loss(X,y)\right]$$

Now, as the gradient operator is distributive over summation operator, we get

$${\theta }_{new}={\theta }_{old}-\lambda \left[{▽}_{\theta }\sum _{D_1}Loss(X,y)+{▽}_{\theta }\sum _{D_2}Loss(X,y)+..+{▽}_{\theta }\sum _{D_R}Loss(X,y)\right]$$

What do we get out of this?

Have a look at those individual gradient terms (inside square brackets) in the above equation. They can now be computed independently and summed up to get the original gradient without any loss/approximation. This is where the data parallelism comes into picture. Here is the whole story:

• Split the entire dataset into R equal chunks. The letter R is used to refer to Replica.
• Launch R processes/ranks using MPI and bind each process to one chunk of the dataset.
• Let each rank compute the gradient using a mini-batch (dᵣ) of size B from its own portion of data, i.e., rank r computes

$${▽}_{\theta }\sum _{d_r\in D_r}Loss(X,y)$$

• Sum up all the gradients of all the ranks and make the resulting gradient available to all of them to proceed further.

The last point is exactly the all-reduce algorithm. So, all-reduce must be executed every time all ranks have computed one gradient (on a mini-batch of size B) on their own portion of the dataset. A subtle point to note here is that summing up the gradients (on mini-batches of size B) from all R ranks leads to an effective batch size of
$$B_{effective}=R\times B$$
The following are the crucial parts of the implementation (the boilerplate codes are not shown)

model = LeNet()
# first synchronization of initial weights
sync_initial_weights(model, rank, world_size)

optimizer = optim.SGD(model.parameters(), lr=1e-3, momentum=0.85)

model.train()
for epoch in range(1, epochs + 1):
    for data, target in train_loader:
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        
        # The all-reduce on gradients
        sync_gradients(model, rank, world_size)
        
        optimizer.step()

def sync_initial_weights(model, rank, world_size):
    for param in model.parameters():
        if rank == 0:
            # Rank 0 is sending it's own weight
            # to all it's siblings (1 to world_size)
            for sibling in range(1, world_size):
                dist.send(param.data, dst=sibling)
        else:
            # Siblings must recieve the parameters
            dist.recv(param.data, src=0)

def sync_gradients(model, rank, world_size):
    for param in model.parameters():
        dist.all_reduce(param.grad.data, op=dist.reduce_op.SUM)

1. All R ranks create their own copy/replica of the model with random weights.
2. Individual replicas with random weights may lead to initial de-synchronization. It is preferable to synchronize the initial weights among all the replicas. The sync_initial_weights(…) routine does exactly that. Let any one of the ranks send its weights to its siblings and the siblings must receive them to initialize themselves with it.
3. Fetch a mini-batch (of size B) from the respective portion of a rank and compute forward and backward pass (gradient). Important point to note here as a part of the setup, is all processes/ranks should have its own portion of data visible (usually on its own hard-disk OR on a shared Filesystem).
4. Execute all-reduce collective on the gradients of each replica with summation as the reduction operation. The sync_gradients(…) routine does the gradient synchronization.
5. After gradients have been synchronized, every replica can execute a standard SGD update on its own weights independently. The optimizer.step() does the job as usual.

Now a question might arise, “How do we ensure that independent updates will remain in sync?”.
If we take a look at the update equation for the first update

$${\theta }_{firstupdate}\leftarrow {\theta }_{initial}-\lambda {▽}_{\theta }\sum _{D}Loss(X,y)$$

Point 2 & 4 above ensure that the initial weights and the gradients are synchronized individually. For obvious reason, a linear combination of them will also be in sync (λ is a constant). A similar logic holds for all consecutive updates.

Performance comparison

The biggest bottleneck for any distributed algorithm is the synchronization. Distributed algorithms are beneficial only if the synchronization time is significantly less than computation time. Let’s have a simple comparison between the standard and synchronous SGD to see when is the later one beneficial.

Definitions. Let’s assume the size of the entire dataset is N. Mini-batches of size B are processed by the network which takes time Tcomp. In the distributed case, time taken for all-reduce synchronization is Tsync. If there are R replicas, time taken for one epoch

For non-distributed (standard) SGD

$$T_{epoch}=(No.ofmini-batches)\times (Timetakenformini-bathc)\Rightarrow T_{epoch}=\frac{N}{B}\times T_{comp}$$

For Synchronous SGD

$$T_{epoch}=(No.ofmini-batches)\times (Timetakenformini-bathc)\Rightarrow T_{epoch}=\frac{N}{R\times B}\times (T_{comp}+T_{sync})$$

So, for the distributed setting to be significantly beneficial over non-distributed one, we need to have

$$\frac{N}{RB}(T_{comp}+T_{sync})<\frac{N}{B}{T}_{comp}$$

OR, equivalently

$$\frac{T_{sync}}{T_{comp}}<(R-1)$$

The three factors contributing to the above inequality can be tweaked to extract more and more benefit out of the distributed algorithm.

1. Tsync can be reduced by connecting the nodes over a high bandwidth (fast) network.
2. Tcomp can be increased by increasing batch size B.
3. R can be increased by connecting more nodes over the network and having more replicas.

Hopefully, the article was clear enough to convey the central idea of Distributed Computing in the context of Deep Learning. Although, Synchronous SGD is quite popular, there are other distributed algorithms which are also used quite frequently (like Asynchronous SGD and its variants). But, what is more important is to be able to think about deep learning methods in a parallel manner. Please realize that not all algorithms can be parallelized out-of-the-box; some require approximations to be made which break theoretical guarantees given by the original algorithms. It is up to the algorithm designer/implementer to tackle these approximations in an efficient way.