第十一届蓝桥杯国赛题目题解
试题 A: 美丽的 2
【问题描述】
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴。他很好奇,在公元 1 年到公元 2020 年(包含)中,有多少个年份的数位中包含数字 2?
题解
简单的遍历,只需要判断2在不在里面就完事儿了。
代码
ans = 0
for i in range(1, 2021):
i = str(i)
if '2' in i:
ans += 1
print(ans)
试题 B: 合数个数
【问题描述】
一个数如果除了 1 和自己还有其他约数,则称为一个合数。例如:1, 2, 3 不是合数,4, 6 是合数。请问从 1 到 2020 一共有多少个合数
题解
合数的本质就是寻找因数,遍历即可
代码
#方法一
def heshu(x):
for j in range(2, x):
for i in range(2, x):
if i * j == x:
return True
return False
ans = 0
for i in range(1,2021):
if heshu(i) is True:
ans += 1
print(ans)
#方法二(优化)
ans = 0
for i in range(4,2021): #2、3都是质数,可以直接4开始寻找
for j in range(2,i//2+1): #检测到i的一半就可以了
if i%j == 0:
ans += 1
break
print(ans)
试题 C: 阶乘约数
【问题描述】
定义阶乘 n! = 1 × 2 × 3 × · · · × n。请问 100! (100 的阶乘)有多少个约数。
题解
这道题需要一点数论基础,即一个数的约数的个数和其质因数个数相关,具体如下:
x = p 1 a 1 + p 2 a 2 + . . . + p k a k x = p_1 ^ {a_1 }+p_2^{a_2}+...+p_k^{a_k} x=p1a1+p2a2+...+pkak
约 数 个 数 = ( a 1 + 1 ) ∗ ( a 2 + 1 ) ∗ . . . ∗ ( a k + 1 ) 约数个数 = (a_1 + 1) *(a_2+1)*...*(a_k+1) 约数个数=(a1+1)∗(a2+1)∗...∗(ak+1)
其中 p 1 、 p 2 . . . p k p_1、p_2...p_k p1、p2...pk为质数,现在我们需要做的就是将1到100(其实是2到100,因为1没有质因数)分解质因数,然后统计每一个质因数的个数,然后应用上面的公式即可。
代码
primes,cnt = [0]*110,0
minp = [0]*110
st = [False]*110
def get_primes(n):
global cnt
for i in range(2,n+1):
if st[i] == False:
minp[i] = i
primes[cnt] = i
cnt += 1
j = 0
while primes[j]*i <=n:
t = primes[j]*i
st[t] = True
minp[t] = primes[j]
if i%primes[j]:
j += 1
else:
break
get_primes(100)
num = [0]*110
for i in range(2,101):
while i>1:
p = minp[i]
while i%p==0:
i //=p
num[p] += 1
res = 1
for i in range(1,101):
if num[i] != 0:
res *= (num[i]+1)
print(res)试题 D: 本质上升序列
【问题描述】
小蓝特别喜欢单调递增的事物。在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
题解
这道题的本质就是寻找递增序列,我们可以采用动态规划的方法来解决。所以我们先来了解一下动态规划。
所谓动态规划,最简单的就是我们的斐波那契数列,每一步的结果都可以由前面两步递推得到。即存在
Fibonacci[i] = Fibonacci[i-1] + Fibonacci[i-2]
这个公式提醒我们动态规划的两个重要条件,首先,我们需要知道第0个和第1个元素,这样这个公式才能往下继续递推;同时,我们需要知道针对一道题的递推关系式,这是保证题目能够存在后续解。所以,初始条件和递推公式在动态规划中显得十分重要。
以本题为例,本质上升序列是寻找每一个字母对应的不同子序列,我们采用的方式是利用固定每一个字母,然后依次搜索的方式。同时保存每一个搜索到的字符,最后再进行去重工作,计数。
按照以上思路,很明显是一个深度遍历(DFS)的过程。我们需要对每一个字符进行搜索。写出来后输入样例检验是没有问题的,但是当我们输入原题要求时就出现问题了——跑不出结果。仔细分析会发现,按照这个思路,搜索的时间复杂度是O(2^n),对于n=length=200的长度来说,实在是噩梦。更不要说递归调用函数的时间本来就很长。
于是我们思考优化我们的方案,基于一个朴素的认知,一般递归能够解决的问题都可以采用动态规划解决。所以,我们采用动态规划。
先考虑初始化,按照题意,每一个字母本身也是一个子序列,那么就是说每一个字母至少有一个子序列(如果字母不重复),所以我们初始化dp=[1]*n
再考虑递推公式,递推公式有两种可能,一是将每一个字母当作首字母,对其后面可能出现的字母进行检索;而是将每一个字母当作末字母进行检索。很明显,如果将每一个字母当作首字母,从第一个字母开始向后检索,那么对于第一个字母我们将检索(2^(n-1))次,也不满足我们的初始条件,这导致我们要修改初始条件,那么代码将没有普适性,也不利于递推公式的推导,所以不加以考虑,这种情况下应该考虑从后往前检索,同理,如果是将每一个字母当作末字母,我们应从前往后检索,这里为了方便,我们采用第二种方法。
我们首先看’l’,以’l’为末的字符串只有它本身,则为1,再看’a’,虽然它前面有一个字母,但是’l’的字典序列大于’a’,所以’a’也只有1,再看’n’,现是它本身,然后又’ln’、‘an’,则是3,即1+1+1=3,对于’q’来说,现是其本身,然后它字典序在’l’后面,所以’l’的所有可能都可以添加到q上,对于’a’、'n’也是同理,即1+1+3+1=6,其实到这里,我们可以发现这就像一个排列问题,只要空间位置和字典序某字母甲在乙后面,那么乙的所有可能就可以看作一个整体作用在甲的身上。所以,我们可以写出递推公式***if chr(甲)>chr(乙):–>L(甲)= L(甲) + L(乙)***。
当然我们还需要考虑一种情形,即某个字母甲在前面已经出现过,那么我们就可以先求得这个字母所有的可能组合,再减掉已经出现过的组合。综上,完整的递推公式是 if chr(甲)>chr(乙):–>L(甲1) = L(甲1) + L(乙) + L(丙) +……+L(终止) - (L(甲2)+L(甲3)+……+L(甲n))
找到初始条件和递推关系后,就可以写代码了。
代码
str1 = 'lanqiao'
n = len(str1)
dp = [1] * n
for i in range(n):
for j in range(i):
if str1[j] < str1[i]:
dp[i] += dp[j]
elif str1[i] == str1[j]:
dp[i] -= dp[j]
print(sum(dp))试题 E: 玩具蛇
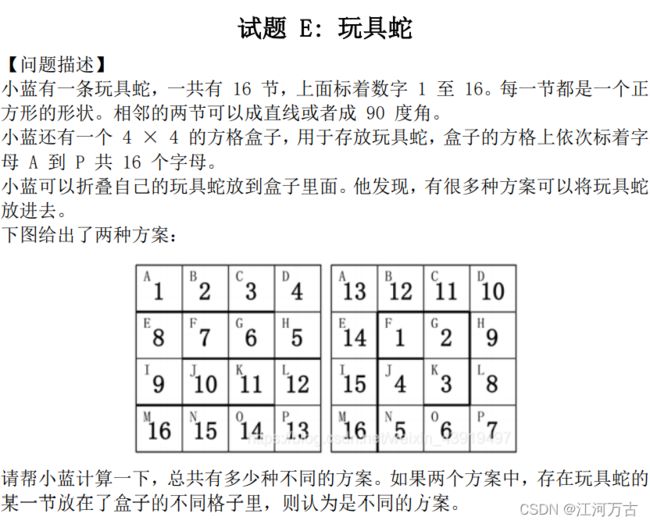
【问题描述】
题解
这是一个往固定格子里放置物品的问题,唯一的限制就是物品是连续的,摆放时又顺序限制。当然,这只是题目写出的限制,我们要找出题目隐含条件的限制。
为了方便,我们将问题看作一个人,在十六宫格中任选一格作为起始点,其可以上下左右移动,但不能经过已经走过的格子,问这个人有多少种方法走完十六宫格。我们记其所在位置是(x,y),每次移动记为。
那么第一个条件很明显,即,限制其不能离开十六宫格;第二个限制条件就是下一步的格子不能是已经走过的格子;而相比于前两个限制条件,第三个条件就没有那么容易想到——我们选择的行走方式一定要走完16个格子。
在弄清楚这三个条件之后,我们需要做的就是找出所有的行走方式,然后再与条件进行一一对照。即先遍历,再对照。按照这个思路,我们可以很轻易的想到回溯算法。
这里简单介绍一下回溯算法。
我们能够想到的最简单的回溯算法的应用就是树的结点的遍历,从根节点开始搜索,搜索到一个叶子节点后,记录并返回上一节点,再搜索该节点的其它子节点,搜索完之后再回溯到再上一个节点,重复以上操作,即递推,一直到遍历完所有节点,这就是我们常说的DFS。
回溯算法有几个鲜明的特点:一、需要对所有可能进行遍历,毫不客气地说,这是一种极为低效的算法。二、记忆化,将满足条件的可能进行记忆,防止重复。三、回溯算法能够解决的问题全部都可以化作“树”的形式。
同时,它的代码也有几个特点:一、for循环横向遍历,递归纵向遍历;二、实现形式一般都是递归;三、需要明确终止条件。
在大概了解回溯算法之后,我们来看题。
如果我从A点开始走,我可以建立一个如下的树
很明显,我们需要找到的是一个高度为16的树,但除去高为16之外,我们还要满足第二、第三个条件(在这个树里,第一个条件已经满足),利用这两个条件对树进行剪枝,剩下的所有高为16的树就是起点为A的所有的走法。同时,我们观察到A、D、M、P四个点完全对称,B、C、E、I、H、L、N、O八个点完全对称。、;F、J、G、K完全对称,即L = 4L(A) + 8L(B) + 4L(F)即可。
同时,我们观察这棵树,我们会发现一个小惊喜,由于回溯算法的记忆化,那么不满足第三个条件的走法无法达到高度16,也就是说,我们真正需要在代码里添加的条件其实只有第二个——不能重复行走。
现在,我们已经有了回溯条件,只需要找到终止条件即可,很明显,观察上面那棵树,终止条件是high = 16,每一次high = 16,ans+=1即可。
代码
ml = [[-1, 0], [0, -1], [1, 0], [0, 1]]
move = [[False, False, False, False],
[False, False, False, False],
[False, False, False, False],
[False, False, False, False]]
ans = 0
def DFS(x, y, step):
global ans
if step == 15:
ans += 1
return
move[x][y] = True
for i in range(4):
dx = x + ml[i][0]
dy = y + ml[i][1]
if dx>= 0 and dx < 4 and dy >= 0 and dy < 4:
if move[dx][dy] is False:
DFS(dx, dy, step+1)
move[x][y] = False
for i in range(4):
for j in range(4):
DFS(i, j, 0)
print(ans)试题 F: 天干地支
【问题描述】
题解
没什么好说的,算就完了
代码
t = ["","xin","ren","gui","jia","yi","bing","ding","wu","ji","geng"]
d = ["","you","xu","hai","zi","chou","yin","mao","chen","si","wu","wei","shen"]
n = int(input())
a,b = 1,1
for i in range(1,n+1):
if a>10:
a = a%10
if a%10 == 0:
a = 10
if b>12:
b = b%12
if b%12 == 0:
b = 12
a += 1
b += 1
print(t[a-1]+d[b-1])题解
其实这道题比较简单,只是需要思路上转一个弯就可以了。
首先n=s.length,如果n%k!=0,那直接return 1就可以了。
否则,以样例’aabbaa’,2为例,我们将其等分为’aab’,‘baa’,然后横向排列
a a b
------------------------------------------
b a a
##代码
k=int(input())
s=input()
d, x=[], []
s1=""
m, c=len(s)//k, 0
print(len(s))
if len(s)%k!=0:
print("1")
else:
for i in range(m):
for i1 in range(k):
s1+=s[i+i1*m]
d.append(s1)
s1=""
for i in d:
a=set(i)
for i1 in a:
x.append(i.count(i1))
c+=k-max(x)
x=[]
print(c)试题 H: 答疑
【问题描述】
有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。老师可以安排答疑的顺序,同学们要依次进入老师办公室答疑。一位同学答疑的过程如下:
1.首先进入办公室,编号为 i 的同学需要 si 毫秒的时间。
2.然后同学问问题老师解答,编号为 i 的同学需要 ai 毫秒的时间。
3.答疑完成后,同学很高兴,会在课程群里面发一条消息,需要的时间可以忽略。
4.最后同学收拾东西离开办公室,需要 ei 毫秒的时间。一般需要 10 秒、20 秒或 30 秒,即 ei 取值为 10000,20000 或 30000。
一位同学离开办公室后,紧接着下一位同学就可以进入办公室了。答疑从 0 时刻开始。老师想合理的安排答疑的顺序,使得同学们在课程群里面发消息的时刻之和最小
【输入格式】
输入第一行包含一个整数 n,表示同学的数量。接下来 n 行,描述每位同学的时间。其中第 i 行包含三个整数 si, ai, ei,意义如上所述。
【输出格式】
输出一个整数,表示同学们在课程群里面发消息的时刻之和最小是多少。
【样例输入】
3
10000 10000 10000
20000 50000 20000
30000 20000 30000
【样例输出】
280000
【样例说明】
按照 1, 3, 2 的顺序答疑,发消息的时间分别是 20000, 80000, 180000。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ n ≤ 20。
对于 60% 的评测用例,1 ≤ n ≤ 200。
对于所有评测用例,1 ≤ n ≤ 1000,1 ≤ si ≤ 60000,1 ≤ ai ≤ 1000000,ei ∈ {10000, 20000, 30000},即 ei 一定是 10000、20000、30000 之一。
题解
这是一道典型的读懂比写懂难的题,题目又臭又长,但其实题目并不难。我们可以轻易的知道:
所以,我们可以轻易的知道,只需要对所有的进行排序即可,如果大小相等,即按照从小到大排序即可。
代码
n = int(input())
timelist, sumlist = [], []
ci, res = 0, 0
for i in range(n):
each = [int(i) for i in input().split()]
timelist.append(each)
for i in range(n):
ci += timelist[i][2]
for i in range(n):
sum = 0
for j in timelist[i]:
sum += j
sumlist.append(sum)
sumlist.sort()
for i in sumlist:
res += n * i
n -= 1
print(res - ci)试题 I: 补给
【问题描述】
小蓝是一个直升飞机驾驶员,他负责给山区的 n 个村庄运送物资。每个月,他都要到每个村庄至少一次,可以多于一次,将村庄需要的物资运送过去。每个村庄都正好有一个直升机场,每两个村庄之间的路程都正好是村庄之间的直线距离。
由于直升机的油箱大小有限,小蓝单次飞行的距离不能超过 D。每个直升机场都有加油站,可以给直升机加满油。每个月,小蓝都是从总部出发,给各个村庄运送完物资后回到总部。如果方便,小蓝中途也可以经过总部来加油。
总部位于编号为 1 的村庄。请问,要完成一个月的任务,小蓝至少要飞行多长距离?
题解(狡辩)
由于时间紧,任务重,来不及看这道题,所以就没做,同学们自己加油(其实就是菜,不会,还懒)
试题 J: 蓝跳跳
【问题描述】
小蓝制作了一个机器人,取名为蓝跳跳,因为这个机器人走路的时候基本靠跳跃。
蓝跳跳可以跳着走,也可以掉头。蓝跳跳每步跳的距离都必须是整数,每步可以跳不超过 k 的长度。由于蓝跳跳的平衡性设计得不太好,如果连续两次都是跳跃,而且两次跳跃的距离都至少是 p,则蓝跳跳会摔倒,这是小蓝不愿意看到的。
小蓝接到一个特别的任务,要在一个长为 L 舞台上展示蓝跳跳。小蓝要控制蓝跳跳从舞台的左边走到右边,然后掉头,然后从右边走到左边,然后掉头,然后再从左边走到右边,然后掉头,再从右边走到左边,然后掉头,如此往复。为了让观者不至于太无趣,小蓝决定让蓝跳跳每次用不同的方式来走。小蓝将蓝跳跳每一步跳的距离记录下来,按顺序排成一列,显然这一列数每个都不超过 k 且和是 L。这样走一趟就会出来一列数。如果两列数的长度不同,或者两列数中存在一个位置数值不同,就认为是不同的方案。
请问蓝跳跳在不摔倒的前提下,有多少种不同的方案从舞台一边走到另一边。
【输入格式】
输入一行包含三个整数 k, p, L。
【输出格式】
输出一个整数,表示答案。答案可能很大,请输出答案除以 20201114 的余数。
【样例输入】
3 2 5
【样例输出】
9
【样例说明】
蓝跳跳有以下 9 种跳法:
1. 1+1+1+1+1
2. 1+1+1+2
3. 1+1+2+1
4. 1+2+1+1
5. 2+1+1+1
6. 2+1+2
7. 1+1+3
emsp; 8. 1+3+1
9. 3+1+1
【样例输入】
5 3 10
【样例输出】
397
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ p ≤ k ≤ 50,1 ≤ L ≤ 1000。
对于 60% 的评测用例,1 ≤ p ≤ k ≤ 50,1 ≤ L ≤ 109。
对于 80% 的评测用例,1 ≤ p ≤ k ≤ 200,1 ≤ L ≤ 1018。
对于所有评测用例,1 ≤ p ≤ k ≤ 1000,1 ≤ L ≤ 1018
题解
动态规划,但是规律不好发现,需要我们把所有的可能写出来进行分析,分析思路来自于CSDN博主@猪哥66的文章,这里就不再赘述
代码
if __name__ == '__main__':
# 输入 k p l,空格分隔
k, p, L = map(int, input("input k p L separated by one spaces:").split())
# 1、生成二维数组,0层存 第一步小于p的方案数,1层存 总方案数
# 最小数组长度
len = k + 1
dp = [[0 for e1 in range(2)] for e in range(len)]
# 赋值 L=0 的情况
dp[0][0] = 1
dp[0][1] = 1
i = 0 # 定义循环写入的角标
# L为总距离数
for l in range(1, L + 1): # l无用
# 循环改变数组列角标,取模
i = (i + 1) % len
# 临时值,用于将 第一步小于p的方案数 与
# 第一步大于等于p的方案数相加
sum = 0
# 2、开始计算 第一步小于p的方案数,存储在二维数组的0层
for j in range(1, p):
sum += (dp[(i - j) % len][1]) % 20201114
dp[i][0] = sum # 记录 第一步小于p的方案数
# 3、开始计算 第一步大于等于p的方案数
for o in range(p, k + 1):
# 之前sum已经是 第一步小于p的方案数
# 这里直接相加就等于总方案数啦
sum += dp[(i - o) % len][0] % 20201114
dp[i][1] = sum # 4、记录总方案数,存储在二维数组的1层
# 5、循环结束,直接获取对应角标的1层即是 总方案数
print((dp[i][1]) % 20201114)