图像分割(一)——Axial-DeepLab: Stand-Alone Axial-Attention for Panoptic Segmentation
Axial-DeepLab: Stand-Alone Axial-Attention for Panoptic Segmentation
- Abstract
- 1 Introduction
- Method
-
- Position-Sensitive Self-Attention
- Axial-Attention
纯transformer框架的全景分割
Abstract
卷积利用局部性来提高效率,但代价是丢失长范围上下文。自注意力通过非局部的相互作用来增强CNN。最近的研究证明,通过将注意力限制在局部区域来堆叠自注意力层来获得完全注意网络是可能的。在本文中,我们试图通过将二维自注意力分解为两个一维自注意力来消除这一限制。这降低了计算复杂度,并允许在更大甚至全局区域内进行注意。同时,我们还提出了一种位置敏感型的自注意力设计。两者结合在一起产生了位置敏感的轴向注意力层,这是一种新的构建块,可以堆叠起来形成用于图像分类和密集预测的轴向注意力模型。我们在四个大规模数据集上验证了我们的模型的有效性。特别是,我们的模型比ImageNet上现有的所有独立自注意力模型都要好。我们的Axial-DeepLab在COCO测试开发上比自下而上的最先进水平提高了2.8%的PQ。以前的最先进技术是通过我们的小变体实现的,它的参数效率是3.8倍,计算效率是27倍。Axis-DeepLab还在地图景观和城市景观上取得了最先进的结果。
1 Introduction
卷积是计算机视觉的核心构件。早期的算法使用卷积滤波来模糊图像、提取边缘或检测特征。与全连接模型相比,由于其效率和泛化能力,它在现代神经网络中得到了广泛的开发。卷积的成功主要来源于两个性质:平移等价性和局部性
- 平移等价性,虽然不是精确的,但很好地符合成像的性质,从而将模型推广到不同位置或不同大小的图像。
- 局部性,减少了参数计数和M-Adds. 然而,这使得对长程关系的建模具有挑战性。
大量文献讨论了卷积神经网络(CNNs)中长程相互作用的建模方法。有些采用空洞卷积,更大卷积核,图像金字塔。要么手工设计,要么通过算法搜索。另一类作品采用了注意力机制。注意力在语言建模、语音识别和神经字幕中显示其对远程交互进行建模的能力。自那以后,注意力已经扩展到视觉上,对图像分类、目标检测、语义分割、视频分类和对抗性防御给予了显著的提升。这些工作通过非局部性和长程注意力模块丰富了CNN。
最近,有人提出将注意力层堆叠为没有任何空间卷积的独立模型,并显示了有希望的结果。然而,单纯的注意力在计算上是昂贵的,尤其是在大的输入上。有人提出对注意力应用局部约束可以降低成本,并能够构建完全注意力模型。然而,局部约束限制了模型感受野,而感受野对于分割等任务至关重要,尤其是在高分辨率输入上。
在这项工作中,我们建议采用轴向注意,这不仅可以进行有效的计算,而且可以恢复独立注意模型中的大感受野。·
其核心思想是将二维注意力按高度和宽度轴顺序分解为两个一维注意力。它的效率使我们能够参与大范围的活动,并构建模型来学习远程甚至全局相互作用。此外,以前的大多数注意力模块都没有利用位置信息,这降低了注意力对位置依赖相互作用的建模能力,比如在多尺度的形状和目标,最近的作品引入了位置信息到注意力中,但以一种上下文无关的方式。在本文中,我们增加了位置项,使其与上下文相关,使我们的注意力对位置敏感,具有较小的成本。
我们的贡献有四个方面:
- 该方法首次尝试构建具有大或全局感受野的独立注意力模型。
- 提出了位置敏感注意层,它可以更好地利用位置信息,而不会增加太多的计算成本。
- 我们证明了轴向注意工作得很好,不仅作为一个独立的图像分类模型,而且作为全光分割、实例分割和分段分割的骨干。
- 我们的Axial-DeepLab在coco上比自下而上的最先进的方法有显著的改进,实现了与两阶段方法相当的性能。我们还在地图景观和城市景观上超过了以前的最先进的方法。
Method
我们首先正式介绍我们对位置敏感的自我注意机制。然后,我们讨论了如何将其应用于轴注意,以及如何使用轴关注层构建独立的Axial-ResNet和Axial-DeepLab.
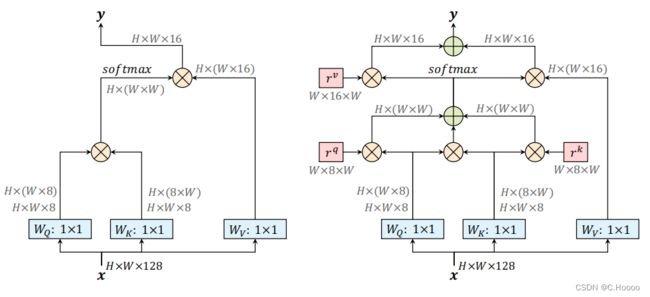
Position-Sensitive Self-Attention
自注意力机制通常被应用于视觉模型,作为增加CNN输出的附加机制。给定具有高度h, 宽度w和通道 d i n d_{in} din 的输入特征图 x ∈ R h × w × d i n \mathbf{x}\in \mathbb{R}^{h\times w\times d_{in}} x∈Rh×w×din ,位置 o = ( i , j ) o=(i,j) o=(i,j) 处的输出 y o ∈ R d o u t y_o\in \mathbb{R}^{d_{out}} yo∈Rdout 为
y o = ∑ p ∈ N softmax p ( q o T k p ) v p (1) y_{o}=\sum_{p \in \mathcal{N}} \operatorname{softmax}_{p}\left(q_{o}^{T} k_{p}\right) v_{p}\tag{1} yo=p∈N∑softmaxp(qoTkp)vp(1)这里 N \mathcal{N} N是整个位置点阵, s o f t m a x p softmax_p softmaxp 代表一个被用于所有可能 p=(a,b) 位置的softmax 函数, 在这种情况下,它也是整个2D格子。
这个机制基于仿射 x o T W Q T W K x p x_{o}^{T} W_{Q}^{T} W_{K} x_{p} xoTWQTWKxp汇集了全局的值 v p v_{p} vp 允许我们在整个特征地图中捕获相关但非本地的上下文,而不是仅能捕获局部关系的卷积。
然而,当输入的空间维度很大时,自我注意的计算成本非常高( O ( h 2 w 2 ) O(h^2w^2) O(h2w2)),它一般被限制使用在高层级的CNN中(即,下采样特征图)或小图像。另一个缺点是,全局池化不利用位置信息,而位置信息对于捕捉视觉任务中的空间结构或形状至关重要。
这两个问题可以通过在自注意力中添加局部约束和位置编码进行缓解,对于每个位置o,提取局部 m × m m×m m×m 个正方形区域以用作计算输出 y o y_o yo 的存储体。这显著地将其计算量减少到 O ( h w m 2 ) O(hwm^2) O(hwm2),允许自注意模块被部署为独立的层以形成完全自注意的神经网络。此外,一个学习到的相对位置编码项被纳入密切关系,产生在感受野中观察位置的动态先验(例如:局部的mxm 方形区域),形式化的表示为: y o = ∑ p ∈ N m × m ( o ) Softmax p ( q o T k p + q o T r p − o ) v p (2) y_{o}=\sum_{p \in \mathcal{N}_{m \times m}(o)} \operatorname{Softmax}_{p}\left(q_{o}^{T} k_{p}+q_{o}^{T} r_{p-o}\right) v_{p}\tag{2} yo=p∈Nm×m(o)∑Softmaxp(qoTkp+qoTrp−o)vp(2)可学习的向量 r p − o ∈ R d q r_{p-o} \in \mathbb{R}^{d_{q}} rp−o∈Rdq 是添加的相对位置编码,内积 q o T r p − o q_{o}^{T} r_{p-o} qoTrp−o 衡量位置 p = ( a , b ) p=(a,b) p=(a,b)到位置 o = ( i , j ) o=(i, j) o=(i,j)的相似性。
在实践中, d q d_{q} dq和 d out d_{\text {out}} dout比 d i n d_{in} din小得多, 并且可以在公式 (2)中扩展单头注意力到多头注意力,以此来捕获亲和力的混合。特别地,通过在 x o x_o xo 上并行应用N个单头注意来计算多头注意力,然后通过拼接每个头的结果,得到最终的输出 z o z_o zo,即 z o = c o n c a t n ( y o n ) z_o= concat_n\left(y_{o}^{n}\right) zo=concatn(yon).
Position-Sensitivity
我们注意到先前的位置偏置仅仅依赖于 x o x_{o} xo, 而不是 x p x_{p} xp, 然而 x p x_{p} xp 也可能具有关于要关注哪个位置的信息。除了查询相关偏置 q o T r p − o q q_{o}^{T} r_{p-o}^{q} qoTrp−oq,我们也添加了key相关位置偏置项 k p T r p − o k k_{p}^{T} r_{p-o}^{k} kpTrp−ok.
同理,公式2中的值 v p v_{p} vp 不包含任何位置信息,在大的感受野或记忆库的情况下, y o y_{o} yo 不太可能包含来自 v p v_{p} vp 的精确位置。因此,以前的模型必须在使用较小的感受野(i.e. m × m m \times m m×m 小区域)和抛弃精确的空间结构之间进行权衡。在本文中, 我们启用输出 y o y_{o} yo 来检索相对位置 r p − o v r_{p-o}^{v} rp−ov, 除了 v p v_{p} vp ,基于 q o T k p q_{o}^{T} k_{p} qoTkp ,表达式如下: y o = ∑ p ∈ N m × m ( o ) softmax p ( q o T k p + q o T r p − o q + k p T r p − o k ) ( v p + r p − o v ) (3) y_{o}=\sum_{p \in \mathcal{N}_{m \times m}(o)} \operatorname{softmax}_{p}\left(q_{o}^{T} k_{p}+q_{o}^{T} r_{p-o}^{q}+k_{p}^{T} r_{p-o}^{k}\right)\left(v_{p}+r_{p-o}^{v}\right)\tag{3} yo=p∈Nm×m(o)∑softmaxp(qoTkp+qoTrp−oq+kpTrp−ok)(vp+rp−ov)(3)
我们将这种设计称为位置敏感的自我注意,它以合理的计算开销捕获具有精确位置信息的远程交互,正如我们的实验所验证的那样。
Axial-Attention
由独立的自注意力模型提出的局部约束,在视觉任务中明显的减少了计算成本,能够建立完全自注意力模型,然而,这种约束牺牲了全局连接,使得注意力的感受野不大于具有相同内核大小的深度卷积。
此外,在局部正方形区域中执行的局部自注意力仍然具有与区域长度成二次方的复杂度,引入了另一个超参数来权衡性能和计算复杂度。
在这项工作中,我们建议在独立的自注意中采用轴向注意,以确保全局连接和高效计算。具体地说,我们首先将图像宽轴上的轴向注意层简单地描述为一维位置敏感的自注意,并对高度轴使用类似的定义。具体来说,沿宽度轴的轴向注意力层定义如下: y o = ∑ p ∈ N 1 × m ( o ) softmax p ( q o T k p + q o T r p − o q + k p T r p − o k ) ( v p + r p − o v ) (4) y_{o}=\sum_{p \in \mathcal{N}_{1 \times m}(o)} \operatorname{softmax}_{p}\left(q_{o}^{T} k_{p}+q_{o}^{T} r_{p-o}^{q}+k_{p}^{T} r_{p-o}^{k}\right)\left(v_{p}+r_{p-o}^{v}\right)\tag{4} yo=p∈N1×m(o)∑softmaxp(qoTkp+qoTrp−oq+kpTrp−ok)(vp+rp−ov)(4)一个轴向注意力层沿着一个特定的轴传播信息。为了捕获全局信息,我们分别为高度轴和宽度轴连续使用两个轴向注意力层。如上所述,两个轴向注意力层都采用了多头注意力机制。
Axial-attention 将复杂度降低到 O(hwm)。这启用了全局感受野,这是通过将跨度 m 直接设置为整个输入特征来实现的。或者也可以使用固定的 m 值,以减少巨大特征图上的内存占用。
Axial-ResNet
为了将 ResNet 转换为 Axial-ResNet,我们将残差瓶颈块中的 3x3 卷积替换为两个多头轴向注意层(一个用于高度轴,另一个用于宽度轴)。
在相应的轴向注意力层之后,在每个轴上执行可选的跨步。保留两个 1x1 卷积以调整特征。这形成了我们的(残差)轴向注意力块,如图2所示。将其堆叠多次以获得 Axial-ResNets

请注意,我们没有在两个轴向注意力层之间使用 1x1 卷积,因为矩阵乘法 ( W Q , W K , W V W_Q,W_K,W_V WQ,WK,WV) 紧随其后。此外,保留原始 ResNet 中的stem层(即第一个跨步7x7 卷积和 3x 3 最大池),产生一个 conv-stem 模型,其中第一层使用卷积,其他任何地方都使用注意力层。在 conv-stem 模型中,我们将跨度 m 设置为来自第一个块的整个输入,其中特征图为 56x56。
在我们的实验中,我们还构建了一个全轴向注意力模型,称为 Full Axial-ResNet,它进一步将轴向注意力应用于stem层。
而不是设计一个特殊的空间变化注意力stem层,而是简单地堆叠三个轴向注意力瓶颈块。此外,我们在 Full Axial-ResNets 的前几个块中采用局部约束(即 mxm 正方形区域),以降低计算成本。
Axial-DeepLab:
为了进一步将 Axial-ResNet 转换为 Axial-DeepLab 以进行分割任务,我们进行了一些更改,如下所述。
- 首先,为了提取密集的特征图,DeepLab改变了 ResNet 中最后一两个阶段的步幅和空洞率。同样,我们删除了最后阶段的步幅,但我们没有实现“atrous”注意力模块,因为我们的轴向注意力已经捕获了整个输入的全局信息。在这项工作中,我们提取输出步幅16(即输入分辨率与最终骨干特征分辨率的比率) 的特征图。我们不追求输出步幅 8,因为它的计算量很大。
- 其次,我们不采用空洞空间金字塔池化模块(ASPP),因为我们的轴向注意块也可以有效地编码多尺度或全局信息。我们在实验中表明,我们的没有 ASPP 的 Axial-DeepLab 在有和没有 ASPP 的情况下都优于 Panoptic-DeepLab 。
- 最后,在 Panoptic-DeepLab 之后,我们采用了完全相同的三个卷积、双解码器和预测头的茎tem。头部产生语义分割和与类无关的实例分割,并通过多数投票将它们合并以形成最终的全景分割。
- 在输入非常大(例如,2177x2177)并且内存受限的情况下,我们在所有轴向注意力块中采用大跨度 m = 65。请注意,我们不将轴向跨度视为超参数,因为它已经足以覆盖多个数据集上的远程甚至全局上下文,并且设置较小的跨度并不会显着减少 M-Adds.