【音效处理】Compressor 压缩器算法简介
系列文章目录
- Delay Line 简介及其 C/C++ 实现
- LFO 低频振荡器简介及其 C/C++ 实现
- 【音效处理】Delay/Echo 算法简介
- 【音效处理】Vibrato 算法简介
- 【音效处理】Reverb 混响算法简介
文章目录
- 系列文章目录
- 一、Compressor
-
- 1.1 动态范围
- 二、Compressor 算法实现
-
- 2.1 算法参数
- 2.1 算法建模
- 2.2 Gain Computer
- 2.3 Level detection
-
- 2.3.1 Peak detector
- 2.3.2 Level Corrected Peak Detectors
- 2.3.3 Smooth Peak Detectors
- 2.4 Feedforward or Feedback
- 2.5 Detector 放置的位置
- 总结
- 参考
一、Compressor
1.1 动态范围
Compressor 中文译为 “压缩器” 或者 “动态压缩器”,它是一种音频动态范围处理算法。所谓动态范围,以我粗鄙的理解它描述了:音频最大声的那个点与最小声那个点之间的差异范围。
举个例子,很多古典音乐的动态范围大,整首曲子中声音小的地方非常小,可能需要你提起耳朵仔细听,但在声音大的地方也震耳欲聋,例如 命运交响曲,贝多芬月光奏鸣曲 等,作者通过不同的音量来表达不同的情感,我们在听此类音乐时也能感受到作者想要表达的情绪;但在 流行/Pop等流派的音乐,从头到尾就是动次打次的,突出一个 “燥”,音量也是从始至终拉满,这样的音乐动态范围就小得多。
下面两个图是命运交响曲 和 贾斯汀比伯-Stay 的波形图,你现在应该很容易就能区分出哪个是哪个。

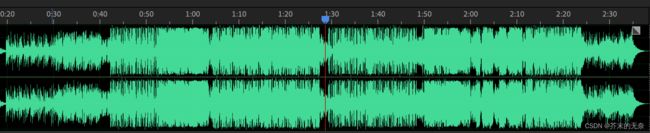
动态范围是大一点好,还是小一点好呢?这个问题始终存在争论,只能说仁者见仁,智者见智了。但非常明确的一点是,人们对于音频动态范围调整是有需求的。早期的广播仪器非常脆弱,过大的音量可能会导致保险丝过热烧毁,因此需要通过技术手段压缩音频的高潮部分;另外,人耳天生对响度大的音频更感兴趣,越来越多的歌手通过动态调整的技术来提升发行歌曲的响度,只要压缩高音量部分和提升低音量部分,牺牲动态范围来提升整体响度就可以了,这也是响度战争的由来。除开提升响度,似乎也有一些听上去很正当的理由,例如动态范围过大会容易导致人耳疲惫,通过动态压缩可以让歌曲听起来更轻松等等,这么说也不无道理,歌手可能认为”我的歌 happy 就完了,怎么 happy 怎么来“,动态范围啥的根本就不用管。
二、Compressor 算法实现
关于 Compressor 的具体算法,这里参考 Digital Dynamic Range Compressor Design— A Tutorial and Analysis,整篇论文对 Compressor 的算法描述十分详细,本人在这里只挑选重要部分进行说明,详细内容请大家自行参看论文。OK,让我们开始。
动态范围压缩算法(Dynamic Range Compression,DRC)是将音频信号的动态范围映射到一个较小的范围内的过程,即降低较高的峰值的信号电平,而不处理较安静的部分。DRC被广泛用于音频录制、制作工作、降噪、广播和现场表演等应用中。
与其他音效算法相比,Compressor 可能是最为复杂的一种,它的设计涉及多个方面,包括 Compressor 的拓扑结构、静态压缩特性、平滑滤波器的类型等等。对 Compressor 的设计进行分析是非常困难的,因为它是一个带状态的非线性时变系统。它以平滑的方式进行增益控制,而非静态的瞬时完成。此外,大量的设计选择让我们几乎不可能给出一个通用的 Compressor 设计框图。”没有两个 Compressor 的声音是一样的“ 有人这样评价到。
2.1 算法参数
Compressor 中常用的参数包括如下几种。
Threshold,定义了开始压缩的音量。任何超过阈值的信号都将被压缩。例如当 Threshold = -10db,当信号音量超过 -10db 时,它将被压缩。
Ratio,控制超过 Threshold 的信号的压缩比率。例如当 Threshold = -10,input = -5,此时信号超过 Threshold 有 5db,它将被压缩,那么压缩多少呢?这就由 Ratio 控制,当 Ratio = 5 时,信号增量从原来的 5db 被抑制为 1db,当 Ratio = 2 时,则抑制为 2.5db,以此类推。

Attack Time,Attack Time 和 Release Time 在一定程度上控制 Compressor ”灵敏度“。 Attack Time 定义了一旦信号超过 Threshold,Compressor 将增益降低到期望水平所需要的时间。
Release Time 定义了一旦信号低于 Threshold,将增益恢复至正常水平需要的时间。
Attack Time 和 Release Time 是 Compressor 中最不容易理解的两个参数,我们会在后面的 ”Level Detection“ 章节对这个两个参数有更深的理解,在这里我们简单地将它们理解为灵敏度即可。Attack Time 值越小,信号超过 Threshold 就会越快地被压缩,Release Time 越小,信号恢复的也越快。
你可能会有疑问,信号超过 Threshold,我们直接进行压缩即可,为啥需要 Attack Time 和 Release Time 呢?非也非也,如果如此简单粗暴的压缩方式会引入杂音,我们为了避免杂音,首先需要得到平滑的音量曲线,而”平滑“的特性就模糊了时间的精确度,因此引入 Attack Time 和 Release Time 满足人们对时间的某种控制。
Make-up Gain,Compressor 降低信号的增益,因此可以施加一个额外的增益使得输入信号与输出信号的响度水平相当。
Knee Width,它控制了压缩曲线的特性(如下图),曲线是尖锐的拐角,还是想膝盖一样有弧度的曲线。
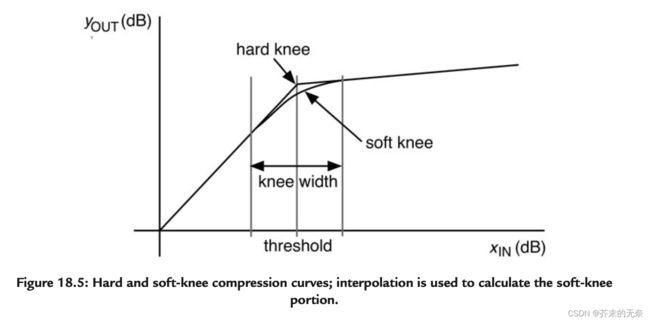
2.1 算法建模
进入 Compressor 的信号被分为两路,一路信号被送入侧链用于计算增益控制,另一路信号送入增益放大器中用于生成算法输出,总体结构如下图:

在数字信号设计中,如果 x [ n ] x[n] x[n] 表示输入信号, y [ n ] y[n] y[n]表示输出信号, c [ n ] c[n] c[n] 表示增益控制,那么 y [ n ] = c [ n ] ⋅ x [ n ] y[n] = c[n]\cdot x[n] y[n]=c[n]⋅x[n],此外还要加上 Make-up Gain 以弥补增益,当我们用分贝表示信号时, Compressor 算法模型为:
y d B [ n ] = x d B [ n ] + c d B [ n ] + M y_{d B}[n]=x_{d B}[n]+c_{d B}[n]+M ydB[n]=xdB[n]+cdB[n]+M
x d B [ n ] x_{d B}[n] xdB[n] 和 M M M 都容易得到,而如何得到 c d B [ n ] c_{d B}[n] cdB[n] 是 Compressor 算法的核心,概况来说想要得到 c d B [ n ] c_{d B}[n] cdB[n] 需要两个模块:Level Detection 和 Gain Computer
2.2 Gain Computer
Gain Computer 根据输入信号的电平(音量)来计算得到需要的增益。这个阶段涉及到了 Threshold(T)、Ratio(R)、Knee Width(W) 三个参数。一旦输入信号电平超过 T,那么它会根据 R 进行衰减,计算公式如下:
y G = { x G x G ≤ T T + ( x G − T ) / R x G > T y_{G}=\left\{\begin{array}{cc} x_{G} & x_{G} \leq T \\ T+\left(x_{G}-T\right) / R & x_{G}>T \end{array}\right. yG={xGT+(xG−T)/RxG≤TxG>T
其中 x G x_G xG 为输入信号电平, y G y_G yG 为输出电平。
为了让 Compressor 有更加平滑的变化曲线,我们增加了 Knee Width(参考 Knee Width 参数说明图),这中模式我们称为 “Soft Knee”,其计算公式为:
y G = { x G 2 ( x G − T ) < − W x G + ( 1 / R − 1 ) ( x G − T + W / 2 ) 2 / ( 2 W ) 2 ∣ ( x G − T ) ∣ ≤ W T + ( x G − T ) / R 2 ( x G − T ) > W y_{G}=\left\{\begin{array}{cc} x_{G} & 2\left(x_{G}-T\right)<-W \\ x_{G}+(1 / R-1)\left(x_{G}-T+W / 2\right)^{2} /(2 W) & 2\left|\left(x_{G}-T\right)\right| \leq W \\ T+\left(x_{G}-T\right) / R & 2\left(x_{G}-T\right)>W \end{array}\right. yG=⎩⎨⎧xGxG+(1/R−1)(xG−T+W/2)2/(2W)T+(xG−T)/R2(xG−T)<−W2∣(xG−T)∣≤W2(xG−T)>W
2.3 Level detection
Level detection 的作用是提供信号电平的平滑表示。Attack Time 和 Release Time 将在这个阶段起作用,这两个参数对于 Compressor 算法调参也是至关重要的,如果选择了不合适的参数,很有可能导致音频出现杂音。
Attack time 和 Release time 是通过一个平滑滤波器引入的。我们可以简单模拟这个滤波器的行为:
s [ n ] = α s [ n − 1 ] + ( 1 − α ) r [ n ] s[n]=\alpha s[n-1]+(1-\alpha) r[n] s[n]=αs[n−1]+(1−α)r[n]
α \alpha α 是滤波器系数, r [ n ] r[n] r[n] 是输入信号, s [ n ] s[n] s[n] 是输出信号。我们对这个滤波器输入阶跃信号,其输出为:
s [ n ] = 1 − α n for x [ n ] = 1 , n ≥ 1 s[n]=1-\alpha^{n} \quad \text { for } \quad x[n]=1, n \geq 1 s[n]=1−αn for x[n]=1,n≥1
我们假设过了时间 τ \tau τ 后,信号上升至 1 − 1 e 1-\frac{1}{e} 1−e1,也就是说 s [ τ f x s ] = 1 − 1 e s[\tau f_xs] = 1 - \frac{1}{e} s[τfxs]=1−e1,可以得到:
α = e − 1 / ( τ f s ) (1) \alpha=e^{-1 /\left(\tau f_{s}\right)} \tag{1} α=e−1/(τfs)(1)
了解了这个知识点后,我们就可以对 Attack time 和 Release time 有更深的理解了。当我们说 Attack time = 200ms 时,其实表达的是,对 level detection 这个系统输入阶跃信号,它的输出将在 200ms 上升至 1 − 1 e ≈ 0.632 1-\frac{1}{e} \approx 0.632 1−e1≈0.632;当我们说 Release time = 200ms 时,其实表达的是,停止阶跃信号的输入,转而输入 0 电平信号,它的输出衰减至 1 e ≈ 0.367 \frac{1}{e} \approx 0.367 e1≈0.367 需要 200ms。
如上所述,你应该大致可以理解为什么我之前说可以将 attack time 和 release time 理解成 “灵敏度” 了。attack time 越小,输出信号上升越快,越快接近输入信号电平,release time 同理。
当信号电平由其绝对值决定时,这被称为 peak 模式。另一种使用的是电平的均方根,这被称为是 RMS 模式。
RMS 模式不是我们讨论的重点,在一个实时系统中,RMS 模式的实现为:
y L 2 [ n ] = α y L 2 [ n − 1 ] + ( 1 − α ) x L 2 [ n ] y_{L}^{2}[n]=\alpha y_{L}^{2}[n-1]+(1-\alpha) x_{L}^{2}[n] yL2[n]=αyL2[n−1]+(1−α)xL2[n]
大多数 Compressor 使用 peak 模式,接下来将重点讨论它。
2.3.1 Peak detector
第一种要介绍的 peak detector 是用模拟电路转换而来,它的差分方程为:
y L [ n ] = α R y L [ n − 1 ] + ( 1 − α A ) max ( x L [ n ] − y L [ n − 1 ] , 0 ) \begin{aligned} y_{L}[n]=& \alpha_{R} y_{L}[n-1] \\ &+\left(1-\alpha_{A}\right) \max \left(x_{L}[n]-y_{L}[n-1], 0\right) \end{aligned} yL[n]=αRyL[n−1]+(1−αA)max(xL[n]−yL[n−1],0)
其中 α R \alpha_{R} αR 和 α A \alpha_{A} αA 分别表示 Release time 和 Attack time 根据公式(1)得到的 α \alpha α 系数。
这种 peak detector 在很多 Compressor 中被使用,但它又明显的缺陷。
首先,如果 x L [ n ] ≥ y L [ n − 1 ] x_{L}[n] \geq y_{L}[n-1] xL[n]≥yL[n−1] 时,阶跃信号的冲激响应变成了:
y [ n ] = ( 1 − α A ) ∑ m = 0 n − 1 ( α R + α A − 1 ) m → 1 − α A 2 − α R − α A ≈ τ R τ R + τ A \begin{aligned} y[n]=&\left(1-\alpha_{A}\right) \sum_{m=0}^{n-1}\left(\alpha_{R}+\alpha_{A}-1\right)^{m} \\ & \rightarrow \frac{1-\alpha_{A}}{2-\alpha_{R}-\alpha_{A}} \approx \frac{\tau_{R}}{\tau_{R}+\tau_{A}} \end{aligned} y[n]=(1−αA)m=0∑n−1(αR+αA−1)m→2−αR−αA1−αA≈τR+τAτR
我们希望 y [ n ] y[n] y[n] 应该是无限接近 1 的,也就是说 τ R τ R + τ A ≈ 1 \frac{\tau_{R}}{\tau_{R}+\tau_{A}} \approx 1 τR+τAτR≈1,这只在 τ R ≫ τ A \tau_{R} \gg \tau_{A} τR≫τA 才满足。
此外, Attack time 也会被 Release time 略微放大:当我们使用快速的 release time 时,会出现更快的 attack time,下图说明了这种情况:

总而言之,因为 attack time 和 release time 相互影响,且在某些情况下信号失准,因此我们需要改进它。
2.3.2 Level Corrected Peak Detectors
作者提出了优化过的 decoupled peak detector 和 branching peak detector。
decoupled peak detector 公式为:
y 1 [ n ] = max ( x L [ n ] , α R y 1 [ n − 1 ] ) y L [ n ] = α A y L [ n − 1 ] + ( 1 − α A ) y 1 [ n ] \begin{array}{l} y_{1}[n]=\max \left(x_{L}[n], \alpha_{R} y_{1}[n-1]\right) \\ y_{L}[n]=\alpha_{A} y_{L}[n-1]+\left(1-\alpha_{A}\right) y_{1}[n] \end{array} y1[n]=max(xL[n],αRy1[n−1])yL[n]=αAyL[n−1]+(1−αA)y1[n]
branching peak detector 公式为:
y L [ n ] = { α A y L [ n − 1 ] + ( 1 − α A ) x L [ n ] x L [ n ] > y L [ n − 1 ] α R y L [ n − 1 ] x L [ n ] ≤ y L [ n − 1 ] y_{L}[n]=\left\{\begin{array}{ll} \alpha_{A} y_{L}[n-1]+\left(1-\alpha_{A}\right) x_{L}[n] & x_{L}[n]>y_{L}[n-1] \\ \alpha_{R} y_{L}[n-1] & x_{L}[n] \leq y_{L}[n-1] \end{array}\right. yL[n]={αAyL[n−1]+(1−αA)xL[n]αRyL[n−1]xL[n]>yL[n−1]xL[n]≤yL[n−1]
下图是 decoupled 和 branching detector 在相同 attack time 不同 release time 下的输出,可以看到 branching detector 预期的 release time 是非常准确的,而 decoupled detector 产生了大约为 τ R + τ A \tau_R + \tau_A τR+τA 的时间,并不是那么准确。
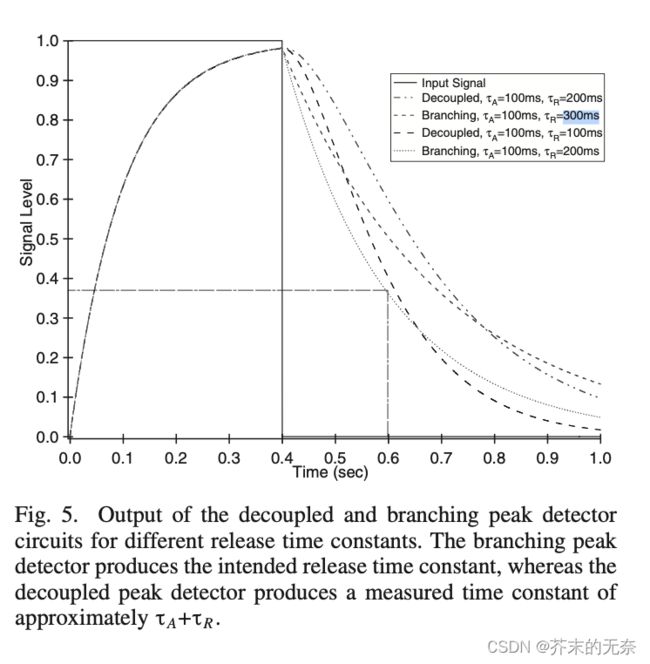
2.3.3 Smooth Peak Detectors
之前所有设计有个缺陷:只有输入达到峰值接着返回 0 后,才会利用所有的 release time。然而,但信号稳定在一个不是 0 的水平时,释放包络就会在这一点停止,release time 将会比我们预期的短得多(见下面的图例)。为了优化这一点,提出了 smooth decoupled peak detector 和 smooth branching peak detector。
smooth branching peak detector 差分方程为:
y L [ n ] = { α A y L [ n − 1 ] + ( 1 − α A ) x L [ n ] x L [ n ] > y L [ n − 1 ] α R y L [ n − 1 ] + ( 1 − α R ) x L [ n ] x L [ n ] ≤ y L [ n − 1 ] y_{L}[n]=\left\{\begin{array}{ll} \alpha_{A} y_{L}[n-1]+\left(1-\alpha_{A}\right) x_{L}[n] & x_{L}[n]>y_{L}[n-1] \\ \alpha_{R} y_{L}[n-1]+\left(1-\alpha_{R}\right) x_{L}[n] & x_{L}[n] \leq y_{L}[n-1] \end{array}\right. yL[n]={αAyL[n−1]+(1−αA)xL[n]αRyL[n−1]+(1−αR)xL[n]xL[n]>yL[n−1]xL[n]≤yL[n−1]
smooth decoupled peak detector 差分方程为:
y 1 [ n ] = max ( x L [ n ] , α R y 1 [ n − 1 ] + ( 1 − α R ) x L [ n ] ) y L [ n ] = α A y L [ n − 1 ] + ( 1 − α A ) y 1 [ n ] \begin{array}{l} y_{1}[n]=\max \left(x_{L}[n], \alpha_{R} y_{1}[n-1]+\left(1-\alpha_{R}\right) x_{L}[n]\right) \\ y_{L}[n]=\alpha_{A} y_{L}[n-1]+\left(1-\alpha_{A}\right) y_{1}[n] \end{array} y1[n]=max(xL[n],αRy1[n−1]+(1−αR)xL[n])yL[n]=αAyL[n−1]+(1−αA)y1[n]
下图为以上 4 种 peak detector 实际信号输出
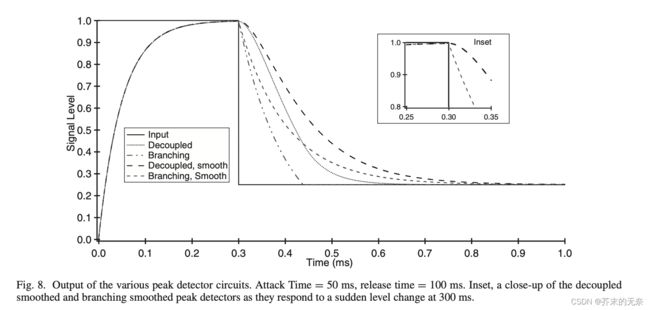
那么有这种多中 peak detector 我们应该选择哪一个呢?论文对这几种 peak detector 做了实验评测,并给出结论:
- 如果我们希望得到更平稳、更连续、对音色修改最小的信号,应该使用 smooth decoupled peak detector
- 如果我们想要对时间系数有更精确的控制,那么可以使用 smooth branching peak detector,但它可能会在 release 和 attack 阶段切换之间产生不连续的信号。
最后,贴上 peak detectors 的 python 实现代码链接:jiemojiemo - peak_detectors.ipynb
2.4 Feedforward or Feedback
现在我们已经搞定了 peak detector 和 gain computer 两个模块了,现在思考下一个问题:side-chain 中的拓扑设计,我们应该使用 feedforward 还是 feedback ?
下图中,最上面的是 feedforwad 结构,下面两种是 feedback 结构。
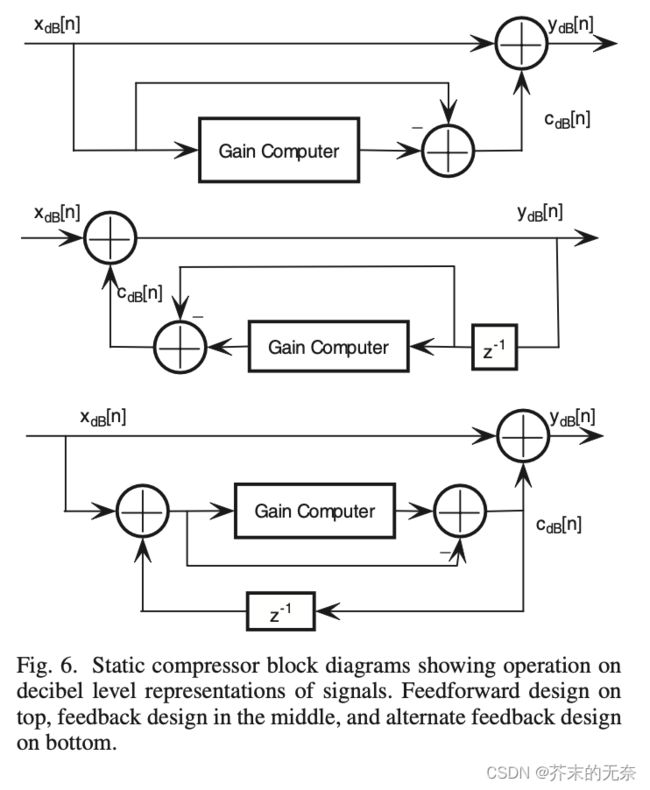
关于这部分内容,我没有细看,直接抄作者结论:应该使用 feedforward 结构,因为它们比 feedback 更加稳定,而且不会出现高动态范围的问题。
2.5 Detector 放置的位置
Detector 在 side-chain 中放置的位置有很多种,如下图

对于 a 结构,先做 peak detection,后接 gain computer :
x L [ n ] = ∣ x [ n ] ∣ x G [ n ] = 20 log 10 y L [ n ] c d B [ n ] = y G [ n ] − x G [ n ] \begin{aligned} x_{L}[n] &=|x[n]| \\ x_{G}[n] &=20 \log _{10} y_{L}[n] \\ c_{d B}[n] &=y_{G}[n]-x_{G}[n] \end{aligned} xL[n]xG[n]cdB[n]=∣x[n]∣=20log10yL[n]=yG[n]−xG[n]
这种结构有个问题:它不够平滑。peak detection 的结果只有在超过 Threshold 时,gain computer 才开始工作,这种不连续性会可能会导致杂音。
此外,peak detection 还会引入延迟,gain computer 计算出的结果,实际上是前面信号的增益控制。
针对 a 结构,提出了 b 结构的优化。额…b 结构有点复杂,我没看懂,所以直接来到 c 结构,先做 gain computer 后接 level detection:
x G [ n ] = 20 log 10 ∣ x [ n ] ∣ x L [ n ] = 1 0 y G [ n ] / 20 c [ n ] = y L [ n ] \begin{aligned} x_{G}[n] &=20 \log _{10}|x[n]| \\ x_{L}[n] &=10^{y_{G}[n] / 20} \\ c[n] &=y_{L}[n] \end{aligned} xG[n]xL[n]c[n]=20log10∣x[n]∣=10yG[n]/20=yL[n]
c 结构的想法非常有趣,之前我老觉得 level detection 负责检测电平,然后再送给 gain computer 才是符合逻辑的,如此,level detection 输出时连续平滑的,但 gain computer 不是。而 c 结构,让 gain computer 和 level detection 都是平滑的了。妙啊。
总结
我们介绍了 Compressor 算法中的细节部分,包括 gain computer、level detection、side-chain 拓扑结构,detector 放置位置等。回顾全文可以看到,compressor 算法实现多种多种,不同结构之间有微妙的差别。论文作者推荐使用的配置是:
- 使用 feedforwad 拓扑结构
- 使用 smooth decoupled peak detector 后者 smooth branching peak detector
- 将 peak detector 放置在 gain computer 后面,采用 c 结构
最后展示下自己实现的 Compressor :
compressor_video
参考
- 音频动态处理原理和使用
- What is Dynamic Processing
- 「响度战争」是什么?它对唱片业产生了怎样的影响? - 丧心病狂刘老湿的回答 - 知乎
- jiemojiemo - peak_detectors.ipynb