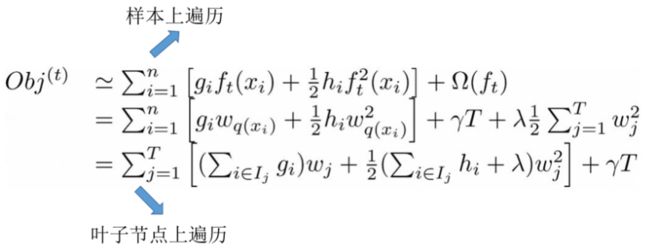【机器学习算法实践】xgboost，一种boosting工程思想，泰勒的二阶展开近似拟合数据分布，建议细看原论文

• XGBoost（eXtreme Gradient Boosting）极致梯度提升，是一种基于GBDT【机器学习算法实践】GBDT提升树，集成学习boosting方法，可分类课可回归，CART树是基础，调参是重点_羞儿的博客-CSDN博客的算法或者说工程实现。XGBoost的基本思想和GBDT相同，但是做了一些优化，比如二阶导数使损失函数更精准；正则项避免树过拟合；Block存储可以并行计算等。XGBoost具有高效、灵活和轻便的特点，在数据挖掘、推荐系统等领域得到广泛的应用。XGBoost 主要是用来解决有监督学习问题，此类问题利用包含多个特征的训练数据 $x_i$ ，来预测目标变量 $y_i$ 。

• 2016年，陈天奇在论文《 XGBoost：A Scalable Tree Boosting System》[1603.02754] XGBoost: A Scalable Tree Boosting System (arxiv.org)中正式提出。作为一种前向加法模型，他的核心是采用集成思想——Boosting思想，将多个弱学习器通过一定的方法整合为一个强学习器。即用多棵树共同决策，并且用每棵树的结果都是目标值与之前所有树的预测结果之差 并将所有的结果累加即得到最终的结果，以此达到整个模型效果的提升。XGBoost是由多棵CART(Classification And Regression Tree)，即分类回归树组成，因此他可以处理分类回归等问题。

• XGBoost是2016年由华盛顿大学陈天奇老师带领开发的一个可扩展机器学习系统。严格意义上讲XGBoost并不是一种模型，而是一个可供用户轻松解决分类、回归或排序问题的软件包。它内部实现了梯度提升树(GBDT)模型，并对模型中的算法进行了诸多优化，在取得高精度的同时又保持了极快的速度，在一段时间内成为了国内外数据挖掘、机器学习领域中的大规模杀伤性武器。

• XGBoost采用迭代预测误差的方法串联。举个通俗的例子，我们现在需要预测一辆车价值3000元。我们构建决策树1训练后预测为2600元，我们发现有400元的误差，那么决策树2的训练目标为400元，但决策树2的预测结果为350元，还存在50元的误差就交给第三棵树……以此类推，每一颗树用来估计之前所有树的误差，最后所有树预测结果的求和就是最终预测结果！

• XGBoost是基于CART树的集成模型，它的思想是串联多个决策树模型共同进行决策。XGBoost底层实现了GBDT算法，并对GBDT算法做了一系列优化：

  • 1. 对目标函数进行了泰勒展示的二阶展开，可以更加高效拟合误差。
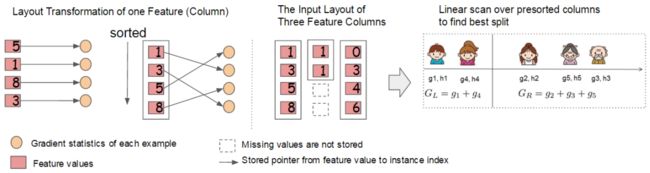
    2. 提出了一种估计分裂点的算法加速CART树的构建过程，同时可以处理稀疏数据。
    3. 提出了一种树的并行策略加速迭代。
    4. 为模型的分布式算法进行了底层优化。

• 算法推导

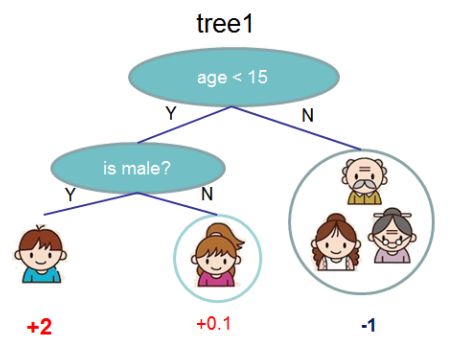
  • 我们把家庭中的成员分到了不同的叶子节点，同时每个叶子节点上都有一个分数。CART与决策树相比，细微差别在于CART的叶子节点仅包含判断分数。在CART中，相比较于分类结果，每个叶子节点的分数给我们以更多的解释。

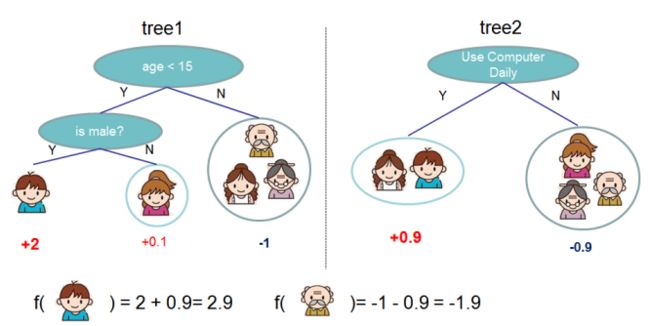
  • 下图是一个预测一家人喜欢电脑游戏的回归问题。可以看到样本落到叶子结点，对应的权重即为样本的回归分数。多棵树的预测结果即为最终的结果。

  • 

  • 上面的模型可定义为：$\widehat{y_i}={\sum }_{k=1}^K{f}_k(x_i),f_k\in \mathcal{F}$，其中，K表示树的数目，f表示函数空间F中的一个函数，代表树这种抽象结构。那么$y_i\prime$ 表示的即为最终预测结果。我们定义目标函数为：$obj(\theta )={\sum }_i^{n}l(y_i,\widehat{y_i})+{\sum }_{k=1}^K\Omega (f_k)$。

  • 目标函数：训练误差 + 正则化，根据对 $y_i$ 的不同理解，我们可以把问题分为，回归、分类、排序等。我们需要针对训练数据，尝试找到最好的参数。为此，我们需要定义所谓的目标函数，此函数用来度量参数的效果。

  • 其中，$l$ 为我们的损失函数，Ω为惩罚项。它在形式上如下图所示：$\Omega (f_t)=\gamma T+\frac{1}{2}\lambda {\sum }_{j=1}^T{w}_j^2$。

    • 

    • $\Omega =\gamma 3+\frac{1}{2}(2^2+0.1^2+(-1{)}^2)$。

  • 对于增量模型的定义，我们是用每一个树的预测结果去拟合上一棵树预测结果的残差，这样整体的树模型效果才会越来越好。

    • $$\begin{array}{rl}{\widehat{y_i}}^{(0)}& =0\\ {\widehat{y_i}}^{(1)}& =f_0(x_i)+f_1(x_i)={\widehat{y_i}}^{(0)}+f_1(x_i)\\ {\widehat{y_i}}^{(2)}& =f_0(x_i)+f_1(x_i)+f_2(x_i)={\widehat{y_i}}^{(1)}+f_2(x_i)\\ & ...\\ {\widehat{y_i}}^{(t)}& =\sum _{k=1}^K={\widehat{y_i}}^{(t-1)}+f_t(x_i)\end{array}$$

    • 可以看到，0棵树模型的预测结果为0，一颗树模型的预测结果为第一颗树的表现，在数值上等于上一课的预测结果加上当前树的表现；2棵树模型的预测结果等于第一颗树的表现加上第2棵树的表现，在数值上也等于上一课的预测结果加上当前树的表现；因此，我们可以得到t棵树模型的预测结果，在数值上等于前面t-1棵树的预测结果，加上第t棵树的表现。那么对于t棵树我们的目标函数为：

    • $$\begin{array}{rl}& 目标：Obj(t)=\sum _{n=1}^{n}l(y_i,{\widehat{y_i}}^{(t-1)}+f_t(x_i))+\Omega (f_t)+constant\\ & 使用泰勒展开式近似我们的目标：\\ & 泰勒展开式：f(x+\Delta (x))\approx f(x)+f^{\prime }(x)\Delta x+\frac{1}{2}{f}^{\prime \prime }(x)\Delta x^2\\ & 假设：g_i={\delta }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)}),h_i={\delta }_{{\hat{y}}^{(t-1)}}^{2}l(y_i,{\hat{y}}^{(t-1)})\\ & 则有：Obj(t)\approx \sum _{n=1}^n[l(y_i,{\widehat{y_i}}^{(t-1)}+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i))]+\Omega (f_t)+constant\end{array}$$

    • 因为，当我们求到 t 棵树模型时，前面t-1树的结果或是结构肯定是已经是确定了的，所以我们将它视为常数便得到上图的最后一个式子。这里的$g_i$和$h_i$是我们的损失函数关于${\widehat{y_i}}^{(t-1)}$ 的一阶、二阶导数，只要损失函数确定，我们的$g_i，h_i$就确定了。比如，当我们选取MSE，即均方误差作为损失：

    • $$\begin{gathered} g_i={\delta }_{{\hat{y}}^{(t-1)}}({\hat{y}}^{(t-1)}-y_i{)}^2=2({\hat{y}}^{(t-1)}-y_i), \\ {h}_i={\delta }_{{\hat{y}}^{(t-1)}}^2({\hat{y}}^{(t-1)}-y_i)=2 \end{gathered}$$

    • 可以看到，这里的梯度值其实就是前面t-1棵树与当前树模型的差值，我们称之为残差。每次我们加的梯度，就是用残差去拟合上几棵树预测的结果，只有这样我们的模型才可能更精确，更接近我们的真实值。

  • 接着，我们对上面的目标函数进行处理：

    • 

    • 这里我们定义上面的f(x): $f_t(x)=w_q(x),w\in R^T,q:R^d\to \{1,2,...,T\}$。其中w表示叶子结点上的分数所组成的向量，即我们的权重向量；q表示一种映射关系，即每个数据样本对应的叶子结点。那么一棵树的结构就可以描述为叶子结点对应权重的组合。同时，我们定义 $I_j=\left\{i\mid q\left(x_i\right)=j\right\}$,表示某个样本映射到的结点集合。因为多个样本会落到一个结点，所以这里的n>T。同时，我们也将目标函数的定义范围由n个样本转变为了T个结点。因为映射到同一叶子结点上的样本的权重都相同，所以我们继续对上图中的式子进行处理：

    • $$\begin{gathered} G_j=\sum _{i\in I_j}{g}_i,H_j=\sum _{i\in I_j}{h}_i \\ Obj(t)=\sum _{j=1}^T[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2]+\gamma T \end{gathered}$$

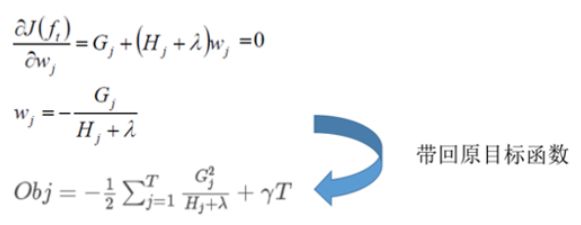
    • 因为 $G_j,H_j$ 都是前t-1棵树已经确定了的，因此对于一棵确定的树，即T已知的情况下，此时我们的目标函数就只和 $w_j$ 相关了，易知：对 $w_j$ 求偏导，偏导数为0时的w值，代入目标函数将取得最小值。(隐含条件是 $H_j$ 必须为正值)如下图所示：

    • 

    • 再回到上面，对于一个确定的树结构q(x)，我们便能求得目标函数，有了目标函数，我们树模型的评判标准便也就确定了。见下图：

    • 

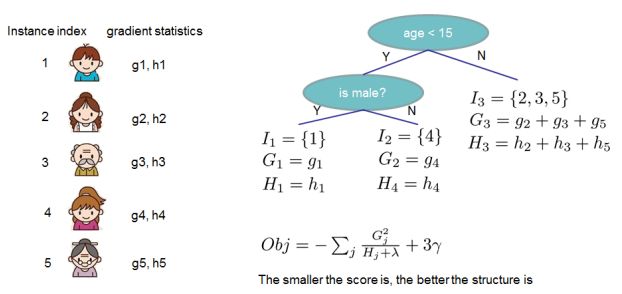
    • 那么，如何确定树的结构呢？这就涉及到分裂点选择的问题了。最原始的猜想就是枚举出所有可能的树结构，即特征值和分裂阀值，然后再根据目标函数计算比较出最优的选择。比如，当我们的结点按如下方式进行划分：（这里做了一个简单的年龄排序）

    • 

    • 现在我们已经知道一旦树的结构固定下来以后，如何来计算叶子节点上的分数，以及计算这棵树的优劣。那么关于现在我们要来解决如何来学习这棵树的结构。比较简单粗暴的方法就是遍历所有可能的树结构，然后从中找到最好的那棵树。但是这也是不切实际的，因为需要遍历的情况实在是太多了。所以我们来寻求一种贪婪的解法，就是在树的每个层构建的过程中，来优化目标。那么这里假设在某一层的构建过程中，假设特征已经选定，我们先如何进行二叉划分呢，以及是不是需要进行划分？我们可以通过下面的式子来计算划分之后，在目标上所获得的收益（这个收益越越好，负数表示收益为负）,那么使用我们的目标函数对这次划分做出评判，即切分前的obj减去切分后的obj：

    • $$Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_L{)}^2}{H_L+H_R+\lambda }]-\gamma$$

    • 如果增益Gain为正值，说明切分后的obj更小，模型更好。类似的，其他结点也递归的重复这个过程，直到达到树的最大深度，或是当样本权重和小于设定阈值时停止生长以防止过拟合。这样一颗树的训练过程就完成了。下一棵树的训练过程同样是计算梯度，然后确定树结构。

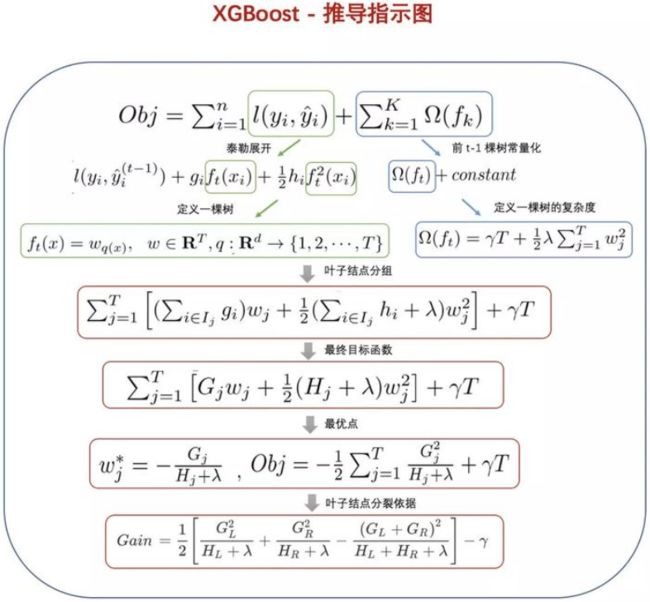
  • 至此，我们的XGBoost算法的树模型训练过程就结束了，这里引用一张图，梳理一下推导过程。

    • 

• 生成树过程

  • 很有意思的一个事是，我们从头到尾了解了xgboost如何优化、如何计算，但树到底长啥样，我们却一直没看到。很显然，一棵树的生成是由一个节点一分为二，然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂，XGBoost作者在其原始论文中给出了一种分裂节点的方法：枚举所有不同树结构的贪心法。

  • 不断地枚举不同树的结构，然后利用打分函数来寻找出一个最优结构的树，接着加入到模型中，不断重复这样的操作。这个寻找的过程使用的就是贪心算法。选择一个feature分裂，计算loss function最小值，然后再选一个feature分裂，又得到一个loss function最小值，你枚举完，找一个效果最好的，把树给分裂，就得到了小树苗。

  • 总而言之，XGBoost使用了和CART回归树一样的想法，利用贪婪算法，遍历所有特征的所有特征划分点，不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益，同时为了限制树生长过深，还加了个阈值，只有当增益大于该阈值才进行分裂。从而继续分裂，形成一棵树，再形成一棵树，每次在上一次的预测基础上取最优进一步分裂/建树。

• 如何停止树的循环生成

  • 当引入的分裂带来的增益小于设定阀值的时候，我们可以忽略掉这个分裂，所以并不是每一次分裂loss function整体都会增加的，有点预剪枝的意思，阈值参数为（即正则项里叶子节点数T的系数）；

  • 当树达到最大深度时则停止建立决策树，设置一个超参数max_depth，避免树太深导致学习局部样本，从而过拟合；

  • 样本权重和小于设定阈值时则停止建树。什么意思呢，即涉及到一个超参数-最小的样本权重和min_child_weight，和GBM的 min_child_leaf 参数类似，但不完全一样。大意就是一个叶子节点样本太少了，也终止同样是防止过拟合；

• XGBoost与GBDT有什么不同

  • GBDT是机器学习算法，XGBoost是该算法的工程实现。

  • 在使用CART作为基分类器时，XGBoost显式地加入了正则项来控制模 型的复杂度，有利于防止过拟合，从而提高模型的泛化能力。

  • GBDT在模型训练时只使用了代价函数的一阶导数信息，XGBoost对代价函数进行二阶泰勒展开，可以同时使用一阶和二阶导数。

  • 传统的GBDT采用CART作为基分类器，XGBoost支持多种类型的基分类器，比如线性分类器。

  • 传统的GBDT在每轮迭代时使用全部的数据，XGBoost则采用了与随机森林相似的策略，支持对数据进行采样。

  • 传统的GBDT没有设计对缺失值进行处理，XGBoost能够自动学习出缺失值的处理策略。

• XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。

训练XGBoost简单demo

• 导包加载数据

  • %pip install xgboost
    # 数据是libsvm格式，很适合用于**稀疏存储**的数据：
    # 例如 0 1:1 9:1 19:1 21:1 24:1 ...
    # 第1列是target 后面是index:数值
    import numpy as np  # 数值计算，处理
    import scipy.sparse
    # 由于稀疏矩阵中非零元素较少，零元素较多，因此可以采用只存储非零元素的方法来进行压缩存储。
    # 对于一个用二维数组存储的稀疏矩阵Amn，如果假设存储每个数组元素需要L个字节，那么存储整个矩阵需要m*n*L个字节。
    # 但是，这些存储空间的大部分存放的是0元素，从而造成大量的空间浪费。为了节省存储空间，可以只存储其中的非0元素。大大减少了空间的存储。
    # python不能自动创建稀疏矩阵，所以要用scipy中特殊的命令来得到稀疏矩阵。
    import pickle # python2中叫cPickle python3中改为pickle
    import xgboost as xgb
    data_dir = './data/'
    # 读取数据集
    # xgb.DMatrix()可以直接读取libsvm格式的数据
    dtrain = xgb.DMatrix(data_dir + 'agaricus.txt.train')
    dtest = xgb.DMatrix(data_dir + 'agaricus.txt.test')
    print(dtrain)
    

  • <xgboost.core.DMatrix object at 0x00000151E2B9C7F0>
    

• 设定模型参数

  • param = {'max_depth':2,  # 树深
             'eta': 1,
             'verbosity': 0,
             'objective': 'binary:logistic'}
    watch_list = [(dtest, 'eval'), (dtrain, 'train')]
    number_round = 10 # 跑10轮（10棵子树） # 通用参数
    # 训练
    model = xgb.train(param, dtrain, num_boost_round=number_round, evals=watch_list)  
    # 预测
    pred = model.predict(dtest) # 返回的是numpy.array
    print(type(pred), pred.dtype, pred.shape) # (1611,)
    # groundtruth
    labels = dtest.get_label()
    print(type(labels), labels.dtype, labels.shape)
    print(labels[:10])
    error_num = sum([i for i in range(len(pred)) if int(pred[i]>0.5)!=labels[i]])
    print(error_num)
    

  • [0]    eval-logloss:0.22669    train-logloss:0.23338
    [1]    eval-logloss:0.13787    train-logloss:0.13666
    [2]    eval-logloss:0.08046    train-logloss:0.08253
    [3]    eval-logloss:0.05833    train-logloss:0.05647
    [4]    eval-logloss:0.03829    train-logloss:0.04151
    [5]    eval-logloss:0.02663    train-logloss:0.02961
    [6]    eval-logloss:0.01388    train-logloss:0.01919
    [7]    eval-logloss:0.01020    train-logloss:0.01332
    [8]    eval-logloss:0.00848    train-logloss:0.01113
    [9]    eval-logloss:0.00692    train-logloss:0.00663   
    <class 'numpy.ndarray'> float32 (1611,)
    <class 'numpy.ndarray'> float32 (1611,)
    [0. 1. 0. 0. 0. 0. 1. 0. 1. 0.]
    0
    

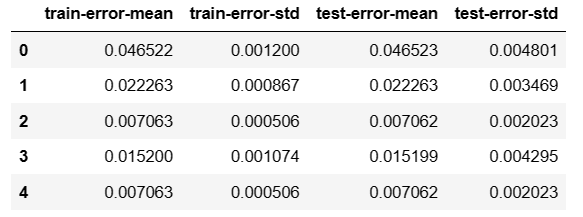
• 交叉验证

  • number_round = 5 # 通用参数
    # nfold=5折
    xgb.cv(param, dtrain, number_round, nfold=5, metrics={'error'}, seed=3)
    

  • 

• 调整样本权重

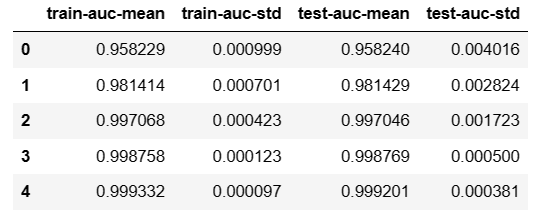
  • # 看一下正负例的比例，然后调整一下权重
    def preproc(dtrain, dtest, param):
        labels = dtrain.get_label()
        ratio = float(np.sum(labels==0))/np.sum(labels==1)
        param['scale_pos_ratio'] = ratio
        return (dtrain, dtest, param)
    xgb.cv(param, dtrain, number_round, nfold=5, metrics={'auc'}, seed=3, fpreproc=preproc)
    # auc值越接近1效果越好
    

  • 

• 自定义目标函数（损失函数）

  • 目标函数：预测与label的接近程度，值越大越好，梯度上升

  • 损失函数：预测与label的差距程度，值越小越好，梯度下降

  • xgboost中如果要使用自定义目标函数，就要自己提供一阶导数和二阶导数的实现

  • # 自定义目标函数：log似然，交叉验证
    # 需要提供一阶导数和二阶导数
    def logregobj(pred, dtrain):
        labels = dtrain.get_label()
        pred = 1. / (1+np.exp(-pred)) # sigmoid
        grad = pred - labels # 1阶导数
        hess = pred*(1-pred) # 2阶导数（海森矩阵），sigmoid的导数：g'(x)=g(x)(1-g(x))
        return grad, hess
    """
    在逻辑回归章节，求导时，梯度=X.T.dot(h_x-y)，为什么上面只写了(h_x-y)
    这里的p-y.label，其实只是梯度的“公共部分”，因为不同的样本要乘以各自的样本值，
    所以是无法提前算出来的，因此往往用p-y.label计算梯度的系数部分，实际拿到样本，再乘以各自的数据。
    """
    def evalerror(pred, dtrain):
        labels = dtrain.get_label()
        error_num = float(sum(labels!=(pred>0.))) # sigmoid函数g(z)>0.5的话，要z>0.
        return 'error', error_num/len(labels)
    # 模型参数
    param = {'max_depth':2,  # 树深
             'eta': 1,
             'verbosity': 0,}
    watch_list = [(dtest, 'eval'), (dtrain, 'train')]
    number_round = 10 # 通用参数
    # 自定义目标函数训练
    model = xgb.train(param, dtrain,
                      num_boost_round=number_round,
                      evals=watch_list,
                      obj=logregobj, # 目标函数
                      custom_metric=evalerror) # 评价函数
    xgb.cv(param, dtrain, number_round, nfold=5, seed=3, obj=logregobj, feval=evalerror)
    

  • 

• 用前n棵树做预测,number_round = 10 做了10轮，就会有10棵树产生,但是可以仅使用前几棵树做预测

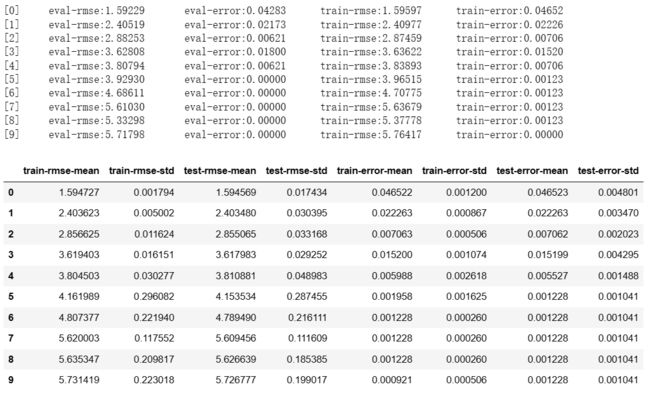
  • pred1 = model.predict(dtest, ntree_limit=1)
    print(evalerror(pred1, dtest))
    pred2 = model.predict(dtest, ntree_limit=2)
    print(evalerror(pred2, dtest))
    pred3 = model.predict(dtest, ntree_limit=3)
    print(evalerror(pred3, dtest))
    

  • ('error', 0.04283054003724395)
    ('error', 0.021725636250775917)
    ('error', 0.006207324643078833)
    

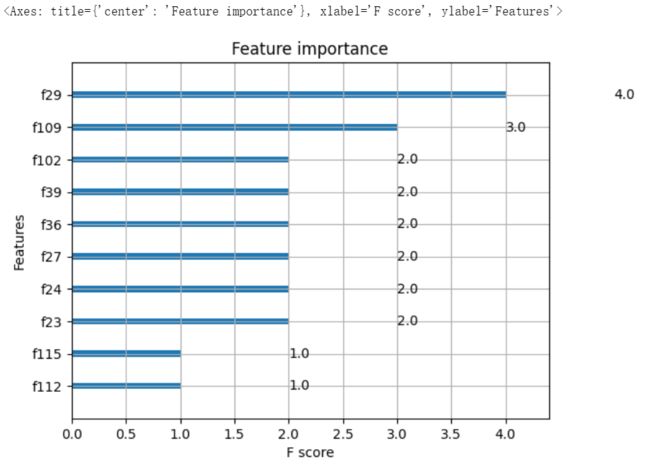
• 绘制特征重要度

  • %matplotlib inline
    from xgboost import plot_importance
    from matplotlib import pyplot as plt
    plot_importance(model, max_num_features=10)
    

  • 

使用sklearn中自带的数据集，如手写数字（10分类问题）、鸢尾花（3分类问题）

• sklearn中的KFold、train_test_split等都可以组合使用，下面xgboost的使用，也主要使用sklearn风格的API，例如xxClassifier，xxRegressor、fit、predict等。

• 导包，加载数据

• import pickle
  import xgboost as xgb
  import numpy as np
  from sklearn.model_selection import KFold, train_test_split, GridSearchCV
  from sklearn.metrics import confusion_matrix, mean_squared_error
  from sklearn.datasets import load_iris, load_digits
  # 10分类问题
  # 用XGBoost建模，用sklearn做评估，这里使用混淆矩阵进行评估
  # 加载数据(手写数字)
  digits = load_digits()
  print(digits.keys())
  y = digits['target']
  X = digits['data']
  print(X.shape) # (1797, 64)
  print(y.shape)
  # K折切分器
  kf = KFold(n_splits=2, shuffle=True, random_state=1234) # 2折
  for train_index, test_index in kf.split(X):
      # 这里model没做任何param的设定，全使用默认值
      xgb_model = xgb.XGBClassifier().fit(X[train_index], y[train_index])
      pred = xgb_model.predict(X[test_index])
      ground_truth = y[test_index]
      print(confusion_matrix(ground_truth, pred))
      print()
  # 3分类问题（鸢尾花）
  iris = load_iris()
  y_iris = iris['target']
  X_irsi = iris['data']
  kf = KFold(n_splits=2, shuffle=True, random_state=1234) # 2折
  for train_index, test_index in kf.split(X_irsi):
      xgb_model = xgb.XGBClassifier().fit(X_irsi[train_index], y_iris[train_index])
      pred = xgb_model.predict(X_irsi[test_index])
      ground_truth = y_iris[test_index]
      print(confusion_matrix(ground_truth, pred))
  ''' boston 房价预测因为涉及种族问题（有一个和黑人人口占比相关的变量B），波士顿房价这个数据集将在sklearn 1.2版本中被移除。
  # 回归问题（boston房价预测）
  boston = load_boston()
  # print(type(boston))
  X_boston = boston['data']
  y_boston = boston['target']
  kf = KFold(n_splits=2, shuffle=True, random_state=1234) # 2折
  for train_index, test_index in kf.split(X_boston):
      # 这里使用回归器：XGBRegressor
      xgb_model = xgb.XGBRegressor().fit(X_boston[train_index], y_boston[train_index])
      pred = xgb_model.predict(X_boston[test_index])
      ground_truth = y_boston[test_index]
      # 回归问题，所以评估换成mse
      print('mse:', mean_squared_error(ground_truth, pred))
      print()
  '''
  

  • dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])
    (1797, 64)
    (1797,)
    [[ 78   0   0   0   0   0   0   0   1   0]
     [  0  90   0   0   0   1   0   0   0   2]
     [  0   1  82   0   0   0   3   0   0   0]
     [  0   0   1  89   0   0   0   1   0   3]
     [  2   0   0   0 101   0   1   2   1   0]
     [  0   0   0   1   0  96   2   0   0   3]
     [  0   3   0   0   1   0  83   0   1   0]
     [  0   0   0   0   1   0   0  86   0   1]
     [  0   6   1   3   0   1   0   0  71   0]
     [  0   0   0   0   1   1   0   5   2  71]]
    [[97  0  0  0  0  1  0  1  0  0]
     [ 0 86  0  1  0  0  1  0  0  1]
     [ 0  0 90  1  0  0  0  0  0  0]
     [ 0  1  0 86  0  1  0  0  1  0]
     [ 0  1  0  0 72  0  0  0  0  1]
     [ 1  0  0  0  0 72  0  0  2  5]
     [ 1  0  0  0  0  1 91  0  0  0]
     [ 0  0  0  0  0  0  0 90  1  0]
     [ 1  2  0  0  0  1  0  2 85  1]
     [ 0  6  0  1  0  1  0  0  1 91]]
    [[25  0  0]
     [ 0 24  1]
     [ 0  0 25]]
    [[25  0  0]
     [ 0 23  2]
     [ 0  1 24]]
    

• 优化超参数-网格搜索

  • import pandas as pd
    import numpy as np
    # california房价预测数据集  ，替代波士顿房价预测数据集
    from sklearn.datasets import fetch_california_housing
    housing_california = fetch_california_housing()
    X = housing_california.data    # data
    y = housing_california.target   # label
    xgb_model = xgb.XGBRegressor()
    # 参数字典
    param_dict = {'max_depth': [2,4,6], # 最大树深
                  'n_estimators': [50, 100, 200]} # 树的棵树
    rgs = GridSearchCV(xgb_model, param_dict)
    rgs.fit(X, y)
    

  • 

  • print(rgs.best_params_)
    

  • {'max_depth': 4, 'n_estimators': 50}
    

• 调整为最优参数重新训练

  • %pip install seaborn
    from sklearn import metrics 
    import matplotlib.pyplot as plt
    import seaborn as sns
    xgb_model_GCV = xgb.XGBRegressor(max_depth=4,n_estimators=50)
    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
    xgb_model_GCV.fit(x_train, y_train)
    #查看标签数据
    train_predict = xgb_model_GCV.predict(x_train)
    test_predict = xgb_model_GCV.predict(x_test)
    ## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
    print('The accuracy of the R2 score is:',metrics.r2_score(y_train,train_predict))
    print('The accuracy of the R2 score is:',metrics.r2_score(y_test,test_predict))
    

  • The accuracy of the R2 score is: 0.8564505816318845
    The accuracy of the R2 scoren is: 0.8005408595359683