JAVA-高频面试题汇总:回溯
前言
为了让小伙伴们更好地刷题,我将所有leetcode常考题按照知识点进行了归纳。
高频题汇总:
JAVA-高频面试题汇总:动态规划
JAVA-高频面试题汇总:字符串
JAVA-高频面试题汇总:二叉树(上)
JAVA-高频面试题汇总:二叉树(下)
JAVA-高频面试题汇总:回溯
接下来还会进行其他模块的总结,有一起在准备暑期实习的JAVA软开伙伴可以一起交流!
小编微信: Apollo___quan
目录
- 机器人的运动范围(剑指)
- 矩阵中的路径(剑指)
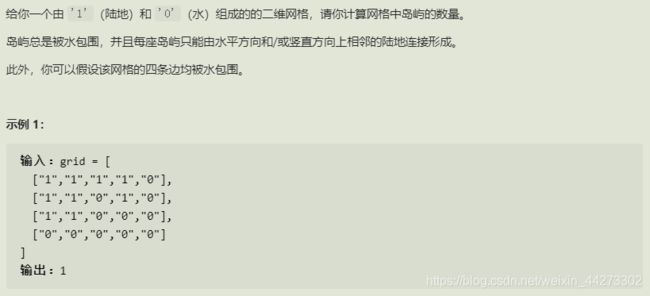
- 岛屿数量
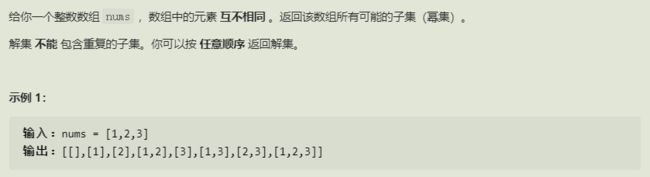
- 子集
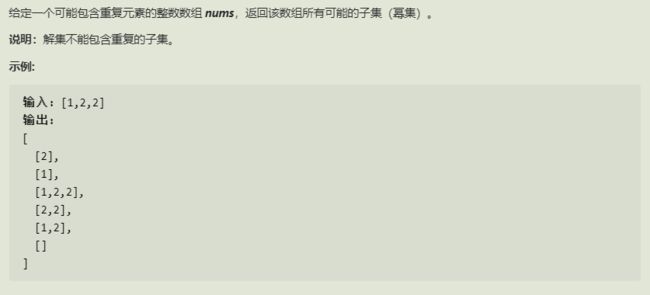
- 子集II
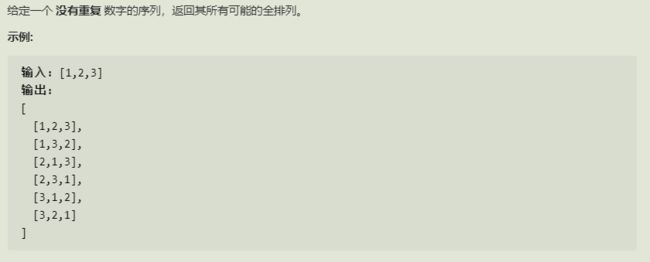
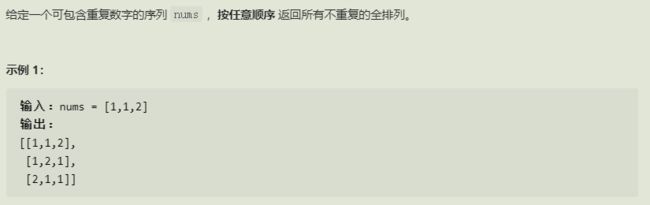
- 全排列
- 全排列II
- 组合总和
- 组合总和II
- 括号生成
1.机器人的运动范围(剑指)
public class Solution {
int m,n,s;
boolean[][] visitor;
public int movingCount(int threshold, int rows, int cols)
{
this.m=rows;this.n=cols;this.s=threshold;
visitor=new boolean[m][n]; //一定要注意这里不要再boolean visitor=new boolean[m][n]
//这样会导致重新声明一个数组而不是用类中的数组,导致dfs方法中visitor没定义大小
return dfs(0,0,0,0);
}
public int dfs(int i,int l, int nh, int nl){
if(nh+nl>s||i>=m||l>=n||visitor[i][l]) return 0;
visitor[i][l]=true;
return 1+dfs(i+1, l, (i+1)%10==0?(nh-8):nh+1, nl)+ dfs(i, l+1, nh, (l+1)%10==0?(nl-8):nl+1);
}
}
2.矩阵中的路径(剑指)
思路
从M*N个点每个点都要作为起点进行寻找,和上一题需要区分的时,每次遍历后,该题被标记走过的单元格需要归还(因为下次遍历是一次全新的遍历)
class Solution {
boolean[][] visitor;
public boolean exist(char[][] board, String word) {
char[] str=word.toCharArray();
int h=board.length, l=board[0].length;
visitor=new boolean[h][l];
for(int i=0; i<h; i++){ //以矩阵每个点为起点
for(int j=0; j<l; j++){
if(recur(board,i,j,0,str)) return true;
}
}
return false;
}
public boolean recur(char[][] board, int i, int j, int k, char[] str){ //k代表了字符串第k个字符
if(i<0||j<0||i>=board.length||j>=board[0].length||(board[i][j] != str[k])||visitor[i][j]) return false;
visitor[i][j]=true;
if(k>=str.length-1) return true;
boolean res = recur(board,i+1,j,k+1,str)||recur(board,i-1,j,k+1,str)||recur(board,i,j+1,k+1,str)||recur(board,i,j-1,k+1,str);
visitor[i][j]=false; //一次遍历后要将单元格归还,因为这道题要从m*n个起点分别开始走,每个单元格都会重复访问
return res;
}
}
3.岛屿数量
思路
1.将矩阵每个点作为起点遍历
2.当前点若为’1’,则置为’0’,然后递归操作紧挨着的’1’
class Solution {
public int numIslands(char[][] grid) {
int count = 0;
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(grid[i][j] == '1'){
dfs(grid, i, j); //代表将这一整块的岛屿都变成了'0'
count++; //岛屿数量++
}
}
}
return count;
}
void dfs(char[][] grid, int i, int j){
if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == '0') return;
grid[i][j] = '0'; //将当前这一块岛屿标记为'0'
dfs(grid, i+1, j); //对上下左右的岛屿进行遍历,将挨着的'1'全变成'0'
dfs(grid, i, j+1);
dfs(grid, i-1, j);
dfs(grid, i, j-1);
}
}
4.子集
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
backtrack(0, nums, res, new ArrayList<Integer>());
return res;
}
private void backtrack(int i, int[] nums, List<List<Integer>> res, ArrayList<Integer> tmp) {
res.add(new ArrayList<>(tmp));
for (int j = i; j < nums.length; j++) {
tmp.add(nums[j]);
backtrack(j + 1, nums, res, tmp);
tmp.remove(tmp.size() - 1);
}
}
}
5.子集 II
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> ans = new ArrayList<>();
Arrays.sort(nums); //排序
getAns(nums, 0, new ArrayList<>(), ans);
return ans;
}
private void getAns(int[] nums, int start, ArrayList<Integer> temp, List<List<Integer>> ans) {
ans.add(new ArrayList<>(temp));
for (int i = start; i < nums.length; i++) {
//和上个数字相等就跳过
if (i > start && nums[i] == nums[i - 1]) {
continue;
}
temp.add(nums[i]);
getAns(nums, i + 1, temp, ans);
temp.remove(temp.size() - 1);
}
}
6.全排列
import java.util.ArrayList;
import java.util.List;
public class Solution {
public List<List<Integer>> permute(int[] nums) {
int len = nums.length;
// 使用一个动态数组保存所有可能的全排列
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
boolean[] used = new boolean[len];
List<Integer> path = new ArrayList<>();
dfs(nums, len, 0, path, used, res);
return res;
}
private void dfs(int[] nums, int len, int depth,
List<Integer> path, boolean[] used,
List<List<Integer>> res) {
if (depth == len) {
res.add(new ArrayList<>(path)); //注意是对path的拷贝
return;
}
// 在非叶子结点处,产生不同的分支,这一操作的语义是:在还未选择的数中依次选择一个元素作为下一个位置的元素,这显然得通过一个循环实现。
for (int i = 0; i < len; i++) {
if (!used[i]) {
path.add(nums[i]);
used[i] = true;
dfs(nums, len, depth + 1, path, used, res);
// 注意:下面这两行代码发生 「回溯」,回溯发生在从 深层结点 回到 浅层结点 的过程,代码在形式上和递归之前是对称的
used[i] = false;
path.remove(path.size() - 1);
}
}
}
public static void main(String[] args) {
int[] nums = {1, 2, 3};
Solution solution = new Solution();
List<List<Integer>> lists = solution.permute(nums);
System.out.println(lists);
}
}
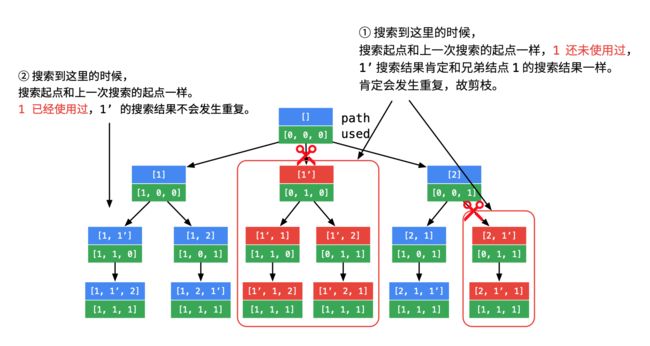
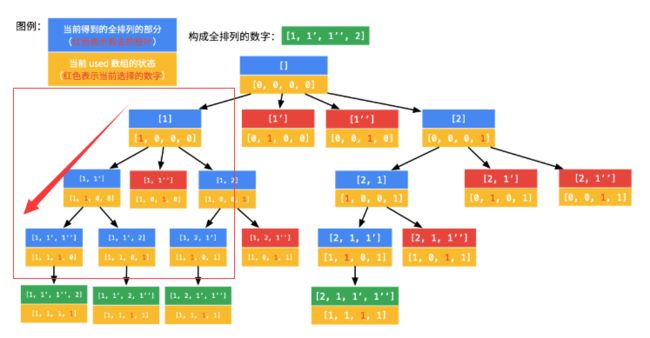
7.全排列 II
思路
子集根据的是begin,考虑的是数字相同与否的问题,把相同的全部跳过即可。
例如[1,2,2,2,3],在第二层,试过了第一个2后跳过之后的2,进入下一层
排列根据的是used[],考虑的是数字在这一层是否出现过的问题,得根据used[i-1]判断和上一个数是不是在同一层,used[i-1]为false则在在一层,跳过
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
int len = nums.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 排序(升序或者降序都可以),排序是剪枝的前提
Arrays.sort(nums);
boolean[] used = new boolean[len];
// 使用 Deque 是 Java 官方 Stack 类的建议
Deque<Integer> path = new ArrayDeque<>(len);
dfs(nums, len, 0, used, path, res);
return res;
}
private void dfs(int[] nums, int len, int depth, boolean[] used, Deque<Integer> path, List<List<Integer>> res) {
if (depth == len) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < len; ++i) {
if (used[i]) {
continue;
}
// 剪枝条件:i > 0 是为了保证 nums[i - 1] 有意义
// 写 !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
path.addLast(nums[i]);
used[i] = true;
dfs(nums, len, depth + 1, used, path, res);
// 回溯部分的代码,和 dfs 之前的代码是对称的
used[i] = false;
path.removeLast();
}
}
}
8.组合总和
什么时候使用 used 数组,什么时候使用 begin 变量
有些朋友可能会疑惑什么时候使用 used 数组,什么时候使用 begin 变量。这里为大家简单总结一下:
排列问题,讲究顺序(即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时),需要记录哪些数字已经使用过,此时用 used 数组。
组合问题,不讲究顺序(即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时),需要按照某种顺序搜索,此时使用 begin 变量。
无枝剪
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
Deque<Integer> path = new ArrayDeque<>();
dfs(candidates, 0, len, target, path, res);
return res;
}
/**
* @param candidates 候选数组
* @param begin 搜索起点
* @param len 冗余变量,是 candidates 里的属性,可以不传
* @param target 每减去一个元素,目标值变小
* @param path 从根结点到叶子结点的路径,是一个栈
* @param res 结果集列表
*/
private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
// target 为负数和 0 的时候不再产生新的孩子结点
if (target < 0) {
return;
}
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
// 重点理解这里从 begin 开始搜索的语意
for (int i = begin; i < len; i++) {
path.addLast(candidates[i]);
// 注意:由于每一个元素可以重复使用,下一轮搜索的起点依然是 i,这里非常容易弄错
dfs(candidates, i, len, target - candidates[i], path, res);
// 状态重置
path.removeLast();
}
}
}
有枝剪
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 排序是剪枝的前提
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>();
dfs(candidates, 0, len, target, path, res);
return res;
}
private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
// 由于进入更深层的时候,小于 0 的部分被剪枝,因此递归终止条件值只判断等于 0 的情况
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < len; i++) {
// 重点理解这里剪枝,前提是候选数组已经有序,
if (target - candidates[i] < 0) {
break;
}
path.addLast(candidates[i]);
dfs(candidates, i, len, target - candidates[i], path, res);
path.removeLast();
}
}
}
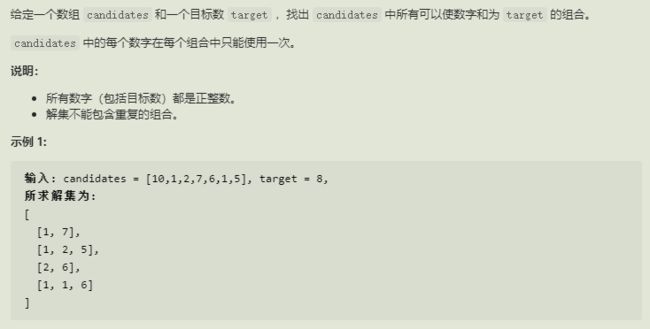
9.组合总和 II
思路
解决这个问题可能需要解决 第 15 题(三数之和)、 第 47 题(全排列 II)、 第 39 题(组合之和)的经验
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 关键步骤
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>(len);
dfs(candidates, len, 0, target, path, res);
return res;
}
/**
* @param candidates 候选数组
* @param len 冗余变量
* @param begin 从候选数组的 begin 位置开始搜索
* @param target 表示剩余,这个值一开始等于 target,基于题目中说明的"所有数字(包括目标数)都是正整数"这个条件
* @param path 从根结点到叶子结点的路径
* @param res
*/
private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < len; i++) {
// 大剪枝:减去 candidates[i] 小于 0,减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0,因此用 break
if (target - candidates[i] < 0) {
break;
}
// 小剪枝:同一层相同数值的结点,从第 2 个开始,候选数更少,结果一定发生重复,因此跳过,用 continue
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
path.addLast(candidates[i]);
// 调试语句 ①
// System.out.println("递归之前 => " + path + ",剩余 = " + (target - candidates[i]));
// 因为元素不可以重复使用,这里递归传递下去的是 i + 1 而不是 i
dfs(candidates, len, i + 1, target - candidates[i], path, res);
path.removeLast();
// 调试语句 ②
// System.out.println("递归之后 => " + path + ",剩余 = " + (target - candidates[i]));
}
}
public static void main(String[] args) {
int[] candidates = new int[]{10, 1, 2, 7, 6, 1, 5};
int target = 8;
Solution solution = new Solution();
List<List<Integer>> res = solution.combinationSum2(candidates, target);
System.out.println("输出 => " + res);
}
}
10.括号生成
思路
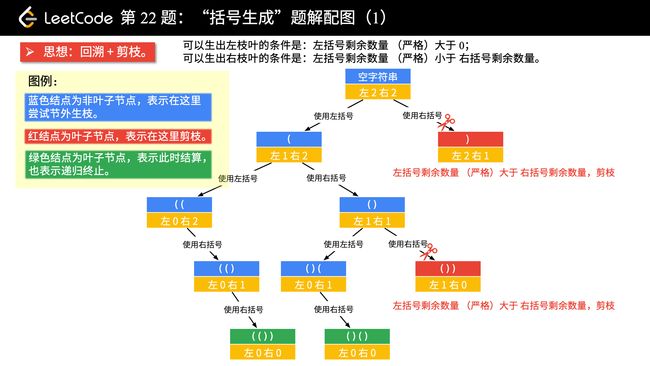
画图以后,可以分析出的结论:
当前左右括号都有大于 0 个可以使用的时候,才产生分支;
产生左分支的时候,只看当前是否还有左括号可以使用;
产生右分支的时候,还受到左分支的限制,右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候,才可以产生分支;
在左边和右边剩余的括号数都等于 0 的时候结算。
算法逻辑:
1.左右都为0,结算
2.左大于右,返回
3.左大于0,左括号来个
4.右大于0,右括号来个
import java.util.ArrayList;
import java.util.List;
public class Solution {
// 做减法
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
// 特判
if (n == 0) {
return res;
}
// 执行深度优先遍历,搜索可能的结果
dfs("", n, n, res);
return res;
}
/**
* @param curStr 当前递归得到的结果
* @param left 左括号还有几个可以使用
* @param right 右括号还有几个可以使用
* @param res 结果集
*/
private void dfs(String curStr, int left, int right, List<String> res) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯
// 在递归终止的时候,直接把它添加到结果集即可,注意与「力扣」第 46 题、第 39 题区分
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
if (left > right) {
return;
}
if (left > 0) {
dfs(curStr + "(", left - 1, right, res);
}
if (right > 0) {
dfs(curStr + ")", left, right - 1, res);
}
}
}
总结
回溯题型整理完毕,其余类型
JAVA-高频面试题汇总:动态规划
JAVA-高频面试题汇总:字符串
JAVA-高频面试题汇总:二叉树(上)
JAVA-高频面试题汇总:二叉树(下)