图像处理实践 | 水果图像的识别与分类
水果图像的识别与分类
1 数据获取与数据集介绍
数据来源:公开水果数据集fruit-360,包含几十种水果的彩色图片,图片格式为100*100像素,训练集中,每种水果都有上百张各种角度拍摄的照片。可以通过对图像的预处理、特征提取,并构建分类器对于水果照片进行分类。
数据集可从Github上下载:https://github.com/Horea94/Fruit-Images-Dataset
2 预处理与特征提取
2.1 相关库的导入
对于图像分类问题,我们使用python-opencv的相关模块来对于图像进行预处理,同时,使用scikit-image来提取图像中的一些特征,这里主要尝试使用HOG (Histogram of Oriented Gridients) 来描述图像中局部纹理特征,分类器我们使用sklearn中的SVM、kNN、决策树等模型。
import numpy as np
import cv2
import glob
import os
import matplotlib.pyplot as plt
import string
from mlxtend.plotting import plot_decision_regions
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.utils.multiclass import unique_labels
from sklearn import metrics
from sklearn.svm import SVC
# HOG
import json
from skimage import color
from skimage.feature import hog
from sklearn import svm
from sklearn.metrics import classification_report,accuracy_score
from subprocess import check_output
dim = 100
2.2 数据集导入
数据集包括多个文件夹,每个文件夹中是同一种水果,这里我们定义一个函数方便我们进行数据导入。
def GetFruit(fruitlist,datatype,print_n=False,k_fold=False):
images=[]
labels=[]
val=['train','test']
if not k_fold:
PATH="E:/kaggle/fruit-360/"+datatype+"/"
for i,fruit in enumerate(fruitlist):
p=PATH+fruit
j=0
for image_path in glob.glob(os.path.join(p,"*.jpg")):
image=cv2.imread(image_path,cv2.IMREAD_COLOR)
image=cv2.resize(image,(dim,dim))
image=cv2.cvtColor(image,cv2.COLOR_RGB2BGR)
images.append(image)
labels.append(i)
j+=1
if(print_n):
print("There are",j,"",datatype.upper()," images of ",fruitlist[i].upper())
images=np.array(images)
labels=np.array(labels)
return images,labels
else:
for v in val:
PATH="E:/kaggle/fruit-360/"+v+"/"
for i,fruit in enumerate(fruitlist):
p=PATH+fruit
j=0
for image_path in glob.glob(os.path.join(p,"*.jpg")):
image=cv2.imread(image_path,cv2.IMREAD_COLOR)
image=cv2.resize(image,(dim,dim))
image=cv2.cvtColor(image,cv2.COLOR_RGB2BGR)
images.append(image)
labels.append(i)
j+=1
images=np.array(images)
labels=np.array(labels)
return images,labels
def GetAll():
fruitlist=[]
for fruit_path in glob.glob("E:/kaggle/fruit-360/train/*"):
fruit=frui_path.split("/")[-1]
fruitlist.append(fruit)
return fruits
同时,我们还希望在图像识别的过程中明白算法中间发生了什么事情,因此可以通过一定的可视化操作来实现这一点,这里定义相关的可视化函数:
def getClassNumber(y):
v =[]
i=0
count = 0
for index in y:
if(index == i):
count +=1
else:
v.append(count)
count = 1
i +=1
v.append(count)
return v
def plotPrincipalComponents(X, dim):
v = getClassNumber(y_train)
colors = 'orange', 'purple', 'r', 'c', 'm', 'y', 'k', 'grey', 'b', 'g'
markers = ['o', 'x' , 'v', 'd']
tot = len(X)
start = 0
if(dim == 2):
for i,index in enumerate(v):
end = start + index
plt.scatter(X[start:end,0],X[start:end,1] , color=colors[i%len(colors)], marker=markers[i%len(markers)], label = fruitlist[i])
start = end
plt.xlabel('PC1')
plt.ylabel('PC2')
if(dim == 3):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i,index in enumerate(v):
end = start + index
ax.scatter(X[start:end,0], X[start:end,1], X[start:end,2], color=colors[i%len(colors)], marker=markers[i%len(markers)], label = fruitlist[i])
start = end
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
plt.legend(loc='lower left')
plt.xticks()
plt.yticks()
plt.show()
# 绘制混淆矩阵
def plot_confusion_matrix(y_true, y_pred, classes,
normalize=False,
title=None,
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if not title:
if normalize:
title = 'Normalized confusion matrix'
else:
title = 'Confusion matrix, without normalization'
# Compute confusion matrix
cm = metrics.confusion_matrix(y_true, y_pred)
# Only use the labels that appear in the data
classes = unique_labels(y_true, y_pred)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
fig, ax = plt.subplots()
im = ax.imshow(cm, interpolation='nearest', cmap=cmap)
ax.figure.colorbar(im, ax=ax)
# We want to show all ticks...
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# ... and label them with the respective list entries
xticklabels=fruitlist, yticklabels=fruitlist,
title=title,
ylabel='True label',
xlabel='Predicted label')
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout()
return cm,ax
2.3 数据查看与编码
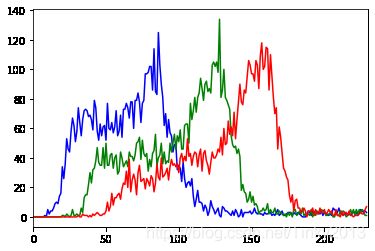
取一张图片,查看其RGB直方图,这一点可以直接由cv模块中的相关函数来完成。从直方图上我们能够看到图像数据的频率分布,便于我们检测图像的明度和色彩的变化趋势。
sample = cv2.imread("E:/kaggle/fruit-360/train/Kiwi/0_100.jpg",cv2.IMREAD_COLOR)
plt.hist(sample.ravel(), bins=256, range=[0, 256]);
plt.show()
color = ('b', 'g', 'r')
for i, col in enumerate(color):
histr = cv2.calcHist([sample], [i], None, [256], [0, 256])
plt.plot(histr, color=col)
plt.xlim([0, 256])
plt.show()
可以看到,图像的曝光程度正常,直方图没有明显偏左或者偏右。同时GRB三条曲线的偏离不是很大,说明白平衡没有较大问题。
为了简单起见,考虑二分类问题,这里我们需要区分菠萝和猕猴桃(选择这两种水果是因为从外表来看颜色比较相似,想要区分不会那么容易)
# Binary classification
fruitlist=['Pineapple','kiwi']
# Get image and Labels
X_train_raw,y_train=GetFruit(fruitlist,'train',print_n=True,k_fold=False)
X_test_raw,y_test=GetFruit(fruitlist,'test',print_n=True,k_fold=False)
# Get data for k-fold
X_raw,y=GetFruit(fruitlist,'',print_n=True,k_fold=True)
将所有图片储存在列表里,接着提取图片的hog特征。HOG先计算图片某一区域中不同方向上梯度的值,然后进行累积,得到直方图,这个特征能够直接输入到分类器当中实现图像分类。
from skimage import feature
ppc=16
hog_features_train = []
hog_features_test = []
hog_images_train= []
hog_images_test=[]
for image in X_train_raw:
fd,hog_image = feature.hog(image, orientations=8, pixels_per_cell=(ppc,ppc),cells_per_block=(4, 4),block_norm= 'L2',visualize=True)
hog_images_train.append(hog_image)
hog_features_train.append(fd)
for image in X_test_raw:
fd,hog_image = feature.hog(image, orientations=8, pixels_per_cell=(ppc,ppc),cells_per_block=(4, 4),block_norm= 'L2',visualize=True)
hog_images_test.append(hog_image)
hog_features_test.append(fd)
# Scale data Images
scaler=StandardScaler()
X_train=scaler.fit_transform([i.flatten() for i in X_train_raw])
X_test=scaler.fit_transform([i.flatten() for i in X_test_raw])
X_train_hog=scaler.fit_transform([i.flatten() for i in hog_images_train])
X_test_hog=scaler.fit_transform([i.flatten() for i in hog_images_test])
X=scaler.fit_transform([i.flatten() for i in X_raw])
There are 490 TRAIN images of PINEAPPLE
There are 466 TRAIN images of KIWI
There are 166 TEST images of PINEAPPLE
There are 156 TEST images of KIWI
可以看到,菠萝的训练集和测试集分别有490、166张图片,猕猴桃的训练集分别有466、156张图片。
print("Shape of the data:")
print((X_train.shape,y_train.shape))
print((X_test.shape,y_test.shape))
print(X_train_hog.shape)
print(X_test_hog.shape)
print("\nData sample:")
print((X_train[0],y_train[0]))
print((X_train_hog[0],y_train[0]))
# x中是数据,每张图片由100*100像素,3条RGB通道构成,一共是30000维的向量构成
# y中是预测结果,二分类中被编码为0和1
Shape of the data:
((956, 30000), (956,))
((322, 30000), (322,))
(956, 10000)
(322, 10000)
Data sample:
(array([-1.35474176, 0.24001185, 0.26975539, ..., 0. ,
0. , 0. ]), 0)
(array([0., 0., 0., ..., 0., 0., 0.]), 0)
编码后的图像每张图片被转化为一个30000维的向量,包括100*100像素点的三个RGB通道,同时我们将0-255的值进行尺度变化,转化为-1至1的浮点数。
# 查看数据样例
def plot_image_grid(images, nb_rows, nb_cols, figsize=(15, 15)):
assert len(images) == nb_rows*nb_cols, "Number of images should be the same as (nb_rows*nb_cols)"
fig, axs = plt.subplots(nb_rows, nb_cols, figsize=figsize)
n = 0
for i in range(0, nb_rows):
for j in range(0, nb_cols):
axs[i, j].axis('off')
axs[i, j].imshow(images[n])
n += 1
print(fruitlist)
plot_image_grid(X_train_raw[0:100], 10, 10)
plot_image_grid(X_train_raw[490:590], 10, 10)
['Pineapple', 'kiwi']
可以看到,数据集中的水果图像有各个角度拍摄的,同时我们也可以把单张图片的原图和提取HOG特征后的图像绘制出来:
plt.imshow(X_train_raw[1])
plt.imshow(hog_images_train[1])
提取HOG特征之后,图像在关键的点位中只剩下了特征向量的部分,这里可以看到图像受到光照、角度、颜色的影响明显变小,这样的特征提取有利于我们对于图像进行分类。
3 构建基本的SVM分类器
使用sklearn模块中的SVM分类器,这里我们将提取特征后的图像X_train_hog输入到分类器当中进行训练,同时基于测试集X_test_hog进行模型效果的测试。
# linear SVM using hog features
svm=SVC(gamma='auto',kernel='linear',probability=True)
svm.fit(X_train_hog,y_train)
y_pred=svm.predict(X_test_hog)
# Evaluation
precision=metrics.accuracy_score(y_pred,y_test)*100
print("Accuracy with SVM: {0:.2f}%".format(precision))
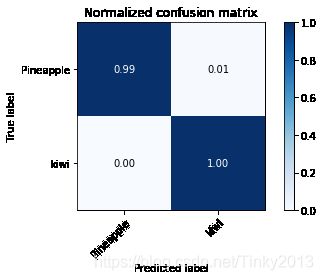
cm,_=plot_confusion_matrix(y_test,y_pred,classes=y_train,normalize=True,title="Normalized confusion matrix")
plt.show()
# calculate FPR and TPR
probs=svm.predict_proba(X_test_hog)
probs=probs[:,1]
svm_fpr,svm_tpr,thresholds=metrics.roc_curve(y_test,probs)
svm_auc=metrics.roc_auc_score(y_test,probs)
Accuracy with SVM: 100.00%
可以看到,将图像提取出的特征用SVM进行分类之后准确率达到了100%,同时我们可以看到在测试集上的混淆矩阵,这说明用这种方法进行分类是相当有效的。
4 更多分类模型的尝试
4.1 使用PCA进行降维
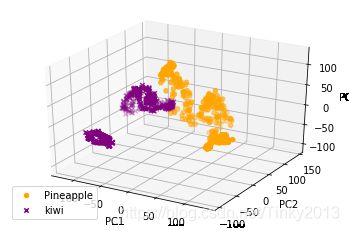
PCA可以通过线性变换,重整高维数据,提取其中的重要部分,忽略其中无关紧要的部分,这里我们使用PCA对于图片进行处理,同时对中间过程进行可视化。
# 使用PCA提取特征
pca = PCA(n_components=3)
dataIn3D = pca.fit_transform(X_train)
plotPrincipalComponents(dataIn3D, 3)
可以看到,两种水果的前三个主成分在空间中的分布有所不同,因此我们可以根据数据点在空间位置的不同来构建分类器。
# 展示PCA内部细节的模块
def showPCA(image,X2, X10, X50):
fig = plt.figure(figsize=(15,15))
ax1 = fig.add_subplot(1,4,1)
ax1.axis('off')
ax1.set_title('Original image')
plt.imshow(image)
ax1 = fig.add_subplot(1,4,2)
ax1.axis('off')
ax1.set_title('50 PC')
plt.imshow(X50)
ax1 = fig.add_subplot(1,4,3)
ax1.axis('off')
ax1.set_title('10 PC')
plt.imshow(X10)
ax2 = fig.add_subplot(1,4,4)
ax2.axis('off')
ax2.set_title('2 PC')
plt.imshow(X2)
plt.show()
def computePCA(n, im_scaled, image_id):
pca = PCA(n)
principalComponents = pca.fit_transform(im_scaled)
im_reduced = pca.inverse_transform(principalComponents)
newImage = scaler.inverse_transform(im_reduced[image_id])
return newImage
def showVariance(X_train):
#Compute manually the principal components
cov_matr=np.dot(X_train, X_train.T)
eigval,eigvect=np.linalg.eig(cov_matr)
index=np.argsort(eigval)[::-1] #take in order the index of ordered vector (ascending order)
#eigvect[:,i] is associated to eigval[i] so
eigvect=eigvect[:,index]
eigval=eigval[index]
n_PC=[]
var_explained=[]
var_temp=[]
var_tmp=0
for i in range(10):
var_tmp=var_tmp+eigval[i]
n_PC.append(i)
var_temp.append(eigval[i]/(eigval.sum())*100)
var_explained.append(var_tmp/(eigval.sum())*100)
fig, ax = plt.subplots(figsize=(8,8))
ind = np.arange(10)
width = 0.35 # the width of the bars
p1 = ax.bar(ind, var_temp, width, color='orange')
p2 = ax.bar(ind + width, var_explained, width, color='blue')
ax.legend((p1[0], p2[0]), ('Individual explained variance', 'Cumulative explained variance'))
ax.set_title('Variance explained using PCs')
ax.set_xticks(ind + width / 2)
ax.set_xticklabels(('1', '2', '3', '4', '5', '6', '7', '8', '9', '10'))
plt.xlabel('Number of PC')
plt.ylabel('Variance exaplained in %')
ax.autoscale_view()
plt.show()
image_id = 2
image = X_train_raw[image_id]
#Compute PCA
X_2 = computePCA(2, X_train,image_id)
X_10 = computePCA(10, X_train,image_id)
X_50 = computePCA(50, X_train,image_id)
#Reshape in order to plot images
X2 = np.reshape(X_2, (dim,dim,3)).astype(int)
X10 = np.reshape(X_10, (dim,dim,3)).astype(int)
X50 = np.reshape(X_50, (dim,dim,3)).astype(int)
#Plot
showPCA(image, X2, X10, X50)
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
可以看到,选取的主成分越少,图像就变得越为抽象,选取的主成分越多,图像就越接近原始的图像,展现的细节也越多。
showVariance(X_train)
4.2 用降维后的数据构建SVM分类器
# SVM modely
svm=SVC(gamma='auto',kernel='linear',probability=True)
svm.fit(X_train,y_train)
y_pred=svm.predict(X_test)
# Evaluation
precision=metrics.accuracy_score(y_pred,y_test)*100
print("Accuracy with SVM: {0:.2f}%".format(precision))
cm,_=plot_confusion_matrix(y_test,y_pred,classes=y_train,normalize=True,title="Normalized confusion matrix")
plt.show()
# calculate FPR and TPR
probs=svm.predict_proba(X_test)
probs=probs[:,1]
svm_fpr,svm_tpr,thresholds=metrics.roc_curve(y_test,probs)
svm_auc=metrics.roc_auc_score(y_test,probs)
Accuracy with SVM: 100.00%
pred_kfold=cross_val_score(svm,X,y,cv=5)
print("Accuracy with SVM and K-FOLD cross validation: %0.2f"%(pred_kfold.mean()))
Accuracy with SVM and K-FOLD cross validation: 0.99
可以看到,PCA降维后再次输入SVM也能保持几乎100%的分类正确率。我们可以画出只选取前两个主成分的PCA降维分类的图像:
pca = PCA(n_components=2)
X_train2D = pca.fit_transform(X_train)
X_test2D = pca.fit_transform(X_test)
svm.fit(X_train2D, y_train)
test_predictions = svm.predict(X_test2D)
precision = metrics.accuracy_score(test_predictions, y_test) * 100
print("Accuracy with SVM considering only first 2PC: {0:.2f}%".format(precision))
#Plotting decision boundaries
plot_decision_regions(X_train2D, y_train, clf=svm, legend=1)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('Linear SVM Decision Boundaries')
plt.show()
Accuracy with SVM considering only first 2PC: 98.14%
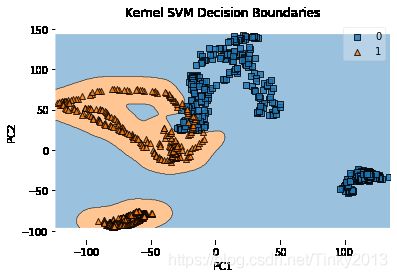
另外也可以尝试使用核PCA:
svm_with_kernel = SVC(gamma=0.01, kernel='rbf', probability=True)
svm_with_kernel.fit(X_train2D, y_train)
y_pred = svm_with_kernel.predict(X_test2D)
precision = metrics.accuracy_score(y_pred, y_test) * 100
print("Accuracy with Not-Linear SVM considering only first 2PC: {0:.2f}%".format(precision))
#Plotting decision boundaries
plot_decision_regions(X_train2D, y_train, clf=svm_with_kernel, legend=1)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('Kernel SVM Decision Boundaries')
plt.show()
Accuracy with Not-Linear SVM considering only first 2PC: 64.91%
可以看到使用rbf核的PCA在测试集的准确率不及线性核,从图像中也可以看出,实现分类的并不是一条直线,而是不规则的边界。
4.3 使用kNN分类器
# knn
knn = KNeighborsClassifier(n_neighbors=2)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
#Evaluation
precision = metrics.accuracy_score(y_pred, y_test) * 100
print("Accuracy with K-NN: {0:.2f}%".format(precision))
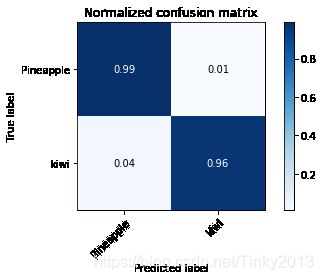
cm , _ = plot_confusion_matrix(y_test, y_pred, classes=y_train, normalize=True, title='Normalized confusion matrix')
plt.show()
# calculate the FPR and TPR for all thresholds of the classification
probs = knn.predict_proba(X_test)
probs = probs[:, 1]
knn_fpr, knn_tpr, thresholds = metrics.roc_curve(y_test, probs)
knn_auc = metrics.roc_auc_score(y_test, probs)
Accuracy with K-NN: 99.69%
#KNN + K-FOLD
pred_kfold = cross_val_score(knn, X, y, cv=5)
print("Accuracy with K-NN and K-FOLD CROSS VALIDATION: %0.2f " % (pred_kfold.mean()))
Accuracy with K-NN and K-FOLD CROSS VALIDATION: 0.97
可以看到,kNN分类器能够达到99%的精度,同理,也可以将决策边界给画出来从而理解数据本身:
#K-NN + PCA
knn.fit(X_train2D, y_train)
y_pred = knn.predict(X_test2D)
precision = metrics.accuracy_score(y_pred, y_test) * 100
print("Accuracy with K-NN considering only first 2PC: {0:.2f}%".format(precision))
#Plotting decision boundaries
plot_decision_regions(X_train2D, y_train, clf=knn, legend=1)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('K-NN Decision Boundaries')
plt.show()
Accuracy with K-NN considering only first 2PC: 98.14%
4.4 决策树分类器
tree = DecisionTreeClassifier()
tree = tree.fit(X_train,y_train)
y_pred = tree.predict(X_test)
#Evaluation
precision = metrics.accuracy_score(y_pred, y_test) * 100
print("Accuracy with Decision Tree: {0:.2f}%".format(precision))
cm , _ = plot_confusion_matrix(y_test, y_pred, classes=y_train, normalize=True, title='Normalized confusion matrix')
plt.show()
# calculate the FPR and TPR for all thresholds of the classification
probs = tree.predict_proba(X_test)
probs = probs[:, 1]
tree_fpr, tree_tpr, thresholds = metrics.roc_curve(y_test, probs)
tree_auc = metrics.roc_auc_score(y_test, probs)
Accuracy with Decision Tree: 97.52%
#DECISION TREE + K-FOLD
pred_kfold = cross_val_score(tree, X, y, cv=5)
print("Accuracy with DECISION TREE and K-FOLD CROSS VALIDATION: %0.2f" % (pred_kfold.mean()))
Accuracy with DECISION TREE and K-FOLD CROSS VALIDATION: 0.95
可以看到,使用决策树分类器能够达到95%精确率,我们也能将决策边界绘制出来:
#DECISION TREE + PCA
tree = tree.fit(X_train2D,y_train)
y_pred = tree.predict(X_test2D)
precision = metrics.accuracy_score(y_pred, y_test) * 100
print("Accuracy with Decision Tree considering only first 2PC: {0:.2f}%".format(precision))
#Plotting decision boundaries
plot_decision_regions(X_train2D, y_train, clf=tree, legend=1)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('Decision Tree Decision Boundaries')
plt.show()
Accuracy with Decision Tree considering only first 2PC: 97.52%
参考文章(kernel):
Training svm classifier with hog features. (Manik Galkissa)
Fruit Classification: PCA, SVM, KNN, Decision Tree. (Walter Maffione)