【算法·笔记】LCA最近公共祖先，倍增法

描述

现在给出一颗树，求两点间的最短距离。且，最短距离的这条线路仅此存在唯一的一条线路。

洛谷题目链接：https://www.luogu.com.cn/problem/P3379
OI-WIKI的链接：https://oi-wiki.org/graph/lca

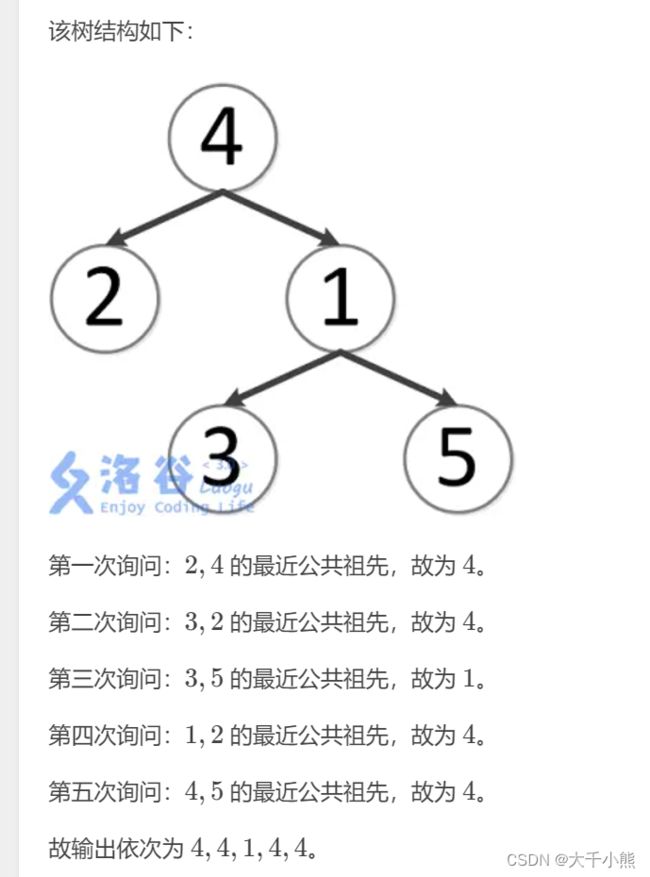
洛谷的描述如上，用于理解概念“最近公共祖先”这样的名词。

思想

现在给出（x，y）求LCA（x，y）。
定义【深度】：离根节点的距离，根开始距离是1，根的子节点距离是2；
有一个很简单的方法，来求解，自然而然的想法是
（1）先把y节点和x节点，一起寻找一个深度相同的节点。
（2）如果通过（1）找到的节点是同一个节点，那么就找到了公共祖先，否则的话，就每一次开始减少深度，继续往根的方向，如果找到了相同的节点，那么就结束。最近的公共祖先被成功的找到了。

倍增的思路

首先来看一个小问题：
现在假设有1000个台阶
我们有两种方式去爬台阶：
（1）每一次走1个台阶。
（2）第一次走$2^{10}$，第二次走走$2^9$，第三次走$2^8$…（也就是用二进制来表示1000的意思）
通过发现，很明显（2）的走的次数要少很多。因为每一次走的都要比（1）相等或者更大一些。

然而，我们知道任何一个十进制的数字，可以表现为二进制，二进制的每一位1，就代表着2的幂次方是几。这点和快速幂是一致的，所以通过构造一个数组，来决定跳转的下一个二进制位是多少。

例如，fa[x][i]代表着，x节点的第$2^i$父亲节点。构造这样一个数组，就可以不用每一次走一步来判断父亲节点。而是我们跳跃着去寻找父亲节点。

int lca(int ix, int iy) {
	if (dep[ix] > dep[iy]) swap(ix, iy); // 保证iy的深度要大于ix的深度
	int h = dep[iy] - dep[ix];
	for (int j = 0; h > 0; ++j, h >>= 1) { // 然后就像上面说的方法（2）一样，通过二进制来开始跳转，使得iy的深度和ix一样
		if (h & 1 == 1) iy = fa[iy][j];
	}
	if (iy == ix) return ix;
	// 。。。。省略。。。。
	return fa[iy][0];
}

然后现在ix和iy深度是一样的，那么我们怎么调整现在深度一样的ix和iy把他们搞成ix==iy并且，这个ix和iy还是lca（最近的公共祖先）呢。

假设我们的最近公共祖先的升读是H，那么现在的这个跳转距离应该是，H-dep[ix]（iy也行，因为经过上面代码，现在dep[ix]==dep[iy]）。好，所以我们令这个H-dep[ix]为Dis。
这个Dis是一个十进制，我们需要通过每一位去猜测，这个Dis的样子。

我们从最高位开始，（所以肯定找到的数字会比Dis大），如果现在fa[ix][j] != fa[iy][j]。那么就有一点可以说明，那就是现在的dep[ix]>dep[Dis]（这是很好证明的，因为父亲节点不相同了，也就说明，现在在分叉的分叉开的那个部分，总之，画图理解一下）。这就说明。我们的猜测相比于Dis要小了。所以现在考虑下一个二进制位，然后再来猜测，这样的跳转能不能成功。

最后，找到的还是fa[ix][j] != fa[iy][j]。但是我们可以肯定，lca就是fa[ix][0]。因为通过猜测位，我们已经把ix和iy逼到最近的lca位置上了。所以，再往前走一步，就OK。

	for (int j = 30; j >= 0 && iy != ix; j--) { // 猜测二进制的位置
		if (fa[ix][j] != fa[iy][j]) { // 调整ix和iy，不停的往前
			ix = fa[ix][j], iy = fa[iy][j];
		}
	}

完整代码参考如下：

// LCA最大公共祖先模板
#include 
using namespace std;
const int MXN = 5 * 1e5 + 5;
int N, M, S, iptx, ipty;
vector<int> v[MXN];
int fa[MXN][32], dep[MXN];
void dfs(int root, int faIndex) {
	fa[root][0] = faIndex;
	dep[root] = dep[faIndex] + 1;
	for (int i = 1; i <= 30; i++) {
		fa[root][i] = fa[fa[root][i - 1]][i - 1];
	}
	int sz = v[root].size();
	for (int i = 0; i < sz; i++) {
		if (v[root][i] == faIndex) continue;
		dfs(v[root][i], root);
	}
}
int lca(int ix, int iy) {
	if (dep[ix] > dep[iy]) swap(ix, iy);
	int h = dep[iy] - dep[ix];
	for (int j = 0; h > 0; ++j, h >>= 1) {
		if (h & 1 == 1) iy = fa[iy][j];
	}
	if (iy == ix) return ix;
	for (int j = 30; j >= 0 && iy != ix; j--) {
		if (fa[ix][j] != fa[iy][j]) {
			ix = fa[ix][j], iy = fa[iy][j];
		}
	}
	return fa[iy][0];
}
int main() {
	memset(fa, 0, sizeof(fa));
	scanf("%d %d %d", &N, &M, &S);
	for (int i = 0; i < N - 1; i++) {
		scanf("%d %d", &iptx, &ipty);
		v[iptx].push_back(ipty);
		v[ipty].push_back(iptx);
	}
	dfs(S, 0);

	for (int i=0; i<M; i++) {
		scanf("%d %d",&iptx,&ipty);
		printf("%d\n",lca(iptx,ipty));
	}

	return 0;
}

蓝桥杯题目补充

——————
Update 2023 4 6
这是一道蓝桥杯的LCA模板题目，其实也挺简单的。
注意进行LCA倍增的时候，更新答案，要及时去除重复的数字，保证答案的正确性。

链接： https://www.luogu.com.cn/problem/P8805

代码

#include
using namespace std;
const int MXN = 5 * 1e5 + 5;
int n,m,ipx,ipy;
vector<int> v[MXN];
int fa[MXN][35],cost[MXN][35],wi[MXN],dep[MXN];
void dfs(int pos,int faIdx) {
	fa[pos][0] = faIdx;
	if (pos!=1) {
		cost[pos][0] = wi[pos]+wi[faIdx];
	}
	dep[pos] = dep[faIdx]+1;
	for (int i=1; i<=30; i++) {
		fa[pos][i] = fa[fa[pos][i-1]][i-1];
		cost[pos][i] = cost[pos][i-1]+cost[fa[pos][i-1]][i-1]-wi[fa[pos][i-1]];
	}
	int sz = v[pos].size();
	for (int i=0; i<sz; i++) {
		if (v[pos][i] == faIdx) continue;
		dfs(v[pos][i],pos);
	}
}
int lca(int ix,int iy) {
	if (ix == iy) return wi[ix];
	int ans=0;
	if (dep[ix]>dep[iy]) swap(ix,iy);
	int h = dep[iy] - dep[ix],lastWiY = 0;
	for (int j = 0; h>0; ++j,h>>=1) {
		if (h&1) {
			ans+=cost[iy][j]-lastWiY;
			iy = fa[iy][j];
			lastWiY = wi[iy];
		}
	}
	if (ix == iy) return ans;
	int lastWiX=0;
	for (int j=30; j>=0&&ix!=iy; j--) {
		if (fa[ix][j]!=fa[iy][j]) {
			ans+=cost[ix][j]-lastWiX + cost[iy][j]-lastWiY;
			ix = fa[ix][j],iy = fa[iy][j];
			lastWiX = wi[ix],lastWiY = wi[iy];
		}
	}
	ans+=cost[ix][0]-lastWiX + cost[iy][0]-lastWiY;
	ix = fa[ix][0];
	ans-=wi[ix];
	return ans;
}
int main() {
	scanf("%d %d",&n,&m);
	for (int i=0; i<n-1; i++) {
		scanf("%d %d",&ipx,&ipy);
		v[ipx].push_back(ipy);
		v[ipy].push_back(ipx);
	}
	for (int i=1; i<=n; i++) wi[i] = v[i].size();
	dfs(1,0);
	for (int i=0; i<m; i++) {
		scanf("%d %d",&ipx,&ipy);
		printf("%d\n",lca(ipx,ipy));
	}
	return 0;
}