数组切分 （蓝桥杯）爆搜，剪枝 JAVA
目录
- 题目描述：
- 暴力破解 ：
-
- dfs + 回溯（void类型）：
- 纯 dfs (int类型)：
- dfs + 备忘录（满分）：
-
- int类型实现：
- void类型实现：
- 思考dfs + 回溯与 纯 dfs（int类型）的区别 ：
- 小结：
题目描述：
已知一个长度为N的数组：A1, A2, A3,…, AN 恰好是1…N 的一个排列。
现在要求你将A数组切分成若干个(最少一个，最多N个) 连续的子数组， 并且每个子数组中包含的整数恰好可以组成一段连续的自然数。
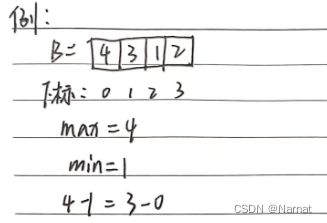
例如对于A={1,3,2,4}存在5种切分方法。
1、{1}{3}{2}{4}
2、{1}{3,2}{4}
3、{1}{3,2,4}
4、{1,3,2}{4}
5、{1,3,2,4}
输入格式：
第一行包含一个整数N。
第二行包含N个整数，代表A数组。
对于30% 评测用例，1≤N≤20。
对于100% 评测用例，1≤N≤10000。
输出格式：
输出一个整数表示答案。 由于答案可能很大，
所以输出其对1000000007取模后的值。
输入样例：
4
1 3 2 4
输出样例：
5
暴力破解 ：
解题思路：
秉承“万物皆可爆搜”的信念，本题我们继续利用爆搜来混分。
1.首先对于题目给出的例子我们得有一个系统的解题方法（也就是咱得先会做，找到规律，再让电脑做。）：
对题目给的例子进行分析如下：
不难发现，这完全就是一颗递归树。其中每一层都对应每层递归内部的 for 循环，每一条路径都对应着一个符合题目要求的切分方法。
(还有一点就是我们可以看到，每一层 for 循环内的子数组都互不影响，所以这需要用到回溯。)
2.如判断某子数组内的整数，恰好可以组成一段连续自然数？
这里给出一个技巧：
子数组最大元素值 - 子数组最小元素值 = 子数组最大下标 - 子数组最小下标
即： max - min = j - i
若此等式成立，则子数组内整数恰好可以组成一段连续自然数。
由于数组内元素不能重复，所以上述等式是成立的。
3.解决完上述问题我们就需要贴合，dfs + 回溯 的模式，将答案爆搜出来。
理论成立代码如下：
dfs + 回溯（void类型）：
import java.util.Scanner;
public class Main {
public static int n = 0;
public static int a[];//放在这里等会写函数就不用调用
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n = sc.nextInt();//注意别写成 int n
a = new int[n];
for(int i = 0; i < n; i ++) a[i] = sc.nextInt();
dfs(0);//从第一个元素开始
System.out.print(sum % 1000000007);//输出答案
}
public static int sum = 0;
public static int max = Integer.MIN_VALUE;
public static int min = Integer.MAX_VALUE;
public static void updatave(int x, int y){//找到区间内最大值与最小值
for(int i = x; i <= y; i ++) {
max = Math.max(max, a[i]);
min = Math.min(min, a[i]);
}
}
public static void default_state(){//将max，min 恢复默认状态
max = Integer.MIN_VALUE;
min = Integer.MAX_VALUE;
}
public static void dfs(int i) {
if(i == n) sum ++;//重要的事情最先做，不能写 成n - 1，否者以j = n - 1结尾的情况不会被记录
for(int j = i; j < n; j ++) {//本身也是一个最小连续子区间，所以从本身开始
updatave(i, j);
if(max - min == j - i) {//满足连续子区间
default_state();//max，min要恢复默认状态，防止影响下面的递归操作
dfs(j + 1);
default_state();//运行完也要恢复默认状态，防止影响 j = i + 1的循环
}
}
}
}
本代码在官方平台上能能拿到五成分数，感觉能混到这么多还是不错的，一直以为只能得三成分数。
纯 dfs (int类型)：
import java.util.Scanner;
public class Main {
public static int mod = 1000000007;
public static int n = 0;
public static int a[];
public static int memo[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
a = new int[n];
for(int i = 0; i < n; i ++) {
a[i] = sc.nextInt();
}
System.out.print(dfs(0));
}
public static int dfs(int index) {
if(index == n) return 1;//到达末端返还1
int sum = 0;
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = index; i < n; i ++) {
max = Math.max(max, a[i]);
min = Math.min(min, a[i]);
if(max - min == i - index) {
sum = (sum + dfs(i + 1)) % mod;//将符条件的加起来
}
}
return sum;
}
}
dfs + 备忘录（满分）：
解题：
创作灵感来源于一个低调的大佬，今天一位大佬跟我分享了他的 dfs + 备忘录代码，焯 ！只能说写的太优雅了！
由于我用暴力用的太久了，默认暴力只能拿一部分分数，今天大佬的代码给我狠狠的打醒了，即可以对 dfs 生成的递归树，通过这种使用备忘录的方法，达到剪枝的效果。
由于我有幸之前懵懂时期在力扣中学过备忘录，再加上大哥的代码足够简洁，我侥幸的能在这么短的时间明白其中原理，只能说相见恨晚，上正题：
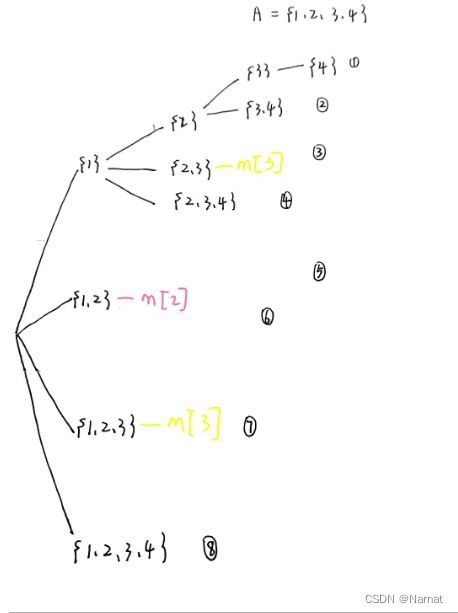
以 A= {1，2， 3， 4} 为例：
按题目要求生成的递归树如下：
上图递归树，每层都是一个新的递归内容，本层内每个枝节都对应着整个 for 循环的每种情况：
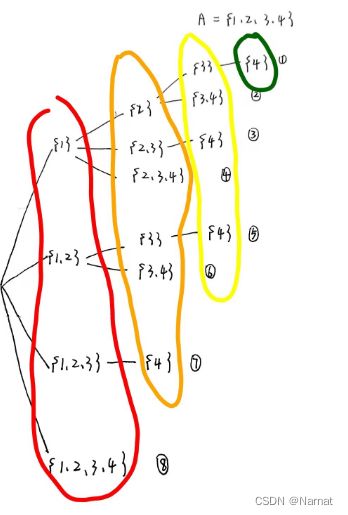
对上述递归树简要观察不难发现：
如上图所示，蓝色矩形区域，和红色圆圈区域都有重复，正是这些重复部分消耗了额外的无效时间，导致超时，引入备忘录的作用就是记录这些值，以便在下次遇见，就不必再次计算，也就是空间换时间。如下：
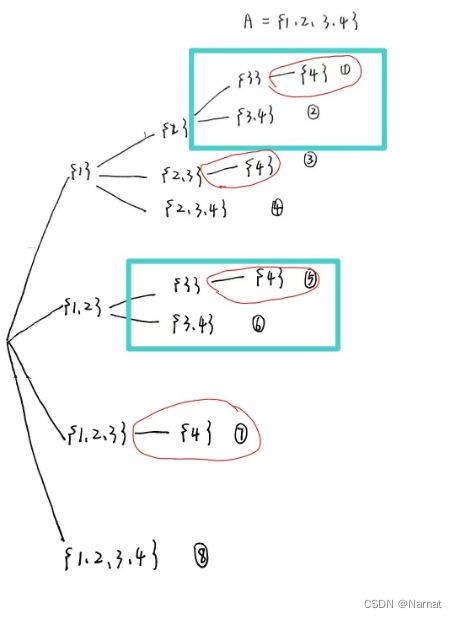
如上，将第一次出现的蓝色矩形和红色圆圈部分记录下来，下方再次出现直接调用memo备忘录即可：
如上图就是剪枝后的递归树
明白上述样例，代码就很清晰了
由于我一直用的void类型大哥给的int类型。
所以以下给出两种类型的dfs方法可按喜好选择：
int类型实现：
import java.util.*;
public class Main {
public static int mod = 1000000007;
public static int n = 0;
public static int a[];
public static int memo[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
a = new int[n];
memo = new int[n + 1];
for(int i = 0; i < n; i ++) {
a[i] = sc.nextInt();
memo[i] = -1;//初始化
}//记忆数组 焯！ 太妙了。
//注意下标从0开始
memo[n] = 1;//n越界，说明得到一个方式，返回1。
System.out.print(dfs(0));
//上下等效。
// dfs(0);
// System.out.print(memo[0]);
}
public static int dfs(int starIndex) {
if(memo[starIndex] != - 1) return memo[starIndex];
int sum = 0;
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int j = starIndex; j < n; j ++) {
max = Math.max(max, a[j]);
min = Math.min(min, a[j]);
if(max - min == j - starIndex) {
sum = (sum + dfs(j + 1)) % mod;
}
}
memo[starIndex] = sum;//存
return sum;//返还本层递归的结果
}
}
void类型实现：
import java.util.Scanner;
public class Main {
public static int mod = 1000000007;
public static int n = 0;
public static int a[];
public static int memo[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
a = new int[n];
memo = new int[n + 1];
for(int i = 0; i < n; i ++) {
a[i] = sc.nextInt();
memo[i] = -1;
}
memo[n] = 1;
dfs(0);
System.out.print(memo[0]);
}
public static void dfs(int starIndex) {
int sum = 0;
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int j = starIndex; j < n; j ++) {
max = Math.max(max, a[j]);
min = Math.min(min, a[j]);
if(max - min == j - starIndex) {
if(memo[j + 1] == -1)//查看备忘录
dfs(j + 1);
sum = (sum + memo[j + 1]) % mod;
}
}
memo[starIndex] = sum;//存
}
}
思考dfs + 回溯与 纯 dfs（int类型）的区别 ：
dfs + 回溯：
将一条路走到尾，在终点计数，再回溯，找其他可行路径。
纯dfs (int 类型)：
从递归末端，将可行路径数量，传递到上一层递归，再由上层递归传输至上上层递归，类似大树按次序用所有的根吸收水分，传递到树干的过程。
小结：
如果问我为什么不用动态规划写正解呢，还是基于实际情况考虑。
1，是我动态规划，只学了背包九讲，只是初步了解，让我不看解析去做这道题，我是真打死不会。
2，是动态规划，也是基于爆搜的前提下去，剪切掉多余的重复部分而逐渐得到的最优解法，如果爆搜都并不会的话，想直接写出动态规划，就好似孩子走路都没学会，就让他跑一样牵强。
这里给出大佬，对递归和动态规划区别的看法：
动态规划是递推，从小问题扩展到大问题。而dfs解决这种问题的方式是递归，先是将大问题抛出，然后不断的将问题变小，最后来解决的大问题。
3，是我目前编程水平比较一般，最擅长的还是爆搜，赛场上用爆搜混到目前这些分数已经是超长发挥了，可以磕头烧香了。当然后期用动态规划如何剪枝这道题我也会去学习的，但前提得先把爆搜学好，毕竟用爆搜解这道题我都想了半天更何况动态规划，而且蓝桥杯快到了。。。。
最后，水平高的大佬可以看看别人的dp解法，如果这个爆搜方法还有可以优化的地方也欢迎大佬们指点。
