数组--二分查找 专题训练

一、数组

1.1 二分查找

704. 二分查找
题目：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

分析：
这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

二分法第一种写法
第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

Go语言

// 第一种方法：
func search(nums []int, target int) int {
        left :=0
        right:=len(nums)-1
        for left<=right{   //左闭右闭的类型
            mid := left+(right-left)/2

            if nums[mid]==target{
                 return mid
            } else if nums[mid]<target{
                left=mid+1
            }else if nums[mid]>target {
                right =mid-1
            }
        }//执行完一遍数组后还没有发现相等的，则返回-1
         return -1
}

二分法第二种写法
如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

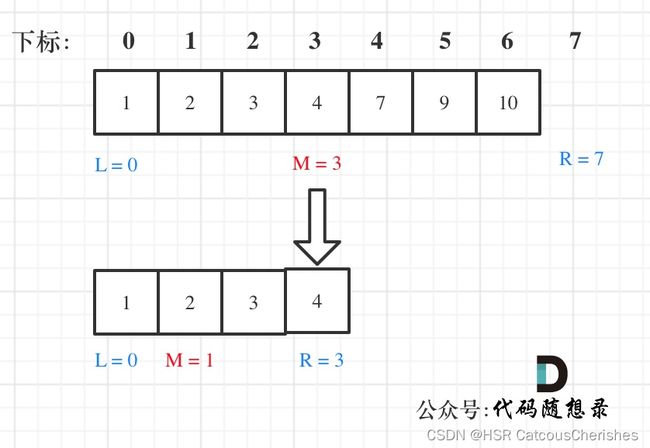
Go 的第二种方法：

func search(nums []int, target int) int {
        left :=0
        right:=len(nums)
        for left<right{   //左闭右开 的类型
            mid := left+(right-left)/2

            if nums[mid]==target{
                 return mid
            } else if nums[mid]<target{
                left=mid+1
            }else if nums[mid]>target {
                right =mid
            }
        }//执行完一遍数组后还没有发现相等的，则返回-1
         return -1
}

相关题目推荐

35.搜索插入位置(opens new window)
34.在排序数组中查找元素的第一个和最后一个位置(opens new window)
69.x 的平方根
367.有效的完全平方数

1.2 其他语言版本

python 第一种方法：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
       left,right =0,len(nums)-1 #  定义target在左闭右闭的区间里，[left, right]
       while left<=right:
           mid =left + (right-left)//2
           if nums[mid]<target:  # target在左区间，所以[middle+1,right]
                left =mid+1
           elif nums[mid]>target:  # target在左区间，所以[left, middle - 1]
                right=mid-1
           elif nums[mid]==target:
                return mid   # 数组中找到目标值，直接返回下标
       return -1   # 未找到目标值

相关推荐：
35. 搜索插入位置（简单）

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

GO语言第一种方案：

func searchInsert(nums []int, target int) int {
    left:=0
    right :=len(nums)-1
    
    if nums[left]>target{ //目标值在数组所有元素之前
        return 0
    }
    if nums[right]<target{//目标值在数组所有元素之后 
    }

    for left<=right{
        mid :=left +(right-left)/2
        if nums[mid]==target{
            // 1. 目标值等于数组中某一个元素  return mid;
              return mid
        }else if nums[mid]<target{
            left =mid+1
        }else if nums[mid]>target {
            right=mid-1
        }
    }
    //2.目标值在数组所有元素之前
    //3.目标值插入数组中 
    //4.目标值在数组所有元素之后   return right + 1;

   return left //目标值插入数组中 

}