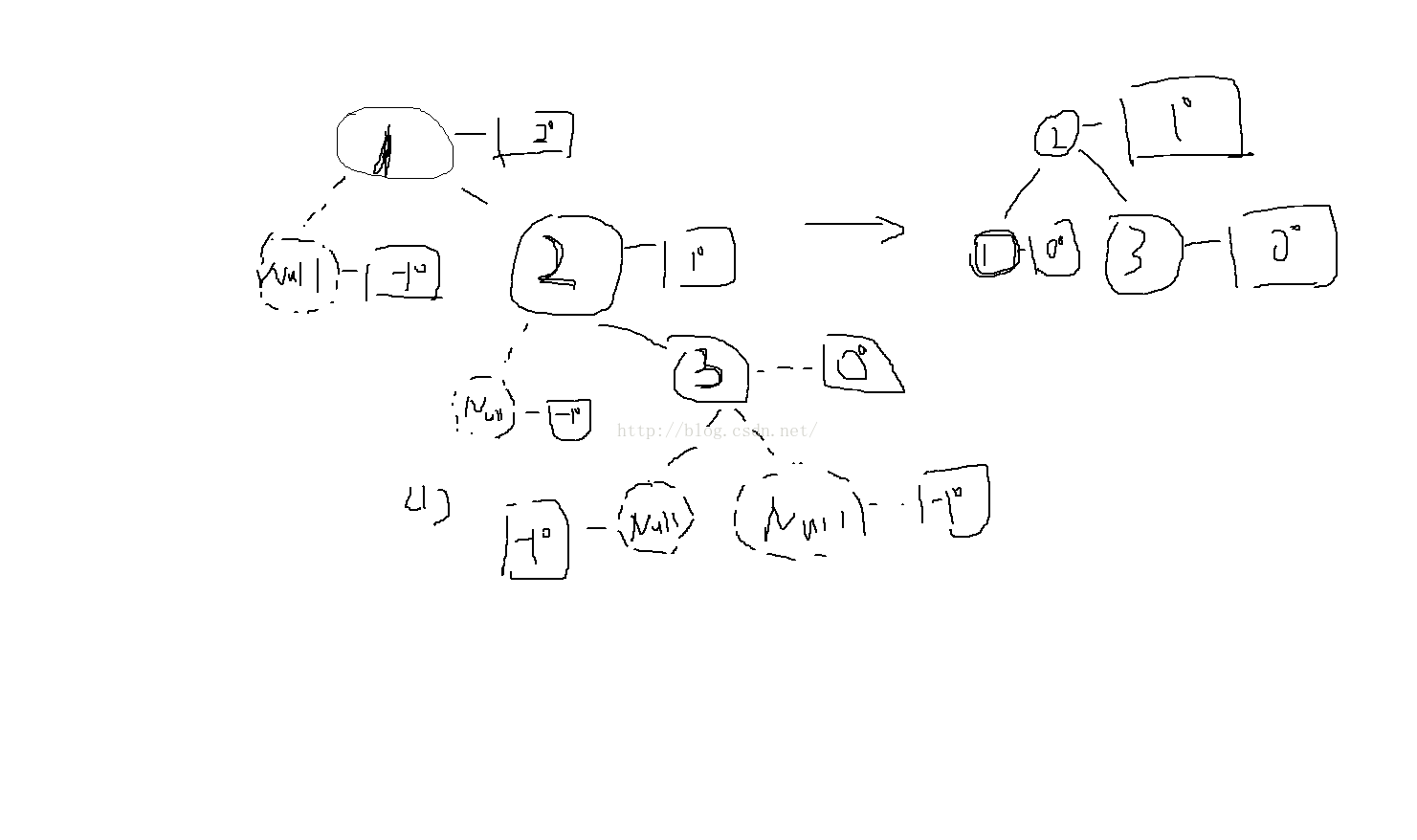AVL平衡二叉树的c++实现

AVL平衡树是对二叉查找的改进，主要是避免而二叉查找树退化成链表，从而导致查找效率出现n的状况。该平衡树由G.M. Adelson-Velsky 和 E.M. Landis法发明，因此成为AVL平衡树。该树定义了一个平衡因子，例如，当同层的两个节点的深度差值大于1以上，则此时需要调整树种的节点，重新调整回到同层的节点深度不超过1的情况。

（1）二叉查找树的退化，下图左边就是一个退化的二叉查找树，由于2大于1，因此2在1的右边，3又大于2，因此3在2的右边，此时如果需要查询3的话，则需要遍历树种的所有节点1,2，3，查找效率为o(n)，而图的右边为左图经过旋转形成一个平衡二叉树。此时，如果查找节点3，只需要遍历节点2和3，即可，查找效率为o(logn)。

（2）从下图，我们也可以看到，在对二叉树进行调整，变成二叉查找树时，相对于二叉树平衡树的构建，需要为每个节点添加上高度信息。该信息主要负责判定什么时候树已经违反平衡树的要求。因此，我们从下往上定义节点的高度信息，当节点为NULL，该节点的高度信息为-1；当节点左右子节点都为NULL时，该节点的高度为0；父节点的高度比子节点的最大高度高1。具体例子，可以参考下图，例如节点1的高度为2度，在节点右侧的方框中显示；节点2的高度为1度。

（3）当判断同层节点的高度相差超过1时，需要旋转树节点来生成avl平衡树，此时，该如何旋转树很关键？此时需要根据树的形状来确定。

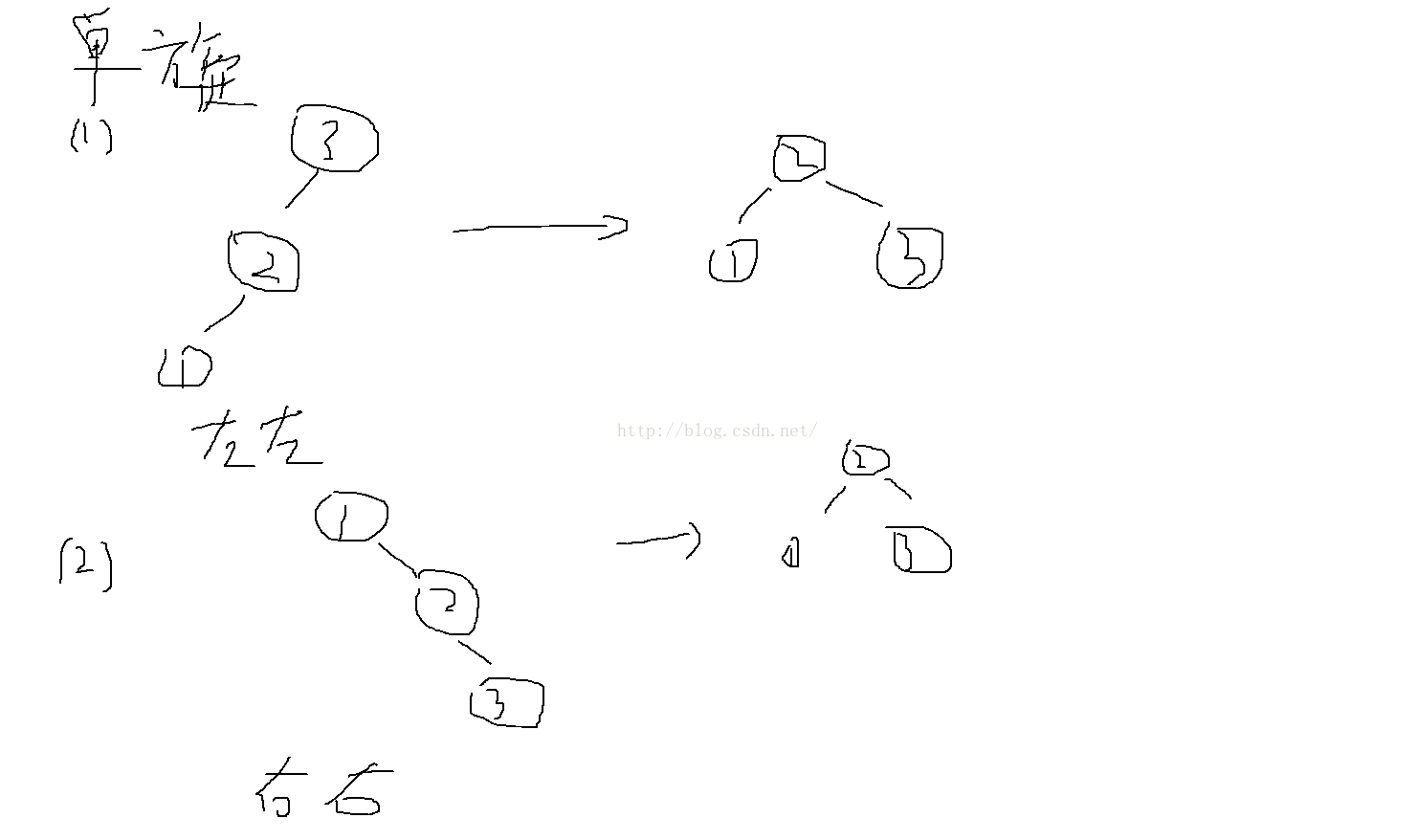
（3.1）单旋转情况，如下图所示。图（1）为左左的情况，图（2）为右右的情况。在图（1）中，我们可以看到节点3的左子节点2的高度为1，而同层的节点3的右子节点为NULL，该节点高度为-1，此时，这两个处于同一层中的两节点的高度相差大于1（等于2），此时需要对节点进行旋转，也就是，将2作为树的新根，1作为2的左节点，3作为2的右节点。旋转后的结果，就能够满足平衡树的要求。图（2）恰好是图（1）的对称情况。

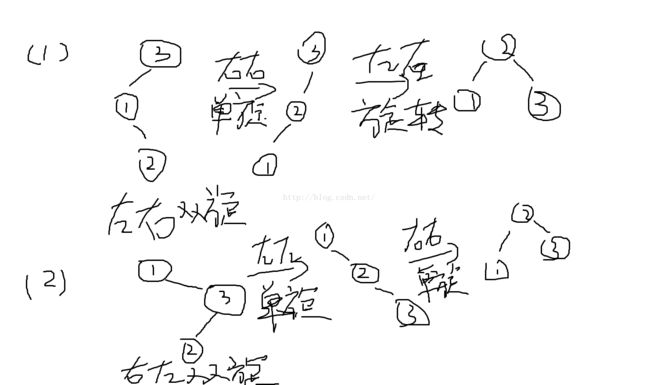
（3.2）双旋转情况。需要对树节点，进行两次的单旋转操作，如下图所示。图（1）为左右双旋。具体操作，先进行右右单旋，再左左单旋。图（2）为右左双旋，具体操作，先左左单旋，再右右单旋。

（4）C++代码

#ifndef AVLSEARCHTREE_H
#define AVLSEARCHTREE_H


#include


using namespace std;


template
struct TreeNode
{
T element;
int height; //此节点为根的子树的高度
int frequent; //频率
TreeNode* left;
TreeNode* right;
TreeNode()
{
left = NULL;
right = NULL;
frequent = 1;
height = 0;
}
};


template
class AVLSearchTree
{


public:
AVLSearchTree()
{
m_root = NULL;
}
void insert(T t)
{
insert(m_root, t);
}
TreeNode* find(T t)
{
return find(m_root, t);
}
void deleteNode(T t)
{
deleteNode(m_root, t);
}
void printInMidOrder()
{
printInMidOrder(m_root);
}
private:
void insert(TreeNode*& node, T t)


{
if (node == NULL)
{
node = new TreeNode();
node->element = t;
return;
}


if (node->element > t)
{
//大于t,则树的左边插入
insert(node->left, t);
if (2 == (height(node->left)-height(node->right)))
{
if (t < node->left->element)
{
SingRotateLeft(node);
}
else
{
DoubleRotateLR(node);
}//t < node->left-element
}//2==
}
else if (node->element < t)
{//
insert(node->right, t);
if (t == 3)
{
int i = 0;
}
if (2 == height(node->right) - height(node->left))
{
if (t > node->right->element)
{
SingRotateRight(node);
}
else 
{
DoubleRotateRL(node);
}
}
}//node->element < t
else 
{
node->frequent++;
}

//更新节点的高度信息
node->height = Max(height(node->left), height(node->right)) + 1;
}


TreeNode* find(TreeNode* node, T t)
{
if (node == NULL)
{
return NULL;
}


if (node->element > t)
{
return find(node->right, t);
}
else if (node->element < t)
{
return find(node->left, t);
}
else
{
return node;
}
}


void deleteNode(TreeNode* node, T t)
{
if (node == NULL)
{
return;
}


if (t < node->element)
{
deleteNode(node->left,  t);
if (2 == height(node->right) - height(node->left))
{
if (node->right->left != NULL && (height(node->right->left) > height(node->right->right)))
{
DoubleRotateRL(node);
}
else
{
SingRotateRight(node);
}
}
}// t < node.element
else if (t > node->element)
{
deleteNode(node->right, t);
if (node->left->right != NULL && (height(node->left->right) > height(node->left->left)))
{
DoubleRotateLR(node);
}
else
{
SingRotateLeft(node);
}
}
else 
{
//节点相等
if (node->left != NULL && node->right != NULL)
{
//有两个子节点
TreeNode* tmp = node->right;
while (tmp->left != NULL)
{
tmp = tmp->left;
}


node->element = tmp->element;
node->frequent = tmp->frequent;
deleteNode(node->right, tmp->element);


if (2 == height(node->left)-height(node->right))
{
if (node->left->right != NULL && (height(node->left->right)>height(node->left->left)))
{
DoubleRotateLR(node);
}
else
{
SingRotateLeft(node);
}
}
}//有1个或者0个节点
else
{
TreeNode* tmp = node;
if (node->left == NULL)
{
node = node->right;
}
else if (node->right == NULL)
{
node = node->left;
}


delete tmp;
tmp = NULL;
}
}//值相等


if (node == NULL)
{
return;
}


node->height = Max(height(node->left), height(node->right))+1;
return;
}


void printInMidOrder(TreeNode* node)
{
if (node == NULL)
{
return;
}


printInMidOrder(node->left);
cout << node->element << " ";
printInMidOrder(node->right);
}



//获取该节点的高度
//计算该节点的深度
int height(TreeNode* node)
{
if (node != NULL)
{
return node->height;
}


return -1;
}

//左左旋转
void SingRotateLeft(TreeNode*& k2)
{
TreeNode* k1;
k1 = k2->left;
k2->left = k1->right;
k1->right = k2;


k2->height = Max(height(k2->left), height(k2->right)) + 1;
k1->height = Max(height(k1->left), k2->height) + 1;

k2 = k1;
}

//右右情况下的旋转
void SingRotateRight(TreeNode*& k2)
{
TreeNode* k1;
k1 = k2->right;
k2->right = k1->left;
k1->left = k2;

//如果交换k2和k1，如何将新的k1点与k2建立联系
//按目前这种方法，比如会将k2节点全部下面的值全部都丢掉
//k2 = k1;


k2->height = Max(height(k2->left), height(k2->right)) + 1;
k1->height = Max(height(k1->right), k2->height) + 1;


k2 = k1;
}

//左右旋转
void DoubleRotateLR(TreeNode*& k3)
{
SingRotateRight(k3->left);
SingRotateLeft(k3);
}

//右左旋转
void DoubleRotateRL(TreeNode*& k3)
{
SingRotateLeft(k3->right);
SingRotateRight(k3);
}


int Max(int a, int b)
{
return a>=b? a: b;
}


private:
TreeNode* m_root;
};




#endif