【数据结构与算法】二叉树的链式访问
作者：一只大喵咪1201
专栏：《数据结构与算法》
格言：你只管努力，剩下的交给时间！
二叉树
- 链式存储
-
- 创建二叉树
- 二叉树的常用操作
-
- 二叉树的遍历访问
- 二叉树的层序访问
- 二叉树节点个数
- 二叉树叶子节点个数
- 二叉树第k层节点个数
- 二叉树的高度
- 二叉树查找值为x的节点
- 二叉树的创建和销毁
-
- 二叉树的创建
- 二叉树销毁
- 总结
链式存储
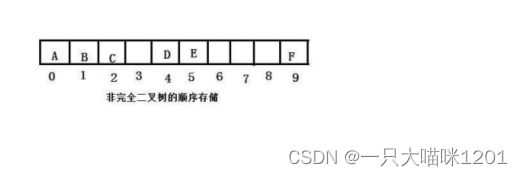
在前面我本喵曾讲解过二叉树中的堆在内存中是顺序存储的，在逻辑上是一个完全二叉树，那么如果有一颗非完全二叉树怎么储存呢？
来看看仍然按照顺序储存的方式，首先我们得将它补成一个完全二叉树
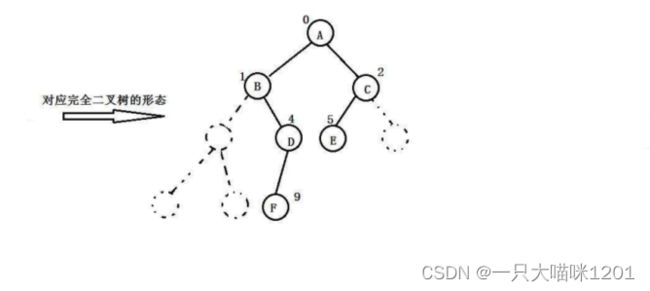
然后再按照父子对应关系顺序储存在内存中
非完全二叉树在内存中顺序储存时：
- 造成内存空间浪费
可以看到，将非完全二叉树按照顺序储存是不合适的，所以我们采用另一种方式，以链表的方式储存非完全二叉树。
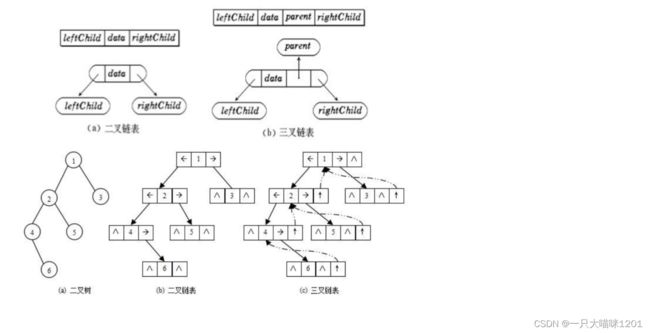
链式存储：
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链，当前本喵学习的一般都是二叉链，后面学到高阶数据结构如红黑树等会用到三叉链。
链式储存的优势：
- 不会造成空间浪费，内存空间按需开辟
现在已经清楚了二叉树的链式储存，接下来本喵带着大家看看如何使用。
创建二叉树
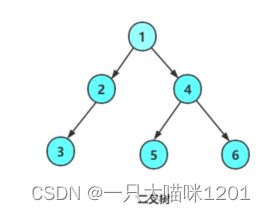
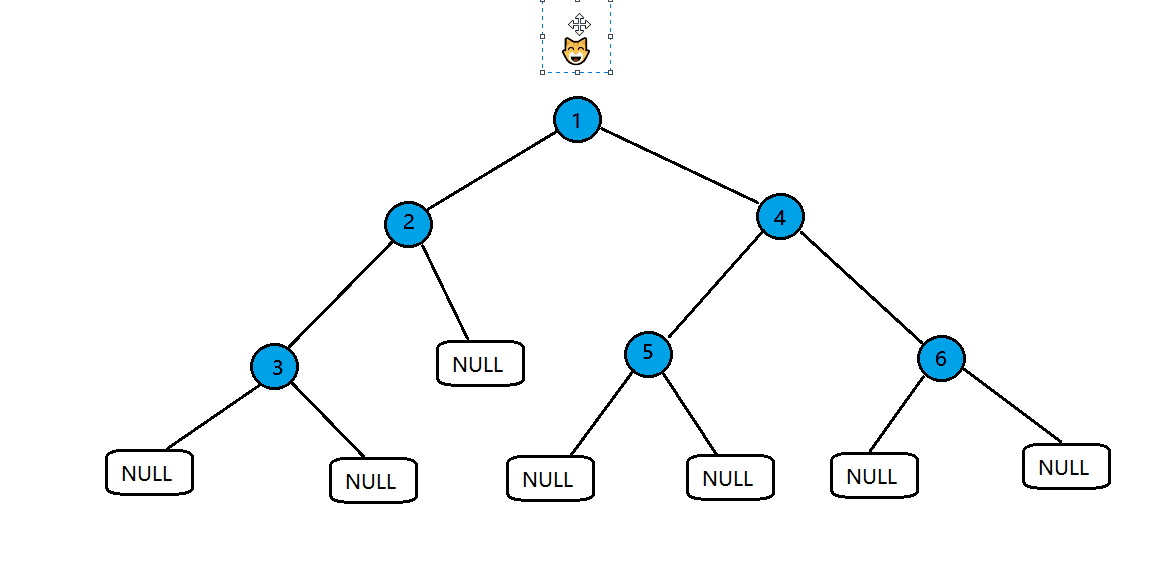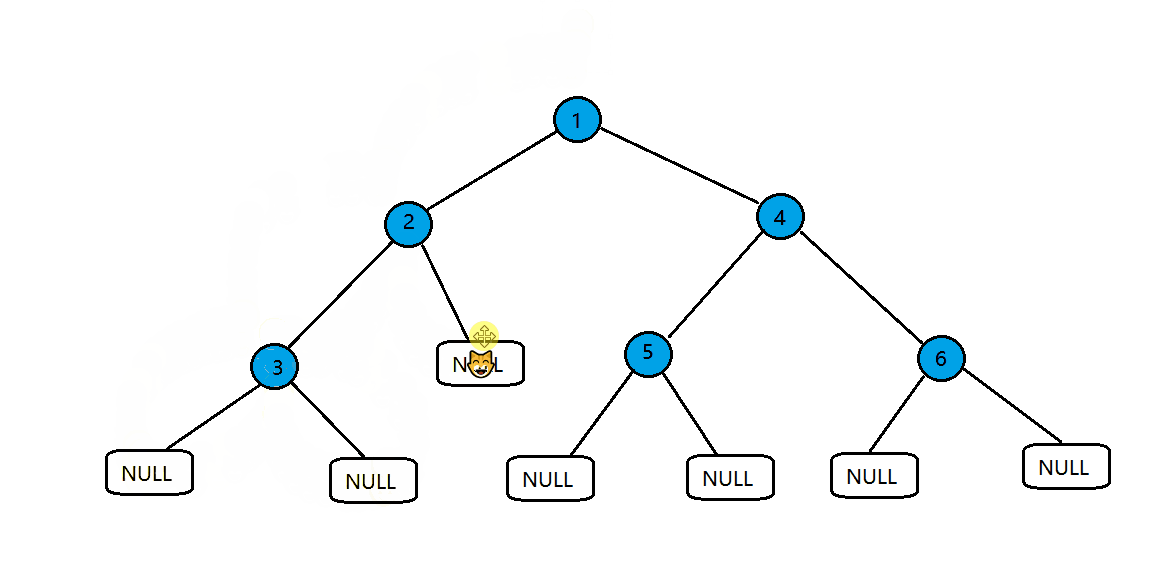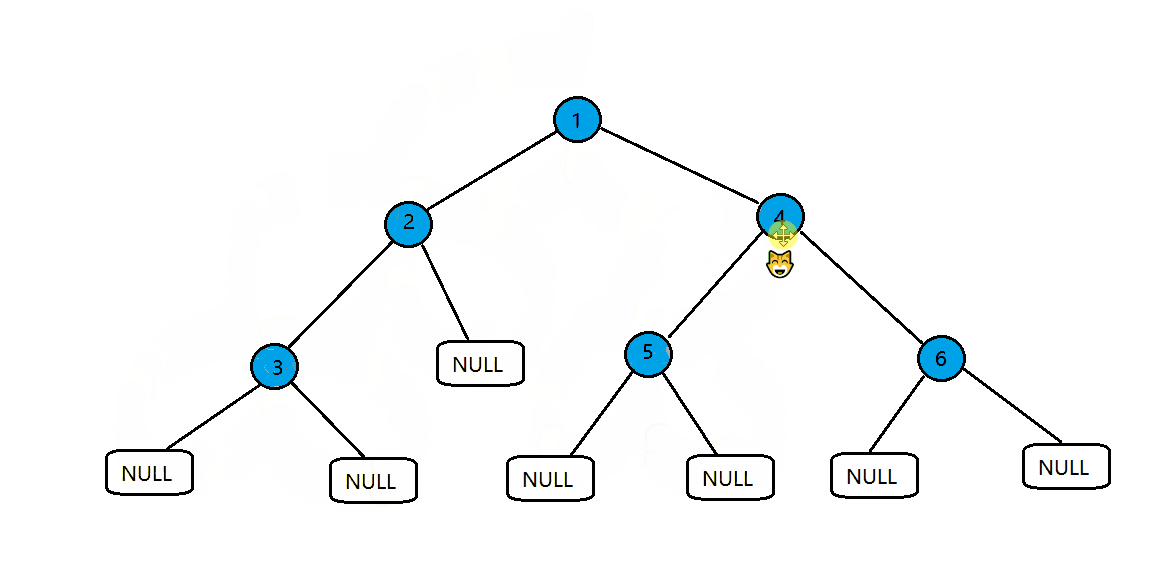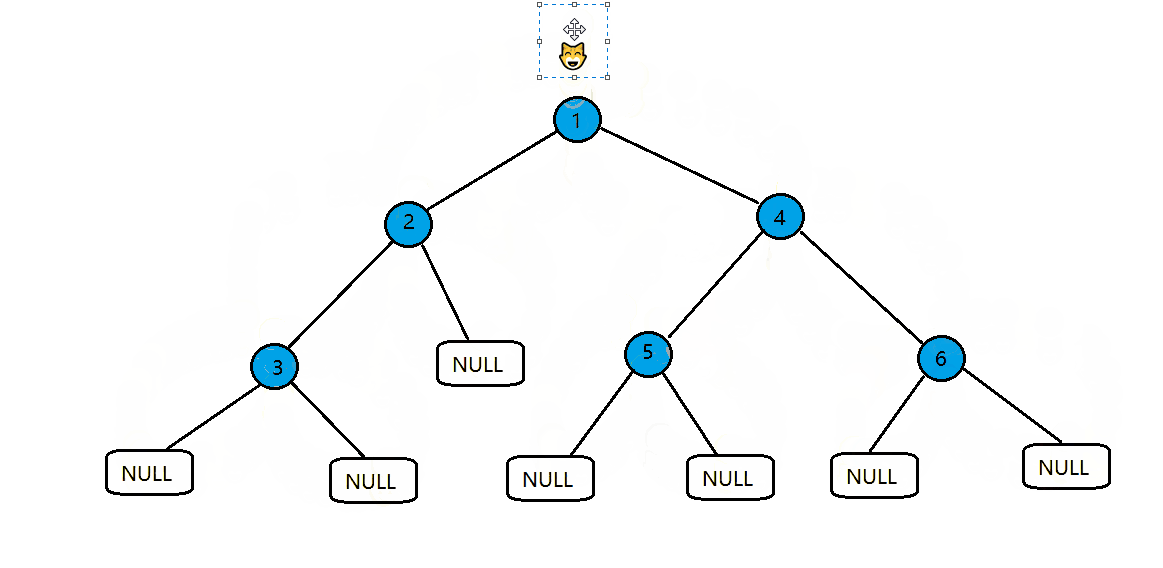
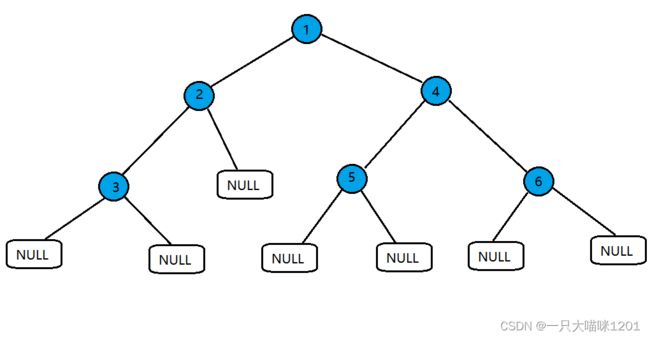
我们在接下来需要用到二叉树这个数据结构，在这里先创建一个二叉树
按照上图中的二叉树创建
typedef int BTDataType;//二叉树节点中的数据类型
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//创建二叉树
BTNode* CreateTree()
{
BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));//开辟节点空间
assert(n1);//有效性检验
BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));//开辟节点空间
assert(n2);//有效性检验
BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));//开辟节点空间
assert(n3);//有效性检验
BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));//开辟节点空间
assert(n4);//有效性检验
BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));//开辟节点空间
assert(n5);//有效性检验
BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));//开辟节点空间
assert(n6);//有效性检验
//节点赋值
n1->data = 1;
n2->data = 2;
n3->data = 3;
n4->data = 4;
n5->data = 5;
n6->data = 6;
//节点指向
n1->left = n2;
n1->right = n4;
n2->left = n3;
n2->right = NULL;
n3->left = NULL;
n3->right = NULL;
n4->left = n5;
n4->right = n6;
n5->left = NULL;
n5->right = NULL;
n6->left = NULL;
n6->right = NULL;
//返回根
return n1;
}
一个二叉树到此就建好了。
注意： 上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重讲解。
二叉树的常用操作
二叉树中有许多的操作，下面本喵给大家介绍一些常用的操作。
二叉树的遍历访问
学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal) 是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根，所以N(Node）、 L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。 NLR、 LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
- 前序遍历
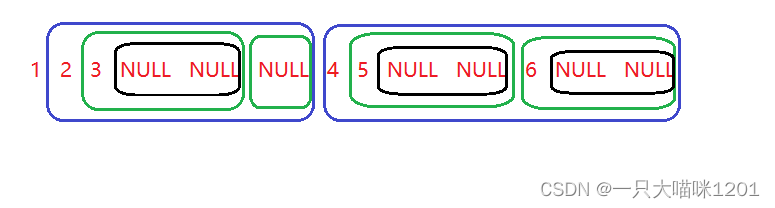
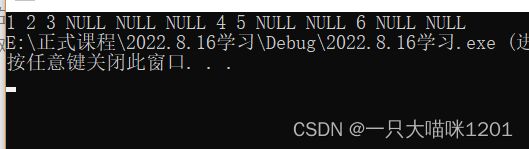
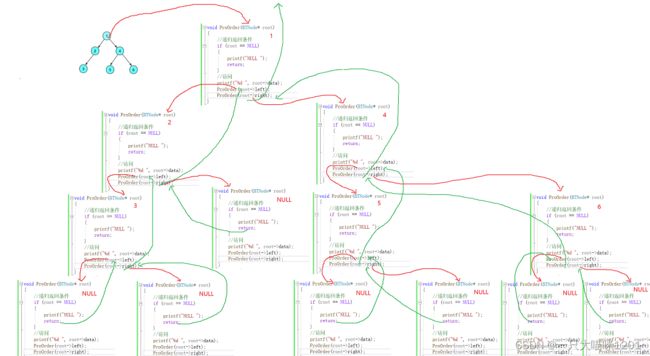
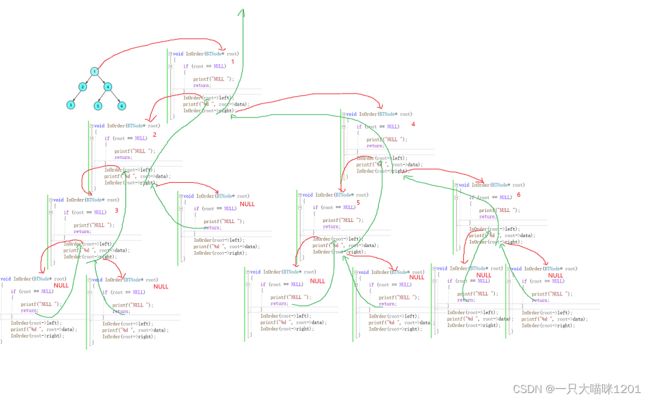
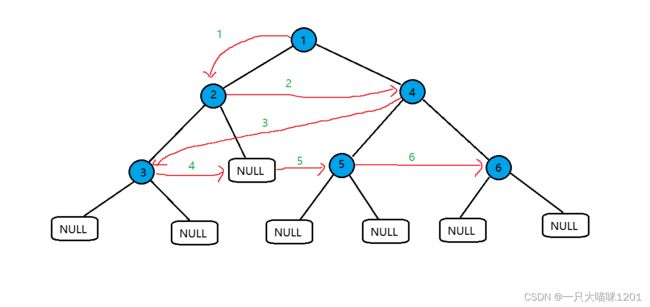
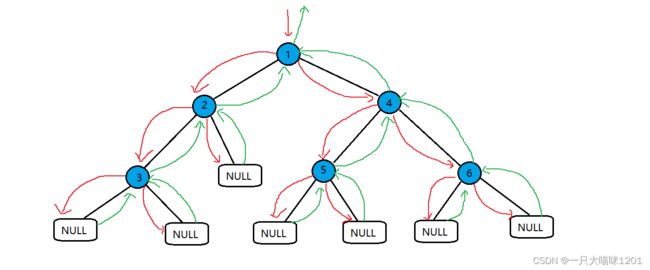
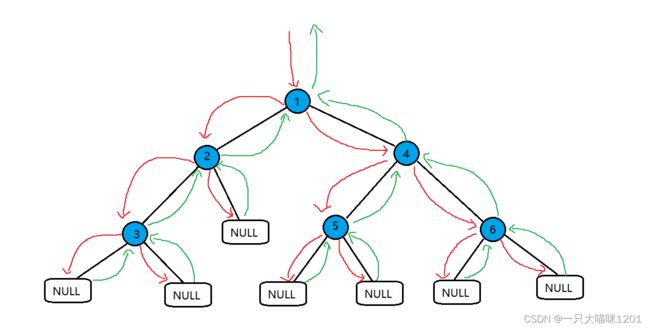
将我们创建的二叉树进行前序遍历，按照根->左子树->右子树的顺序来访问。
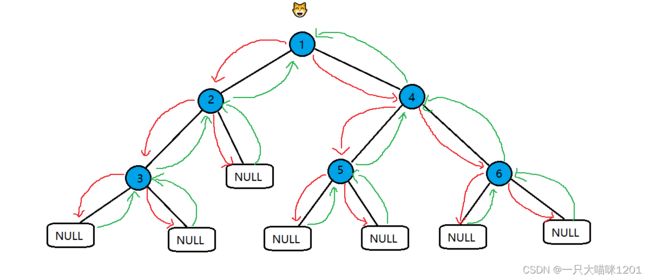
这里增加了每个节点指向的空，图中猫咪走过的路径就是它的访问路径。
进行访问时猫咪就会进入圆圈或者框中，不访问只是返回猫咪就不会进去。
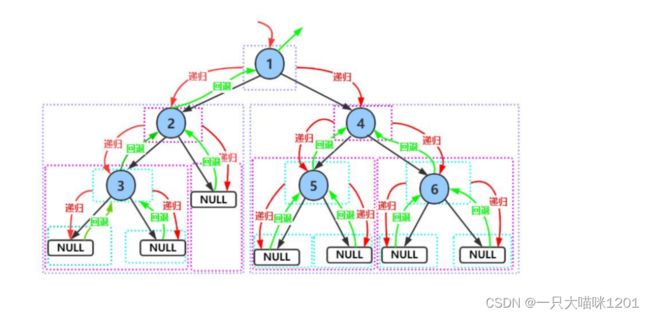
这是它的静态图其中红色箭头表示递归的过程，绿色箭头表示回退的过程。
按顺序访问的结果：
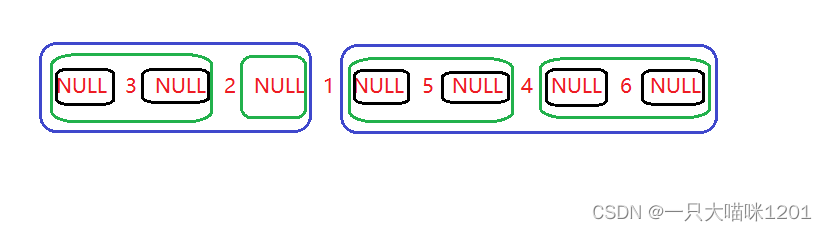
- 1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
这个图是非常有讲究的。
- 俩个蓝色框是1的左右子树
- 蓝色框中的俩个绿色框分别是子树的左右子树
- 绿色框中的黑色框是子树的子树的左右子树
- 它们都是相同的结构，根——左子树——右子树
去掉NULL后按顺序访问的结果
- 1 2 3 4 5 6
访问流程我们已经清楚了，接下看代码如何实现：
void ProOrder(BTNode* root)
{
//递归返回条件
if (root == NULL)
{
printf("NULL ");
return;
}
//访问
printf("%d ", root->data);
ProOrder(root->left);
ProOrder(root->right);
}
和我们分析的结果一致。
是不是发现代码好简单？确实非常的简单，但是这个递归的过程可不简单，下面本喵画一个函数栈帧的调用过程图给大家分析一下递归的过程。
其中红线是调用过程，绿线回退过程。
- 中序遍历
将我们创建的二叉树进行前序遍历，按照左子树——根——右子树的顺序访问。
图中猫咪走过的路径就是它的访问路径。
进行访问时猫咪就会进入圆圈或者框中，不访问只是返回猫咪就不会进去。
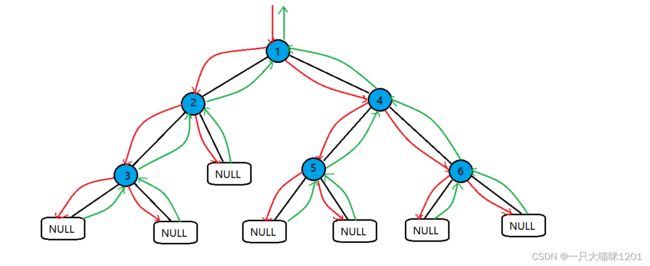
这是它的静态图其中红色箭头表示递归的过程，绿色箭头表示回退的过程。
按顺序访问的结果：
- NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
它的结果同样是非常有讲究的。
- 俩个蓝色框是1的左右子树
- 蓝色框中的俩个绿色框分别是子树的左右子树
- 绿色框中的黑色框是子树的子树的左右子树
- 它们都是相同的结构，左子树——根——右子树
去掉NULL后按顺序访问的结果
- 3 2 1 5 4 6
访问流程我们已经清楚了，接下看代码如何实现：
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
和我们分析的结果一致。
同样本喵在画一次函数栈帧调用图
其中红线是调用过程，绿线回退过程。
- 后序遍历
将我们创建的二叉树进行前序遍历，按照左子树——右子树——根的顺序访问。
图中猫咪走过的路径就是它的访问路径。
进行访问时猫咪就会进入圆圈或者框中，不访问只是返回猫咪就不会进去
静态图和前面是一样的，看不出什么。
按顺序访问的结果：
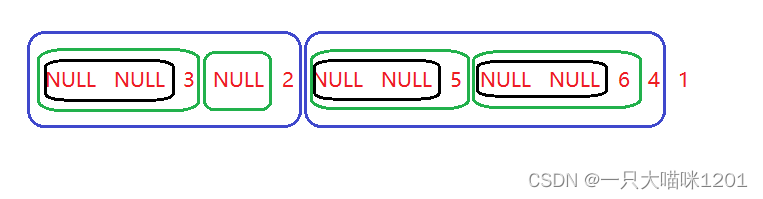
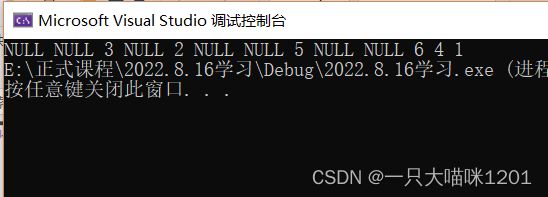
- NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
它的结果同样是非常有讲究的。
- 俩个蓝色框是1的左右子树
- 蓝色框中的俩个绿色框分别是子树的左右子树
- 绿色框中的黑色框是子树的子树的左右子树
- 它们都是相同的结构，左子树——右子树——根
去掉NULL后按顺序访问的结果
- 3 2 5 6 4 1
访问流程我们已经清楚了，接下看代码如何实现：
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
和我们分析的结果一致。
相信大家已经学会如何画函数栈帧调用图了，这里本喵就不画了。
二叉树的层序访问
层序遍历不是采用的链式访问，也就是说它不是通过递归实现的，而是通过迭代实现的。
按照上面的顺序一层一层的访问。
那么具体是通过什么样的方式呢？
这里我们借助链表来实现。
来看动图，将上面的链表进行遍历
过程：
- 根节点入队列，再将队首元素出队列打印，同时将该节点的左右子节点入队列
- 再次将队首元素出队列打印，同时将该节点的左右子节点入队列
- 如此重复，当节点数据是NULL时不进队列，直到所有的值都出了队列，此时访问完毕。
看动图中，可以看到，后面入队列的子节点全部都排再后面，出队首元素并不影响它们，这里充分利用了队列的特性。
代码实现：
这里使用到的队列是在前面实现的，本喵的的文章栈和队列中有详细讲解。这里我们直接使用。
void LevelOrder(BTNode* root)
{
assert(root);
Queue q;
QueueInit(&q);//队列初始化
//根节点入队列
if (root)
QueuePush(&q, root);
//重复操作
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);//暂时记录队首元素
QueuePop(&q);//出队列
printf("%d ", Front->data);//打印
//如果不是NULL则左边子节点入队列
if (Front->left)
QueuePush(&q, Front->left);
//如果不是NULL则右边子节点入队列
if (Front->right)
QueuePush(&q, Front->right);
}
printf("\n");
QueueDestroy(&q);
}
层序遍历的结果很明显就是这个。
二叉树节点个数
同样使用的是我们上面创建好的二叉树。
同样采用的是链式访问，也就是使用递归来实现。
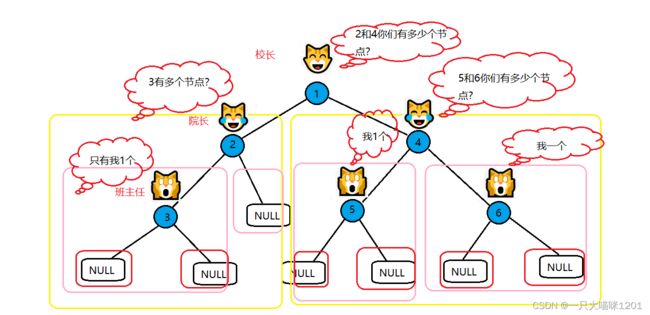
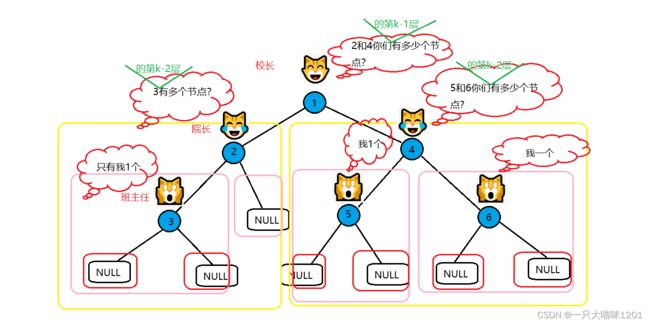
实现的思想是分治的思想：
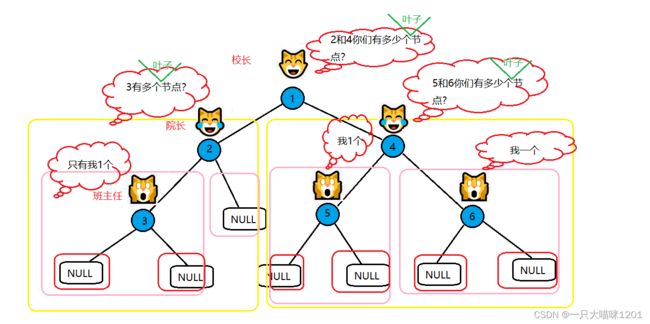
- 校长猫统计俩只院长猫报上来的节点个数，然后上报学校
- 俩只院长猫都统计班主任猫报上来的节点数，然后上报给校长
- 班主任猫统计各自班中的节点个数，然后上报给院长
这样一来，所有节点个数就 统计出来了。
按照这种思想，我们来看一下具体的访问流程
这个流程和我前面的遍历流程很相似。
来看代码的实现：
//求二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return (1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right));
}
- 返回中的1是每个子树的根节点，也就是自身
- 当递归到NULL的时候，返回的个是0
结果和我们数出来是一样的，是6个。
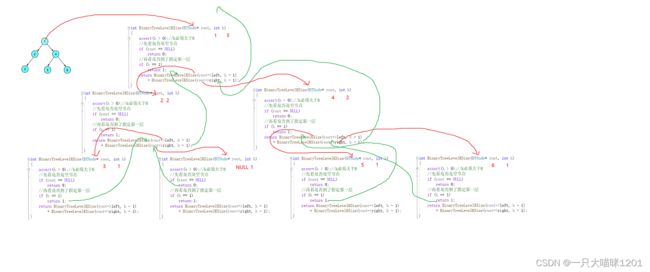
再来看一下它的函数栈帧调用图
其中红线是调用过程，绿线回退过程。
二叉树叶子节点个数
同样使用的是我们上面创建好的二叉树。
同样使用的分治思维
和上面求节点个数一样，
- 校长猫统计俩只院长猫报上来的叶子节点个数，然后上报学校
- 俩只院长猫都统计班主任猫报上来的叶子节点数，然后上报给校长
- 班主任猫统计各自班中的叶子节点个数，然后上报给院长
只是这里不一样的是，需要设置一些条件来判断是不是叶子节点。
条件：
- 左子树和右子树都是空的时候，该节点就是叶子节点。
访问流程还是一样
红线是递归，绿线是回退。
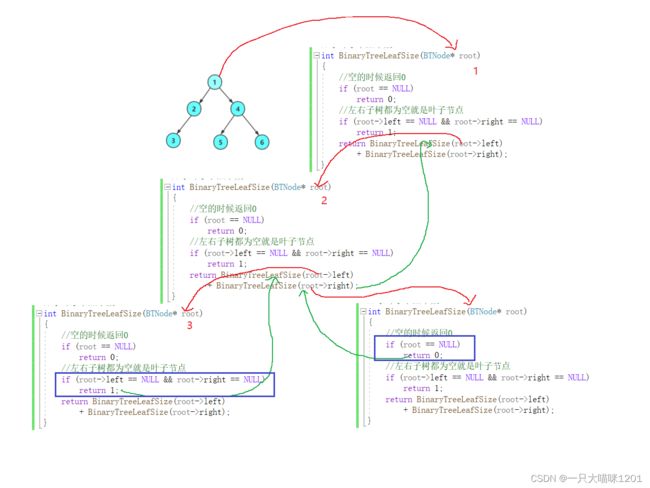
其实这个流程图光看线是没有用的，它的访问顺序都是这样的，重要的是在走流程图的时候要构思好代码思路。
来看代码的实现：
//求叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
//空的时候返回0
if (root == NULL)
return 0;
//左右子树都为空就是叶子节点
if (root->left == NULL && root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left)
+ BinaryTreeLeafSize(root->right);
}
从图中看确实是有3个叶子节点。
注意
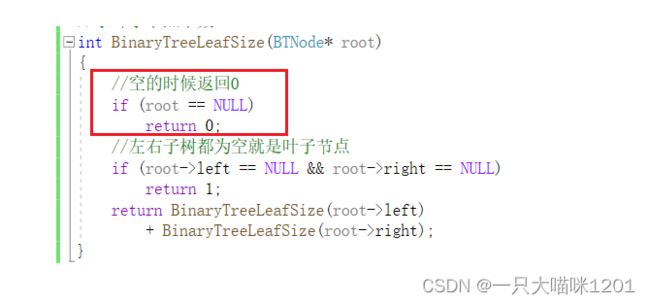
红色框中的返回条件必须有，否则在只有一个子树的节点处会出问题。
这里俩个返回条件都会用得到，缺一个都不行。
二叉树第k层节点个数
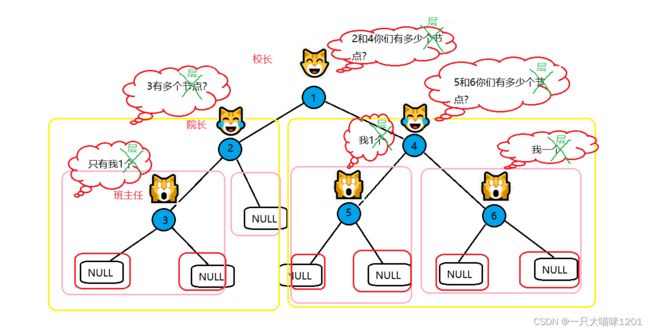
同样使用分治思想
- 校长猫统计俩只院长猫报上来的k-1层叶子节点个数，然后上报学校
- 俩只院长猫都统计班主任猫报上来的k-2层叶子节点数，然后上报给校长
- 班主任猫统计各自班中的k-3层叶子节点个数，然后上报给院长
访问流程本喵就不画了，和前面的是一样的。
限制条件
- 当节点为空的时候返回0
- 当k为1的时候返回1
来看代码的实现：
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);//k必须大于0
//先看是否是空节点
if (root == NULL)
return 0;
//再看是否到了指定那一层
if (k == 1)
return 1;
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
可以看到，第三层的节点个数就是3。
函数栈帧调用图
- 先判断该节点是否为空
- 如果不是空再看k是否为1
二叉树的高度
同样使用分治思想
- 校长猫统计俩只院长猫报上来的较大层数，然后上报学校
- 俩只院长猫都统计班主任猫报上来的较大层数，然后上报给校长
- 班主任猫统计各自班中的较大层数，然后上报给院长
访问流程图，还是和前面的一样：
返回值
- 每次返回的值都是左右子树中较大的那一个
代码实现：
int BinaryTreeHight(BTNode* root)
{
if (root == NULL)
return 0;
//求左子树高度
int lefthight = BinaryTreeHight(root->left);
//求右子树高度
int righthight = BinaryTreeHight(root->right);
//返回较大值
return lefthight > righthight ? lefthight + 1 : righthight + 1;
}
可以看到，我们创建的树的高度是3。
函数栈帧调用图：
这里本喵仅画了一半的图，剩下的一半有兴趣的话可以自己画一下。
二叉树查找值为x的节点
这里采用的遍历查找的思维，采用前序遍历，只是将打印部分换成比较。
限制条件：
- 节点为空返回空
- 节点的值与要找的值相等，返回该地址
代码实现：
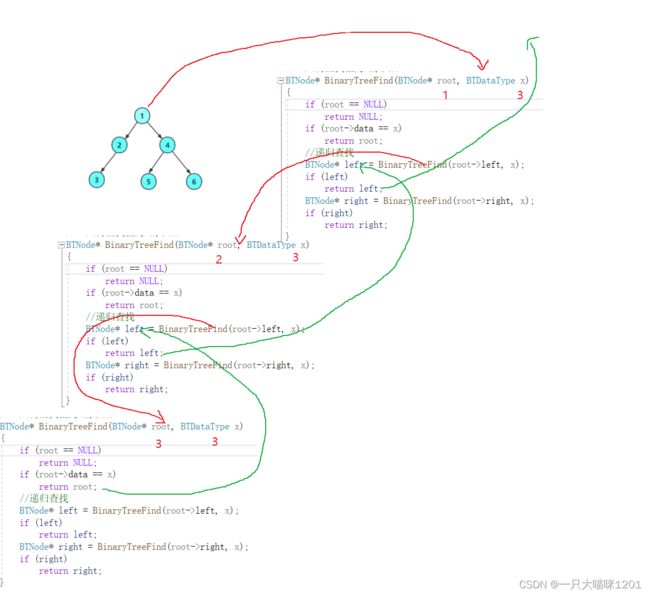
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
//递归查找
BTNode* left = BinaryTreeFind(root->left, x);
if (left)
return left;
BTNode* right = BinaryTreeFind(root->right, x);
if (right)
return right;
return NULL;
}
根据调试我们可以看到确实找到了。
函数栈帧调用图
本喵画的是找x为3的栈帧调用图
- 函数最后需要返回值的，要即时return，不让递归进行下去。
二叉树的创建和销毁
二叉树的创建
这里的二叉树创建才是真正的创建。
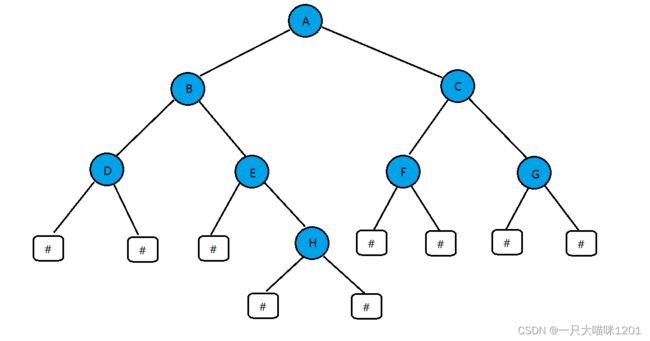
这里有一个字符串"ABD##E#H##CF##G##"，其中‘#’空格，将这个字符串按照前序遍历的方式储存到二叉树中。
假设上面字符串是前序遍历一个二叉树的结果，遇到#返回，那么我就可以按照前序遍历的顺序来推出二叉树的样子。
- A是根节点，B是A左子树的根节点，D是B左子树的根节点，俩个#是D的左右子树
- E是B的右子树，#是E的左子树，H是E的右子树，俩个#是H的左右子树
- C是A的右子树，F是C的左子树，俩个#是F的左右子树
- G是C的右子树，俩个#是G的左右子树
画成二叉树就是
接下来要做的就是将字符串按照这个样子存储。
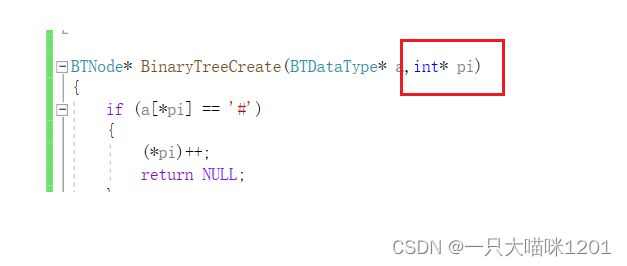
BTNode* BinaryTreeCreate(BTDataType* a,int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
root->data = a[*pi];
(*pi)++;
root->left = BinaryTreeCreate(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}
这里采用的逻辑就是前序遍历的逻辑，只是有些地方不一样而已。
主函数中代码很简单，本喵就不展示了。
注意：
红色框中的形成必须是一级指针，它是用来控制数组a的下标的。
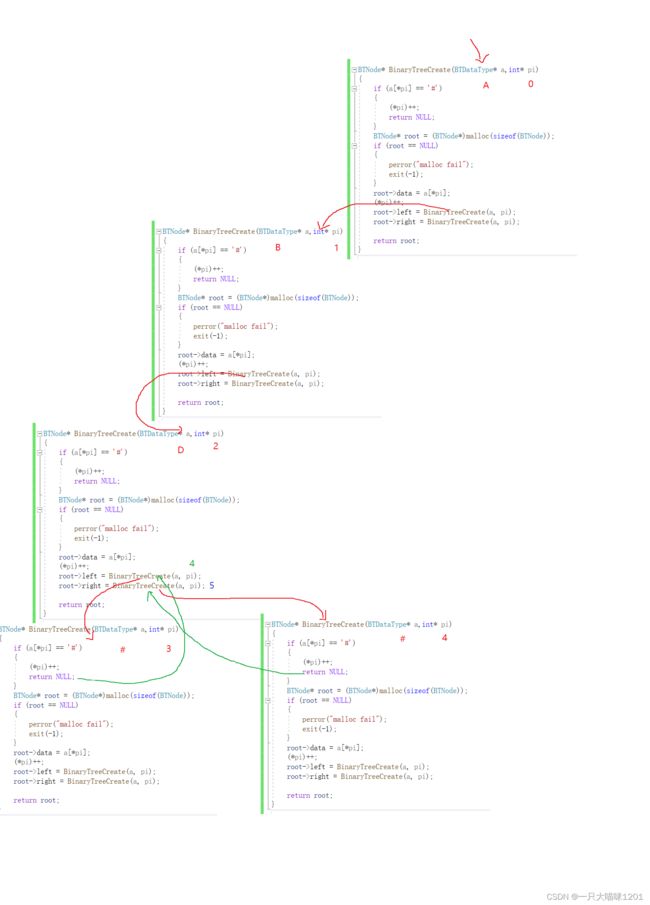
如果不用指针的画，最后一层调用中i是3，左子树返回以后i就成了2，左子树中i++的结果在函数调用结束后就不存在了，所以调用右子树的时候，i的值仍然是3，就达不到指向下一个字符的效果。
红色框部分，在函数调用结束以后有了返回值才链接在二叉树上。
二叉树销毁
这个比较简单，但是释放时要注意顺序。
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
return ;
BinaryTreeDestroy(root->left);
BinaryTreeDestroy(root->right);
free(root);
}
这里必须先释放左右子树，然后才能释放根，采用的逻辑是后续遍历的逻辑。
总结
以上便是二叉树链式访问的一些基本操作，值得注意的是，递归流程图以及函数栈帧的调用图相差都不是很多，它们的作用就是在画图的时候可以规划好写代码的思路，虽然图一样，但是代码可不一样。
希望对大家有所帮助。