【LeetCode 简单题】28-杨辉三角II
声明:
今天是第28道题。给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。以下所有代码经过楼主验证都能在LeetCode上执行成功,代码也是借鉴别人的,在文末会附上参考的博客链接,如果侵犯了博主的相关权益,请联系我删除
(手动比心ღ( ´・ᴗ・` ))
正文
题目:给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。在杨辉三角中,每个数是它左上方和右上方的数的和。
![]()
示例:
输入: 3 输出: [1,3,3,1]
解法1。前k行的序列可以用上一篇博客(见27-杨辉三角)的思路完成,然后直接返回第k个元素,代码如下
class Solution:
def getRow(self, rowIndex):
pt = [[1]]
for i in range(rowIndex):
pt.append(list(map(lambda x,y:x+y, [0]+pt[-1],pt[-1]+[0])))
return pt[rowIndex]解法2。O(k)的做法
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
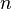 行的数字个数为
行的数字个数为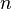 个。
个。 - 第
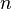 行的第
行的第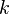 个数字为组合数。
个数字为组合数。 - 第
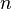 行数字和为。
行数字和为。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
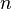 行第
行第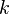 个数字等于第
个数字等于第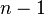 行的第个数字与第
行的第个数字与第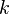 个数字的和)。这是因为有组合恒等式:。可用此性质写出整个杨辉三角形。
个数字的和)。这是因为有组合恒等式:。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用O(k)的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法, 我最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码参见评论区一楼。本地调试输出前十行,没啥问题,拿到OJ上测试,程序在第18行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整形数int的数值范围只有-32768到32768之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的OJ肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个for循环,除了第一个数为1之外,后面的数都是上一次循环的数值加
class Solution(object):
def getRow(self, rowIndex):
"""
:type rowIndex: int
:rtype: List[int]
"""
if rowIndex <= 0:
return [1]
res = [0]*(rowIndex+1)
res[0] = 1
for i in range(1, rowIndex+1):
for j in range(i, 0, -1):
res[j] += res[j-1]
return res结尾
解法1:https://blog.csdn.net/weixin_41011942/article/details/82810881