哈希(解决哈希冲突,封装map/set,哈希的应用{位图/布隆过滤器})
文章目录
- 如何解决哈希冲突:
-
- ①闭散列:也叫开放定址法,如果发送哈希冲突了,就去找下一个空位置
- ②开散列 -- 拉链法/哈希桶
- 封装map和set
-
- 哈希表的代码
- 封装的unordered_set
- 封装的unordered_map
- 哈希的应用
-
- 位图
-
- 实现位图:
- 布隆过滤器
-
- 实现布隆过滤器
- 布隆过滤器扩展
一.哈希(按某种规律将某个值存储到固定位置)
除留余数法 key % len
直接映射一定是有哈希碰撞/哈希冲突
如何解决哈希冲突:
①闭散列:也叫开放定址法,如果发送哈希冲突了,就去找下一个空位置
针对的是值相对连续的做法,如果说值特别的散,那么效率会很低
方法一:线性探测,从发送冲突的位置开始,依次向后探测,直到找到下一个空位置为止
(图书馆抢位置,别人如果枪了我的,我就去抢别人的,强盗逻辑)
构建哈希表:
一个vector,一个记录有效个数的变量n
如果vector的最后一个数据冲突则返回到vector的第一个位置继续找空位
删除元素后查找遇到空时回暂停,如何解决这种问题呢?加标记,每个数据给一个枚举状态值,这样删数据只需要将其状态值修改
查找时遇到空EMPTY就停止了,遇到删除DELETE还要继续找
负载因子定义 α = 填入表中的元素个数 / 散列表的长度
α越大,冲突的概率越大,效率低,但是浪费少
α越小,冲突的概率越小,效率高,但是浪费严重
接口:
【 插入 】算插入位置,膜vector的size而不是capacity ,扩容的写法(α>0.7)
扩容时:直接new一个新的table,将原table中元素插入其中,交换指针即可,复用之前insert
重复插入的处理(通过Find接口)
插入的数据不一定是整数,可能是string…用仿函数的方式来解决,取模的地方就用仿函数处理一下
各种字符串Hash函数-博客园
注意:
vector的reserve以后为什么不能cin>>v[i],因为方括号自带检查,reserve只是开空间并未初始化,所以要用resize(默认初始化为0)
方法二:二次探测
引入二次探测背景:连续位置的冲突值比较多的话,引发踩踏洪水效应,按照方法一找邻居的话比较容易冲突
#pragma once
#include②开散列 – 拉链法/哈希桶
是闭散列/开放定址法的优化:闭散列不同位置冲突数据会互相影响,相互位置的冲突会争抢位置,互相影响效率
开散列相邻位置冲突,不会再争抢位置,不会互相影响
控制负载因子 – 负载因子到了就扩容
极端场景防止一个桶冲突太多,链表太长:当一个桶长度超过一定长以后,转换为红黑树(Java中链表的长度超过了8会变成红黑树)
例子:
表长度100
极端场景:
1 .存了50个值,40个值是冲突的,挂再一个桶中
2 .存储了10000个值,平均每个桶长度100,阶段场景有些桶可能有上千个值
【插入】
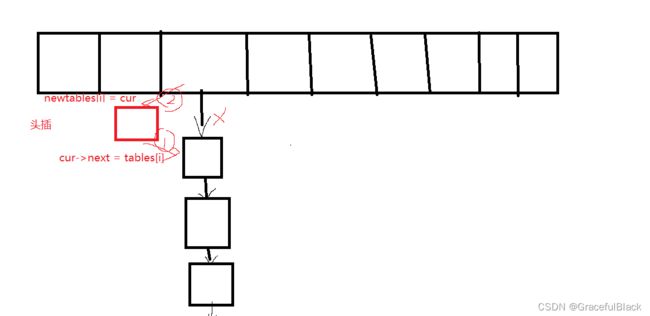
扩容:这种方法中的扩容最好不要复用自己的Insert,因为会new新的节点,这样是没有必要的,可以将原表中的节点一个个链下来,
注意是一个个,而不是一个桶(因为桶中的元素映射到了新表中可能对应新的位置)
table[i]的节点都被拿走了,最好要把它置空一下
newtable是我们的table想要的,把他们的指针再交换一下
namespace LinkHash
{
template<class K,class V>
struct HashNode
{
pair<K, V> _kv;
HashNode<K, V>* _next;
HashNode(const pair<K,V>& kv)
:_kv(kv),
_next(nullptr)
{}
};
template<class K,class V,class HashFunc = Hash<K>>
class HashTable
{
typedef HashNode<K, V> Node;
public:
bool Erase(const K& key)
{
//表空就不用删除
if (_tables.empty())
{
return false;
}
HashFunc hf;
size_t index = hf(key) % _tables.size();
Node* prev = nullptr;
Node* cur = _tables[index];
while (cur)
{
if (cur->_kv.first == key)
{
if (prev == nullptr)
{
//头删
_tables[index] = cur->_next;
}
else
{
//中间删除
prev->_next = cur->_next;
}
--_n;
delete cur;
return true;
}
else
{
prev = cur;
cur = cur->_next;
}
}
return false;
}
Node* Find(const K& key)
{
//表为空直接返回false
if (_tables.empty())
{
return nullptr;
}
HashFunc hf;
size_t index = hf(key) % _tables.size();
//给一个当前位置的指针,进行遍历查找
Node* cur = _tables[index];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
else
{
cur = cur->_next;
}
}
//没找到
return nullptr;
}
bool Insert(const pair<K, V>& kv)
{
//避免插入相同元素
Node* ret = Find(kv.first);
if (ret)
return false;
HashFunc hf;
//负载因子等于1的时候扩容
if (_n == _tables.size())
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*> newTables;
newTables.resize(newSize);
//将旧表中的节点转移到新表
//一个一个Node插入新表因为将一个桶直接链过去桶内的元素在新表的映射关系可能会发生改变
for (size_t i = 0;i<_tables.size();i++)
{
//_tables[i]实际上存的就是每个节点的指针
Node* cur = _tables[i];
//如果当前节点不是空
while (cur)
{
Node* next = cur->_next;
size_t index = hf(cur->_kv.first) % newTables.size();
//头插
cur->_next = newTables[index];
newTables[index] = cur;
cur = next;
}
//旧表的所有元素进入新表后,将旧表的节点清空
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
//计算位置并插入新节点
size_t index = hf(kv.first) % _tables.size();
Node* newNode = new Node(kv);
newNode->_next = _tables[index];
_tables[index] = newNode;
++_n;
return true;
}
private:
//实际上是个指针数组
vector<Node*> _tables;
size_t _n = 0;
};
void TestHashTable()
{
int a[] = { 4, 24, 14,7,37,27,57,67,34,14,54 };
HashTable<int, int> ht;
for (auto e : a)
{
ht.Insert(make_pair(e, e));
}
ht.Insert(make_pair(84, 84));
}
}
封装map和set
面试题:
一个类型要去做map和set的key有什么要求;做unordered_map和unordered_set的key又有什么要求?
map的key :Key类型对象支持小于比较或者传递一个小于仿函数即可
unordered_map的key:a .能支持取模或者支持转换成取模的无符号整数 b .支持key比较相等或者相等的仿函数
什么时候需要自己写仿函数
1.类型不支持比较大小
2.支持比较大小,但是不是你想要的
unordered_map什么时候需要自己实现仿函数
1 .想要的类型不支持相等(equal)的比较
2 .自定义类型不满足自己需求的类型(举例 Date和Date*)
map是如何只支持小于比较,从而完成大于和相等
map只要求key能够比较大小,比它小往左边走,比它大往右边走,不大不小就是相等
map只需要实现一个小于即可,大于(仿函数换一下位置即可)
多一层keyofT封装,通过key找value
统一适配
这样set找的就是它的K,map的话找的是它pair中的first
哈希表支持迭代器
互相引用的问题(迭代器引用哈希表,哈希表引用迭代器),需要加一个前置申明,说明是一个类模板
私有的问题,用到哈希表中的tables 加一个有元
迭代器不需要实现–,–需要用到双向链表
map的方括号
在的值可以返回对应的value,可以充当查找的功能
直接写的话是插入+修改
重写拷贝构造
生成默认构造的前提是没有其他构造,我们在写拷贝构造后需要自己手动写默认构造
拷贝构造是一个特殊的默认构造函数
C++11语法显示地去生成默认构造 ()=default
哈希表的大小最好是素数比较好,通过查看源码我们知道,用了一个素数表
哈希表的代码
#pragma once
#include ht;
for (auto e : a)
{
ht.Insert(make_pair(e, e));
}
ht.Insert(make_pair(84, 84));*/
}
}
封装的unordered_set
#pragma once
#include"HashTable.h"
namespace zkx
{
template<class K,class hash = Hash<K>>
class unordered_set
{
struct SetKeyofT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
//typename创建后再初始化,先是一个申明
typedef typename LinkHash::HashTable<K, K, SetKeyofT, hash>::iterator iterator;
iterator begin()
{
return _ht.begin();
}
iterator end()
{
return _ht.end();
}
bool insert(const K& key)
{
return _ht.Insert(key);
}
private:
LinkHash::HashTable<K,K,SetKeyofT,hash> _ht;
};
void test_unordered_set()
{
unordered_set<int> us;
us.insert(1);
us.insert(2);
us.insert(3);
us.insert(4);
unordered_set<int>::iterator it = us.begin();
while (it != us.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
}
封装的unordered_map
#pragma once
#include"HashTable.h"
namespace zkx
{
template<class K,class V,class hash =Hash<V>>
class unordered_map
{
struct MapKeyofT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename LinkHash::HashTable<K, pair<K, V>, MapKeyofT, hash>::iterator iterator;
iterator begin()
{
return _ht.begin();
}
iterator end()
{
return _ht.end();
}
bool insert(const pair<K,V>& kv)
{
return _ht.Insert(kv);
}
bool erase(const pair<K, V>& kv)
{
return _ht.Erase(kv.first);
}
private:
LinkHash::HashTable<K, pair<K, V>, MapKeyofT, hash> _ht;
};
void test_unordered_map()
{
unordered_map<string, string> um;
um.insert(make_pair("string","字符串"));
um.insert(make_pair("umbrella", "雨伞"));
unordered_map<string, string>::iterator it = um.begin();
while (it != um.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
cout << endl;
}
}
哈希的应用
位图
1 .面试题:55:46
给40亿个无符号整数,没排过序。给一个无符号整数们如何快速判断一个数是否在这40亿个数中【腾讯】
如果是排好序的,2^30 = 10亿左右,那么最多只要查找32次
40亿个整数要占用多少空间?
160亿个Byte , 1G = 1024 * 1024 * 1024 Byte 约等于10亿字节
所以大概16G
红黑树和哈希表在此基础上还要有自己的一些额外损耗,故不考虑
这道题最佳解法是位图
40亿个整数,每个数一个比特位来存,40亿个比特位,那就是5亿个字节,
又因为1G 约等于 10 亿个字节,所以40亿比特位就大概是0.5G也就是500M
因为存的是整数,有41亿多的数,所以我们开42亿个空间
fstring fscanf 读进位图,这是最优最快的做法
实现位图:
接口
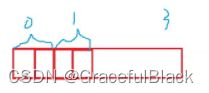
[set]算出在第几个整数,除8即可,算出i;要算出在该整数中的第几个比特位,模8即可,算出j(看图)
将某比特位置1:或等1左移j位(右边是低位左边是高位情况)
[reset]把某个位变成0,其他位不能影响。除了那个位是0,其他位是1,与一下,也就是1左移j位再取反
!逻辑取反,~是按位取反
[test]单纯的算一下第j位是0还是1呢,单纯与而不是与等不修改值,只是判断
最后返回让它隐式类型转换成bool值
库里有位图,可以直接用
开空间的时候最大可以开0xffffff,也可以开vector<-1>这样,因为把有符号整数看成无符号整数
就是最大,补码也就是全1
哈希表的时间复杂度为什么是O(1),怎么算出来的?
有n个桶,平均每个桶挂一个节点,那么就是O(1)
#pragma once
#include题1:
给定100亿个整数,设计算法找出只出现一次的数
一个整数4字节,100亿整数也就是400亿个byte,也就是40G内存
三种状态①出现0次②出现1次③出现2次及以上
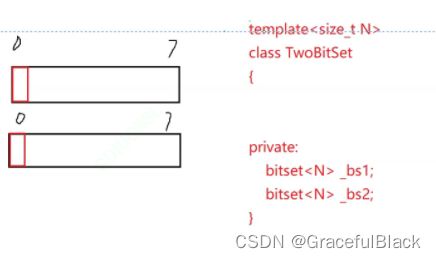
思路一:以前是一个位表示一个值,现在我们使用两个位表示一个值,这样重写有点烦
思路二:用两个位图,第一个位图的第i位与第二个位图的第i位合起来作两个比特位,简单写一下代码,
最后把bs1等于0,bs2等于1的找出来即可
#pragma once
#include题2:给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集
无论是100亿个整数还是1000亿个整数存到位图里都只需要500M
思路一:一个文件中的整数,set到一个位图,读取第二个文件的整数判断在不在位图,在的话就是交集,不在
的话就不是交集。
缺陷:交集会把重复值找出来,多次出现,最后的结果要想办法去重一下,刚开始就去重其实也是可以的
思路二:一个文件中的整数,set到一个位图bs1,另一个文件中整数,set到另一个位图bs2
a,遍历bs2中值,看在不在bs1,在就是交集
b,bs1中的值依次跟bs2中的值与一下,再去看与完是1的位置值就是交集
题3:位图应用变形:一个文件有100亿个int,1G内存,设计算法找到出现次数不超过两次的所有整数
四种情况①出现0次②出现1次③出现2次④出现3次及以上
只要找出情况2和情况3即可
如果题目改为不超过5次的位图,我们就需要3个位图
布隆过滤器
(布隆提出来的,故得此名)
位图:相比于红黑树,哈希表,节省空间,效率高
有局限性:只能处理整数
对于字符串,自定义类型对象,可以使用布隆过滤器
一个字符串转化成对应的一个整数
一定是会存在误判的,并且”在“的时候才会存在误判,”不在“的情况是准确的
实现布隆过滤器
首先需要一个位图(可以用库里的,也可以用自己写的)
每个值映射三个位置(不一定是三个),这样就不会容易冲突,只要有一个位置是0那就是”不在“,三个位置都为”1“
那就是都在
开布隆过滤器的N开多少?怎么样开比较合适?如何选择哈希函数个数和布隆过滤器的长度
知乎相关文章
k为哈希函数个数,m为布隆过滤器长度
k = m/n*ln2
非类型模板参数都是常量
测试一下误判率
相似字符串和不相似字符串其实不怎么影响错误率,X因子影响比较大
布隆过滤器到底如何减少误判?增加X因子的大小(跟调负载因子类似)
映射个数三个,五个即可,不建议更多
布隆过滤器不能保证没有误判
#pragma once
#include使用布隆过滤器的需求:数据量大,节省空间,允许误判,这样的场景,可以使用布隆过滤器
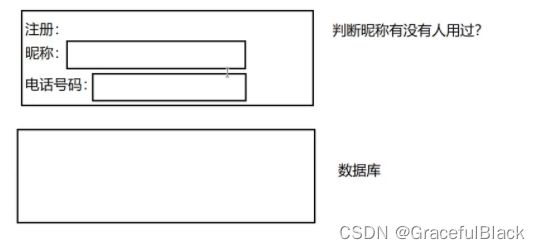
举例场景1:注册时候的昵称有无被使用 ,如果允许昵称偶然的误判,就没多大影响,
注册没被注册过的”昵称“一定是准确的,为了解决上面的一点误判,”昵称被使用“
的情况下再去数据库里进行查询
举例场景2:垃圾邮箱的判断
举例场景3:前端放一个布隆过滤器,过滤数据(”不存在“是准确的)
布隆过滤器扩展
题1:给两个文件,分别由100亿个query,我们只有1G内存,如何找到两个文件的交集,分别给出精确算法
和近似算法
交集里面 存在不是交集的 query ,这种思维下 布隆过滤器
query是字符串,比如 是sql语句,是网络请求url
假设每个query是10byte,100亿个query需要多少存储空间? --100G左右
->思路:哈希切分

如果Ai和Bi都太大,超过内存,可以考虑换个哈希算法,再切分一次
题2:如何扩展BloomFilter使得它支持删除元素的操作
不支持删除一个数,删除可能会影响其他值
建议方法:每个标记使用多个比特位,存储引用技术(有几个值映射了当前位置)
一般用8位比特位,实在溢出了用其他容器单独存储
上面支持删除,但是整体而言消耗空间变多了,布隆过滤器的优势下降了

题3:给一个超过100G的log file,log中存折IP地址,设计算法找出出现次数最多的IP地址?
哈希切分
依次读取ip,i = BKDRHash(ip) % 100
i是多少,ip就进入对应的编号i小文件中
相同的ip一定进入同一个小文件中,那么我们使用map统计一个小文件中的ip次数,就是他准确的次数
每一次更新都要把上一个map中的数据clear掉
比如说要找这些ip中最大的10个ip
pair
出现次数最多的10个ip, priority_queue
小堆找最大
拓展:一次性哈希