C++数据结构 —— 红黑树
目录
1.红黑树概念
2.红黑树节点的定义
3.红黑树的插入操作
4.红黑树的调整动作
4.1调整动作1
4.2调整动作2
4.3调整动作3
4.4插入算法的完整代码
4.5验证红黑树
4.6完整代码
1.红黑树概念
与AVL树一样,红黑树也是map、set等关联式容器的底层结构。但红黑树是现代主流的底层结构,STL使用的便是红黑树。其原因在于:AVL树保持平衡的方法太过于绝对(必须保证每个节点的左右子树的高度差不超过1),而红黑树的性质保证了其具有一定的"柔韧性"以及可观的效率。
红黑树的本质也是一颗二叉搜索树,但在原有的基础上做了平衡处理。红黑树的每个节点都会增加一个存储位,用来表示节点的颜色,可以是红色也可以是黑色。
红黑树具有以下几点性质:
1.每个节点不是红色就是黑色
2.根节点必须是黑色
3.如果一个节点是红色的,它的父节点或者两个子节点都必须为黑色
4.任何一条路径上的黑色节点数量都是相等的
5.空节点也认为是一颗红黑树,它也是假象的黑色
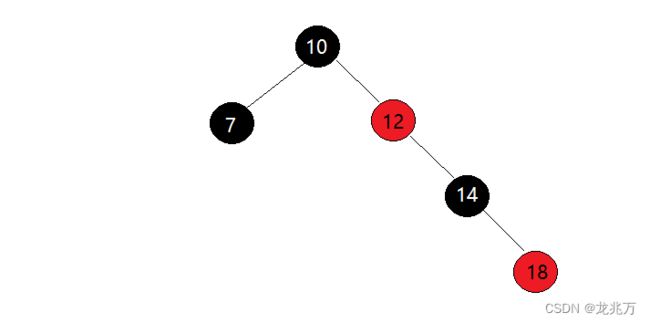
满足上面的条件之后,就能达到具有一定"柔韧性"的平衡:红黑树的最长路径的节点个数不会超过最短路径节点个数的两倍。其原因如下图:
2.红黑树节点的定义
enum Corlor //枚举颜色
{
RED,BLACK
};
template //为了方便,使用K模型
struct RBTreeNode
{
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
K _key;
Corlor _cor;
RBTreeNode(const K& key)
:_left(nullptr),_right(nullptr),_parent(nullptr),
_key(key),_cor(RED)
{}
}; 3.红黑树的插入操作
红黑树的插入方式与二叉搜索树一样,需要注意的是,插入的新节点的颜色可以红色,也可以是黑色,但是我们选择红色。因为如果新插入的节点是黑色,那么势必会破坏性质4,当红黑树有多条路径时,维护的成本会非常大。如果新插入的节点是红色,可以赌它的父节点是黑色,如果违反了性质3,我们仅需做一些微调即可。
template
class RBTree
{
typedef RBTreeNode Node;
public:
bool insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
_root->_cor = BLACK; //根节点的颜色必须是黑色
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(key);
cur->_cor = RED; //新插入的节点颜色为红色
if (key < parent->_key)
{
parent->_left = cur;
cur->_parent = parent;
}
else if (key > parent->_key)
{
parent->_right = cur;
cur->_parent = parent;
}
// 此时如果新插入的节点破坏了红黑树的性质,就必须做一些微调
while (parent && parent->_cor == RED)
{
// 调整动作
}
}
private:
Node* _root = nullptr;
}; 4.红黑树的调整动作
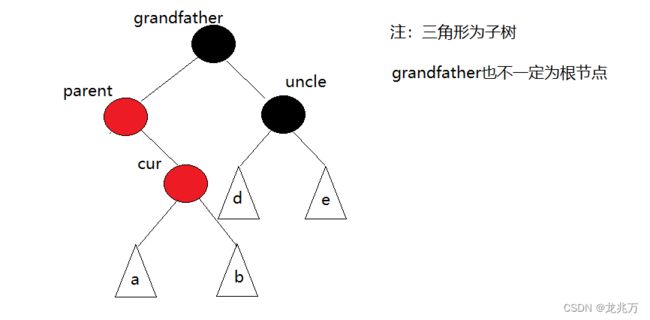
红黑树的调整分为三种动作, 需要调整的情况分别为:
1.cur为红色,parent为红色,gradfather(parent的父节点)为红色,并且uncle(parent的兄弟节点)节点存在且为红色
2.cur为红色,parent为红色,grandfather为黑色(这三个节点同在一侧),uncle存在且为黑色或uncle不存在
3.cur为红色,parent为红色,grandfather为黑色(这三个节点不在同一侧),uncle存在且为黑色或uncle不存在
4.1调整动作1
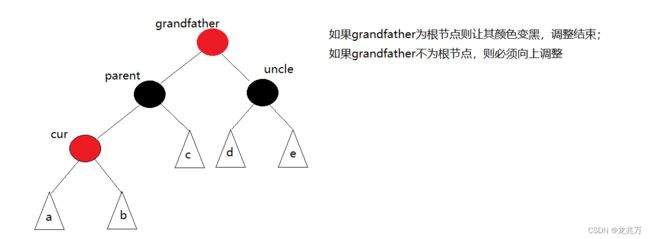
针对情况1, 可以做出如下调整动作:
1.让parent和uncle的颜色变黑
2.让grandfather的颜色变红
3.如果grandfather为根节点,则让其颜色变黑,结束调整;如果grandfather为某一子树,那么让cur = grandfather,parent = cur->_parent继续向上调整
4.2调整动作2
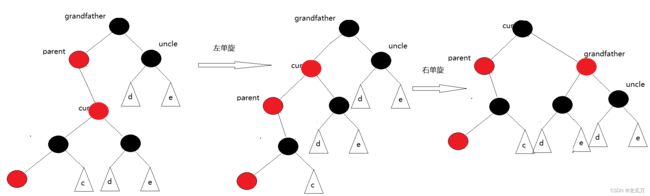
对于情况2,它是由情况1变过来的:
以这种情况为例,有AVL树的基础可以很明显的看出要以grandfather为轴进行一个右单旋;那么对应的,如果grandfather、parent、cur在右侧连成一线,就要使用左单旋。旋转完成之后,需要将parent置黑色,grandfather置红色。
4.3调整动作3
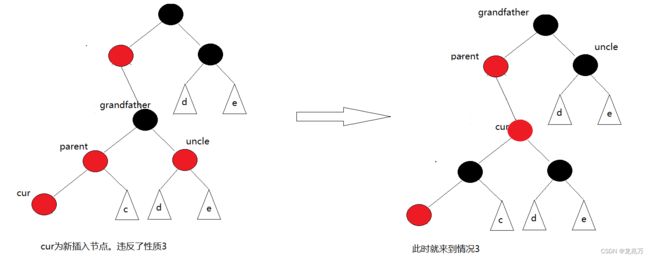
对于情况3,它是由情况1变过来的:
有过AVL树基础,可以明显的看出,此时要以parent为轴做一个左单旋;再以grandfather为轴做一个右单旋。事实上,当以parent为轴做一个左单旋时候,就立马回到了情况2。旋转完成之后,需要将cur置黑色,grandfather置红色。
综上,情况1可以转化为情况2或情况3,如果没有转化,证明调整结束;针对情况2,调整完毕即可结束;针对情况3,调整完毕即可结束。
4.4插入算法的完整代码
在调整红黑树时会使用旋转算法,AVL树中已经介绍过了。大家仅需把AVL树中的旋转算法的有关平衡因子的部分删除掉即可。
bool insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
_root->_cor = BLACK; //根节点的颜色必须是黑色
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(key);
cur->_cor = RED; //新插入的节点颜色为红色
if (key < parent->_key)
{
parent->_left = cur;
cur->_parent = parent;
}
else if (key > parent->_key)
{
parent->_right = cur;
cur->_parent = parent;
}
// 此时如果新插入的节点破坏了红黑树的性质,就必须做一些微调
while (parent && parent->_cor == RED)
{
// 调整动作
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_cor == RED)
{
// 情况1
parent->_cor = uncle->_cor = BLACK;
grandfather->_cor = RED;
cur = grandfather;
parent = cur->_parent;
}
else // unle不存在或uncle存在且为黑
{
if (parent->_left == cur)
{
// 情况2
RotateR(grandfather);
parent->_cor = BLACK;
grandfather->_cor = RED;
}
else if(parent->_right == cur)
{
// 情况3
RotateL(parent);
RotateR(grandfather);
cur->_cor = BLACK;
grandfather->_cor = RED;
}
break; //关键
}
}
else if (grandfather->_right == parent) //镜像即可
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_cor == RED)
{
parent->_cor = uncle->_cor = BLACK;
grandfather->_cor = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (parent->_right == cur)
{
// 情况2
RotateL(grandfather);
parent->_cor = BLACK;
grandfather->_cor = RED;
}
else if (parent->_left == cur)
{
// 情况3
RotateR(parent);
RotateL(grandfather);
cur->_cor = BLACK;
grandfather->_cor = RED;
}
break; //关键
}
}
}
_root->_cor = BLACK; //确保根节点颜色为黑色
return true;
}4.5验证红黑树
逐一验证红黑树的各个性质即可。
bool isRBTree()
{
if (_root == nullptr)
{
return true; //空树也可以是红黑树
}
if (_root->_cor != BLACK)
{
cout << "根节点不为黑色!" << endl;
return false; //根节点颜色不为黑色
}
// 计算任意一条路径的黑色节点数量
int black_cnt = 0;
Node* cur = _root;
while (cur)
{
if (cur->_cor == BLACK)
{
++black_cnt;
}
cur = cur->_left;
}
return __isRBTree(_root, 0, black_cnt);
}
bool __isRBTree(const Node* root, int cnt, int key)
{
if (root == nullptr)
{
if (cnt != key)
{
cout << "每条路径的黑色节点数量不相等!" << endl;
return false;
}
return true;
}
if (root->_cor == BLACK)
{
++cnt;
}
// 顺便判断是否存在连续的红节点
Node* parent = root->_parent;
if (parent && parent->_cor == RED && root->_cor == RED)
{
cout << "存在连续的红节点!" << endl;
return false;
}
return __isRBTree(root->_left, cnt, key) && __isRBTree(root->_right, cnt, key);
}4.6完整代码
红黑树