第十一届蓝桥杯大赛第二场省赛赛题 C++ 大学C组

试题A：约数个数

问题描述

  对于一个整数，能整除这个整数的数称为这个数的约数。
  例如：1，2，3，6都是6的约数。
  请问78120有多少个约数。

算法设计

  这里使用开平方减少程序复杂度，但要注意完全平方数的存在。

#include
#include 
int main(){
    using namespace std;
    int num = 78120;
    int m = sqrt(num);
    int count = 0;
    for (int i = 1; i <= m; ++i) {
        if(num % i == 0){
            count += 2; //约数一般是一对，所以递增2
        }
    }
    if( m * m == num){
        count --; //完全平方数有2个相同的约数，需要减1
    }
    cout << count << endl;
    return 0;
}

输出：

96

试题B：门牌制作

问题描述

  小蓝要为一条街的住户制作门牌号。
  这条街一共有2020位住户，门牌号从1到2020编号。
  小蓝制作门牌的方法是先制作0到9这几个数字字符，最后根据需要将字符粘贴到门牌上，例如门牌1017需要依次粘贴字符1、0、1、7，即需要1个字符0，2个字符1，1个字符7.
  请问要制作所有的1到2020号门牌，总共需要多少个字符2？

算法设计

  遍历1~2022，查找2出现的次数。

#include
int main(){
    using namespace std;
    int num = 2020;
    int count = 0;
    for (int j = 1; j <= num; ++j) {
        int temp = j;
        while(temp){
            int x;
            x = temp % 10;
            temp = temp/10;
            if(x == 2){
                count++;
            }
        }
    }
    cout << count << endl;
    return 0;
}

输出：

624

试题C：跑步锻炼

问题描述

  小蓝每天都锻炼身体。
  正常情况下，小蓝每天跑1千米。如果某天是周一或者月初（1日），为了激励自己，小蓝要跑2千米。如果同时是周一或月初，小蓝也是跑2千米。
  小蓝跑步已经坚持很长时间，从2000年1月1日周六（含）到2020年10月1日周四（含），请问这段时间小蓝总共跑步多少千米？

算法设计

  这里要注意平年闰年之分，还有如何通过求余得到星期。

#include
#include
using namespace std;
int main() {
    vector<int> Month = { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
    int mon;
    int s = 5; // 初始为星期六 以5表示 便于求余运算
    int ans = 0;
    for (int year = 2000; year <= 2020; ++year) { //年
        if (year % 400 == 0 || year % 4 == 0 && year % 100 != 0)
            Month[1] = 29;
        else Month[1] = 28;
        if (year == 2020)
            mon = 9;
        else mon = 12;
        for (int m = 0; m < mon; ++m) { // 月
            for (int d = 1; d <= Month[m]; ++d) { // 日
                if (d == 1 || s == 0) { // 1号或者星期一
                    ++ans;
                }
                ++ans;
                ++s;
                s %= 7;
            }
        }
    }
    ans += 2; // 十月一日跑2km
    cout << ans << endl;
    return 0;
}

输出：

8879

试题E：蛇形填数

问题描述

  小明用从1开始的正整数“蛇形”填充无限大的矩阵。

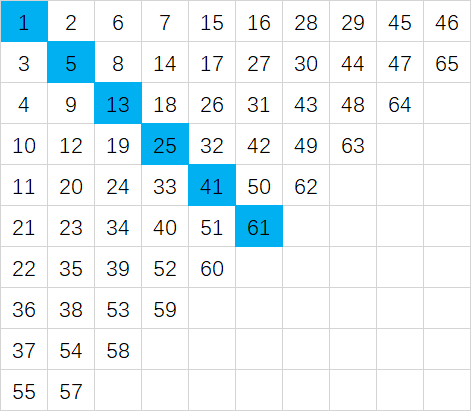
  容易看出矩阵第二行第二列中的数是5，请你计算矩阵中第20行第20列的数是多少？

算法设计

  找规律，1，5，13，25，41，61，中间的间隔都是4的倍数。

#include
using namespace std;
int main() {
    int bc = 4;
    int num = 1;
    for (int i = 1; i < 20; ++i) {
        num+=bc;
        bc += 4;
    }
    cout << num << endl;
    return 0;
}

输出：

761

试题F：成绩统计

问题描述：

  小蓝给学生们组织了一场考试，卷面总分为100分，每个学生的得分都是一个0到100的整数。
  如果得分至少是60分，则称为及格。如果得分至少为85分，则称为优秀。
  请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整数

输入格式

  输入的第一行包含一个整数n，表示考试人数。
  接下来n行，每行包含一个0至100的整数，表示一个学生的得分。

输出格式

  输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分四舍五入保留整数。

算法设计

  利用C++中库中round()函数进行四舍五入操作，其他按照题目意思就可以。

#include
#include 

using namespace std;
int main() {
    int n;
    scanf("%d",&n);
    int score[n];
    for (int i = 0; i < n; ++i) {
        scanf("%d",&score[i]);
    }
    int count_jg = 0,count_yx = 0;
    for (int i = 0; i < n; ++i) {
        if(score[i] >= 60){
            count_jg++;
        }
        if(score[i] >= 85){
            count_yx++;
        }
    }
    double jgl = double(count_jg)/n * 100;
    double yxl = double(count_yx)/n * 100;
    cout << round(jgl) <<"%"<< endl;
    cout << round(yxl) <<"%"<< endl;
    return 0;
}

输入：

7
80
92
56
74
88
100
0

输出：

71%
43%

试题G：单词分析

问题描述：

  小蓝正在学习一门神奇的语言，这门语言中的单词都是由小写英文字母组成，有些单词很长，远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词，他准备不再完全记忆这些单词，而是根据单词中哪个字母出现得最多来分辨单词。
  现在，请你帮助小蓝，给了一个单词后，帮助他找到出现最多的字母和这个字母出现的次数。

输入格式

  输入一行包含一个单词，单词只由小写英文字母组成。

输出格式

  输出由两行，第一行包含一个英文字母，表示单词中出现得最大的字母是哪个，如果有多个字母出现的次数相等，输出字典序列最小的那个。

算法设计

  利用C++中库memset函数对数组进行初始化，否则数组中残留元素会对结果产生影响。

#include
#include 

using namespace std;
int main() {
    string s;
    getline(cin,s);
    int len = s.size();
    int zm[27];
    memset(zm,0,sizeof(zm)); //将数组元素变为0
    for (int i = 0; i < len; ++i) {
        zm[s[i]-'a']++;
    }
    int max = 0;
    char ch;
    for (int i = 0; i < 27; ++i) {
        if(zm[i] > max){
            max = zm[i];
            ch = i;
        }
    }
    printf("%c\n",ch+'a');
    cout << max << endl;
    return 0;
}

输入：

longlonglongistoolong

输出：

o
6

试题H：数字三角形

问题描述

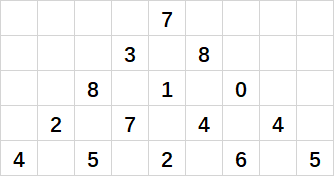
  上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径，对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。
  路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数，此外，先左下走的次数与向右下走的次数相差不能超过1.

输入格式：

  输入的第一行包含一个整数$N$（$1<N\le 100$），表示三角形的行数，下面的$N$行给出数字三角形，数字三角形上的数都是0至100之间的整数。

输出格式：

  输出一个整数，表示答案。

算法设计

dp[i][j]表示到达$(i,j)$处路径的最大值。

  当n是奇数时，相差的总次数不超过1，那么最后都会走到最后一层的中间那个数，即 ans=dp[n][n/2]。

  当n是偶数时，可能走到最后一层的中间那两个数的其中一个，这时候只需要比较一下那个比较大。

#include 
#include 

using namespace std;

int Max(int a,int b){
    return a>=b?a:b;
}
int main(){
    int n,ans;
    cin>>n;
    int dp[n+1][n+1];
    memset(dp,0, sizeof(dp)); //数组初始化
    for(int i=1;i<=n;i++){  //输入数字三角形
        for(int j=1;j<=i;j++)
            cin>>dp[i][j];
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++)
            dp[i][j]+=Max(dp[i-1][j],dp[i-1][j-1]);
    }

    if(n%2==0)
        ans=Max(dp[n][n/2],dp[n][n/2+1]);
    else
        ans=dp[n][n/2+1];
    cout<<ans;
    return 0;
}

输入：

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出：

27

试题I：作物杂交

问题描述

   作物杂交是作物栽培中重要的一步。已知有$N$种作物（编号1至$N$），第$i$种作物从播种到成熟的时间为$T_i$。作物之间两两可以进行杂交，杂交时间取两种中时间较长的一方。如作物$A$种植时间为5天，作物$B$种植时间为7天，则$AB$杂交花费的时间为7天。作物杂交会产生固定的作物，新产生的作物仍然属于$N$种作物中的一种。
   初始时，拥有其中$M$种作物的种子（数量无限，可以支持多次杂交）。同时可以进行多个杂交过程。求问对于给定的目标种子，最少需要多少天能够得到。
   如存在4种作物$ABCD$，各自的成熟时间为5天、7天、3天、8天。初始拥有$AB$两种作物的种子，目标种子为$D$，已知杂交情况为$A\times B\to C$，$A\times C\to D$。则最短的杂交过程为：
  第1天到第7天（作物B的时间），$A\times B\to C$。
  第8天到第12天（作物A的时间），$A\times C\to D$。
  花费12天得到作物$D$的种子。

输入格式

  输入的第1行包含4个整数$N$，$M$，$K$，$T$，$N$表示作物种类总数（编号1至$N$），$M$表示初始拥有的作物种子类型数量，$K$表示可以杂交的方案数，$T$表示目标种子的编号。
  第2行包含$N$个整数，其中第$i$个整数表示第$i$种作物的种植时间$T_i(1\le T_i\le 100)$。
  第3行包含$M$个整数，分别表示已拥有的种子类型$K_j(1\le K_j\le M)$，$K_j$两两不同。
  第4至$K+3$行，每行包含3个整数$A$，$B$，$C$，表示第$A$类作物和第$B$类作物杂交可以获得第$C$类作物的种子。

输出格式

  输出一个整数，表示得到目标种子的最短杂交时间。

算法设计

• 深度搜索算法

#include
#include
using namespace std;
void dfs(vector<int>& cost, vector<vector<pair<int, int> > >& hybrid, vector<int>& t, int target);
int main()
{
    int N, M, K, T; // 分别为作物种类总数、种子类型数量、杂交方案数、目标种子的编号
    cin >> N >> M >> K >> T;
    vector<int> t(N + 1); // 种植时间
    for (int i = 1; i <= N; ++i) {
        cin >> t[i]; // 编号1~N种子的种植时间
    }
    // 创建一个vector，元素个数为N+1，值均为INT_MAX
    vector<int> cost(N + 1, INT_MAX); // 花费总时间
    int tmp;
    for (int i = 0; i < M; ++i) { // 表示各编号的种子产生所需要的时间
        cin >> tmp;
        cost[tmp] = 0;
    }
    int a, b, c;
    // 采用pair对的形式表示方案
    vector<vector<pair<int, int> > > hybrid(N + 1); //杂交方案
    for (int i = 0; i < K; ++i) {
        cin >> a >> b >> c;
        // a和b杂交获得c
        pair<int, int> pa = make_pair(a, b);

        hybrid[c].push_back(pa);
    }
    // 搜索函数输入参数：已有种子集合，杂交方法，种子时间集合，目标种子编号
    dfs(cost, hybrid, t, T);
    cout << cost[T] << endl;
    return 0;
}
void dfs(vector<int>& cost, vector<vector<pair<int, int> > >& hybrid, vector<int>& t, int target) {
    // 查找能得到target的方法数
    for (int i = 0; i < hybrid[target].size(); i++) {
        int a = hybrid[target][i].first;
        int b = hybrid[target][i].second;
        if (cost[a] == INT_MAX) {
            dfs(cost, hybrid, t, a);
        }
        if (cost[b] == INT_MAX) {
            dfs(cost, hybrid, t, b);
        }
        cost[target] = min(cost[target], max(t[a], t[b]) + max(cost[a], cost[b]));
    }
}

输入：

6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6

输出：

16

试题J：子串分值和

问题描述

  对于一个字符串$S$，我们定义$S$的分值$f(S)$为$S$中出现的不同的字符个数。例如$f("aba")=2$，$f("abc")=3$，$f("aaa")=1$。
  现在给定一个字符串$S[0...n-1]$（长度为$n$），请你计算对于所有$S$的非空子串$S[i...j]$$(0\le i\le j<n)$，$f(S[i...j])$的和是多少。

输入格式

  输入一行包含一个由小写字母组成的字符串S。

输出格式

  输出一个整数表示答案。

算法设计

• 定义两个指针，分别遍历字符串，类似于字符串比较算法中的穷举算法。

# include 
using namespace std;
int ch[27] = {0};
int bts(char x);
int main(){
    string s;
    int temp = 0;
    int sum = 0;
    cin >> s;
    int n = s.size();
    for (int i = 0; i < n; ++i) {
        auto p = s.begin()+i;
        for(int j = 1; j <= n-i; j++){
            auto q = p + j;
            for (auto k = p; k != q; ++k) {
                temp = bts(*k);
            }
            memset(ch,0,sizeof(ch));
            sum = sum + temp;
        }
    }
    cout << sum;
}
int bts(char x){
    ch[x-'a']++;
    int count = 0;
    for (int i = 0; i < 27; ++i) {
        if(ch[i] != 0){
            count++;
        }
    }
    return count;
}

输入：

ababc

输出：

28