C#,码海拾贝(10)——三次样条(Cubic Spline)曲线插值算法,《C#数值计算算法编程》源代码升级改进版
样条曲线插值 Spline Interpolation
Spline interpolation similar to the Polynomial interpolation x’ uses low-degree polynomials in each of the intervals and chooses the polynomial pieces such that they fit smoothly together. The resulting function is called a spline.
类似于多项式插值x'的样条插值在每个区间中使用低阶多项式,并选择多项式片段,使它们平滑地拟合在一起。生成的函数称为样条曲线。
三次样条插值Cubic Spline Interpolation
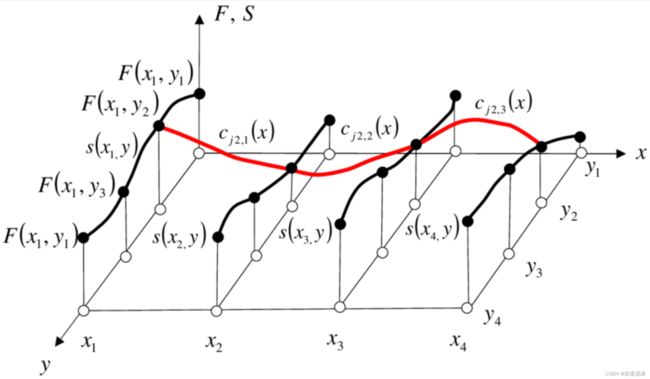
三次样条插值(Cubic Spline Interpolation)简称Spline插值,是通过一系列形值点的一条光滑曲线,数学上通过求解三弯矩方程组得出曲线函数组的过程。
实际计算时还需要引入边界条件才能完成计算。一般的计算方法书上都没有说明非扭结边界的定义,但数值计算软件如Matlab都把非扭结边界条件作为默认的边界条件。
Cubic spline interpolation is a way of finding a curve that connects data points with a degree of three or less. Splines are polynomial that are smooth and continuous across a given plot and also continuous first and second derivatives where they join.
We take a set of points [xi, yi] for i = 0, 1, …, n for the function y = f(x). The cubic spline interpolation is a piecewise continuous curve, passing through each of the values in the table.
- Following are the conditions for the spline of degree K=3:
- The domain of s is in intervals of [a, b].
- S, S’, S” are all continuous function on [a, b].
Here Si(x) is the cubic polynomial that will be used on the subinterval [xi, xi+1].
The main factor about spline is that it combines different polynomials and not use a single polynomial of degree n to fit all the points at once, it avoids high degree polynomials and thereby the potential problem of overfitting. These low-degree polynomials need to be such that the spline they form is not only continuous but also smooth.
But for the spline to be smooth and continuous, the two consecutive polynomials and Si (x) and Si+1 (x) must join at xi.
Or, Si (x) must be passed through two end-points:
Assume, S” (x) = Mi (i= 0,1,2, …, n). Since S(x) is cubic polynomial, so S” (x) is the linear polynomial in [xi, xi+1], then S”’ (x) will be:
By applying the Taylor series:
Let, x = xi+1:
Similarly, we apply above equation b/w range [xi-1, xi]:
Let hi =xi – xi-1
Now, we have n-1 equations, but have n+1 variables i.e M0, M1, M2,…Mn-1, Mn. Therefore, we need to get 2 more equation. For that, we will be using additional boundary conditions.
Let’s consider that we know S’ (x0) = f0‘ and S’ (xn) = fn‘, especially if S’ (x0) and S’ (xn) both are 0. This is called the clamped boundary condition.
Similarly, for Mn
or
Combining the above equation in to the matrix form, we get the following matrix。
以上文字凑数用,原理请阅读《C#数值计算算法编程》。
1、第一种边界条件的三次样条函数插值、导数与积分C#源代码
using System;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
namespace Zhou.CSharp.Algorithm
{
///
/// 插值计算类Interpolation.cs
/// 作者:周长发
/// 改编:深度混淆
/// https://blog.csdn.net/beijinghorn
///
public static partial class Interpolation
{
///
/// 第一种边界条件的三次样条函数插值、导数与积分
///
/// 一维数组,长度为n,存放给定的n个结点的值x(i),要求x(0)
/// 一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1
/// 一维数组,长度为n,调用时,dy(0)存放给定区间的左端点处的一阶导数值,dy(n-1)存放给定区间的右端点处的一阶导数值。返回时,存放n个给定点处的一阶导数值y'(i),i=0,1,...,n-1
/// 一维数组,长度为n,返回时,存放n个给定点处的二阶导数值y''(i),
/// 一维数组,长度为m,存放m个指定的插值点的值
/// 一维数组,长度为m,存放m个指定的插值点处的函数值
/// 一维数组,长度为m,存放m个指定的插值点处的一阶导数值
/// 一维数组,长度为m,存放m个指定的插值点处的二阶导数值
/// 指定函数的x(0)到x(n-1)的定积分值
public static double Spline3_Condition1(double[] x, double[] y, double[] dy, double[] ddy, double[] t, out double[] z, out double[] dz, out double[] ddz)
{
int n = x.Length;
int m = t.Length;
z = new double[m];
dz = new double[m];
ddz = new double[m];
// 初值
double[] s = new double[n];
s[0] = dy[0];
dy[0] = 0.0;
double h0 = x[1] - x[0];
for (int j = 1; j <= n - 2; j++)
{
double h1 = x[j + 1] - x[j];
double alpha = h0 / (h0 + h1);
double beta = (1.0 - alpha) * (y[j] - y[j - 1]) / h0;
beta = 3.0 * (beta + alpha * (y[j + 1] - y[j]) / h1);
dy[j] = -alpha / (2.0 + (1.0 - alpha) * dy[j - 1]);
s[j] = (beta - (1.0 - alpha) * s[j - 1]);
s[j] = s[j] / (2.0 + (1.0 - alpha) * dy[j - 1]);
h0 = h1;
}
for (int j = n - 2; j >= 0; j--)
{
dy[j] = dy[j] * dy[j + 1] + s[j];
}
for (int j = 0; j <= n - 2; j++)
{
s[j] = x[j + 1] - x[j];
}
for (int j = 0; j <= n - 2; j++)
{
double h1 = s[j] * s[j];
ddy[j] = 6.0 * (y[j + 1] - y[j]) / h1 - 2.0 * (2.0 * dy[j] + dy[j + 1]) / s[j];
}
{
double h1 = s[n - 2] * s[n - 2];
ddy[n - 1] = 6.0 * (y[n - 2] - y[n - 1]) / h1 + 2.0 * (2.0 * dy[n - 1] + dy[n - 2]) / s[n - 2];
}
double g = 0.0;
for (int i = 0; i <= n - 2; i++)
{
double h1 = 0.5 * s[i] * (y[i] + y[i + 1]);
h1 = h1 - s[i] * s[i] * s[i] * (ddy[i] + ddy[i + 1]) / 24.0;
g = g + h1;
}
for (int j = 0; j <= m - 1; j++)
{
int i = 0;
if (t[j] >= x[n - 1])
{
i = n - 2;
}
else
{
i = 0;
while (t[j] > x[i + 1])
{
i = i + 1;
}
}
double h1 = (x[i + 1] - t[j]) / s[i];
h0 = h1 * h1;
z[j] = (3.0 * h0 - 2.0 * h0 * h1) * y[i];
z[j] = z[j] + s[i] * (h0 - h0 * h1) * dy[i];
dz[j] = 6.0 * (h0 - h1) * y[i] / s[i];
dz[j] = dz[j] + (3.0 * h0 - 2.0 * h1) * dy[i];
ddz[j] = (6.0 - 12.0 * h1) * y[i] / (s[i] * s[i]);
ddz[j] = ddz[j] + (2.0 - 6.0 * h1) * dy[i] / s[i];
h1 = (t[j] - x[i]) / s[i];
h0 = h1 * h1;
z[j] = z[j] + (3.0 * h0 - 2.0 * h0 * h1) * y[i + 1];
z[j] = z[j] - s[i] * (h0 - h0 * h1) * dy[i + 1];
dz[j] = dz[j] - 6.0 * (h0 - h1) * y[i + 1] / s[i];
dz[j] = dz[j] + (3.0 * h0 - 2.0 * h1) * dy[i + 1];
ddz[j] = ddz[j] + (6.0 - 12.0 * h1) * y[i + 1] / (s[i] * s[i]);
ddz[j] = ddz[j] - (2.0 - 6.0 * h1) * dy[i + 1] / s[i];
}
return (g);
}
}
}
2、第二种边界条件的三次样条函数插值、导数与积分 C#源代码
///
/// 第二种边界条件的三次样条函数插值、导数与积分
///
/// 一维数组,长度为n,存放给定的n个结点的值x(i),要求x(0)
/// 一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1
/// 一维数组,长度为n,调用时,dy(0)存放给定区间的左端点处的一阶导数值,dy(n-1)存放给定区间的右端点处的一阶导数值。返回时,存放n个给定点处的一阶导数值y'(i),i=0,1,...,n-1
/// 一维数组,长度为n,返回时,存放n个给定点处的二阶导数值y''(i),
/// 一维数组,长度为m,存放m个指定的插值点的值
/// 一维数组,长度为m,存放m个指定的插值点处的函数值
/// 一维数组,长度为m,存放m个指定的插值点处的一阶导数值
/// 一维数组,长度为m,存放m个指定的插值点处的二阶导数值
/// 指定函数的x(0)到x(n-1)的定积分值
public static double Spline3_Condition2(double[] x, double[] y, double[] dy, double[] ddy, double[] t, double[] z, double[] dz, double[] ddz)
{
int n = x.Length;
int m = t.Length;
z = new double[m];
dz = new double[m];
ddz = new double[m];
// 初值
double[] s = new double[n];
dy[0] = -0.5;
double h0 = x[1] - x[0];
s[0] = 3.0 * (y[1] - y[0]) / (2.0 * h0) - ddy[0] * h0 / 4.0;
double h1 = 0.0;
for (int j = 1; j <= n - 2; j++)
{
h1 = x[j + 1] - x[j];
double alpha = h0 / (h0 + h1);
double beta = (1.0 - alpha) * (y[j] - y[j - 1]) / h0;
beta = 3.0 * (beta + alpha * (y[j + 1] - y[j]) / h1);
dy[j] = -alpha / (2.0 + (1.0 - alpha) * dy[j - 1]);
s[j] = (beta - (1.0 - alpha) * s[j - 1]);
s[j] = s[j] / (2.0 + (1.0 - alpha) * dy[j - 1]);
h0 = h1;
}
dy[n - 1] = (3.0 * (y[n - 1] - y[n - 2]) / h1 + ddy[n - 1] * h1 / 2.0 - s[n - 2]) / (2.0 + dy[n - 2]);
for (int j = n - 2; j >= 0; j--)
{
dy[j] = dy[j] * dy[j + 1] + s[j];
}
for (int j = 0; j <= n - 2; j++)
{
s[j] = x[j + 1] - x[j];
}
for (int j = 0; j <= n - 2; j++)
{
h1 = s[j] * s[j];
ddy[j] = 6.0 * (y[j + 1] - y[j]) / h1 - 2.0 * (2.0 * dy[j] + dy[j + 1]) / s[j];
}
{
h1 = s[n - 2] * s[n - 2];
ddy[n - 1] = 6.0 * (y[n - 2] - y[n - 1]) / h1 + 2.0 * (2.0 * dy[n - 1] + dy[n - 2]) / s[n - 2];
}
double g = 0.0;
for (int i = 0; i <= n - 2; i++)
{
h1 = 0.5 * s[i] * (y[i] + y[i + 1]);
h1 = h1 - s[i] * s[i] * s[i] * (ddy[i] + ddy[i + 1]) / 24.0;
g = g + h1;
}
for (int j = 0; j <= m - 1; j++)
{
int i = 0;
if (t[j] >= x[n - 1])
{
i = n - 2;
}
else
{
i = 0;
while (t[j] > x[i + 1])
{
i = i + 1;
}
}
h1 = (x[i + 1] - t[j]) / s[i];
h0 = h1 * h1;
z[j] = (3.0 * h0 - 2.0 * h0 * h1) * y[i];
z[j] = z[j] + s[i] * (h0 - h0 * h1) * dy[i];
dz[j] = 6.0 * (h0 - h1) * y[i] / s[i];
dz[j] = dz[j] + (3.0 * h0 - 2.0 * h1) * dy[i];
ddz[j] = (6.0 - 12.0 * h1) * y[i] / (s[i] * s[i]);
ddz[j] = ddz[j] + (2.0 - 6.0 * h1) * dy[i] / s[i];
h1 = (t[j] - x[i]) / s[i];
h0 = h1 * h1;
z[j] = z[j] + (3.0 * h0 - 2.0 * h0 * h1) * y[i + 1];
z[j] = z[j] - s[i] * (h0 - h0 * h1) * dy[i + 1];
dz[j] = dz[j] - 6.0 * (h0 - h1) * y[i + 1] / s[i];
dz[j] = dz[j] + (3.0 * h0 - 2.0 * h1) * dy[i + 1];
ddz[j] = ddz[j] + (6.0 - 12.0 * h1) * y[i + 1] / (s[i] * s[i]);
ddz[j] = ddz[j] - (2.0 - 6.0 * h1) * dy[i + 1] / s[i];
}
return (g);
}
3、第三种边界条件的三次样条函数插值、导数与积分 C#源代码
///
/// 第三种边界条件的三次样条函数插值、导数与积分
///
/// 一维数组,长度为n,存放给定的n个结点的值x(i),要求x(0)
/// 一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1
/// 一维数组,长度为n,调用时,dy(0)存放给定区间的左端点处的一阶导数值,dy(n-1)存放给定区间的右端点处的一阶导数值。返回时,存放n个给定点处的一阶导数值y'(i),i=0,1,...,n-1
/// 一维数组,长度为n,返回时,存放n个给定点处的二阶导数值y''(i),
/// 一维数组,长度为m,存放m个指定的插值点的值
/// 一维数组,长度为m,存放m个指定的插值点处的函数值
/// 一维数组,长度为m,存放m个指定的插值点处的一阶导数值
/// 一维数组,长度为m,存放m个指定的插值点处的二阶导数值
/// 指定函数的x(0)到x(n-1)的定积分值
public static double Spline3_Condition3(double[] x, double[] y, double[] dy, double[] ddy, double[] t, double[] z, double[] dz, double[] ddz)
{
int n = x.Length;
int m = t.Length;
z = new double[m];
dz = new double[m];
ddz = new double[m];
// 初值
double[] s = new double[n];
double h0 = x[n - 1] - x[n - 2];
double y0 = y[n - 1] - y[n - 2];
dy[0] = 0.0; ddy[0] = 0.0; ddy[n - 1] = 0.0;
s[0] = 1.0; s[n - 1] = 1.0;
double h1 = 0.0;
double alpha = 0.0;
double beta = 0.0;
for (int j = 1; j <= n - 1; j++)
{
h1 = h0;
double y1 = y0;
h0 = x[j] - x[j - 1];
y0 = y[j] - y[j - 1];
alpha = h1 / (h1 + h0);
beta = 3.0 * ((1.0 - alpha) * y1 / h1 + alpha * y0 / h0);
if (j < n - 1)
{
double u = 2.0 + (1.0 - alpha) * dy[j - 1];
dy[j] = -alpha / u;
s[j] = (alpha - 1.0) * s[j - 1] / u;
ddy[j] = (beta - (1.0 - alpha) * ddy[j - 1]) / u;
}
}
for (int j = n - 2; j >= 1; j--)
{
s[j] = dy[j] * s[j + 1] + s[j];
ddy[j] = dy[j] * ddy[j + 1] + ddy[j];
}
dy[n - 2] = (beta - alpha * ddy[1] - (1.0 - alpha) * ddy[n - 2]) / (alpha * s[1] + (1.0 - alpha) * s[n - 2] + 2.0);
for (int j = 2; j <= n - 1; j++)
{
dy[j - 2] = s[j - 1] * dy[n - 2] + ddy[j - 1];
}
dy[n - 1] = dy[0];
for (int j = 0; j <= n - 2; j++)
{
s[j] = x[j + 1] - x[j];
}
for (int j = 0; j <= n - 2; j++)
{
h1 = s[j] * s[j];
ddy[j] = 6.0 * (y[j + 1] - y[j]) / h1 - 2.0 * (2.0 * dy[j] + dy[j + 1]) / s[j];
}
h1 = s[n - 2] * s[n - 2];
ddy[n - 1] = 6.0 * (y[n - 2] - y[n - 1]) / h1 + 2.0 * (2.0 * dy[n - 1] + dy[n - 2]) / s[n - 2];
double g = 0.0;
for (int i = 0; i <= n - 2; i++)
{
h1 = 0.5 * s[i] * (y[i] + y[i + 1]);
h1 = h1 - s[i] * s[i] * s[i] * (ddy[i] + ddy[i + 1]) / 24.0;
g = g + h1;
}
for (int j = 0; j <= m - 1; j++)
{
h0 = t[j];
while (h0 >= x[n - 1])
{
h0 = h0 - (x[n - 1] - x[0]);
}
while (h0 < x[0])
{
h0 = h0 + (x[n - 1] - x[0]);
}
int i = 0;
while (h0 > x[i + 1])
{
i = i + 1;
}
double u = h0;
h1 = (x[i + 1] - u) / s[i];
h0 = h1 * h1;
z[j] = (3.0 * h0 - 2.0 * h0 * h1) * y[i];
z[j] = z[j] + s[i] * (h0 - h0 * h1) * dy[i];
dz[j] = 6.0 * (h0 - h1) * y[i] / s[i];
dz[j] = dz[j] + (3.0 * h0 - 2.0 * h1) * dy[i];
ddz[j] = (6.0 - 12.0 * h1) * y[i] / (s[i] * s[i]);
ddz[j] = ddz[j] + (2.0 - 6.0 * h1) * dy[i] / s[i];
h1 = (u - x[i]) / s[i];
h0 = h1 * h1;
z[j] = z[j] + (3.0 * h0 - 2.0 * h0 * h1) * y[i + 1];
z[j] = z[j] - s[i] * (h0 - h0 * h1) * dy[i + 1];
dz[j] = dz[j] - 6.0 * (h0 - h1) * y[i + 1] / s[i];
dz[j] = dz[j] + (3.0 * h0 - 2.0 * h1) * dy[i + 1];
ddz[j] = ddz[j] + (6.0 - 12.0 * h1) * y[i + 1] / (s[i] * s[i]);
ddz[j] = ddz[j] - (2.0 - 6.0 * h1) * dy[i + 1] / s[i];
}
return (g);
}
POWER BY 315SOFT.COM
基于坐标点的计算,从点集计算插值曲线等拓展方法请参阅《拉格朗日插值算法及其拓展》