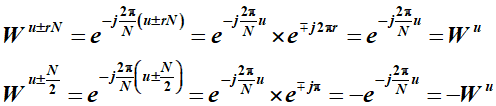（数字图像处理MATLAB+Python）第四章图像正交变换-第一节：离散傅里叶变换

一：一维离散傅里叶变换

（1）定义

一维离散傅里叶变换（Discrete Fourier Transform，DFT）：是一种数学技术，用于将代表离散时间信号的N个复数序列从时域转换到频域。DFT被广泛用于许多应用，如音频和图像处理、通信和控制系统。DFT是傅里叶变换的离散版本，傅里叶变换是一种用于分析频域信号的连续数学技术。DFT将信号表示为不同频率的复数正弦波之和，每个正弦波都有相关的幅度和相位。这些正弦波的频率是均匀的，由信号的采样率和长度决定。其定义式如下，该方程通过对时域中所有样本的贡献进行加总，计算出频率分量$u$在频域中的复数振幅，并以频率为$u$的复数指数函数加权

• $f(x)$是N个复数的序列，代表时域中的离散时间信号
• $F(u)$是N个复数的序列，代表频域中的同一信号
• 复指数函数$e^{-j\frac{2\pi ux}{N}}$的幅值为1，相位取决于频率$u$和时间指数$x$。它代表一个频率为$u$、相位与时间指数$x$成正比的正弦波。指数$-j$表示该波与参考信号是正交的，参考信号在零点时相位为零

$$F(u)=\sum _{x=0}^{N-1}f(x)e^{-j\frac{2\pi ux}{N}}u=0,1,2,\cdots ,N-1$$

一维逆向离散傅里叶变换（Inverse Discrete Fourier Transform, IDFT）：代表离散时间信号的复数序列从频域转回时域。IDFT是离散傅里叶变换（DFT）的逆运算，它是一种广泛使用的数学技术，用于分析和处理各种应用中的信号，如音频和图像处理、通信和控制系统。IDFT可用于从其频域表示中恢复原始时域信号，频域表示可通过对信号施加DFT获得。换句话说，IDFT允许我们将信号从频域转换回时域，这对进一步的处理或分析很有用。其定义式如下，IDFT定义方程将反离散傅里叶变换（IDFT）表示为不同频率的复指数函数之和

• $F(u)$是$N$个复数的序列，代表频域中的信号
• $f(x)$是N个复数的序列，代表时域中的同一信号

$$f(x)=\frac{1}{N}\sum _{u=0}^{N-1}F(u)e^{j\frac{2\pi ux}{N}}x=0,1,2,\cdots ,N-1$$

为了表示方便，我们$W=e^{-j\frac{2\pi }{N}}$，则DFT和IDFT可以表示为

$$\begin{array}{l}F(u)={\sum }_{x=0}^{N-1}f(x)W^{ux}u=0,1,2,\cdots ,N-1\\ f(x)=\frac{1}{N}{\sum }_{u=0}^{N-1}F(u)W^{-ux}x=0,1,2,\cdots ,N-1\end{array}$$

$W$因子具有周期性和对称性

（2）实例

对于一个长度为4的数字序列，求其DFT

$$F(u)=\sum _{x=0}^{3}f(x)W^{ux}=f(0)W^0+f(1)W^u+f(2)W^{2u}+f(3)W^{3u}$$

[ F ( 0 ) F ( 1 ) F ( 2 ) F ( 3 ) ] = [ W 0 W 0 W 0 W 0 W 0 W 1 W 2 W 3 W 0 W 2 W 4 W 6 W 0 W 3 W 6 W 9 ] [ f ( 0 ) f ( 1 ) f ( 2 ) f ( 3 ) ] \left[\begin{array}{l} F(0) \\ F(1) \\ F(2) \\ F(\mathbf{3}) \end{array}\right]=\left[\begin{array}{llll} W^{0} & W^{0} & W^{0} & W^{0} \\ W^{0} & W^{1} & W^{2} & W^{3} \\ W^{0} & W^{2} & W^{4} & W^{6} \\ W^{0} & W^{3} & W^{6} & W^{9} \end{array}\right]\left[\begin{array}{l} f(0) \\ f(1) \\ f(2) \\ f(3) \end{array}\right] ​F(0)F(1)F(2)F(3)​ ​= ​W0W0W0W0​W0W1W2W3​W0W2W4W6​W0W3W6W9​ ​ ​f(0)f(1)f(2)f(3)​ ​

根据$W$的对称性和周期性有

• 对称性
  • $W^2=-W^0$
  • $W^3=-W^1$
• 周期性
  • $W^4=W^0$
  • $W^6=W^2$
  • $W^9=W^1$

于是

( F ( 0 ) F ( 1 ) F ( 2 ) F ( 3 ) ) = ( W 0 W 0 W 0 W 0 W 0 W 1 − W 0 − W 1 W 0 − W 0 W 0 − W 0 W 0 − W 1 − W 0 W 1 ) ( f ( 0 ) f ( 1 ) f ( 2 ) f ( 3 ) ) = ( 1 1 1 1 1 W 1 − 1 − W 1 1 − 1 1 − 1 1 − W 1 − 1 W 1 ) ( f ( 0 ) f ( 1 ) f ( 2 ) f ( 3 ) ) = ( f ( 0 ) + f ( 2 ) + [ f ( 1 ) + f ( 3 ) ] f ( 0 ) − f ( 2 ) + [ f ( 1 ) − f ( 3 ) ] W 1 f ( 0 ) + f ( 2 ) − [ f ( 1 ) + f ( 3 ) ] f ( 0 ) − f ( 2 ) − [ f ( 1 ) − f ( 3 ) ] W 1 ) \left(\begin{array}{c} F(0) \\ F(1) \\ F(2) \\ F(3) \end{array}\right)=\left(\begin{array}{cccc} W^{0} & W^{0} & W^{0} & W^{0} \\ W^{0} & W^{1} & -W^{0} & -W^{1} \\ W^{0} & -W^{0} & W^{0} & -W^{0} \\ W^{0} & -W^{1} & -W^{0} & W^{1} \end{array}\right)\left(\begin{array}{c} f(0) \\ f(1) \\ f(2) \\ f(3) \end{array}\right)=\left(\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 1 & W^{1} & -1 & -W^{1} \\ 1 & -1 & 1 & -1 \\ 1 & -W^{1} & -1 & W^{1} \end{array}\right)\left(\begin{array}{c} f(0) \\ f(1) \\ f(2) \\ f(3) \end{array}\right)=\left(\begin{array}{c} f(0)+f(2)+[f(1)+f(3)] \\ f(0)-f(2)+[f(1)-f(3)] W^{1} \\ f(0)+f(2)-[f(1)+f(3)] \\ f(0)-f(2)-[f(1)-f(3)] W^{1} \end{array}\right) ​F(0)F(1)F(2)F(3)​ ​= ​W0W0W0W0​W0W1−W0−W1​W0−W0W0−W0​W0−W1−W0W1​ ​ ​f(0)f(1)f(2)f(3)​ ​= ​1111​1W1−1−W1​1−11−1​1−W1−1W1​ ​ ​f(0)f(1)f(2)f(3)​ ​= ​f(0)+f(2)+[f(1)+f(3)]f(0)−f(2)+[f(1)−f(3)]W1f(0)+f(2)−[f(1)+f(3)]f(0)−f(2)−[f(1)−f(3)]W1​ ​

二：一维快速傅里叶变换

（1）定义

一维快速傅里叶变化（Fast Fourier Transform, FFT）：FFT是快速傅里叶变换的缩写，它是计算$N$个复数序列的离散傅里叶变换（DFT）的一种有效算法。FFT算法将DFT的计算复杂度从$O(N^2)$降低到$O(NlogN)$，使其对实时信号处理应用非常实用。FFT的工作原理是利用DFT计算中使用的复数指数函数的对称性和周期性特性。通过巧妙地重新安排计算，FFT算法将DFT计算分成更小的子问题，这些子问题可以以分而治之的方式被递归解决。具体来说，将原函数分为奇数项和偶数项，通过不断的一个奇数一个偶数的相加（减），最终得到需要的结果，因此FFT是将复杂的运算变成两个数相加（减）的简单运算的重复

（2）实例

对于一个长度为8的数字序列，利用FFT算法求其DFT

$$F(u)=\sum _{x=0}^{7}f(x)W^{ux}=f(0)W^0+f(1)W^u+f(2)W^{2u}+f(3)W^{3u}+f(4)W^{4u}+f(5)W^{5u}+f(6)W^{6u}+f(7)W^{7u}$$

三：二维离散傅里叶变换

（1）定义

二维傅里叶变换（two-dimensional Fourier transform）：是一种数学运算，将一个二维函数从时域转换到频域。在二维傅里叶变换中，输入是一个二维函数$f(x,y)$，输出是一个描述输入函数的频率内容的函数$F(u,v)$。输出$F(u,v)$是一个复值函数，其中$F(u,v)$的幅度代表$(u,v)$处频率成分的振幅，$F(u,v)$的相位代表该成分的相移

如下，频域中的复值函数$F(u,v)$可以用每个频率分量$(u,v)$的振幅$|F(u,v)|$和相位角$\varphi (u,v)$表示。$F(u,v)$的实部和虚部$R(u,v)$和$I(u,v)$可用于计算每个频率分量$F(u,v)$的振幅和相位角

$$F(u,v)=R(u,v)+jI(u,v)=|F(u,v)|e^{j\phi (u,v)}$$

• 傅里叶谱：$|F(u,v)|=\sqrt{R^2(u,v)+I^2(u,v)}$
• 相位谱：$\phi (u,v)=\arctan \frac{I(u,v)}{R(u,v)}$
• 功率谱：$E(u,v)=|F(u,v){|}^2=R^2(u,v)+I^2(u,v)$

（2）程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• fft函数：计算一个向量或一个数组的一维快速傅里叶变换（FFT）
• ifft函数：计算一个向量或一个数组的一维快速傅里叶逆变变换（IFFT）
• fft2函数：计算一个矩阵的二维傅里叶变换
• ifft2函数：计算一个矩阵的二维傅里叶逆变换
• fftshift函数：将零频分量移到频谱中心。换句话说，它重新排列信号或图像的频域值，使零频分量位于频谱的中心。这对于可视化信号或图像的频率内容是很有用的。
• ifftshift函数：将零频率分量移回频谱的原点。这对于将移位后的频域信号或图像转换回其原始形式很有用

---

实现如下效果：频谱搬移图中间部分为低频部分，越靠外边频率越高。图像中的能量主要集中在低频区，高频能量很少或为零

这段MATLAB代码读入图像 “desert.jpg”，将其转换为灰度，使用fft2函数计算其二维离散傅里叶变换（DFT），并计算所得DFT的绝对值。然后，它使用最小-最大归一化将绝对DFT的值缩放到[0, 100]的范围内，并将这个缩放的DFT保存为ADFTI1。接下来，代码使用fftshift函数将DFT的零频分量移到频谱的中心。得到的移位后的DFT被保存为ADFTI2。最后，代码使用subplot和imshow来显示原始图像、其未缩放的DFT和其移位的DFT在1x3网格的子图中并排排列。总之，这段代码对输入图像进行了基本的频率分析，并将DFT和移位的DFT可视化

Image=imread('desert.jpg');%读取图像
grayI=rgb2gray(Image);%将彩色图像灰度化
DFTI1=fft2(grayI); % 二维离散傅里叶变换
ADFTI1=abs(DFTI1); % 获得其绝对值
top=max(ADFTI1(:));
bottom=min(ADFTI1(:));
ADFTI1=(ADFTI1-bottom)/(top-bottom)*100; % 使用max-min归一化，缩放至[0,100]
ADFTI2=fftshift(ADFTI1);%计算傅里叶变换并移位
subplot(131),imshow(Image),title('原图');%显示原图像
subplot(132),imshow(ADFTI1),title('原频谱图');%显示傅里叶变换频谱图
subplot(133),imshow(ADFTI2),title('移位频谱图');%显示傅里叶变换频谱图

Python实现：使用Python实现上述同样的功能

• cv2.dft函数：计算单通道（灰度）或多通道阵列的一维或二维离散傅里叶变换。这个函数支持正向和反向变换
• cv2.idft函数：计算单通道或多通道数组的反离散傅里叶变换
• cv2.fftshift函数：将一维或二维阵列的零频率分量移到频谱中心
• cv2.ifftshift函数：将一维或二维阵列的零频率分量移回频谱的原点

# Load the image
img = cv2.imread('desert.jpg')

# Convert to grayscale
gray_img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)

# Compute the 2D Discrete Fourier Transform
dft_img = np.fft.fft2(gray_img)

# Get the absolute values
abs_dft_img = np.abs(dft_img)

# Normalize using max-min normalization and scale to [0, 100]
top = np.max(abs_dft_img)
bottom = np.min(abs_dft_img)
abs_dft_img = ((abs_dft_img - bottom) / (top - bottom)) * 100

# Shift the Fourier Transform
shifted_dft_img = np.fft.fftshift(abs_dft_img)

# Plot the results using Matplotlib
fig, axs = plt.subplots(1, 3, figsize=(10, 5))
axs[0].imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
axs[0].set_title('Original Image')
axs[1].imshow(abs_dft_img, cmap='gray')
axs[1].set_title('Original Spectrum')
axs[2].imshow(shifted_dft_img, cmap='gray')
axs[2].set_title('Shifted Spectrum')
plt.show()

（3）性质

A：可分性

可分性：两个函数在空间域的乘积的傅里叶变换等于它们在频率域的傅里叶变换的卷积。在数学上，如果$f(x,y)$和$g(x,y)$是空间域中的两个函数，那么它们的乘积为

$$h(x,y)=f(x,y)\ast g(x,y)$$

$h(x,y)$的傅里叶变换是

$$H(u,v)=F\{h(x,y)\}=F\{f(x,y)\ast g(x,y)\}$$

利用傅里叶变换的卷积定理，我们可以将$H(u,v)$表示为

$$H(u,v)=F\{f(x,y)\}\ast F\{g(x,y)\}$$

因此，两个函数之积的傅里叶变换等于它们的傅里叶变换的卷积。这一属性在图像处理和计算机视觉中很有用，因为它允许我们在空间域中对图像进行复杂的操作，把它们转换到频域并在那里应用更简单的操作。例如，我们可以利用这一特性来实现线性滤波器，如平滑或锐化滤波器，这在频域中更容易定义

B：线性

线性：二维傅里叶变换的线性属性指出，函数的线性组合的傅里叶变换等于它们的傅里叶变换的同一线性组合。在数学上，如果$f1(x,y)$和$f2(x,y)$是空间域的两个函数，$a$和$b$是任意两个常数，那么我们有

$$F\{a\ast f1(x,y)+b\ast f2(x,y)\}=a\ast F\{f1(x,y)\}+b\ast F\{f2(x,y)\}$$

这一特性使我们可以很容易地将多个函数结合起来，并将傅里叶变换应用到所产生的函数上，而不是对每个函数进行单独的傅里叶变换，然后再将结果结合起来

C：周期性

周期性：二维傅里叶变换的周期性属性指出，一个周期性函数的傅里叶变换也是一个周期性函数，其周期相同。在数学上，如果$f(x,y)$是一个周期为$T$的周期性函数，那么它的傅里叶变换$F(u,v)$也是周期为$\frac{1}{T}$的。在处理具有重复模式或结构的图像时，这一属性特别有用，因为它允许我们轻松分析和处理这些模式的频率成分

D：几何变换性

几何变换性：

四：二维离散傅里叶变换的性质

五：离散傅里叶变换在图像处理中的应用