python蓝桥杯B组考前冲刺

平面切分

传送通道

初始平面数为1
平面中每添加一条直线，平面数+1
新添加的直线与已有的直线的交点个数为N, 平面数再+N
每增加一条直线增加一个平面，每增加一个交点也增加一个平面

def isintersect(k1,b1,k2,b2): #判断两条直线是否相交
    if k1!=k2:
        return True
    else:
        return False
def getpoint(k1,b1,k2,b2):
    #计算两条直线的交点
    x=(b2-b1)/(k1-k2)
    y=(k2*b1-k1*b2)/(k2-k1)
    return (x,y)
#def isin(x0,y0,k,b):
 #   #判断某点是否在某条直线上
  #  if y0==k*x0+b:
   #     return True
    #else:
     #   return False
N=int(input())
li=[list(map(int,input().split())) for i in range(N)]
exist=[] #记录平面中已经有的直线
res=1 #记录平面的个数，初始为1
for item in li:
    points=[] #记录新添加的直线和已有直线的交点
    if item in exist: #如果已经有这条直线就直接跳过
        continue
    for e in exist: #遍历已有直线
        if isintersect(item[0],item[1],e[0],e[1]):
            #如果新添加的直线和已有的直线相交
            #计算它们的交点并记录
            new=getpoint(item[0],item[1],e[0],e[1])
            if new not in points:
                points.append(new)
    res+=(len(points)+1)
    exist.append(item)
print(res)

路径

定义函数求最小公倍数：

两个数：a和b（lcm函数）
axb=最大公约数x最小公倍数
最大公约数的求法：（辗转消除法）
其实在math库中有math.lcm(a,b)求最小公倍数，但是在蓝桥杯会报错没有。

dp[i]　#i:结点编号1~2021 #dp[i]:当前结点到结点1的最短路径长度
dp[j]　#j:结点编号i+1~i+21 #dp[j]:当前结点到结点i的最短路径长度

def lcm(a,b):
    s=a*b
    while b:
        a,b=b,a%b
    return s//a
n=2021
dp=[float('inf')]*(n+1)
dp[1]=0
for i in range(1,n+1):
    for j in range(i+1,i+22):
        if j>n:
            break
        dp[j]=min(dp[j],dp[i]+lcm(i,j))
print(dp[n])

数字三角形

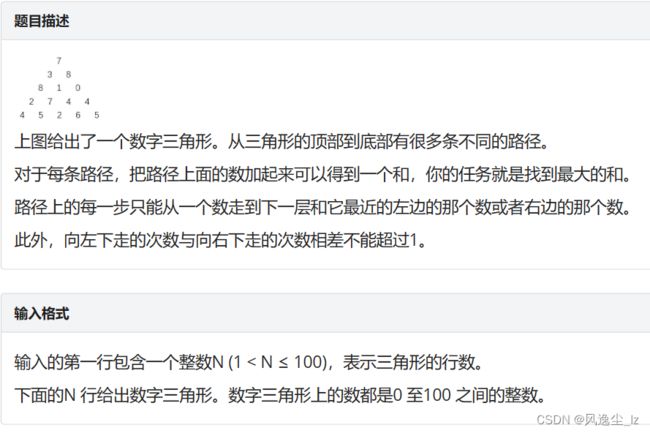
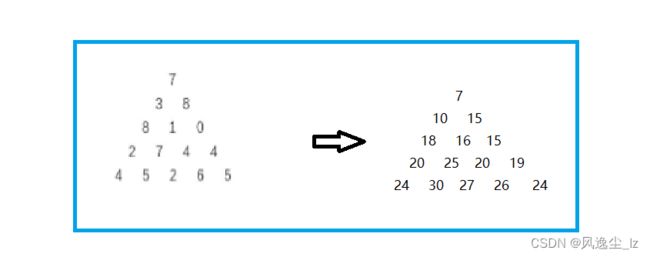
左右向下走的次数只差不超过1，也就以为着只能取中间，如果是奇数直接取中间值，如果是偶数行，则取中间较大值。

n=int(input())
a=[list(map(int,input().split())) for i in range(n)]
for i in range(1,n):
    for j in range(i+1):
        if j==0:  #最左边元素只能由右上方得到
            a[i][j]+=a[i-1][j]
        elif j==i:  #最右边元素只能由左上方得到
            a[i][j]+=a[i-1][j-1] 
        else:
            a[i][j]+=max(a[i-1][j-1],a[i-1][j]) #中间元素取上方相邻两个最大值
if n%2: #奇数行，返回中间值
    print(a[-1][n//2])
else:
    print(max(a[-1][n//2-1],a[-1][n//2]))
"""
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出：27
"""

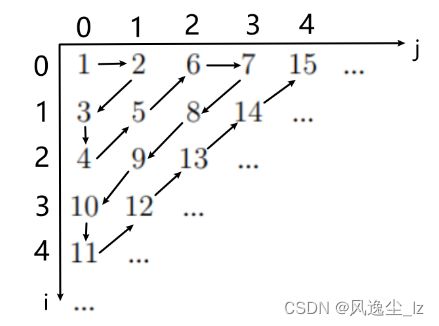
蛇形填数

可以建立一个空间直角坐标系，发现，坐标相加为奇数向左下方走，相加为偶数右上方走。

i,j,num=0,0,0 #初始化坐标和计数器
while True:
    num+=1
    if i==19 and j==19:
        break
    if (i+j)%2: #如果是奇数
        i+=1
        if j>0:
            j-=1
    else:
        j+=1
        if i>0:
            i-=1
print(num) #761

进制转换

一、其他进制转十进制：

2进制转10进制：

>>> int('1100',2)
12

8进制转10进制：

>>> int('12',8)
10

16进制转10进制：

>>> int('F',16)
15

二、十进制转其他进制

1.方式一：
bin()
oct()
hex()

>>> bin(2) #10进制转2进制
'0b10'
>>> oct(9) #10进制转8进制
'0o11'
>>> oct(15)
'0o17'
>>> hex(15) #10进制转16进制
'0xf'

format实现转换

>>> format(2,"b") # （10进制的）2转二进制
'10'
>>> format(9,"o") # （10进制的）9转八进制
'11'
>>> format(15,'x')
'f'

format(integer, ‘x’) 将integer转换为16进制，不带0x。integer为整型，‘x’可换为’o’,‘b’,'d’相对应八、二、十进制。
那么如何将2进制转换为16进制了，在纸上我们可以通过每次取四位作为一位，将2进制转16进制，也就是说1111 0000 (2)=F0(16),在python中，我们可以用int(‘11110000’,2)转10进制，再用10进制转16进制

>>> format(int('11110000',2),'x')
'f0'

一、Itertools.permutations

知识准备：
Python Itertools.Permutations()用法及代码示例 - 纯净天空 (vimsky.com)

1.马虎算式

from itertools import permutations
p=permutations(range(1,10),5)
num=0
for i in list(p):
  a,b,c,d,e=i
  if (a*10+b)*(c*100+d*10+e)==(a*100+d*10+b)*(c*10+e):
    num+=1
print(num)

方式二：

from itertools import permutations
count = 0
for i in permutations('123456789', 5):
    x = int(''.join(i[:2]))
    y = int(''.join(i[2:]))
    m = int(i[0]+i[3]+i[1])
    n = int(i[2]+i[4])
    if x*y == m*n:
      count += 1
print(count)

2.幻方

from itertools import permutations
for i in permutations([2,3,4,5,6,7,8,10,12,14]):
  if 16+i[0]+i[1]+13==i[2]+i[3]+i[4]+11==9+i[5]+i[6]+i[7]==i[8]+15+i[9]+1==16+i[2]+i[8]+9==i[0]+i[3]+i[5]+15==i[1]+11+i[6]+i[9]==13+i[4]+i[7]+1:
    print(i[7])
    break

二、itertools.combinations

combinations和permutations返回的是对象地址，原因是在python3里面，返回值已经不再是list,而是iterators（迭代器）, 所以想要使用，只用将iterator 转换成list 即可。
combinations方法重点在组合

combinations(p,r) p是一个list参数 r是数字，r长度的tuple，按顺序排列，没有重复元素

3.数字划分

from itertools import *
li=list(range(1,17))
sum1=sum(li)
sum2=sum([pow(i,2) for i in li])
sum3=sum([pow(i,3) for i in li])
for x in combinations(li,8):
  lx = list(x)
  if sum(lx)==sum1//2 and sum([i*i for i in lx])==sum2//2 and sum([i*i*i for i in lx])==sum3//2 and 1 in lx:
    for j in lx:
      print(j,end=' ')

一、datetime模块

datetime模块

1. isoweekday(…):
   返回符合ISO标准的指定日期所在的星期数（周一为1…周日为7)
   示例如下：

>>> a = datetime.date(2017,3,22)
>>> a.isoweekday()
3

2.timedelta()
timedelta类是用来计算二个datetime对象的差值的。
此类中包含如下属性：
1、days:天数
2、microseconds：微秒数(>=0 并且 <1秒）
3、seconds：秒数(>=0 并且 <1天）

1.星期一

from datetime import *
num=0
start=date(1901,1,1)
end=date(2000,12,31)
while start<=end:
  if start.weekday()==0:
    num+=1
  start+=timedelta(days=1)
print(num)

2.星系炸弹

from datetime import *
# start=date(2014,11,9)
# start+=timedelta(days=1000)
# print(format(start))
print(format(date(2014,11,9)+timedelta(days=1000)))

二、calendar模块

calendar详解

常用：

1.isleap(year):判断是否为闰年：

import calendar
print(calendar.isleap(2023)) #2023年是平年，返回False
print(calendar.isleap(2024)) #2024年是润年，返回True

2.leapdays(y1,y2):返回y1和y2之间的闰年数量：(包含起始年，不包含结束年）

import calendar
print(calendar.leapdays(2000,2024))

3.weekday(year,month,day):获取指定日期为星期几

import calendar
print(calendar.weekday(2023,3,27)) # 0   是指星期一

4.monthrange(year,month):返回一个由一个月第一天的星期和当前月的天数组成的元组

import calendar
print(calendar.monthrange(2023,3)) #返回(2,31) 表示2023年3月的第一天为星期三，这个月有31天

1.天数

import calendar
m=int(input())
print(calendar.monthrange(2021,m)[1])

单词分析

1.单词分析

word=input()
Max=0   
#找出数目最大的字母
for s in word:
  if word.count(s)>Max:
    Max=word.count(s)
#找出所有为Max数目的字母
New=[]
for s in word:
  if word.count(s)==Max:
    New.append(s)
New.sort()
print(New[0])
print(Max)

解法2：

a=input()
dicts={}
for i in a:
    dicts[i]=dicts.get(i,0)+1
l = sorted(dicts.items(), key= lambda x:[x[1],-ord(x[0])])
print(l[-1][0])
print(l[-1][1])
成绩统计 - 蓝桥云课 (lanqiao.cn)
n=int(input())
a=[int(input()) for i in range(n)]
def f(x):
  return format(100*len([i for i in a if i>=x])/n,'.0f')+'%'
print(f(60),f(85),sep='\n')

成绩统计

成绩统计

输入：
7
80
92
56
74
88
100
0
输出：
71%
43%

n=int(input())
a=[int(input()) for i in range(n)]
def f(x):
  return format(100*len([i for i in a if i>=x])/n,'.0f')+'%'
print(f(60),f(85),sep='\n')

1.快速幂

1.1 快速幂

1.2 快速幂求逆元

"""
基本思想：
    求逆元的本质是，给定一个数a，求出一个x，使得a*x=1 (mod p)，其中x就被称为逆元;
    根据费马定理，当p为质数时，a^(p-1)=1 (mod p),即a*a^(p-2)=1 (mod p),所以a^(p-2)就为我们要求的a的逆元
"""
def qmi(a,k,p):
    res=1
    while k:
        if k&1==1:
            res=res*a%p 
        k>>=1
        a=a*a%p 
    return res
n=int(input())
while n:
    n-=1
    a,p=map(int,input().split())
    res=qmi(a,p-2,p)
    if a%p!=0:
        print(res)
    else:
        print("impossible") #若a是p的倍数，则a与p不互质，此时a*x是p的倍数，a*x%p==0