C++程序员修炼手册--红黑树的实现及map和set的封装
目录
一,概述
1,有了二叉搜索树,为什么还需要AVL树
2,有了AVL树,为什么还需要红黑树
二,红黑树的性质
三,红黑树模拟实现
1,树节点的构造
2,树的插入操作
1,首先构造根节点,再去插入数据
2,插入数据
3,调节树的平衡
四,迭代器的实现
4.1,红黑树的迭代器怎么走
4.2 迭代器的封装
1,构造出一个迭代器的类,通过对类的操作,实现对树的节点的访问
2,反向迭代器的封装
五,set和map的封装
5.1,set的封装
5.2,map的封装
六,总代码如下所示:
1.RBtree
2.map.h
3,set.h
4,Iterator.h
期待关注,一键三连
一,概述
1,有了二叉搜索树,为什么还需要AVL树
二叉搜索树在极端条件下,会退化成一条单链表,增删查改效率会退化到Olog(n),严重影响性能,而AVl树通过对结点的旋转,会形成一个左右子树高度差不超过1的搜索树,形成一个高度平衡的二叉树。
2,有了AVL树,为什么还需要红黑树
AVL树在增删数据时,会通过不停的旋转来实现树的平衡,在频繁的增删数据时,几乎都需要旋转,效率退化,而使用红黑树,通过牺牲不是特别平衡的树,可以减少树的旋转,通过节点颜色的改变和树的旋转共同维持树的平衡,虽然没有AVL树高度平衡,但效率会变高。
二,红黑树的性质
1,是一个二叉搜索树,左树值比根节点值小,右树值比根节点大。
2,根节点是黑色
3,没有连续的红色节点
4,每条路径上的黑色节点数相等
5,最长路径不超过最短路径的2倍
三,红黑树模拟实现
1,树节点的构造
通过使用三叉链来实现,节点颜色通过枚举实现(RED,BLACK)
enum Color
{
RED,
BLACK,
};
template
struct RBtreenode
{
RBtreenode*_left; //左节点
RBtreenode*_right; //右节点
RBtreenode*_parent;//父节点
pair_kv; //数据
Color _col; //颜色
RBtreenode(const pair&kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(RED)//默认给红色
{}
}; 2,树的插入操作
1,首先构造根节点,再去插入数据
template
class RBtree
{
typedef RBtreenodenode;//对节点进行重定义
public:
pairinsert(const pair& kv)
{
}
private:
node*_root; //定义根节点
}; 2,插入数据
按照搜索二叉树的规则,先找到插入的位置,把数据插入进去,再对节点进行判断,看是否满足红黑树的性质,满足,直接返回,不满足,再对树进行处理
template
class RBtree
{
typedef RBtreenodenode;//对根节点进行重定义
public:
pairinsert(const pair& kv)
{
if(_root==nullptr)//根节点为空
{
_root=new node(kv);
_root->_col=BLACK;
return make_pair(_root,true);
}
node*parent=nullptr;
node*cur=_root;
//找到节点插入的位置
while(cur)
{
if(cur->_kv.first_right;
}
else if(cur->_kv.first>kv.first)
{
parent=cur;
cur=cur->_left;
}
else
{
return make_pair(cur,false);
}
}
//插入数据
node *newnode=new node(kv);
newnode->_col=RED;
//此时cur走到空,父亲走到将要插入的位置,插入数据
if(parent->_kv.first>kv.first)
{
parent->_left=newnode;
newnode->_parent=parent;
}
else
{
parent->_right=newnode;
newnode->_parent=parent;
}
cur=newnode;
//调节树的平衡
//重点,难点
while(parent&&parent->_col==RED)
{
}
}
private:
node*_root; //定义根节点
}; 3,调节树的平衡
3.1,父亲在祖父的左边
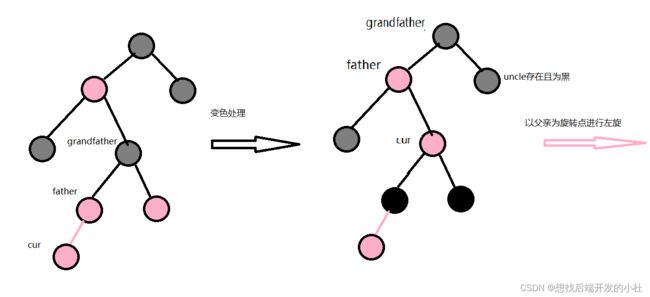
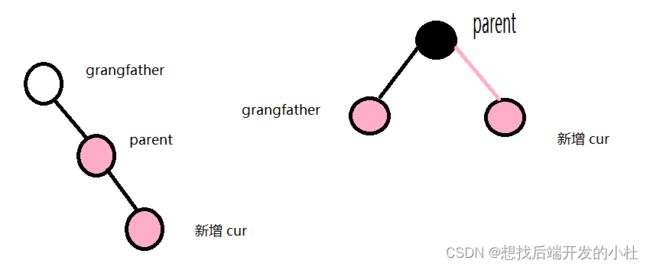
情况1,叔叔存在且为红
具象图如下所示:
代码如下:
node*grandfather=parent->_parent;
//父亲在祖父的左边
if(parent==grandfather->_left)
{
//关键看叔叔
//1,叔叔存在且为红
node*uncle=grandfather->_right;
if(uncle&&uncle->_col==RED)
{
//把父亲和叔叔变黑,祖父变红
uncle->_col=parent->_col=BLACK;
grandfather->_col=RED;
//此时往上处理,祖父的父亲可能为红,不满足红黑树性质,继续调整
cur=grandfather;
parent=grandfather->_parent;
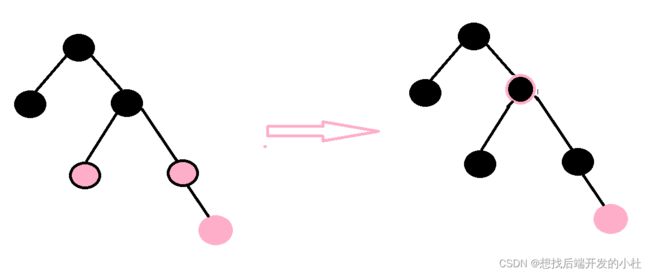
} 情况二,叔叔不存在,
//情况2,叔叔不存在
if(cur==parent->_left)
{
//右单旋处理
RoateR(grandfather);
parent->_col=BLACK;
grandfather->_col=RED;
}
//右旋
void RoateR(node*parent)
{
node*subL=parent->_left;
node*subLR=subL->_right;
//链接
parent->_left=subLR;
if(subLR)
{
subLR->_parent=parent;
}
subL->_right=parent;
//判断parent是否为根
node*parentparent=parent->_parent;
parent->_parent=subL;
if(parent==_root)
{
_root=subL;
subL->_parent=nullptr;
}
//不是根处理
else
{
if(parentparent->_left==parent)
parentparent->_left=subL;
else
parentparent->_right=subL;
subL->_parent=parentparent;
}
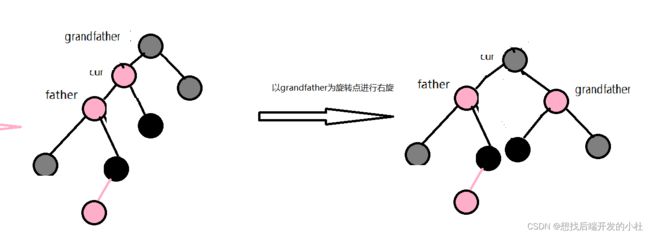
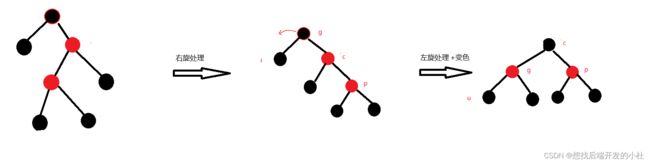
}情况三,叔叔存在且为黑
当在此种情况下,双旋处理+变色,树平衡
//情况3,叔叔存在且为黑
else
{
RoateL(parent);
RoateR(grandfather);
grandfather->_col=RED;
cur->_col=BLACK;
}
3.2,父亲在祖父的右边
node*uncle=grandfather->_left;
//情况1,叔叔存在且为红
if(uncle&&uncle->_col==RED)
{
parent->_col=uncle->_col=BLACK;
grandfather->_col=RED;
//继续往上处理
cur=grandfather;
parent=cur->_parent;
} //叔叔不存在
if(cur==parent->_right)
{
RoateL(grandfather);
parent->_col=BLACK;
grandfather->_col=RED;
}情况三,叔叔存在且为黑
//叔叔为黑
else
{
RoateR(parent);
RoateL(grandfather);
grandfather->_col=RED;
cur->_col=BLACK;
}最后整个的插入操作就完成了,实现代码如下:
//插入数据
pairinsert(const pair&kv)
{
//如果树为空
if(_root==nullptr)
{
_root=new node(kv);
_root->_col=BLACK;
return make_pair(_root,true);
}
//树不为空
node*parent=nullptr;
node*cur=_root;
//找到节点插入的位置
while(cur)
{
if(cur->_kv.first_right;
}
else if(cur->_kv.first>kv.first)
{
parent=cur;
cur=cur->_left;
}
else
{
return make_pair(cur,false);
}
}
//插入数据
node*newnode=new node(kv);
newnode->_col=RED;
if(parent->_kv.first>kv.first)
{
parent->_left=newnode;
newnode->_parent=parent;
}
else
{
parent->_right=newnode;
newnode->_parent=parent;
}
cur=newnode;
//处理颜色
while(parent&&parent->_col==RED)
{
node*grandfather=parent->_parent;
//关键看叔叔
//父亲在祖父左边
if(parent==grandfather->_left)
{
//情况1,叔叔存在且为红
node*uncle=grandfather->_right;
if(uncle&&uncle->_col==RED)
{
parent->_col=uncle->_col=BLACK;
grandfather->_col=RED;
//继续往上处理
cur=grandfather;
parent=cur->_parent;
}
//情况2,叔叔不存在或者存在为黑
else
{
//叔叔不存在,单旋处理
if(cur==parent->_left)
{
RoateR(grandfather);
grandfather->_col=RED;
parent->_col=BLACK;
}
//情况三 ,叔叔存在且为黑
else
{
RoateL(parent);
RoateR(grandfather);
cur->_col=BLACK;
grandfather->_col=RED;
}
break;
}
}
//父亲在祖父右边
else
{
node*uncle=grandfather->_left;
//情况1,叔叔存在且为红
if(uncle&&uncle->_col==RED)
{
parent->_col=uncle->_col=BLACK;
grandfather->_col=RED;
//继续往上处理
cur=grandfather;
parent=cur->_parent;
}
//情况2,叔叔不存在或者叔叔为黑
else
{
//叔叔不存在
if(cur==parent->_right)
{
RoateL(grandfather);
parent->_col=BLACK;
grandfather->_col=RED;
}
//叔叔为黑
else
{
RoateR(parent);
RoateL(grandfather);
grandfather->_col=RED;
cur->_col=BLACK;
}
break;
}
}
}
_root->_col=BLACK;
return make_pair(cur,true);
}
//右旋
void RoateR(node*parent)
{
node*subL=parent->_left;
node*subLR=subL->_right;
//链接
parent->_left=subLR;
if(subLR)
{
subLR->_parent=parent;
}
subL->_right=parent;
//判断parent是否为根
node*parentparent=parent->_parent;
parent->_parent=subL;
if(parent==_root)
{
_root=subL;
subL->_parent=nullptr;
}
//不是根处理
else
{
if(parentparent->_left==parent)
parentparent->_left=subL;
else
parentparent->_right=subL;
subL->_parent=parentparent;
}
}
void RoateL(node*parent)
{
node*subR=parent->_right;
node*subRL=subR->_left;
parent->_right=subRL;
if(subRL)
{
subRL->_parent=parent;
}
//判断parent是否为根
subR->_left=parent;
node*parentparent=parent->_parent;
parent->_parent=subR;
if(_root==parent)
{
_root=subR;
subR->_parent=nullptr;
}
else
{
if(parentparent->_left==parent)
{
parentparent->_left=subR;
}
else
{
parentparent->_right=subR;
}
subR->_parent=parentparent;
}
} 四,迭代器的实现
4.1,红黑树的迭代器怎么走
从最左边的第一个元素,以中序遍历的方式向下走
++方式应为 {1 ,8,11,13 ,15,17,25}
--方式应为 {25,17,15,13,11,8,1}
其实现方式如下代码所示:
operator++()
从最左节点开始走,走父亲,右孩子,然后向上继续走,直到走到空
self operator++()
{
//如果右树不为空,走左子树的最左节点
if(_node->_right)
{
node*left=_node->_right;
while(left->_left)
{
left=left->_left;
}
_node=left;
}
//右子树为空,找孩子不是右的节点返回
else
{
node*cur=_node;
node*parent=cur->_parent;
while(parent&&cur==parent->_right)
{
cur=cur->_parent;
parent=parent->_parent;
}
_node=parent;
}
return *this;
}operator--()l类似上面++,先走右子树,再走父亲,走左子树
self operator--()
{
//如果左树不为空,找右子树的最右节点
if(_node->_left)
{
node*right=_node->_left;
//访问右子树的最右节点
while(right->_right)
{
right=right->_left;
}
_node=right;
}
else
{
//右树访问完,访问左树
node*cur=_node;
node*parent=cur->_parent;
while(parent&&cur==parent->_left)
{
cur=parent;
parent=parent->_parent;
}
_node=parent;
}
return *this;4.2 迭代器的封装
1,构造出一个迭代器的类,通过对类的操作,实现对树的节点的访问
//构造迭代器类型
template
struct __TreeIterator
{
typedef Ref reference;
typedef Ptr pointer;
typedef RB_treeNode node;
typedef __TreeIterator self;
node *_node;
__TreeIterator(node*node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const self &s) const
{
return _node!=s._node;
}
self operator++()
{
//如果右树不为空,走左子树的最左节点
if(_node->_right)
{
node*left=_node->_right;
while(left->_left)
{
left=left->_left;
}
_node=left;
}
//右子树为空,找孩子不是右的节点返回
else
{
node*cur=_node;
node*parent=cur->_parent;
while(parent&&cur==parent->_right)
{
cur=cur->_parent;
parent=parent->_parent;
}
_node=parent;
}
return *this;
}
self operator--()
{
//如果左树不为空,找右子树的最右节点
if(_node->_left)
{
node*right=_node->_left;
//访问右子树的最右节点
while(right->_right)
{
right=right->_left;
}
_node=right;
}
else
{
//右树访问完,访问左树
node*cur=_node;
node*parent=cur->_parent;
while(parent&&cur==parent->_left)
{
cur=parent;
parent=parent->_parent;
}
_node=parent;
}
return *this;
}
}; 2,反向迭代器的封装
++和--调用已有数据结构的--和++
实现反向迭代器
template
struct ReverseIterator
{
//红黑树中实例化以后再实例化反向迭代器
typedef typename Iterator::reference Ref;
typedef typename Iterator::pointer Ptr;
typedef ReverseIterator Self;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{}
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
bool operator!=(const Self& s) const
{
return _it != s._it;
}
bool operator==(const Self& s) const
{
return _it == s._it;
}
}; 五,set和map的封装
5.1,set的封装
1,红黑树存的是键值对,怎么传数据给pair
通过传的两个参数都为K,红黑树插入和find通过set定义的仿函数,提取到节点存取的值,再去比较,是一种高级的泛型编程。
template
class set
{
//仿函数,提取节点存取的值
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBtree::iterator iterator;
//实例化参数以后再去实例化迭代器
typedef typename RBtree::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
bool insert(const K& k)
{
_t.Insert(k);
return true;
}
private:
RBtree _t;
}; 5.2,map的封装
与set一样,都是通过仿函数拿到节点的值,再在插入和find中通过比较存取值
代码如下:
template
class map
{
//仿函数,拿出传过去参数的值
struct mapKeyOfT
{
const K& operator()(const pair& kv)
{
return kv.first;
}
};
public:
//在对象实例化以后,再去构造迭代器
typedef typename RBtree,mapKeyOfT>::iterator iterator;
typedef typename RBtree,mapKeyOfT>::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
bool insert(const pair& kv)
{
_t.Insert(kv);
return true;
}
private:
RBtree,mapKeyOfT> _t; 走到这里,基本map和set就结束了,其中最重要的应当是红黑树的插入操作(主要看叔叔)和operator++(中序遍历,看节点有没有右节点)
六,总代码如下所示:
1.RBtree
#pragma once
#include
#include
#include"iterator.h"
using namespace std;
enum Color
{
RED,
BLACK,
};
//构造节点类型
//使用T代表类型,传过来单参,就是set
//传过来键值对,就是map
template
struct RB_treeNode
{
RB_treeNode*_left;
RB_treeNode*_right;
RB_treeNode*_parent;
T _data;
Color _col;
RB_treeNode(const T& x)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_data(x)
,_col(RED)
{}
};
//构造迭代器类型
template
struct __TreeIterator
{
typedef Ref reference;
typedef Ptr pointer;
typedef RB_treeNode node;
typedef __TreeIterator self;
node *_node;
__TreeIterator(node*node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const self &s) const
{
return _node!=s._node;
}
self operator++()
{
//如果右树不为空,走左子树的最左节点
if(_node->_right)
{
node*left=_node->_right;
while(left->_left)
{
left=left->_left;
}
_node=left;
}
//右子树为空,找孩子不是右的节点返回
else
{
node*cur=_node;
node*parent=cur->_parent;
while(parent&&cur==parent->_right)
{
cur=cur->_parent;
parent=parent->_parent;
}
_node=parent;
}
return *this;
}
self operator--()
{
//如果左树不为空,找右子树的最右节点
if(_node->_left)
{
node*right=_node->_left;
//访问右子树的最右节点
while(right->_right)
{
right=right->_left;
}
_node=right;
}
else
{
//右树访问完,访问左树
node*cur=_node;
node*parent=cur->_parent;
while(parent&&cur==parent->_left)
{
cur=parent;
parent=parent->_parent;
}
_node=parent;
}
return *this;
}
};
//构造树
//Ref代表引用,ptr代表指针
//template
template
class RBtree
{
typedef RB_treeNode node;
public:
typedef __TreeIterator < T, const T&, const T* > const_iterator;
typedef __TreeIterator < T, T&, T* > iterator;
typedef ReverseIterator reverse_iterator;
reverse_iterator rbegin()
{
node* right = _root;
while (right && right->_right)
{
right = right->_right;
}
return reverse_iterator(iterator(right));
}
reverse_iterator rend()
{
return reverse_iterator(iterator(nullptr));
}
//最左边的元素
iterator begin()
{
node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
//最右边的元素
iterator end()
{
return iterator(nullptr);
}
RBtree()
:_root(nullptr)
{}
void Destory(node*root)
{
if(root==nullptr)
{
return ;
}
Destory(root->_left);
Destory(root->_right);
delete root;
}
~RBtree()
{
Destory(_root);
_root=nullptr;
}
//拷贝构造
// RBtree(const RBtree & RB)
// {
// _root=_copy(RB._root);
// }
// RBtree& operator=(RBtree t)
// {
// swap(_root,t._root);
// return *this;
// }
node*find(const K&key)
{
//使用仿函数拿出传过来参数的值
//高级泛型编程
KeyOfT kot;
node*cur=_root;
while(cur)
{
if(kot(cur->_data)_right;
}
else if(kot(cur->_data)>key)
{
cur=cur->_left;
}
else
{
return cur;
}
return nullptr;
}
}
//插入数据
pairInsert(const T& data)
{
//如果树为空
if(_root==nullptr)
{
_root=new node(data);
_root->_col=BLACK;
return make_pair(_root,true);
}
KeyOfT kot;
//树不为空
node*parent=nullptr;
node*cur=_root;
//找到节点插入的位置
while(cur)
{
if(kot(cur->_data)_right;
}
else if(kot(cur->_data)>kot(data))
{
parent=cur;
cur=cur->_left;
}
else
{
return make_pair(iterator(cur),false);
}
}
//插入数据
node*newnode=new node(data);
newnode->_col=RED;
if(kot(parent->_data)>kot(data))
{
parent->_left=newnode;
newnode->_parent=parent;
}
else
{
parent->_right=newnode;
newnode->_parent=parent;
}
cur=newnode;
//处理颜色
while(parent&&parent->_col==RED)
{
node*grandfather=parent->_parent;
//关键看叔叔
//父亲在祖父左边
if(parent==grandfather->_left)
{
//情况1,叔叔存在且为红
node*uncle=grandfather->_right;
if(uncle&&uncle->_col==RED)
{
parent->_col=uncle->_col=BLACK;
grandfather->_col=RED;
//继续往上处理
cur=grandfather;
parent=cur->_parent;
}
//情况2,叔叔不存在或者存在为黑
else
{
//叔叔不存在,单旋处理
if(cur==parent->_left)
{
RoateR(grandfather);
grandfather->_col=RED;
parent->_col=BLACK;
}
//情况三 ,叔叔存在且为黑
else
{
RoateL(parent);
RoateR(grandfather);
cur->_col=BLACK;
grandfather->_col=RED;
}
break;
}
}
//父亲在祖父右边
else
{
node*uncle=grandfather->_left;
//情况1,叔叔存在且为红
if(uncle&&uncle->_col==RED)
{
parent->_col=uncle->_col=BLACK;
grandfather->_col=RED;
//继续往上处理
cur=grandfather;
parent=cur->_parent;
}
//情况2,叔叔不存在或者叔叔为黑
else
{
//叔叔不存在
if(cur==parent->_right)
{
RoateL(grandfather);
parent->_col=BLACK;
grandfather->_col=RED;
}
//叔叔为黑
else
{
RoateR(parent);
RoateL(grandfather);
grandfather->_col=RED;
cur->_col=BLACK;
}
break;
}
}
}
_root->_col=BLACK;
return make_pair(iterator(newnode),true);
}
//右旋
void RoateR(node*parent)
{
node*subL=parent->_left;
node*subLR=subL->_right;
//链接
parent->_left=subLR;
if(subLR)
{
subLR->_parent=parent;
}
subL->_right=parent;
//判断parent是否为根
node*parentparent=parent->_parent;
parent->_parent=subL;
if(parent==_root)
{
_root=subL;
subL->_parent=nullptr;
}
//不是根处理
else
{
if(parentparent->_left==parent)
parentparent->_left=subL;
else
parentparent->_right=subL;
subL->_parent=parentparent;
}
}
void RoateL(node*parent)
{
node*subR=parent->_right;
node*subRL=subR->_left;
parent->_right=subRL;
if(subRL)
{
subRL->_parent=parent;
}
//判断parent是否为根
subR->_left=parent;
node*parentparent=parent->_parent;
parent->_parent=subR;
if(_root==parent)
{
_root=subR;
subR->_parent=nullptr;
}
else
{
if(parentparent->_left==parent)
{
parentparent->_left=subR;
}
else
{
parentparent->_right=subR;
}
subR->_parent=parentparent;
}
}
bool _isBlanceTree(node*root,int blacknum,int count)
{
if(root==nullptr)
{
if(blacknum!=count)
{
cout<<"黑色节点数量不相等"<_col==RED&&root->_parent->_col==RED)
{
cout<<"存在连续的红色节点"<_col==BLACK)
{
count++;
}
return _isBlanceTree(root->_left,blacknum,count)&&_isBlanceTree(root->_right,blacknum,count);
}
bool isBlanceTree()
{
if(_root==nullptr)
{
return true;
}
if(_root->_col==RED)
{
cout<<"根节点是红色的"<_col==BLACK)
{
blacknum++;
}
left=left->_left;
}
int count=0;
return _isBlanceTree(_root,blacknum,count);
}
// void _inorder(node*root)
// {
// if(root==nullptr)
// {
// return ;
// }
// _inorder(root->_left);
// cout<_kv.first<<":"<_kv.second<_right);
//
// }
// void inorder()
// {
// _inorder(_root);
// }
private:
node*_root;
// node*_copy(node*root)
// {
// if(root==nullptr)
// {
// return nullptr;
// }
// node* copynode=new node(root->_kv);
// copynode->_left=_copy(root->_left);
// copynode->_right=_copy(root->_right);
// return copynode;
// }
}; 2,map.h
#include"RB_tree.h"
namespace Etta
{
template
class map
{
//仿函数,拿出传过去参数的值
struct mapKeyOfT
{
const K& operator()(const pair& kv)
{
return kv.first;
}
};
public:
//在对象实例化以后,再去构造迭代器
typedef typename RBtree,mapKeyOfT>::iterator iterator;
typedef typename RBtree,mapKeyOfT>::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
bool insert(const pair& kv)
{
_t.Insert(kv);
return true;
}
private:
RBtree,mapKeyOfT> _t;
};
} 3,set.h
#include"RB_tree.h"
namespace Etta
{
template
class set
{
//仿函数,提取节点存取的值
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBtree::iterator iterator;
//实例化参数以后再去实例化迭代器
typedef typename RBtree::reverse_iterator reverse_iterator;
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
bool insert(const K& k)
{
_t.Insert(k);
return true;
}
private:
RBtree _t;
};
} 4,Iterator.h
template
struct ReverseIterator
{
//红黑树中实例化以后再实例化反向迭代器
typedef typename Iterator::reference Ref;
typedef typename Iterator::pointer Ptr;
typedef ReverseIterator Self;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{}
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
bool operator!=(const Self& s) const
{
return _it != s._it;
}
bool operator==(const Self& s) const
{
return _it == s._it;
}
};