蓝桥杯 基础练习 BASIC-18 矩形面积交

试题 基础练习 基础练习 矩形面积交

资源限制
时间限制：1.0s 内存限制：512.0MB

问题描述
平面上有两个矩形，它们的边平行于直角坐标系的X轴或Y轴。对于每个矩形，我们给出它的一对相对顶点的坐标，请你编程算出两个矩形的交的面积。

输入格式
输入仅包含两行，每行描述一个矩形。
在每行中，给出矩形的一对相对顶点的坐标，每个点的坐标都用两个绝对值不超过10^7的实数表示。

输出格式
输出仅包含一个实数，为交的面积，保留到小数后两位。

样例输入
1 1 3 3
2 2 4 4

样例输出
1.00

分析

已知两个矩形的对角顶点，求两矩形相交产生的矩形面积。
这里我们姑且认为给定的对角顶点均为左上-右下，那么我们便可得到下面的图像：

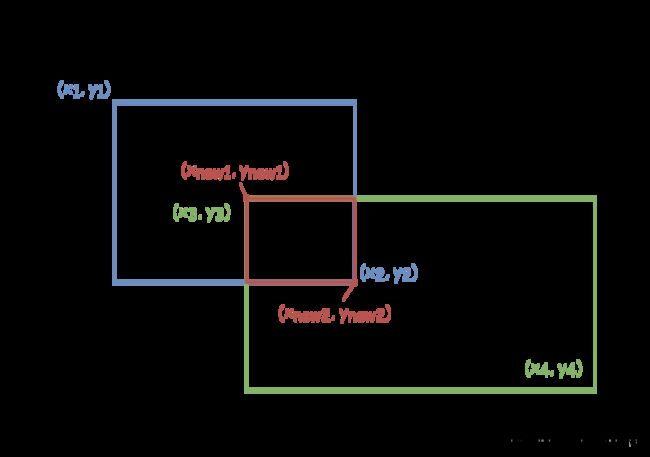
根据图像我们可以知道，新组成的矩阵实际由四个顶点中较为靠里的两个相对顶点组成，那么如何求得较为靠里的两个顶点呢？

这里我们把两个顶点$(x_{new1},y_{new1})$，$(x_{new2},y_{new2})$所划分的红色区域看作为四条直线所划分的区域，这四条直线分别为：

$$\begin{gathered} x=x_{new1} \\ x=x_{new2} \\ y=y_{new1} \\ y=y_{new2} \end{gathered}$$

这里，我们认定$x=x_{new1}$始终在$x=x_{new2}$的左边，$y=y_{new1}$始终在$y=y_{new2}$的上边
即$x_{new2}>x_{new1}$且$y_{new1}>y_{new2}$

所以接下来便是需要求这四条直线，以$x=x_{new1}$为例：

由于我们并不知道两个矩形的相对位置到底如何，但可以明确的一点是$x=x_{new1}$是在靠左的一边，所以求$x=x_{new1}$这条直线，我们要先求出两个矩形中靠左的一边，即$min(x_1,x_2)$和$min(x_3,x_4)$，然后在求得两者的最大值，这里给出公式：
$$x_{new1}=max(min(x_1,x_2),min(x_3,x_4))$$
同理，可求得其他直线：
$$\begin{gathered} x_{new2}=min(max(x_1,x_2),max(x_3,x_4)) \\ {y}_{new1}=min(max(y_1,y_2),max(y_3,y_4)) \\ {y}_{new2}=max(min(y_1,y_2),min(y_3,y_4)) \end{gathered}$$

这里要注意一点：只有当$x_{new2}>x_{new1}$且$y_{new1}>y_{new2}$时，矩阵才存在

然后根据四条直线，我们便可以计算矩阵的面积：
$$S=(x_{new2}-x_{new1})\times (y_{new1}-y_{new2})$$

Python 代码

x1, y1, x2, y2 = map(float, input().split())
x3, y3, x4, y4 = map(float, input().split())

new_x1 = max(min(x1, x2), min(x3, x4))
new_y1 = min(max(y1, y2), max(y3, y4))
new_x2 = min(max(x1, x2), max(x3, x4))
new_y2 = max(min(y1, y2), min(y3, y4))

if new_x2 > new_x1 and new_y1 > new_y2:
    print("%.2f" % ((new_x2 - new_x1) * (new_y1 - new_y2)))
else:
    print('0.00')

C/C++ 代码

#include

#define max(x, y) ((x)>(y)?(x):(y))
#define min(x, y) ((x)<(y)?(x):(y))

int main() {
    double x1, y1, x2, y2;
    double x3, y3, x4, y4;
    double new_x1, new_y1;
    double new_x2, new_y2;
    scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
    scanf("%lf%lf%lf%lf", &x3, &y3, &x4, &y4);
    new_x1 = max(min(x1, x2), min(x3, x4));
    new_y2 = max(min(y1, y2), min(y3, y4));
    new_x2 = min(max(x1, x2), max(x3, x4));
    new_y1 = min(max(y1, y2), max(y3, y4));
    if (new_x2 > new_x1 && new_y1 > new_y2)
        printf("%.2f", (new_x2 - new_x1) * (new_y1 - new_y2));
    else
        printf("0.00");
    return 0;
}