牛客网算法八股刷题系列(六)正则化与偏差、方差的联系
牛客网算法八股刷题系列——正则化与偏差、方差的联系
- 题目描述
- 正确答案: C \mathcal C C
- 题目解析
-
- 场景构建
- λ ⇔ Bias \lambda \Leftrightarrow \text{Bias} λ⇔Bias
-
- 拉格朗日乘数法角度
- 权重衰减角度(包含 λ ⇔ Variance \lambda \Leftrightarrow \text{Variance} λ⇔Variance解释)
题目描述
假如使用一个较复杂的脊回归( Ridge Regreesion \text{Ridge Regreesion} Ridge Regreesion)模型来拟合样本数据时,通过调整正则化参数 λ \lambda λ,来调整模型复杂度。当 λ \lambda λ较大时,关于偏差 ( Bias ) (\text{Bias}) (Bias)和方差( Variance \text{Variance} Variance),下列说法正确的是 ? ( ) ?(\quad) ?()
A \mathcal A \quad A当 λ \lambda λ增大时,偏差减小,方差减小;
B \mathcal B \quad B当 λ \lambda λ增大时,偏差减小,方差增大;
C \mathcal C \quad C当 λ \lambda λ增大时,偏差增大,方差减小;
D \mathcal D \quad D当 λ \lambda λ增大时,偏差增大,方差增大;
正确答案: C \mathcal C C
题目解析
观察题目,该任务是一个回归任务,并且使用基于 L 2 L_2 L2正则化的岭回归/脊回归来拟合样本数据。并对正则化项参数 λ \lambda λ与拟合偏差/方差之间的关联关系进行描述。
场景构建
已知训练集合 D t r a i n = { ( x ( i ) , Y ( i ) ) } i = 1 N \mathcal D_{train} = \{(x^{(i)},\mathcal Y^{(i)})\}_{i=1}^N Dtrain={(x(i),Y(i))}i=1N,使用的损失函数是均方误差;对应的正则化项是 L 2 L_2 L2正则化:
J ( W ) = 1 N ∑ i = 1 N ( Y p r e d ( i ) − Y ( i ) ) 2 + λ ∣ ∣ W ∣ ∣ 2 \mathcal J(\mathcal W) = \frac{1}{N}\sum_{i=1}^N (\mathcal Y_{pred}^{(i)} - \mathcal Y^{(i)})^2 + \lambda||\mathcal W||_2 J(W)=N1i=1∑N(Ypred(i)−Y(i))2+λ∣∣W∣∣2
λ ⇔ Bias \lambda \Leftrightarrow \text{Bias} λ⇔Bias
下面从两种角度来描述 λ \lambda λ与偏差之间的关系:拉格朗日乘数法角度、权重衰减角度。
拉格朗日乘数法角度
详细过程可参考:
- 机器学习笔记之正则化——拉格朗日乘数法角度
- 机器学习笔记之正则化——权重衰减角度[偏差方向]回顾部分。
在未加正则化项之前,我们只有一种途径来判别权重 W \mathcal W W在训练过程中的情况——损失函数。损失函数达到较小时,或者说损失函数减小的速度非常缓慢的时候,我们认为模型已经达到拟合。
但训练开始之前,我们对于权重的初始化 W i n i t \mathcal W_{init} Winit可以是权重空间中的任意一点。实际上,每一个初始化点都存在自己的拟合路径。这会导致:可能存在若干个损失函数结果相似,但都很小的权重结果。也就是说,使模型达到拟合对应的权重不唯一。
一种朴素想法:利用范数为代表的正则化去约束权重空间,没有落在正则化范围的权重点都被视作无效。就以题中的 L 2 L_2 L2正则化为例,它在权重空间内的形状是一个圆(不同维度存在不同形状。球、超球体等等),假设该正则化范围的半径为 C \mathcal C C,对应的优化问题描述表示如下:
由于 ∣ ∣ W ∣ ∣ 2 ||\mathcal W||_2 ∣∣W∣∣2表示权重空间中某点 W \mathcal W W到权重空间原点距离; ∣ ∣ W ∣ ∣ 2 − C ≤ 0 ||\mathcal W||_2 - \mathcal C \leq 0 ∣∣W∣∣2−C≤0意味着 W \mathcal W W不会超出 L 2 L_2 L2正则化的约束空间。
{ min J ( W ) s . t . ∣ ∣ W ∣ ∣ 2 − C ≤ 0 \begin{cases} \min \mathcal J(\mathcal W) \\ s.t. \quad ||\mathcal W||_2 - \mathcal C \leq 0 \end{cases} {minJ(W)s.t.∣∣W∣∣2−C≤0
使用拉格朗日乘数法,可以将上式转化为如下形式:
L ( W , λ ) = J ( W ) + λ ( ∣ ∣ W ∣ ∣ 2 − C ) ⇒ { min W max λ L ( W , λ ) s . t . λ ≥ 0 \begin{aligned} \mathcal L(\mathcal W,\lambda) & = \mathcal J(\mathcal W) + \lambda (||\mathcal W||_2 - \mathcal C) \\ & \Rightarrow \begin{cases} \mathop{\min}\limits_{\mathcal W} \mathop{\max}\limits_{\lambda} \mathcal L(\mathcal W,\lambda) \\ s.t. \quad \lambda \geq 0 \end{cases} \end{aligned} L(W,λ)=J(W)+λ(∣∣W∣∣2−C)⇒{WminλmaxL(W,λ)s.t.λ≥0
将目标函数展开,观察展开后的结果:
L ( W , λ ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 − λ ⋅ C \mathcal L(\mathcal W,\lambda) = \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 - \lambda \cdot \mathcal C L(W,λ)=J(W)+λ∣∣W∣∣2−λ⋅C
由于 λ , C \lambda,\mathcal C λ,C均是常数,这意味着 λ ⋅ C \lambda \cdot \mathcal C λ⋅C并不对 W \mathcal W W的更新产生影响,因而在迭代求解 W \mathcal W W的过程中可省略。也就是我们常见到的正则化的表示形式:
L ( W , λ ) = J ( W ) + λ ∣ ∣ W ∣ ∣ 2 \mathcal L(\mathcal W,\lambda) = \mathcal J(\mathcal W) + \lambda ||\mathcal W||_2 L(W,λ)=J(W)+λ∣∣W∣∣2
但并不是说 λ ⋅ C \lambda \cdot \mathcal C λ⋅C没有用处 ! ! ! 该部分的作用是每次迭代过程中调节梯度向量的大小,使其与每次迭代的梯度下降部分大小相等、方向相反。
由于这个作用,使得每次迭代过程产生梯度向量的条件下, λ \lambda λ和 C \mathcal C C的乘积被约束在了固定的范围——与本次迭代梯度向量大小相关的一个范围:
由于 C \mathcal C C是一个长度,因而 C ≥ 0 \mathcal C \geq 0 C≥0;并且 λ \lambda λ是约束条件中给定的 λ ≥ 0 \lambda \geq 0 λ≥0,因此它们两个都是非负数。
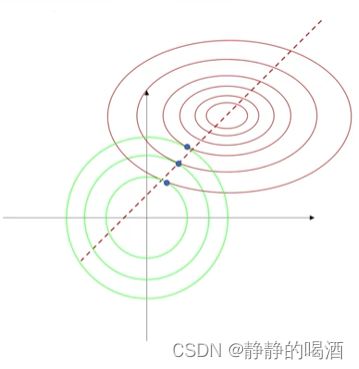
当 λ \lambda λ增大时,这意味着 C \mathcal C C不大/减小(乘积被约束), C \mathcal C C小意味着正则化范围小,导致该范围与 J ( W ) \mathcal J(\mathcal W) J(W)的最优解的距离较远,预测的结果自然不准确(偏差较大):
其中绿色圆表示正则化范围;红色线表示J ( W ) \mathcal J(\mathcal W) J(W)函数的等高线,圈越小,对应的圈内的W \mathcal W W越准确。在正则化位置不动的条件下(权重空间原点)绿色圈越小,圈内的最优解离J ( W ) \mathcal J(\mathcal W) J(W)越远,准确性自然越来越差,偏差自然也越来越大。
权重衰减角度(包含 λ ⇔ Variance \lambda \Leftrightarrow \text{Variance} λ⇔Variance解释)
详细过程可参考:
机器笔记之正则化——权重衰减角度[直观现象]
我们比较执行/未执行正则化后 W \mathcal W W更新的变化:
{ W ⇐ W − η ⋅ ∇ W J ( W ) W ⇐ ( 1 − η ⋅ α ) W − η ⋅ ∇ W J ( W ) \begin{cases} \mathcal W \Leftarrow \mathcal W - \eta \cdot \nabla_{\mathcal W} \mathcal J(\mathcal W) \\ \mathcal W \Leftarrow (1 - \eta \cdot \alpha) \mathcal W - \eta \cdot \nabla_{\mathcal W}\mathcal J(\mathcal W) \end{cases} {W⇐W−η⋅∇WJ(W)W⇐(1−η⋅α)W−η⋅∇WJ(W)
λ \lambda λ与 α \alpha α之间关联关系的推导过程表示如下:
这里以取包含正则化项损失函数 J ^ ( W ) \hat {\mathcal J}(\mathcal W) J^(W)最小值为例,其中 J ( W ) \mathcal J(\mathcal W) J(W)表示未加正则化项的损失函数。
{ W ^ = arg min W J ^ ( W ) J ^ ( W ) = J ( W ) + λ ( ∣ ∣ W ∣ ∣ 2 − C ) \begin{cases} \hat {\mathcal W} = \mathop{\arg\min}\limits_{\mathcal W} \hat {\mathcal J}(\mathcal W) \\ \hat {\mathcal J}(\mathcal W) = \mathcal J(\mathcal W) + \lambda (||\mathcal W||_2 - \mathcal C) \end{cases} ⎩ ⎨ ⎧W^=WargminJ^(W)J^(W)=J(W)+λ(∣∣W∣∣2−C)
- 由于是观察 W \mathcal W W的最值问题,下面与 W \mathcal W W无关的项忽略掉:
J ^ ( W ) = J ( W ) + λ ⋅ W T W − λ ⋅ C ⏟ W 无关 = J ( W ) + λ W T W ⋅ W T W \begin{aligned} \hat {\mathcal J}(\mathcal W) & = \mathcal J(\mathcal W) + \lambda \cdot \sqrt{\mathcal W^T\mathcal W} - \underbrace{\lambda \cdot \mathcal C}_{\mathcal W无关} \\ & = \mathcal J(\mathcal W) + \frac{\lambda}{\sqrt{\mathcal W^T\mathcal W}} \cdot \mathcal W^T\mathcal W \end{aligned} J^(W)=J(W)+λ⋅WTW−W无关 λ⋅C=J(W)+WTWλ⋅WTW - 这里令 α = 2 λ W T W \begin{aligned}\alpha = \frac{2\lambda}{\sqrt{\mathcal W^T\mathcal W}}\end{aligned} α=WTW2λ,上式可表示为如下形式:
系数1 2 \frac{1}{2} 21为求导方便使用,无实际意义。
J ^ ( W ) = J ( W ) + α 2 W T W \hat {\mathcal J}(\mathcal W) = \mathcal J(\mathcal W) + \frac{\alpha}{2} \mathcal W^T\mathcal W J^(W)=J(W)+2αWTW
由于 2 W T W > 0 \begin{aligned}\frac{2}{\sqrt{\mathcal W^T\mathcal W}} > 0\end{aligned} WTW2>0恒成立,这意味着 λ \lambda λ和 α \alpha α之间是正相关的关系。即: λ \lambda λ越大, α \alpha α越大。再次回顾上面的权重衰减过程, α \alpha α越大,意味着每次迭代过程中, ( 1 − η ⋅ α ) W ⇒ W (1 - \eta \cdot \alpha)\mathcal W \Rightarrow \mathcal W (1−η⋅α)W⇒W减小得越快。
如果将模型对样本的拟合结果视作一个复杂函数 f ( x ) f(x) f(x),可以将该函数使用泰勒公式进行表示:
f ( x ) = f ( a 0 ) + 1 1 ! f ′ ( a 0 ) ( x − a 0 ) + 1 2 ! f ′ ′ ( a 0 ) ( x − a 0 ) 2 + ⋯ + 1 n ! f ( n ) ( a 0 ) ( x − a 0 ) n f(x) = f(a_0) + \frac{1}{1!} f'(a_0)(x - a_0) + \frac{1}{2!} f''(a_0)(x - a_0)^2 + \cdots + \frac{1}{n!} f^{(n)}(a_0)(x - a_0)^n f(x)=f(a0)+1!1f′(a0)(x−a0)+2!1f′′(a0)(x−a0)2+⋯+n!1f(n)(a0)(x−a0)n
从泰勒展开式可以看出:高次项的系数越大,这个函数越复杂。对应各次项含变量的系数表示如下:
f ( a 0 ) , f ′ ( a 0 ) , f ′ ′ ( a 0 ) , ⋯ , f ( n ) ( a 0 ) f(a_0),f'(a_0),f''(a_0),\cdots,f^{(n)}(a_0) f(a0),f′(a0),f′′(a0),⋯,f(n)(a0)
由于 a 0 a_0 a0是一个常数,在 a 0 a_0 a0给定的条件下,无论这些系数是什么结构,它们必然都是关于权重 W \mathcal W W的函数。当 W \mathcal W W减小时,各次项的系数就会减小,从而使函数 f ( x ) f(x) f(x)更简单。
而简单的函数会发生欠拟合( Underfitting \text{Underfitting} Underfitting)。直观的理解是:在预测/验证的过程中,即便是样本特征相差较大的样本点,在欠拟合模型的预测结果中可能相差较小。 这意味着:
- 关于样本特征的预测结果不准确 ⇒ \Rightarrow ⇒ 偏差较大;
- 相差较大的样本点预测结果差距小 ⇒ \Rightarrow ⇒ 方差较小;
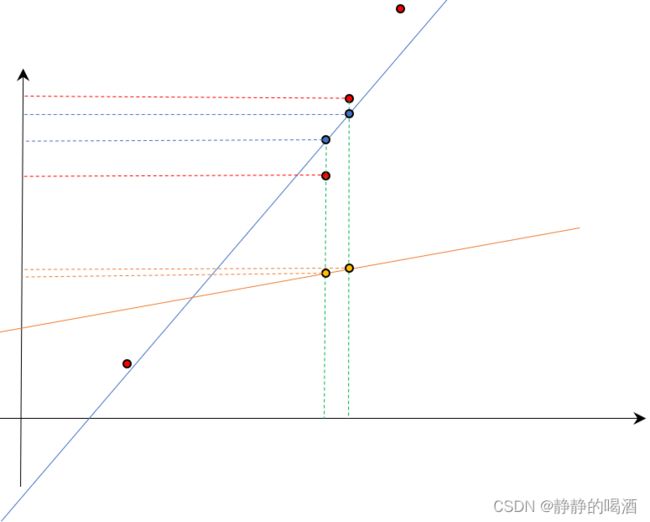
其中红色点表示样本点;蓝色线表示拟合优秀的模型结果;橙色线表示欠拟合的模型结果。取两个样本点为例。
两个红色点对应的两个模型结果分别用对应橙色点、蓝色点表示。观察:
- 红色点的纵坐标与对应蓝色、橙色点的纵坐标相比,蓝色点与红色点更接近,偏差更小;而黄色点的偏差更大;
- 比较两个黄色点坐标之间的差距,与对应的蓝色点比较,两个黄色点之间的差距更小,但是对应真实样本中的两个红色点之间的坐标差距明显更大于黄色点。这意味着:红色样本之间的特征差距,相比于蓝色线,橙色线划分得更不明显。这意味着方差更小。