【树】你真的会二叉树了嘛？ --二叉树LeetCode专题

 

Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

个人主页：主页链接

算法专栏：专栏链接

     我会一直往里填充内容哒！

LeetCode专栏：专栏链接 

    目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

代码仓库：Gitee链接

点击关注=收获更多优质内容

本章记录下目前刷到的二叉树的各类题型，做一个总结。一起来学习吧！

对二叉树还不熟悉的同学,可以看看我之前发的关于二叉树的文章哦 二叉树专题

话不多说 开始吧!

目录

题目:144. 二叉树的前序遍历

题解:

代码实现:

题目:222. 完全二叉树的节点个数

题解:

代码实现:

题目:剑指 Offer 28. 对称的二叉树

题解:

代码实现:

题目:226.翻转二叉树

题解:

代码实现:

题目:104. 二叉树的最大深度

题解:

代码实现:

题目:965. 单值二叉树

 ​编辑

题解:

代码实现:

题目:100.相同的树

题解:

代码实现:

完结撒花：

 

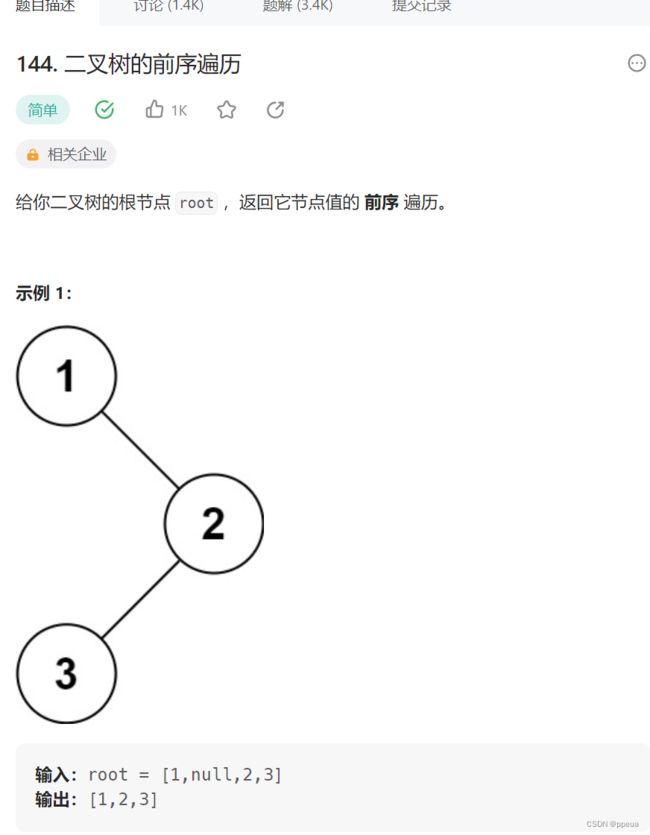
题目:144. 二叉树的前序遍历

 

题解:

先来一题简单的题目练练手,之前有提到过,二叉树的前序遍历就是通过根左右的遍历方式来进行的,所以这题总体思路也是一样.不过要说明的是,这里采用了c语言,所以输出时需要自己创建一个动态数组,每次将访问到的val存入动态数组当中即可.

(中后序大致相同,改变的仅为访问节点的时间,所以这里就不过多赘述)

代码实现:

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};
int checksize(struct TreeNode *root)
{
    return root==NULL?0:checksize(root->left)+checksize(root->right)+1;
}
void preorder(struct TreeNode* root,int *a,int *pi)
{
    if(root==NULL)
    {
        (*pi)++;
        return;
    }
    a[(*pi)++]=root->val;
    preorder(root, a, pi);
    preorder(root, a, pi);
    return;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize=checksize(root);
    int *a=(int *)malloc(sizeof(int)* *returnSize);
    preorder(root,a,0);
    return a;
}

题目:222. 完全二叉树的节点个数

题解:

这题虽然被标注为了中等题,但我认为知道二叉树的本质之后,其充其量为一个简单题,并且有秒杀的方法

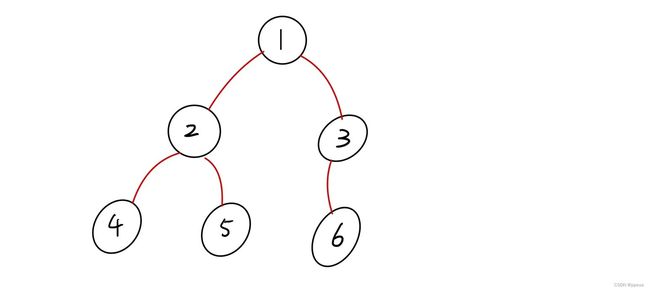
依照样例,这棵树应该长这样

 

我们要做的就是统计其本身节点数与其左右树的节点数

例如2要返回给上一层的就是3(左节点一个,右节点一个,加上自己)

而4这个节点要返回给上层的就是1(左节点无 右节点无 仅有一个自己)

所以很容易看出来 若有节点则返回1+左右子树.若无节点则直接返回0

 这样一层层递归后,1节点收到的就是其左右子树的和,最后返回给答案的就是1+左右子树和

这里给出两种代码,第一种是将每一步分开来了,若这层为空 则size不变,若不为空,则size++继续遍历左右子树(比较像前序遍历)

代码实现:

#include
struct TreeNode {
      int val;
      struct TreeNode *left;
      struct TreeNode *right;
 };
 
int TreeSize(struct TreeNode* root,int size)
{
	if (root == NULL)return size;
	size++;
	size=TreeSize(root->left,size);
	size=TreeSize(root->right,size);
	return size;
}
int countNodes0(struct TreeNode* root){
    return TreeSize(root,0);
}
//
int countNodes(struct TreeNode* root){
    return root==NULL?0:countNodes(root->left)+countNodes(root->right)+1;
}

题目:剑指 Offer 28. 对称的二叉树

题解:

镜像对称无非就是判断,其延中线对折这棵树,能否重叠.也就是根的左右子树是否完全相同

先分情况来讨论:

若两个节点都为空,则肯定相同 也就是p==NULL&&q==NULL

其中一个为空另一个不为空,则肯定不同 p==NULL||q==NULL

之后再判断两个节点的val是否相等,若相等则true,否则返回false p->val==q->val

以单个节点的视角来看,情况只有这么多,之后我们就可以开始进入递归来判断了,分别访问其左右子树,我们需要的只是知道他最后返回的是true还是false,因为单个节点的情况都被我们判断完了

每一个节点都可以看为单个节点

代码实现:

bool check(struct TreeNode* p,struct TreeNode* q)
{
    if(p==NULL&&q==NULL)return true;
    if(p==NULL||q==NULL)return false;
    if(p->val!=q->val)return false;
    return check(p->left,q->right)&&check(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root){

    return check(root->left,root->right);
}

题目:226.翻转二叉树

题解:

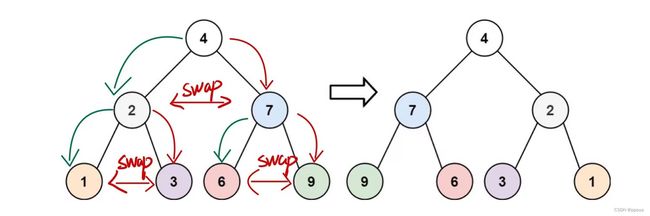
依旧从一个节点的角度来看,假设只有一个这样的二叉树,我们要做的就是

将其左右子树进行调换即可.也就是找到其左子树与右子树.拿一个中间变量,进行交换(类似两数调换)

现在我们要做的是考虑一下递归停止的情况,老样子 若根为NULL,则返回空,若不是则返回其根节点.(根节点此时为已经交换完的子树 之后再将两个根节点进行调换即可达到镜像) 

代码实现:

#include
using namespace std;
struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
 };
 class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==NULL)return NULL;
        TreeNode* left=mirrorTree(root->left);
        TreeNode* right=mirrorTree(root->right);
        root->left=right;
        root->right=left;
        return root;
    }
};

题目:104. 二叉树的最大深度

题解:

这题和节点个数的那题有点类似,不过其多了一个属性,要取最大值.

依旧先设定返回的规则,若为空则返回0.

之后遍历左子树的深度.再遍历右子树的深度,返回其最大值+1即可

这里虽然也可以秒杀,但是没有必要了,让人能看懂的代码才是一段好的代码.

代码实现:

int maxDepth(struct TreeNode* root){
    if(root==NULL)return 0;
    int left=maxDepth(root->left);
    int right=maxDepth(root->right);
    return left>right?left+1:right+1;
}

题目:965. 单值二叉树

 

题解:

这题也很简单,先判断该节点是否为空,若为空则肯定是单值,返回true

之后与其左右节点作比较,若不同则返回false

代码实现:

bool isUnivalTree(struct TreeNode* root){
    if(root==NULL)return true;
    if(root->left&&root->left->val!=root->val)return false;
    if(root->right&&root->right->val!=root->val)return false;

    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

题目:100.相同的树

 

题解:

依旧先处理初始情况(与镜像大致相同,仅遍历顺序不同)

若两个节点都为空,则肯定相同 也就是p==NULL&&q==NULL

其中一个为空另一个不为空,则肯定不同 p==NULL||q==NULL

之后再判断两个节点的val是否相等,若相等则true,否则返回false p->val==q->val

之后在遍历其左右子树即可

代码实现:

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)return true;
    if(p==NULL||q==NULL)return false;
    if(p->val!=q->val)return false;

    return (isSameTree(p->left,q->left)&&isSameTree(p->right,q->right));

}

完结撒花：

本篇博客的内容【】已经结束。

若对你有些许帮助，可以点赞、关注、评论支持下博主，你的支持将是我前进路上最大的动力。

若以上内容有任何问题，欢迎在评论区指出。若对以上内容有任何不解，都可私信评论询问。

诸君，山顶见！