随想录Day1--704二分查找,27移除元素
今天是跟卡哥学习算法的第一天,我也不知道到底能坚持到什么时候,只能说路漫漫其修远兮,吾将上下而求索!
卡哥的第一道题是力扣704,二分查找,具体题目如下:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入:nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4示例 2:
输入:nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
看到题目的第一反应,我想采用二分法进行解题,毕竟题目都明示你解决方向了。但很久没写二分法,虽然明白其中的原理,但手撕仍旧困难,所以我先用力暴力法来解决。
暴力法:
class Solution {
public int search(int[] nums, int target) {
for(int i=0 ; i < nums.length; i++){
if(nums [i] == target){
return i;
}
}
return -1;
}
因为数组中元素不重复,所以我就遍历整个数组,寻找是否有元素和目标值target相同,如果不相同,则退出for循环,返回-1;如果找到,直接return i,这里的i就是数组的下标号。
注:在java中,return表示退出当前方法,出现return后,后续全部不执行,如果在main函数return,会直接结束程序。在这里return,表示直接退出当前函数。
后面尝试写二分法,虽然写出来了,但是代码很冗余,不美观(主要在于思路没定型,整个代码补来补去的)。看了官解后,尝试着又敲了一遍,这次可以了。
二分法:
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left <= right){
int mid = (right - left) / 2 + left;
if(nums[mid] == target){
return mid;
}else if(nums[mid] > target){
right = mid - 1;
}else{
left = mid + 1;
}
}
return -1;
}
}
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
二分法第一种写法
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
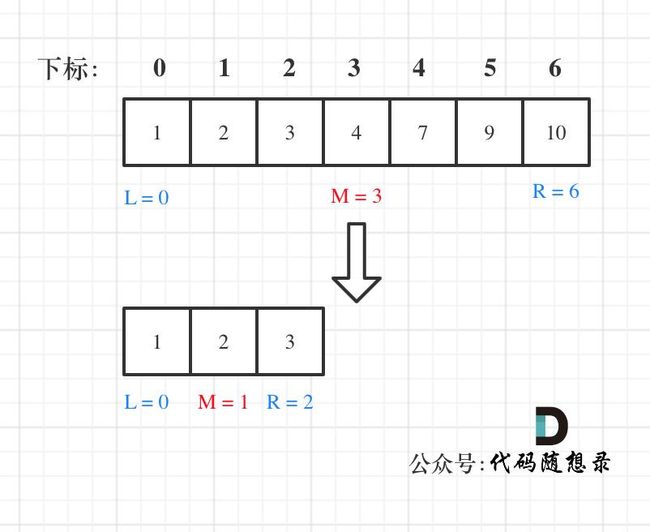
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
class Solution {
public int search(int[] nums, int target) {
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);// 防止溢出 等同于(left + right)/2
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid - 1;
}
return -1;
}
}
二分法第二种写法
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + ((right - left) >> 1);// 防止溢出 等同于(left + right)/2
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid;
}
return -1;
}
}
第二道题是力扣27题移除元素。
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
看到题目的第一反应是新建一个数组,采用遍历的方法,找到满足条件的元素放入新数组里面。但是题目要求不能使用新数组。我有看到输出的数组是比较短的,后续的数组不用(这里可以拿来做我们存放元素的数组),同时前面元素的顺序可以发生变化,我想到了交换数据。所以整体思路在于采用两个指针的形式,首先从右指针入手,如果右指针所指向的值不等于val,那么这个值就不能动,也就是没有对于的空间可以被拿来存放元素。然后又又检查左指针是否等于val,如果相等,那么交换左右指针的值,再重新进入循环。如果不相等,那么说明这个值不能动,左指针右移。直到左右指针相遇或者左指针大于右指针,说明遍历结束,退出循环。
当时这个思路为什么要先判断右指针的值呢,因为我担心左右指针指的值相同时,就会进入一种死循环,左右一直交换,都是同一个值,程序必然错误,所以就一直强调右指针所指的,一定是不等于val的值。
class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;
int right = nums.length - 1;
while(left <= right){
while(nums[right] == val){
right --;
if(right == -1){
return 0;
}
}
if(nums[left] == val){
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}else{
left ++;
}
}
return right + 1;
}
}
后面在看官方解法时,有了更多的感悟,我发现自己的思路其实就是官方解法的思路绕了一个弯,现在把它掰直就可以了。
官方的第一种齐头双指针法:
class Solution {
public int removeElement(int[] nums, int val) {
int n = nums.length;
int left = 0;
for (int right = 0; right < n; right++) {
if (nums[right] != val) {
nums[left] = nums[right];
left++;
}
}
return left;
}
}
也就是两个指针同时从左边出发,一个用作遍历,一个用作留下的值(不等于val)。当遍历经过不等于val的值时,这个值留下;当经过等于val值时,跳过。这时可以看到(left做留值指针,right做遍历指针),rignt永远>=left,不需要担心为遍历的值被覆盖的问题。
官方的第二种两头双指针法:
class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;
int right = nums.length;
while (left < right) {
if (nums[left] == val) {
nums[left] = nums[right - 1];
right--;
} else {
left++;
}
}
return left;
}
}
这种思路主要在于左右两个指针,左边的值如果是留值,左指针加1,如果等于val,就把右指针的值赋值到左指针上(因为这时候左指针指的地方是不要的),右指针减1.(这个思路可以看做,左边有空余位置,把最右边的值拉进来,保证整个[0,left]中的值都是留值,而[right,nums.length]都是不要的。)当左右指针相遇时,就能完成遍历。