差分隐私介绍以及拉普拉斯差分隐私实现细节
差分隐私
差分隐私通过在统计结果中加入了适量噪音以确保修改数据集中一条个体记录不会对统计结果造成显著影响,从而满足了隐私保护的要求。即便攻击者掌握了除一条数据外的全部其他的数据记录,差分隐私仍然能够防止攻击者分析出他不掌握的那条数据信息,有效避免了数据发布导致隐私泄露的问题。
差分隐私是有严格的、可量化的隐私保护模型。假设D和D’为相邻数据集,S为在随机函数A所有可能的输出,Pr为A(D1)获得某个值的概率。那么只要算法满足下面的公式则可以说此算法满足ε -差分隐私的标准。
![]()
为更好的理解差分隐私,下面对相关名词进行说明
相邻数据集
两个数据集只相差一条记录。
灵敏度
差分隐私保护可以通过在查询函数的返回值中加入噪声来实现,但是噪声的大小同样会影响数据的安全性和可用性。通常使用敏感性作为噪声量大小的参数,表示删除数据集中某一记录对查询结果造成的影响。敏感度分为全局敏感度和局部敏感度,通常情况下采用全局敏感度会加入过大的噪音,使数据失真,但若使用局部敏感度,在一定程度上就会泄露数据分布信息,这个时候就有了平滑敏感度
对于一个查询函数:,d为正整数,D为一个数据集的集合,代表的函数的灵敏度由下面公式定义:
D,D’是相邻数据集,敏感度是查询函数作用在相邻数据集中差值最大的那一个,当数据集针对全局时,Δf就是全局敏感度。当数据针对部分数据集时,Δf就是局部敏感度。
为了更好的理解差分隐私的作用,下面用一个例子来说明
例子
假设我们有一个医疗记录数据库 D1 在那里每条记录是一对 (名字, x), 其中 X 是一个布尔值表示一个人是否患有心脏病。例如:
| 姓名 | 有心脏病 |
|---|---|
| Rose | 是 |
| Eric | 否 |
| Joey | 否 |
| Phoebe | 否 |
| Chandler | 是 |
假设一个恶意用户 (通常被称为攻击者) 想知道Chandler是否有心脏病。假设他知道Chandler在数据库的哪一行。攻击者只能使用特定形式的查询Qi返回数据库中前i行中第一列 X 的部分总和。攻击者为了获取Chandler是否有心脏病的信息。只需要执行两个查询 Q5(D1)和Q4(D1),分别计算前五行和前四行的总和,然后计算两个查询的差别。在本例中Q5(D1)=3,Q4(D1)=2,差是1。攻击者在知道Chandler在第5行的情况下,就会知道他的心脏病状况是1(有心脏病)。这个例子显示了即使在没有明确查询特定个人信息的情况下, 个人信息如何被泄露。
如果我们用(Chandler,0)代替(Chandler,1)构造D2,那么这个恶意攻击者将能够通过计算每个数据集的Q5-Q4来区分D2和D1。 如果攻击者被要求通过ε -差分隐私算法接收Qi值,对于足够小的ε,则他将不能区分这两个数据集。
在上面医学数据库的例子中,如果我们认为f是函数Qi,那么,因为任意两个相邻数据集的差值是0或者1,所以函数的灵敏度就是1。
差分隐私拉普拉斯实现
Laplace 分布
Laplace分布是统计学中的概念,是一种连续的概率分布。如果随机变量的概率密度函数分布为:
那么它就是拉普拉斯分布。其中, μ 是位置参数, b 是尺度参数。画出来就是长这样:
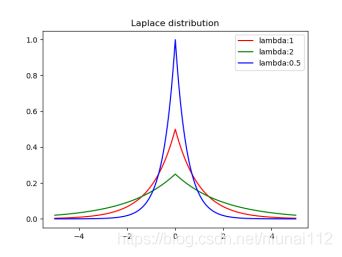
我们之前提到过,保护数据隐私的方法就是将原有的单一查询结果概率化。Laplace噪声就给我们提供了一个很好的概率化的方法。继续上面的例子,假如查询为“查询数据集中患有心脏病的人数”,并且查询结果为“2”:在传统模式下,输出就是2;在差分隐私模式下,会以比较大概率输出2左右的结果,也会以比较小的概率输出和2差别比较大的结果。但是,我们需要保证输出的期望为2(保证数据有效性)。
拉普拉斯实现DP
那么这个概率怎么用Laplace分布来实现呢?我们可以直接在输出结果2上加均值为0的噪声。直观上来说,我们通过Laplace将查询结果概率化了。然后拉普拉斯噪声就正好能满足差分隐私的要求。那么Laplace噪声是如何产生符合差分隐私的噪声的呢?我们想一下差分隐私的设计目标:当相邻数据集求结果时,两者的结果不会相差太大。那么相邻数据集在真实情况下会相差多少呢?研究这个问题是因为我们不限定用户对数据集做出什么样的查询,直观上来说,如果查询的是人数,那么相邻数据集相差不大(只会相差1),只需要加一个小一点的噪声即可造成两个结果的混淆;那如果我们查询的是人的工资呢,加一个很小的噪声显然是无法满足应用需求的(因为数据相差太大,稍微对数据的改变依然可以看出数据差别很大)。由此可见,如何设计DP机制是和查询紧密相关的。所以我们需要对查询有一个简单的了解:
因此,我们用到了上面提到的敏感度这一个概念。由于数据集中少一条记录就会对数据查询f的结果结果造成一定的影响,我们自然想知道,这个影响最大是多少呢?也就是上述定义中给出的敏感度的值Δf了。
有了 Δf 之后,我们自然想: Δf 越大,噪声应该越大, Δf 越小,噪声应该越小。这就给我们设计接下来的机制给了一定的启发。
拉普拉斯机制:给定查询函数 ,拉普拉斯机制可以表示为:
![]()
其中, Yi是独立同分布的变量,为 Lap(Δf /ε)
接下来我们将说明,上面的Laplace机制就能满足ε-DP。证明过程如下:
令b=Δf /ε
假设px表示ML(x,f,ε)的pdf(probability density function),py表示ML(x,f,ε)的pdf,则对于某个输出z,我们有:

推导过程中进行了二次缩放,第一次缩放用到了绝对值不等式进行缩放,第二个缩放用到了上面我们的定义,由此我们就可以证明拉普拉斯分布可以用来实现差分隐私。
然后我们要求拉普拉斯的概率累计函数,因为期望等于μ,而差分隐私要求期望等于0,所以直接令μ=0进行就算。
求得概率累计函数在x<μ时等于1/2exp(x/b),当x>=μ时,等于1-1/2exp(-x/b)。然后可以通过每次随机数的大小算出x的值。
当p<0.5时候,x=log(2); 当x>=0.5时,-blog(2-2p)(以此为例子,前一个同理可得);
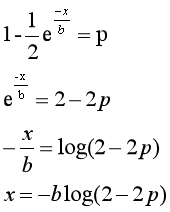
有了上面的公式,代码的实现就简单了。
噪音大小和累加和的值大小无关,只和敏感度与ε有关,因为我们只需要假如一定的噪音,让攻击者无法识别出相邻集的差值究竟是多少就行了。
假设一个医院的心脏病患者相邻集的数值分别是5000和5001,然后外界接口进行查询时,我们加入拉普拉斯噪音在返回,在分别调用接口1000次返回数据集如下。当攻击者获得某次数据的值根本不可能推导出相邻集的数据差值,也就保护了相邻集的那一条数据的隐私。

一些缺点
当攻击者能够查询足够次数接口时,攻击者能够根据查询出来的接口的频次大概反推出原始数据的值大小,因为噪声的返回是符合拉普拉斯分布的,此时攻击者也能够拿到相邻集的差值。这应该算拉普拉斯实现的一点缺点吧,但我们可以限制查询次数,或者通过加入多组ε-差分隐私来进行对抗。
差分隐私的拉普拉斯实现只能对数值型的数据发布起到保护作用,对于非数值型数据的话,拉普拉斯机制就不好处理了,此时就需要其他的实现机制来保护了,比如指数机制等。
结语
在大数据的时代中,各公司都在利用数据提供更好的服务的同时,用户隐私的保护问题也日益凸显。对用户隐私的保护既是法律的要求,也是安全行业的追求。我们相信隐私保护技术会越来越受到重视,并从学术理论迅速投入工业界实战应用。