Python学习笔记（11-2）：matplotlib绘图——图形绘制函数

文章导读
 - 课程难度：★★★☆☆
 - 重要度：★★★★★
 - 预计学习时间：2小时
 - 简介：本节主要讲解了通过matplotlib绘制各类基础图形的方法，及其对应的修饰参数等相关内容，包括：（1）基于颜色（color）、数据点标记（marker）和曲线形式（linestyle）等几个通用参数，来介绍设置参数的一些预备知识；（2）使用plot()、step()函数绘制折线图，以及三种绘制坐标对数变换图的方法；
（3）绘制散点图时设置散点颜色和大小的参数方法；（4）介绍基于基础条形图、堆叠条形图和水平堆积条形图的条形图绘制方法；（5）绘制饼图的方法及其参数的设置；（6）绘制一维和二维的直方图方法；（7）使用imshow()和pcolormesh()方法绘制热力图，并利用函数.contorf()绘制等高线；（8）绘制箱线图和小提琴图。
 - 重点涉及的函数和内容：plt.plot()、plt.step()、plt.scatter()、plt.bar()、plt.barh()、plt.pie()、plt.hist()、plt.imshow()、plt.boxplot()、plt.violinplot()。

一、设置参数的预备知识

因为部分图形绘制函数共用了一套参数体系，在颜色、曲线形状等部分的使用方式也是一致的。所以，在讲解各类图形绘制之前，我们整体性地对各类通用参数进行一个整理，并在此基础上对于颜色（color）、数据点标记（marker）和曲线形式（linestyle）等几个通用参数进行相对完整的讲解。

1、常见的绘图参数

在此，以plt.plot()函数为基础，对于一些比较重要的参数进行整理，包括线条的粗细，颜色，形状，样本点的标记，曲线标签等等。这里将各种参数分类汇总成如下几类：

（1）曲线设置参数

参数	解释
color	设置曲线颜色，形式为颜色名字（如’blue’）、十六进制色位（如’#ceb310’）或rgb三元组（如(0.3, 0.3, 1)）
drawstyle	默认default，后四种即plt.step()函数的where参数，可选{‘default’, ‘steps’, ‘steps-pre’, ‘steps-mid’, ‘steps-post’}
linestyle	设置曲线形状，可选参数包括{‘-’, ‘–’, ‘-.’, ‘:’, ‘’,’ ',‘none’}
linewidth	设置曲线宽度
alpha	设置曲线透明度，范围为0（透明）至1（不透明）

（2）数据点标记（marker）的设置参数

参数	解释
marker	marker的形状，默认为None即不输出点
markersize	marker的大小
markeredgecolor	marker边缘的颜色
markeredgewidth	marker边缘的大小
markerfacecolor	marker正中部分的颜色
markevery	指示哪些数据点会输出marker，传入的是位置列表；也可传输一个整数N，表示每N个输出一个
fillstyle	指代marker的填充形式，例如全填充、只填充上半部分等。可选参数包括{‘full’, ‘left’, ‘right’, ‘bottom’, ‘top’, ‘none’}

（3）其他参数

参数	解释
label	设定曲线的名称，在显示图例的时候会加以显示
visible	设置曲线是否可见（为False则曲线显示空白、图例保存）

2、标记点与线形：marker及linestyle

对于曲线上每一个散点，均可以利用一个标记进行单独的显示，这个标记被叫做marker。它有许多可选的参数，这里将可以直接作为参数调用的主要部分摘自官方文档整理如下：

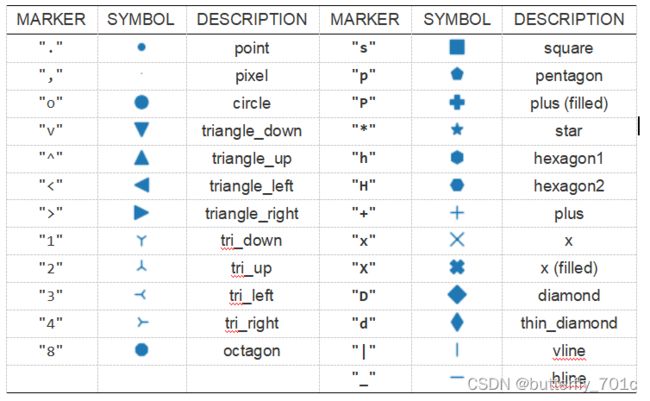
与此同时，绘制曲线时，其线型（linestyle）也有多种可选参数，整理如下：

linestyle	description
‘-’ or ‘solid’	solid line
‘–’ or ‘dashed’	dashed line
‘-.’ or ‘dashdot’	dash-dotted line
‘:’ or ‘dotted’	dotted line
‘None’	draw nothing
’ ’	draw nothing
‘’	draw nothing

作为marker和linestyle的参数，上述参数表对于所有能用上它们的函数都适用。

3、颜色与颜色序列：color与cmap

对于color，我们能传递多种参数，最常用的有三种传参的形式：

（1）颜色的名字，例如'blue'。
（2）rgb值，以一个三元组表示，例如(0.3, 0.3, 1)。
（3）16位进制的色号，例如'#ceb310'，其中ce、b3、10分别是r、g、b的值，这个值对应回十进制，实际上是在0-255中取。

我们可以通过已有的帮助文档了解常用的一批颜色的名称，以便于我们访问和选用[ 参考：官方文档1、官方文档2、官方文档3]。例如如下源于官方示例的色彩图，实际上内置的颜色名称远比下面要丰富：

但是，访问一个特定的颜色并不是本节讲解colors的全部。我们这里继续补充一个matplotlib中与颜色相关的很有意义的功能cmap，cmap即colormap。当访问一个cmap，便可访问整组颜色，并依照需要选择其中的某一个。例如在这里，我们首先观察两组不同的cmap，其各种各样的内置cmap详见各种官方文档链接：camp官方文档

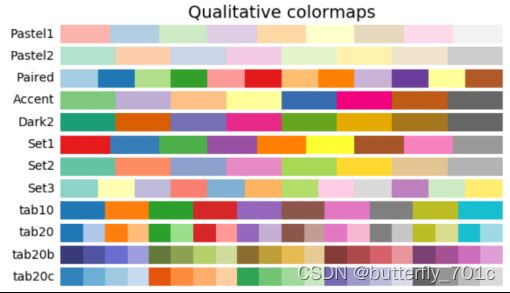
上面展示了两个cmap，这里显示的每一行就是一个cmap的颜色序列，左侧是这个cmap的名称。用系统内置的颜色序列方式是，利用plt.get_cmap()函数访问某个cmap的名称，即可访问对应的颜色序列，返回的是一个Colormap对象，当传递列表时，会得到对应的颜色数目，传递的列表有两种主要形式：

（1）正整数列表，返回的是cmap的对应位置的颜色
（2）0至1的小数列表，会乘以cmap的颜色数目N转成cmap的对应位置，接着返回cmap对应位置的颜色
返回的结果是RGBA颜色对应的数值。

先导入本节需要用到的函数包和数据表：

import matplotlib.pyplot as plt
import matplotlib
import numpy as np
import pandas as pd

trees = pd.read_csv('lesson11/trees.csv')
iris = pd.read_csv('lesson11/iris.csv')
doctorates = pd.read_csv('lesson11/doctorates.csv')

具体使用示例如下：

#访问一个cmap，顺带可以访问它的.N属性获得它的颜色数目
cmap = plt.get_cmap("Dark2")
colorseries = cmap([0, 1, 2])

cmap.N			# 获得该cmap的颜色总数
colorseries		# 获得cmap的

#在访问出cmap之中的颜色序列colorseries之后，我们用这三种颜色进行绘图：
x = np.linspace(0, 2, 20)
y1 = 2 * x -1
y2 = x 
y3 = x ** 2

plt.figure()
plt.plot(x, y1, color = colorseries[0])
plt.plot(x, y2, color = colorseries[1])
plt.plot(x, y3, color = colorseries[2])
plt.show()

输出如下：

8 
[[0.10588235 0.61960784 0.46666667 1.        ]
 [0.85098039 0.37254902 0.00784314 1.        ]
 [0.45882353 0.43921569 0.70196078 1.        ]]

cmap也可以在一些函数内作为参数，例如在plt.scatter()支持cmap参数，这个参数允许接收一个cmap标记各组元素的各自颜色。

二、折线图

先定义一些数据如下：

x = np.linspace(0, 2, 20)
y1 = 2 * x -1
y2 = x 
y3 = x ** 2

1、plot

plt.figure()

plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)

plt.show()

输出图像如下：

2、step

step图，它假定的是x一直递增，但是其中的x在x[i]到x[i + 1]之间都取同一个值，默认是y[i+1] 请参考：step图官方文档。
相比plot而言，step多了一个where参数({'pre', 'post', 'mid'}。当where为pre时，表示x在x[i]到x[i + 1]之间一直取y[i + 1]，为post时，表示一直取y[i]，为mid时，表示在x到x+1的中点跳变，where的默认值为pre。我们再一段代码展示其效果：

x = np.linspace(0, 2, 5)
y = x ** 2

plt.figure()
plt.step(x, y, label = 'pre')
plt.step(x, y, where = 'post', label = 'post')
plt.step(x, y, where = 'mid', label = 'mid') 
plt.legend()
plt.show()

输出图像如下：

3、坐标对数变换的图：plt.loglog()、plt.semilogx()和plt.semilogy()

我们首先绘制loglog函数的图。loglog是同时将x和y标度取对数后作图：

x = np.linspace(1, 100, 100)
y1 = 2 ** x
y2 = x ** 0.5
plt.figure()
plt.plot(x, y1)
plt.figure()
plt.loglog(x, y1)
plt.show()

plt.semilogy()函数和plt.semilogx()与plt.loglog()类似，是单独将y或x的值取对数后作图：

plt.figure()
plt.semilogy(x, y1)			# 对y取对数后作图
plt.figure()
plt.semilogx(x, y2)			# 对x取对数后作图
plt.show()

输出图像如下：

三、散点图：plt.scatter()

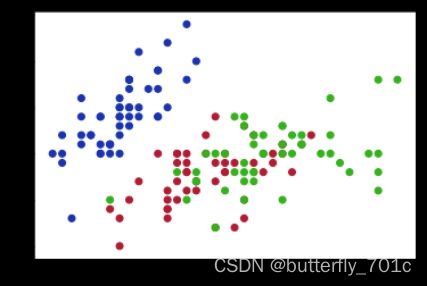
散点图利用plt.scatter()绘制，同时利用参数c根据曲线的各个点指定点的颜色，利用参数s根据设置各个散点的大小， 利用参数marker指定点的形状。在这里取鸢尾花数据集的花萼长和花萼宽进行散点图绘制：

1、颜色参数

genus列是鸢尾花数据集中的类别属性，我们用它作为我们的分组变量。我们设置一个颜色的字典，利用列表推导式制作每个点的颜色（二维列表），将它传递给函数作为参数c：

x = iris['lcalex']
y = iris['wcalex']
genus = iris['genus']

colormap = {0:[0.1, 0.2, 0.7], 1:[0.7, 0.1, 0.2], 2:[0.2, 0.7, 0.1]}
color = [colormap[i] for i in genus]

plt.figure()
plt.scatter(x, y, c = color)
plt.show()

输出图像如下：

2、散点的大小参数

利用的是参数s，它的值就是各个点的大小，我们根据trees数据的的Volume（即树在该周长和高度下的黑莓产量）设置点的大小：

x = trees['Girth']
y = trees['Height']
area = trees['Volume'] ** 1.5

plt.figure()
plt.scatter(x, y, s = area)
plt.show()

输出图像如下：

对于s参数而言，还有其扩展的功能，它可以不是传入数组，而是传入一个通过numpy建立的maskedarray。这是一个带对应布尔值的数组，它可以实现的是在值为True时输出该点，在False时不输出该点[ 其实直接在早先按照逻辑判断，将数组按照条件语句拆成多个部分分别画图也可以达到一样的效果。]。请注意通过numpy构建如下maskedarray的方式：

x = trees['Girth']
y = trees['Height']
area = trees['Volume'] ** 1.5

plt.figure()
area1 = np.ma.masked_where((np.array(x) < 14) & (np.array(y) < 77), area) 
area2 = np.ma.masked_where((np.array(x) > 14) | (np.array(y) > 77), area)
plt.scatter(x, y, s=area1, marker='^')
plt.scatter(x, y, s=area2, marker='o')
plt.show()

输出图像如下：

四、条形图：bar和barh

这里可以绘制一般的纵向的条形图，也可以绘制横向的条形图，二者分别通过两个函数名字分别为bar和barh[ 请参考：bar()函数官方文档、barh()函数官方文档]。
bar()函数常用的参数如下：

x：x轴标度的值，也是即将绘制的直方图的中心点（可以用align调节）
align：可选'center'或'edge',为edge时将柱子左边缘（而不是中心）对齐至下标
width： 一个条形图的宽度
bottom：条形图的绘制起点，在竖向的条形图中即底部的点

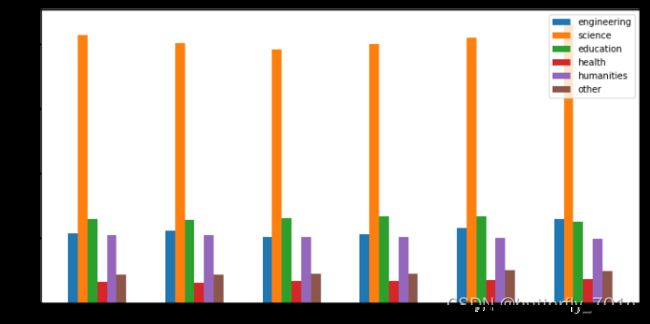
1、基础条形图

具体示例如下：

offset = 0.1
plt.figure(figsize = (12, 6))
x = doctorates['year']
y1, y2, y3  = doctorates['engineering'], doctorates['science'], doctorates['education']
y4, y5, y6 = doctorates['health'], doctorates['humanities'], doctorates['other']

# 设置最左边至最右边各个柱子的位置，其宽度固定为0.1
plt.bar(x - 2.5 * offset, y1, width = 0.1, label ='engineering')	
plt.bar(x - 1.5 * offset, y2, width = 0.1, label ='science')
plt.bar(x - 0.5 * offset, y3, width = 0.1, label ='education')
plt.bar(x + 0.5 * offset, y4, width = 0.1, label ='health')
plt.bar(x + 1.5 * offset, y5, width = 0.1, label ='humanities')
plt.bar(x + 2.5 * offset, y6, width = 0.1, label ='other')
plt.legend()											# 设置图例
plt.show()

输出图像如下：

2、堆叠条形图

参数bottom设置的是我们这个条形图的绘制起点，也就是底点，我们从这个底点向上画图，就能得到堆叠的效果
实现堆叠型柱形图的代码示例如下。请注意，为了令图形保持协调统一，最好是保持逻辑上是一组条形图中各个x或者width等参数的一致。代码及输出图像如下：

plt.figure(figsize = (12, 6))
x = doctorates['year']
y1, y2, y3  = doctorates['engineering'], doctorates['science'], doctorates['education']
y4, y5, y6 = doctorates['health'], doctorates['humanities'], doctorates['other']

# 绘制堆叠图时，需要每次设置底端为之前已绘制各列数据的加和
plt.bar(x, y1, bottom = 0, width = 0.6, label ='engineering')
plt.bar(x, y2, bottom = y1, width = 0.6, label ='science')
plt.bar(x, y3, bottom = y1 + y2, width = 0.6, label ='education')
plt.bar(x, y4, bottom = y1 + y2 + y3, width = 0.6, label ='health')
plt.bar(x, y5, bottom = y1 + y2 + y3 + y4, width = 0.6, label ='humanities')
plt.bar(x, y6, bottom = y1 + y2 + y3 + y4 + y5, width = 0.6, label ='other')
plt.legend()
plt.show()

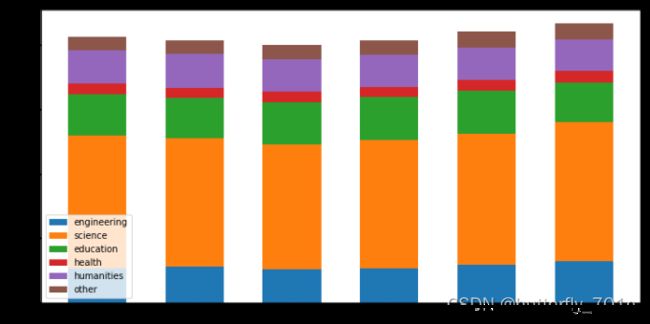
3、水平堆积条形图

上述两个重要的参数width和bottom，放到水平的条形图中的对应参数是left和height。我们在此简单地将刚刚的代码修改一下，并利用plt.barh()绘制水平方向的堆叠图：

plt.figure(figsize = (12, 6))
x = doctorates['year']
y1, y2, y3  = doctorates['engineering'], doctorates['science'], doctorates['education']
y4, y5, y6 = doctorates['health'], doctorates['humanities'], doctorates['other']

plt.barh(x, y1, left = 0, height = 0.6, label ='engineering')
plt.barh(x, y2, left = y1, height = 0.6, label ='science')
plt.barh(x, y3, left = y1 + y2, height = 0.6, label ='education')
plt.barh(x, y4, left = y1 + y2 + y3, height = 0.6, label ='health')
plt.barh(x, y5, left = y1 + y2 + y3 + y4, height = 0.6, label ='humanities')
plt.barh(x, y6, left = y1 + y2 + y3 + y4 + y5, height = 0.6, label ='other')

plt.legend()
plt.show()

输出图像如下：

五、饼图：plt.pie()

饼图能清晰地展示一组数据的分布情况。绘制饼图使用plt.pie()函数[请参考： 饼图的官方文档 ]。
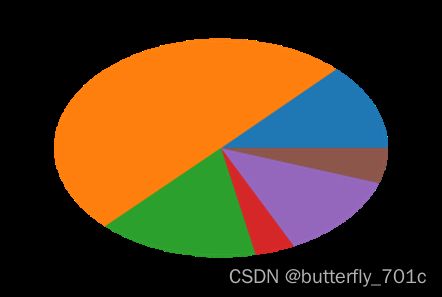
我们首先介绍其最基本的调用方式：

value2001 = doctorates.values[0][1:]
plt.figure()
plt.pie(value2001)
plt.show()

输出图片如下：

在绘制饼图的时候，有几个相对重要的参数：

1、explode，指示某个饼图中的块从圆心向外的偏出量，0为不进行偏出
2、radius，饼图绘制的大小的半径值，默认值为1
3、wedgeprops，一个指出饼图中各个块的图像属性的字典。其中需要注意width属性，指示每个块的大小的半径值。系统内，各个块从外向内绘制。其他常用的参数类似于此前接触的同名参数，调用形式相同。

这里请务必注意radius和wedgeprops中width属性的关系。这些半径值全部是绝对数字而非比例，例如半径radius为0.9的圆，遇上width为0.7时，表示在半径0.9的圆区域内，从边线向内绘制一个0.7半径的环，剩余内部半径0.2的小圆置空。这个是绘制饼图时相对有些需要仔细理解的重要内容。
除了这三个参数以及字典之外，在饼图中有许多可以利用的这些参数，包括颜色、边线、文本标记的调整等，但这些较为容易理解，因此直接在此给出一个相对复杂的饼图的例子，并在绘制这个饼图的过程中以批注逐一说明：

value2001 = doctorates.values[0][1:]
labels = ['engineering', 'science', 'education', 'health', 'humanities', 'other']
colors = ['red', 'yellow', 'blue', 'green', 'gray', 'brown']
explode = [0.1, 0, 0, 0, 0, 0]		# 设置偏移量参数列表，只有第一块进行偏移

plt.figure()
plt.pie(value2001,

		# 图形设计部分 
         explode = explode,		# 指示各个区块从圆心向外的偏移量，
							#（0为不进行偏移）
         radius = 1.2, 			# 半径值，指示饼图绘制的大小，
         labels = labels,			# 标签列表，指示每个区块的标签
         colors = colors,		# 颜色列表，指示每个区块的颜色
         shadow = True,		# 指示是否绘制阴影，默认为False
         startangle = 0, 		# 指示饼图起始的角度与x正方向的夹角，
							#（默认起始为自x正方向开始逆时针旋转）
         counterclock = False, 	# 指示饼图各个块顺时针还是逆时针旋转
        
        	# 文字标记设计部分
         autopct='%1.2f%%', 	# 设置饼图上输出百分数的形式，
							# 当不为None时，传递格式化字符串或函数名即可
         pctdistance = 0.7, 	# 设置在百分数偏离圆心的距离比例，默认0.6
         labeldistance = 1.2, 	# 设置在标签偏离圆心的距离比例，默认1.1
        
        	# 其他补充参数
         wedgeprops = {'edgecolor': 'w', 	# 边框线的颜色
                      'linewidth': 2, 	# 边框线的宽度
                      'width':0.4 		# 指示条形图的宽度（占整个圆弧的比例）
		},
)

# 如果希望为饼图显示为正圆形，可以在其后设置如下图形参数[ 请参考：https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.set_aspect.html#matplotlib.axes.Axes.set_aspect]
plt.axis('equal') 				# 'auto'为适应画布长宽比，'equal'为长宽相同
							# 给一个数值则为给定一个特定的长宽比
plt.show()

输出图像如下。请注意此时是在半径为1.2的圆形区域内，绘制一个宽度为0.4的环形。与此同时，我们利用了一个plt.axis()函数，用以指示饼图的显示形状为正圆形，即将长宽设置为等长：

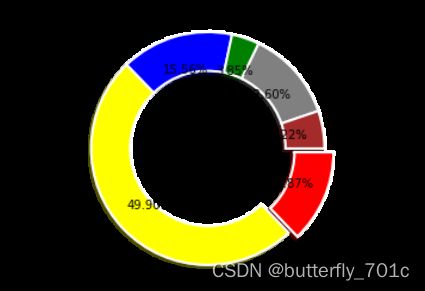
我们可以绘制数个环形的图片，将数年的数据输出在同一张饼图上，这里绘制三年的数据。这里我们就运用tab20c的cmap来获取深浅程度略有差异一组颜色，分别指示三年的分布变化（tab20c只支持20种颜色）：

# 建立每年各个领域授予学位的数目的列表
value2001 = doctorates.values[0][1:]	
value2002 = doctorates.values[1][1:]
value2003 = doctorates.values[2][1:]

# 定义标签和各个环的大小，一般而言间距和wedgeprops参数字典里的width相等
labels = ['engineering', 'science', 'education', 'health', 'humanities', 'other']

# 定义半径，r每次缩减0.2，width每次缩减0.2，就绘制了三个等宽的环
r = [1, 0.8, 0.6]

# 定义颜色序列
cmap = plt.get_cmap("tab20c")
colors01 = cmap(np.arange(6) * 4 + 0)
colors02 = cmap(np.arange(6) * 4 + 1)
colors03 = cmap(np.arange(6) * 4 + 2)

plt.figure()
plt.pie(value2001, radius = r[0],colors = colors01, \
	wedgeprops = {'edgecolor': 'w','width':0.2}, labels = labels)
plt.pie(value2002, radius = r[1],colors = colors02, \
	wedgeprops = {'edgecolor': 'w','width':0.2})
plt.pie(value2003, radius = r[2],colors = colors03, \
	wedgeprops = {'edgecolor': 'w','width':0.2})

plt.axis('equal') 
plt.show()

输出图像如下。other类全为浅灰色的原因是tab20c仅有5类共20个颜色，other超出了访问范围，因此全部取了tab20c的最后一个颜色浅灰色。不过在此，效果恰合需求：

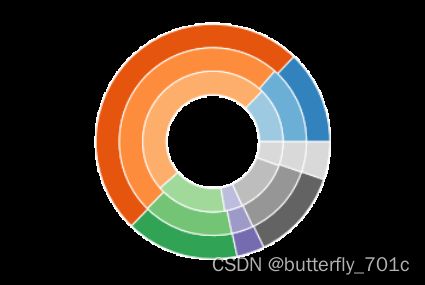
这种方式的展示在比较各种分配侧重的时候显得很直观，例如城市间第一二三产业产值占比、消费类型占比的比较等。

六、直方图

直方图用于观察一个变量分布情况，传递的是一维数据，返回的图形横坐标是值，纵坐标是频数或是分布概率。绘制直方图一般用函数plt.hist()[ 请参考：hist()函数官方文档]
plt.hist()函数有许多需要描述的参数，在此整理如下：

1、bins，指示整个图分多少个直方，默认值是10；如果是给出一个连续的数值序列，则每一个直方的区间为相邻序列值所划定的左闭右开区间（除了左右一个）。
2、range，设置绘图的区间，默认值为样本的最小值（左端）、最大值（右端）。
3、weights，样本权重，与样本等长。当weights参数设置时，直方图返回的结果不是频数而是加权的和。
4、cumulative，当为False时绘制普通直方图，为True时绘制累积频数的直方图。
5、bottom ，指示每个直方图的底点的位置，类似于条形图的bottom参数
6、align，可选'left'、'mid'、'right'，指示直方图对齐的位置，分别指示直方图的左边、中间、右边与对应值对齐
7、orientation，可选'horizontal'、'vertical'。如果为horizonal，则横着画，类似于bar和barh的关系。
8、density，如果为True，则将直方图的面积标准化为1（不是将频数除以样本数），使纵轴返回一个概率密度。

1、一维直方图：plt.hist()

我们使用随机采样构建一个正态分布的采样结果，来展示这个函数的调用方式，具体示例如下：

from scipy import stats
np.random.seed(15) 			# 令随机数固定
x = stats.norm.rvs(loc = 3, scale = 2, size = 1000) #平均值为3，标准差为2
plt.figure()
plt.hist(x,
       bins = 30, 
       range = (-5, 13),  
       weights = np.ones(1000), 
       cumulative = False, 
       bottom = 0, 
       align = 'mid',
       orientation = 'vertical', 
       color = 'blue',			# 各个分箱的颜色，和其他函数的区别不大
       density = True, 
)

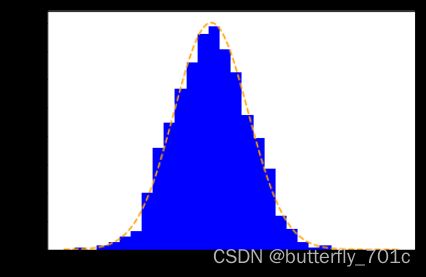
在绘图结果之上，我们也可以顺带做一个拟合分布的曲线：

oc_fit, scale_fit = stats.norm.fit(x)
plot_x = np.arange(-5, 13, 0.01)
plot_y = stats.norm.pdf(plot_x, loc = loc_fit, scale = scale_fit) 

# 根据对应的x和y绘制拟合分布的曲线
plt.plot(plot_x, plot_y, linestyle = '--', color = 'orange') 
plt.show()

输出图像如下：

2、二维直方图：plt.hist2d()

二维数据直方图[ 请参考：hist2d()函数官方文档]，二维数据的直方图用函数plt.hist2d()。绘制二维数据的直方图类似于绘制一个热力图，即颜色的从高到低代表频数，横纵坐标是二维数据本身。在这个里面有部分参数和plt.hist()之中的很相似，区别主要是分箱和区间的定义方式，以及利用cmap定义直方图的颜色展示：

np.random.seed(15) # 令随机数固定
x = stats.norm.rvs(loc = 3, scale = 2, size = 10000)
y = stats.norm.rvs(loc = 0, scale = 1, size = 10000)

figure = plt.figure()
plt.hist2d(x, y,
         bins = [30,20], 	# 与此前一样，只是变成需要传递二维数组
						# 也可以只传一个N，代表两个维度都分N个区间
         range = [[-5, 13], [-3, 3]], 	# 绘制横纵坐标的值域区间，传递二维列表
         weights = None, 			# 样本权重，此时需要传递一个二维数组
         alpha = 0.9, 				# 绘制区间的透明度
         cmap = 'coolwarm' 			# 填充直方图颜色的cmap
)
plt.legend()
plt.show()

输出图像如下：

七、热力图

热力图实际上可以说是一种用颜色来描述数值大小的分布。在绘制热力图中，最基础的是imshow，层级图pcolormesh绘制的是一个一个的方块，而contorf绘制的是平滑的过渡曲线。但热力图绘制的是各个区间点的值，这个值对应到在直方图中时，就是我们的概率密度。我们为了能够能传递数据，就首先拿着我们刚刚的x和y，来先行计算频数和每个方框的概率密度。
步骤1：定义绘制的长和宽即区间个数。接着进行数目为num的随机采样，这里仍然以正态分布的方式采集样本：

import random
random.seed(20)		# 固定随机数种子
num = 10000			# 采样数目
x_width = 30
y_width = 20 

x = stats.norm.rvs(loc = 3, scale = 2, size = num)
y = stats.norm.rvs(loc = 0, scale = 1, size = num)

步骤2：设置width和height的上下区间并直接用于构建一个等差数列，这个区间基于3delta原则计算，可调整。这里的格子中，仅保存从0.3分位数至99.7分位数；width个区间需要width + 1个元素来指示。

x_width_valuethre = np.linspace(np.percentile(x, 0.3), np.percentile(x, 99.7), x_width + 1)
y_width_valuethre = np.linspace(np.percentile(y, 0.3), np.percentile(y, 99.7), y_width + 1)

步骤3：计算某个区间的频数（pf）和累积的频数（cf）。注意的第一是传入的元组中，x的宽是列数，y的宽是行数，可能与我们的潜意识相反，这个问题贯穿程序。第二是需要用pandas DataFrame的切片修改，因为用numpy数组切片后再次切片做元素访问，不会修改原值。

z_pf = pd.DataFrame(np.zeros((y_width, x_width)))
z_cf = pd.DataFrame(np.zeros((y_width, x_width)))
for x_tmp, y_tmp in zip(x, y):
    z_pf.iloc[(y_width_valuethre[1:] > y_tmp) & (y_width_valuethre[:-1] < y_tmp),
              (x_width_valuethre[1:] > x_tmp) & (x_width_valuethre[:-1] < x_tmp),] += 1 
    z_cf.iloc[(y_width_valuethre[1:] > y_tmp),
              (x_width_valuethre[1:] > x_tmp)] += 1 

步骤4：利用累积频数除以总样本数可得累积概率分布（z_cd）。利用每一个区间的频数除以总样本数作为概率值，之后对每个区间的面积进行标准化（将总面积标准化为1），得到最终的概率密度（z_pd）：

z_pd, z_cd = z_pf.copy(), z_cf.copy()
area = np.ptp(x) * np.ptp(y)
x_thre_diff, y_thre_diff = np.diff(x_width_valuethre), np.diff(y_width_valuethre)
for i in range(x_width):
    for j in range(y_width):
        z_pd.iloc[j, i] /= (num * x_thre_diff[i] * y_thre_diff[j])
        z_cd.iloc[j, i] /= (num)
z_pd, z_cd = np.array(z_pd), np.array(z_cd)

最后，我们将这两者进行保存成为pickle文件：

import pickle

filename_z_pd = 'lesson11\\z_pd.pkl'
filename_z_cd = 'lesson11\\z_cd.pkl'

file_z_pd = open(filename_z_pd, 'wb') 
file_z_cd = open(filename_z_cd, 'wb') 

pickle.dump(z_pd, file_z_pd)
pickle.dump(z_cd, file_z_cd)

file_z_pd.close()
file_z_cd.close()

1、imshow()

我们首先将数据读取出来，这个步骤对后面的plt.pcolormesh()函数和plt.contourf()函数相同：

import pickle
filename_z_pd = 'lesson11\\z_pd.pkl'
filename_z_cd = 'lesson11\\z_cd.pkl'

file_z_pd = open(filename_z_pd, 'rb') 
file_z_cd = open(filename_z_cd, 'rb')

z_pd = pickle.load(file_z_pd)
z_cd = pickle.load(file_z_cd)

import matplotlib.pyplot as plt
plt.imshow(z_pd)

输出图像如下：

对于它，我们也有一些重要的修饰参数：

1、X，传入的数据，至少是一个二维数组，但也可以传入一个(M,N,3)或是(M,N,4)的三维数组，最后一维数组标记的是颜色（3维维RGB，4维为RGBA）。
2、cmap，待使用颜色序列cmap，用以映射数值与对应颜色。
3、aspect，类似于饼图中的plt.axis()函数，可选'equal'或'auto'。equal下，各个像素点（注意是每一个小方块）保持为正方形，即图像长宽为矩阵的长宽。
4、interpolation，颜色的插值方式，可不调整。
5、origin，指示数组的[0, 0]点是在左上方还是左下方，可选'upper'或'lower'，默认为'upper'。
6、extent，指示左、右、下、上的数值边界，原有的像素点会被压缩和拉伸。

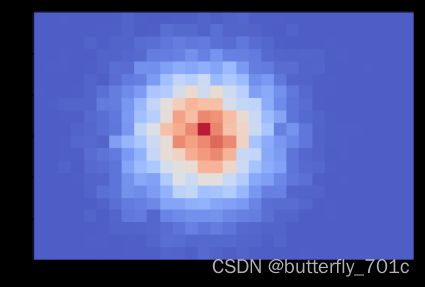
我们集中调用一个例子，进行绘图部分：

plt.figure(figsize = (8, 6))
fig = plt.gcf()
ax = plt.gca()
im = ax.imshow(z_pd,
 			cmap = plt.get_cmap('jet'), 
            	aspect = 'equal', 
			interpolation = 'nearest', 
			origin = 'lower', 
			extent = (20, 40, 5, 20), 
			alpha = 0.8 				# 图像的透明度
)

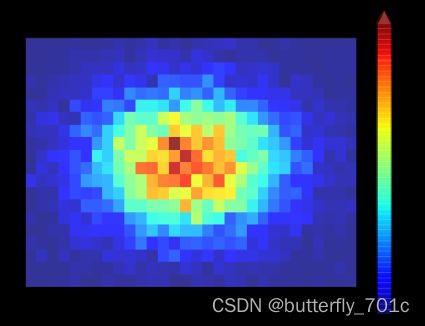
最终输出一个带颜色标尺的图形：

fig.colorbar(im, 			# 待为之绘制的图像
		  ax = ax,			# 待绘制标尺图像所属的axe对象
		  extend = 'max' 	# 指示上下是否绘制一个尖头作为顶端，
						# 可选'neither','both','min','max'
)
plt.show()

2、pcolormesh()

相比于imshow绘制时是每一个点绘制一个颜色块，在pcolormash中，每一个实际绘制的样本点，实际上是由x和y所环绕的矩形。
具体示例如下：

#准备数据
import random
from scipy import stats
random.seed(20)		# 固定随机数种子
num = 10000			# 采样数目
x_width = 30
y_width = 20 
x = stats.norm.rvs(loc = 3, scale = 2, size = num)
y = stats.norm.rvs(loc = 0, scale = 1, size = num)
x_width_valuethre = np.linspace(np.percentile(x, 0.3), np.percentile(x, 99.7), x_width + 1)
y_width_valuethre = np.linspace(np.percentile(y, 0.3), np.percentile(y, 99.7), y_width + 1)

x, y = [], []				# 构建这个区间，重新定义x和y
for ythre_tmp in y_width_valuethre:
    y.append([ythre_tmp] * (x_width + 1))  
    x.append(x_width_valuethre)
x = np.array(x)
y = np.array(y)

我们也结合上面的x、y和上述例子来调用这个函数，以观察效果。需要指出的是，x和y可以不给出，只给出z_pd这样同样能完成图像的绘制，但横纵坐标的绘制结果会与plt.imshow()函数相同，给出x、y之后横纵坐标会参考x和y进行设置：

plt.figure(figsize = (8, 6))
ax, fig = plt.gca(), plt.gcf()
im = ax.pcolormesh(x, y, z_pd, 					# x和y可以不给出
										# 届时绘制的结果和imshow一样
                cmap = plt.get_cmap('jet'), 	# cmap颜色系统
                alpha = 0.8, 				# 透明度
                edgecolors = None # 每个色块边缘的颜色，可选'none'、None、'face'、color、color sequence五种，分别指示无颜色、内置基础色、临近格子颜色或是自定义颜色（序列）
)
fig.colorbar(im, ax = ax)
plt.show()

输出图像如下：

3、.contorf()

我们可以绘制等高线图plt.contorf()和plt.contor()，其中，plt.contorf()绘制的是填充的等高线区间，plt.contor()绘制的是等高线的线本身，它的x和y也不是必须的，但如果给出x和y时，和刚刚的x和y稍有不同。
我们简单讲解一下即可，仅用其少数几个参数：

plt.figure(figsize = (8, 6))
ax, fig = plt.gca(), plt.gcf()

# 绘制等高线的填充区间
cf = ax.contourf(x[:-1, :-1], y[:-1, :-1], z_pd,
             10, 					# 指示颜色标尺分为多少格，
									# 也即等高线的填充区间有多少个
              cmap = plt.get_cmap('jet'),
              alpha = 1				# 设置不透明度
)

# 绘制等高线的线，以白色等高线颜色
ax.contour(x[:-1, :-1], y[:-1, :-1], z_pd,
         10,							# 设置等高线的条数，和前面保持一致
		colors = 'w',					# 设置等高线的颜色，也可以用cmap设置
		alpha = 1
)
fig.colorbar(cf, ax = ax)
ax.set_title('contourf with levels')
plt.show()

输出图像如下：

八、箱线图和小提琴图

1、箱线图：plt.boxplot()

箱线图绘制的是每个列数据的箱体和异常点。使用plt.boxplot函数，它的详细参数介绍如下：

（1）notch，若为False则绘制一个长方形，若为True则绘制一个槽口，这个刻槽描述了在中位数上下的置信区间。
（2）sym，异常点的表示形式，如果为空字符串或None则不绘制，否则类似于11.2.2节末尾的解读标记点字符串的方式绘制异常值的点。
（3）vert，设置图像是否水平或若为True，则表示为垂直绘图，否则为水平绘图
（4）whis，计IQR为上下四分位数（Q1和Q3）的差，指示低于Q1 - whis * IQR和高于Q3 + whis * IQR的值作为异常值并指示
（5）positions，指示先后绘制的列的下标顺序，默认是range(1, N+1)
（6）widths，绘制箱体的宽度。
（7）showmeans，指示是否显示箱体的平均值。

具体示例如下：

plt.figure()
plt.boxplot(np.array(trees),
            notch = True, 
            sym = 'b+', 			# 异常点绘制蓝色的加号
            vert = True, 
            whis = 1, 
            positions = [3, 2, 1], 
            widths = 0.4, 
            showmeans = True
)
plt.show()

输出图像如下：

2、小提琴图：plt.violinplot()

小提琴图是同时描述数据上下分布和数据密度的图形，使用plt.violinplot函数，提琴的主要参数介绍如下，和箱线图的主要参数很相似：

（1）vert：若为True，则表示为垂直绘图，否则为水平绘图。
（2）widths：绘制小提琴的宽度。
（3）positions：同箱线图，指示先后绘制的列的下标顺序，默认是range(1, N+1)。
（4）showmeans：指示是否显示平均值。
（5）showextrema：指示是否显示异常值。
（6）showmedians：指示是否显示中位数

在此，我们同样用一个例子来综合运用上面各个参数，来展示各参数实际效果：

plt.figure()
plt.violinplot(np.array(trees),
           vert = True, 
           widths= 0.6, 
           positions = [3, 2, 1], 
           showmeans = True,  
           showextrema = True, 
           showmedians = True, 
)
plt.show()

输出图像如下：

以上就是在数据分析中常用到的可视化图形，下节我们将补充对于图形属性设置函数的讲解。

---

对于缺乏Python基础的同仁，可以通过免费专栏《Python学习笔记（基础）》从零开始学习Python

结语

请始终相信“Done is better than perfect” ，不要过分追求完美，即刻行动就是最好的开始， 一个模块一个模块地积累和练习，必将有所收获。
还有其他的问题欢迎在评论区留言！

---

[版权申明] 非商业目的注明出处可自由转载，转载请标明出处！！！
博客：butterfly_701c