关于死锁的原因及解决方案

死锁的几种情况

1. 一个线程一把锁, 可重入锁没事, 不可重入锁可能会死锁.(锁里加锁)

2. 两个线程两把锁, 即使是可重入锁也可能会死锁.

这个情况如下:

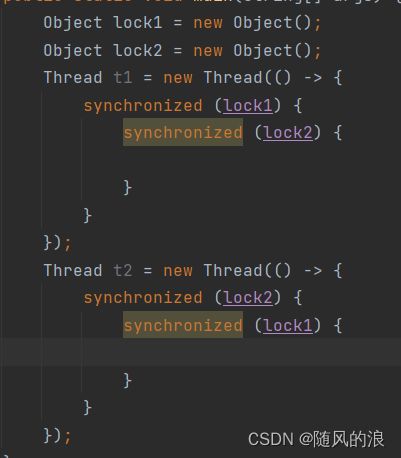
假设线程 t1 和线程 t2 同时都拿到了第一把锁, 然后再获取第二把锁时, 就会产生阻塞等待, 因为另一把锁被另一个线程占用了, 所以两把锁都会一直处以阻塞等待状态, 即产生了死锁.

4. N 个线程 M 把锁, 线程数量更多, 锁数量也更多了, 更容易死锁.

情况就比较复杂了, 我们举一个经典例子 : 哲学家就餐问题

假设有五个哲学家吃饭, 他们面前摆了 5 根筷子, 对 不是无双, 是五根.
具体场景如下:

假设他们拿起筷子和放下筷子是随机的, 如果筷子被别人拿了, 就阻塞等待一会, 等的过程中不会放弃自己手里的筷子.

假设他们同时拿起左手的筷子 或者 同时拿起右手的筷子, 那就产生死锁了.(他们都在等别人放下筷子, 都在相互等待)

这些哲学家就相当于一个个线程, 筷子就是锁.
对于线程来说, 上述情况会更加复杂.

死锁的四个必要条件

总结一下上面几种情况, 我们发现死锁有几个必要条件(缺一不可) :

1. 互斥使用. 一个线程拿到一把锁后, 另一个线程不能使用. (锁的基本特点)
2. 不可抢占. 一个线程拿到锁, 只能自己主动释放, 不能被其他线程强行占有. (锁的基本特点)
3. 请求和保持. 比如锁里加锁, 一个线程拿到了锁, 还没释放锁, 就又想加锁, 这不就是 “吃着碗里的,想着锅里的” 吗. (代码特点)
4. 循环等待. 上面几个死锁例子都是依赖循环等待的. (代码特点)

如何避免解决死锁

既然上述四个情况缺一不可, 那我们想办法破其一, 那就可避免死锁了.

显然1, 2 点都是锁的基本特点, 不能改变. 第 3 点也破坏不了, 除非锁里不加锁, 但这不是我们要的答案.

也就只有第 4 点容易破坏了, 我们可以运用锁排序, 什么意思呢?

假设有 N 个线程尝试获取 M 把锁, 就可以针对 M 把锁进行编号(1, 2, 3…M).N 个线程尝试获取锁的时候, 都按照固定的按编号由小到大顺序来获取锁. 这样就可以避免循环等待

就像这样 :

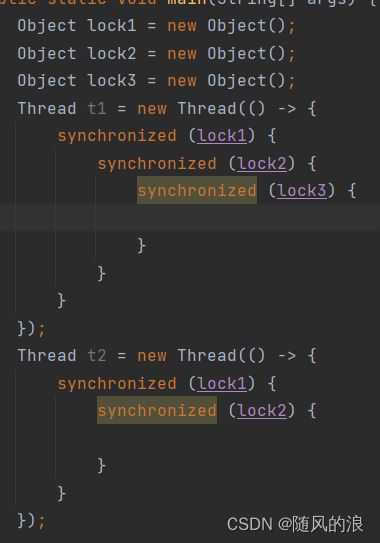
这样当线程 t1 进入锁获取到 lock1 锁对象后, t2 线程就不会进入锁了, 而是阻塞等待, 直到 t1 线程释放了锁对象.

针对哲学家就餐问题, 我们用这个方法来解决下.
我们将 5 根筷子标好序号, 如下 :

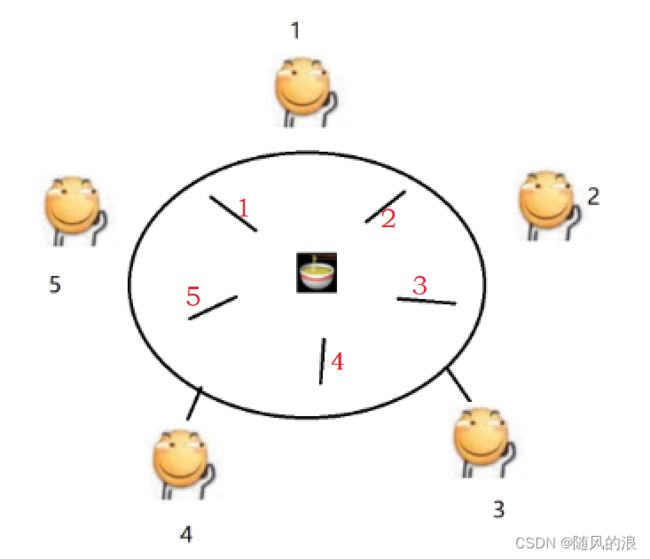
我们规定一号先拿 1 号筷子再拿 2 号筷子, 二号先拿 2 号筷子再拿 3 号筷子,
三号先拿 3 号筷子再拿 4 号筷子, 四号先拿 4 号筷子再拿 5 号筷子, 五号先拿 1 号筷子再拿 5 号筷子.
假设最坏的情况, 也就是一号到四号都拿到了自己编号相同的筷子, 这时轮到五号了, 他一看, 一号被占了, 那他也就不会拿五号筷子了, 这样四号就能拿到 两根筷子了, 他一用完, 三号就能拿到筷子了, 以此类推所有人都能吃上饭了.