算法学习 （门徒计划）4-3 专项面试题解析 学习笔记

前言

（7.29继续学习-第六章第3节： 2021.07.29 专项面试题解析）

4-3 开课吧第十二讲专项面试题解析
以下一共12题(可能也没有)

9.47~11.28; 1.5H
12.30~13.38;1H
14.40~ 17.15;2.5H
20.00~01.00;5H
10.40~11.27;0.5H
总计（10.5H加上课时的4.5H）15H，超过了3倍耗时，需要反思。

LeetCode 1367. 二叉树中的列表

链接：https://leetcode-cn.com/problems/linked-list-in-binary-tree

给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。

如果在二叉树中，存在一条一直向下的路径，且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值，那么请你返回 True ，否则返回 False 。

一直向下的路径的意思是：从树中某个节点开始，一直连续向下的路径。

解题思路

本题显然是跟着二叉树进行向下递归，期望找到从某一个节点后能够有连续的递归内容跟链表相同。

（这题很简单）

示例代码

(1ms、38.6MB)

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSubPath(ListNode head, TreeNode root) {
        if(head==null)return true;
        if(root == null) return false;
        if(head.val == root.val&&isMySubPath(head,root)){
            return true;
        }
        return isSubPath(head,root.left)||isSubPath(head,root.right);
    }

    public boolean isMySubPath(ListNode head, TreeNode root) {
        if(head==null)return true;
        if(root == null) return false;

        if(head.val == root.val){
            return  isMySubPath(head.next,root.left)||isMySubPath(head.next,root.right);
        }
        return false;
    }
}

LeetCode 958. 二叉树的完全性检验

链接：https://leetcode-cn.com/problems/check-completeness-of-a-binary-tree

给定一个二叉树，确定它是否是一个完全二叉树。
百度百科中对完全二叉树的定义如下：

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1~ 2h 个节点。）

解题思路

方案1

准备广搜，每次提取出当前节点后进行判断，如果存在左枝空缺或者右枝空缺则进行标记，当出现左枝空缺但是有右枝时立即返回false，当出现右枝空缺时，如果后续出队列的节点依然有子树则反回false，否则全部出队列后认为true。（入队方式为，出队后，将左右子节点入队）

但是这样性能不好。

（课上的思路如下）
方案二

知道完全二叉树的总节点数后，就可以计算出左子树应该有多少个节点，右子树有多少个节点。

另外完全二叉树的子树也是完全二叉树，因此进行向下递归判断左右子树是否都是完全二叉树。

而完全二叉树从节点数考虑特征，最后一层前（假设当前深度为m）的节点总数为（2m-1个），最后一层中属于左子树的节点不会超过m个。

由此得出左右子树应该持有的节点数为（其中m是最后一层前的深度，l表示是最后一层中左子树持有的节点数，r是最后一层中右子树持有的节点数）：

• 左：m-1+l
• 右：m-1+r
  （这题可以用广搜解，但是本次用课上思路）

示例代码

(0ms，37.2MB)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isCompleteTree(TreeNode root) {
        if(root==null) return true;

        int n = getTreeCnts(root);
        int m=1,cnt = 1;
        while(cnt + 2*m<n){
            m*=2;
            cnt +=m;
        }
        //System.out.println("n:"+n+"m:"+m);
        return judge(root ,n,m);
    }

    private boolean judge(TreeNode root,int n,int m){
        if(root ==null) return n==0;
        if(n==0) return false;
        if(n == 1 ) {
            return root.left ==null &&root.right ==null;
        }
        int k= Math.max(2*m -1,0);
        int l = Math.min(m,n-k),r = n-k-l;
   
        return judge(root.left,(k-1)/2+l,m/2)&&judge(root.right,(k-1)/2+r,m/2);
    }

    private int getTreeCnts(TreeNode root){
        if(root ==null) return 0;
        return 1+getTreeCnts(root.left)+getTreeCnts(root.right);
    }
}

LeetCode 剑指 Offer 36. 二叉搜索树与双向链表

链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

解题思路

本题是一个对于二叉树进行中序遍历，最终将遍历生成序列串联成双向链表，并且收尾相连。
（最终对外的链表头结点为原始二叉树最左侧的节点、也就是中序遍历后的第一个节点）

并且利用原本的二叉树的两个指针域用作双向链表指向前一位和后一位的作用。

由此本题的核心思路就是中序遍历，并且在遍历的过程中将节点串联拼接形成结果

（我的解题思路为）

先设计一套中序遍历的代码，并且准备一个数据结构存储遍历的节点，最终全部中序遍历完成后根据这个数据结构从头遍历一次将每个节点的指针域改为指向前后节点

（课上的思路为）

在中序遍历的过程中就进行拼接

（显然比我的思路性能好）

示例代码

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;
        pre = null;//尾节点
        head = null;//头节点
        in_order(root);
        head.left = pre;
        pre.right = head;
        return head;
    }

    private Node head,pre;
    private void in_order(Node root){
        if(root == null) return ;

        //左遍历
        in_order(root.left);

        //以下当原始准备串联的链表尾部还未确定时，定义链表的头部
        if(pre ==null)
            head = root;
        else
            pre.right = root;

        //接上左侧的遍历结果，接上左枝干的尾部
        root.left = pre;

        //左遍历的结果和根节点合并，尾部指针表示为当前队列末尾
        pre = root;

        //右遍历
        in_order(root.right);
    }
}

LeetCode 464. 我能赢吗

链接：https://leetcode-cn.com/problems/can-i-win

在 “100 game” 这个游戏中，两名玩家轮流选择从 1 到 10 的任意整数，累计整数和，先使得累计整数和达到或超过 100 的玩家，即为胜者。

如果我们将游戏规则改为 “玩家不能重复使用整数” 呢？

例如，两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数（不放回），直到累计整数和 >= 100。

给定一个整数 maxChoosableInteger （整数池中可选择的最大数）和另一个整数 desiredTotal（累计和），判断先出手的玩家是否能稳赢（假设两位玩家游戏时都表现最佳）？

你可以假设 maxChoosableInteger 不会大于 20， desiredTotal 不会大于 300。

示例：

输入：
maxChoosableInteger = 10
desiredTotal = 11

输出：
false

解释：
无论第一个玩家选择哪个整数，他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1，那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10（那么累积和为 11 >= desiredTotal），从而取得胜利.
同样地，第一个玩家选择任意其他整数，第二个玩家都会赢。

解题思路

本题在于如何判断先手的人能否赢，由于假想两位玩家游戏时都表现最佳，因此就是判断对手是否会输。

对于这种取数的解法，如果跟枚举相关，那么就通常要使用问题求解树来进行计算。因此准备深搜的思想并且用记忆化进行历史使用情况的排除。

（另外可以在计算前可以排除一些不可能达到的情况）

本题的核心在于如何进行记忆化进行问题求解树重叠情况的排除，而需要记忆的内容仅为本次使用的数（因为其他值比如剩余值是随着使用的数变化的，而上限值也是固定的）

（代码略）

LeetCode 172. 阶乘后的零

链接：https://leetcode-cn.com/problems/factorial-trailing-zeroes

给定一个整数 n，返回 n! 结果尾数中零的数量。

示例 1:
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。

示例 2:
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.

解题思路

每有一个零就表示在相乘的过程中生成了一个含有零的因数，因此能统计出多少个结果含有0的因数相乘最终结果中就有多少个0

而能生成零的数，基本就是2*5，而通常能找的5因数的情况下至少能找到2个2的因数，因此本题就是找上限到n数中一共能拆解出多少个5作为因数
（获取因数时对于5的阶乘，例如25，一次能拆解出2个因数）

示例代码

class Solution {
    public int trailingZeroes(int n) {
        int cnt =0,m=25;
        cnt += n/5;
        while(m<=n){
            cnt += n/m;
            m*=5;
        } 
        return cnt;
    }
}

LeetCode 384. 打乱数组

链接：https://leetcode-cn.com/problems/shuffle-an-array

给你一个整数数组 nums ，设计算法来打乱一个没有重复元素的数组。

实现 Solution class:

• Solution(int[] nums) 使用整数数组 nums 初始化对象
• int[] reset() 重设数组到它的初始状态并返回
• int[] shuffle() 返回数组随机打乱后的结果

示例：

输入
["Solution", "shuffle", "reset", "shuffle"]
[[[1, 2, 3]], [], [], []]
输出
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]

解释
Solution solution = new Solution([1, 2, 3]);
solution.shuffle();    // 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。例如，返回 [3, 1, 2]
solution.reset();      // 重设数组到它的初始状态 [1, 2, 3] 。返回 [1, 2, 3]
solution.shuffle();    // 随机返回数组 [1, 2, 3] 打乱后的结果。例如，返回 [1, 3, 2]

解题思路

由于期望获得数组的初始状态因此原始数组不可被打乱，或者准备一个空间存着原始数组用于后期取用，那么从这个角度看，能够打乱的就只是原始数组各个元素的下标了

本题主要操作是怎么随机各个元素的下标

java中随机数生成的方式为：

• 通过java.Math包的random方法得到1-10的int随机数
• 公式是:最小值—最大值（整数）的随机数
• 类型:最小值+Math.random()*最大值
• 或者new Random.nextInt(n);生成一个0~n随机整数（不包含n）

（代码略）

LeetCode 437. 路径总和 III

链接：https://leetcode-cn.com/problems/path-sum-iii

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

解题思路

本题显然是求从任意节点开始是否能存着向下连续递归的节点值之和能够等于目标值。这题简单考虑就是一个深度搜索，由于节点值可以为负数，因此每个节点都必须被遍历。
最终期望统计出能有多少条路径。

（这是我的思路有更好的办法吗？）

有，将所有节点的路径从根开始的值所生成的和（前缀和）存入一个哈希表（表的key值为前缀和，value值为该前缀和在当前路线上出现的次数），从而方便获取期望的情况。

（这种解法的优势在于，能够获取当前路径任何一段的值而不需要从某一段的起始重复的进行遍历）

由于在递归过程中，回溯时，会将支路上统计的前缀和清空（清除自身提供的前缀和数计数），由此确保当前存储的都是从根节点到当前所能持有的所有前缀和状态。

示例代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private HashMap<Integer,Integer> h;

    //到当前节点的前缀和计算
    private int count (TreeNode root,int sum,int targetSum){
        if(root == null) return 0;
        sum += root.val;
        if(h.get(sum-targetSum)==null)
            h.put(sum-targetSum,0);
        int ans = h.get(sum-targetSum);
        if(h.get(sum)==null)
            h.put(sum,0);
        //存入自身所在路线能提供的可行性计数，当前路线上成立的sum次数
        h.put(sum,h.get(sum)+1);
        //加上下方枝干的结果
        ans += count(root.left , sum ,targetSum);
        ans += count(root.right, sum ,targetSum);
        //清除自身所在路径能提供的可行性计数
        h.put(sum,h.get(sum)-1);
        return ans;
    }

    public int pathSum(TreeNode root, int targetSum) {
        h= new  HashMap<Integer,Integer>();
        h.put(0,1);
        return count(root, 0, targetSum);
    }
}

LeetCode 395. 至少有 K 个重复字符的最长子串

链接：https://leetcode-cn.com/problems/longest-substring-with-at-least-k-repeating-characters

给你一个字符串 s 和一个整数 k ，请你找出 s 中的最长子串， 要求该子串中的每一字符出现次数都不少于 k 。返回这一子串的长度。

示例 1：

输入：s = “aaabb”, k = 3
输出：3
解释：最长子串为 “aaa” ，其中 ‘a’ 重复了 3 次。

示例 2：

输入：s = “ababbc”, k = 2
输出：5
解释：最长子串为 “ababb” ，其中 ‘a’ 重复了 2 次， ‘b’ 重复了 3 次。

解题思路

本期期望寻找某一处最长子串，在该子串中，每一元素的出现次数都不少于k

简单考虑为枚举所有子串，然后寻找长度最长的。

记录子串中字符出现的方法为哈希表（key为字符，value为出现次数）或者一个长度为26的数组，如果是哈希表，只存储出现次数小于k次的字符。

但是枚举的方案是低性能的，因此换一个获取子串的思路。

（课上获取子串的思路如下）

• 首先统计所有字符的数量，那些本身就总数小于k次的字符哪怕合并整个总字符串都不可能完成条件因此，这些字符将总字符串分割成了若干小段，
• 同理每一段内也可以用这种方式获取分割点，当某一个子串不能再获取新的分割点时，这个子串就是自身范围内的最大子串，
• 统计所有区间的大小，最终得出最大的无需分割区间

（在过程中如果子区间的大小已经小于之前其他地方获取的最大子串，则无需讨论这个区域内的情况）

（为了简易的进行区间划分因此认为字符串末端也是一个分割点）

本题的核心思路在于分制的思想，根据某种条件模板化的进行分割。

示例代码

class Solution {
    private int maxLen=0;
    public int longestSubstring(String s, int k) {
        char [] c = s.toCharArray();
        getLongestSection(c,0,c.length,k);

        return maxLen;
    }

    private void getLongestSection( char [] c,int start,int end ,int k){
        int [] key = new int [26];
        for(int i= start;i<end;i++){
            key[c[i]-'a']++;
        }
        ArrayList <Integer> ends = new ArrayList <Integer>();
        for(int i=start;i<end;i++){
            if(key[c[i]-'a']<k)
                ends.add(i);
        }
        ends.add(end);
        // for(int e:ends){
        //     System.out.println("---end:"+e);
        // }
        if(ends.size()<=1){
            maxLen = maxLen<end-start?end-start:maxLen;
            return ;
        }
        for(int i=0;i<ends.size();){
            if(ends.get(i)-start<=maxLen) {
                start = ends.get(i++)+1;
                continue;
            }
            //System.out.println("s:"+start+"end:"+ends.get(i)+","+i);

            getLongestSection(c,start,ends.get(i),k);
            start = ends.get(i)+1;

        }
    }
}

LeetCode 190. 颠倒二进制位

链接：https://leetcode-cn.com/problems/reverse-bits

颠倒给定的 32 位无符号整数的二进制位。

提示：

• 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
• 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

进阶:
如果多次调用这个函数，你将如何优化你的算法？

示例 1：

输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

解题思路

方案一：遍历
初步考虑先将数转化为二进制数组，进行颠倒，再将二进制数组合成数值

基于这个思路可以稍微优化一下，不转换为2进制，而是直接以2进制的位指针进行偏移，偏移时头和尾进行互换，当头和尾相遇时循环结束

进一步简化就是从低位一步步的放到目标结果的高位。

（但是学习解法的过程中，我发现了另一个极好的解法，源自官方，如下）

方法二：位运算分治
链接：https://leetcode-cn.com/problems/reverse-bits/solution/dian-dao-er-jin-zhi-wei-by-leetcode-solu-yhxz/

思路

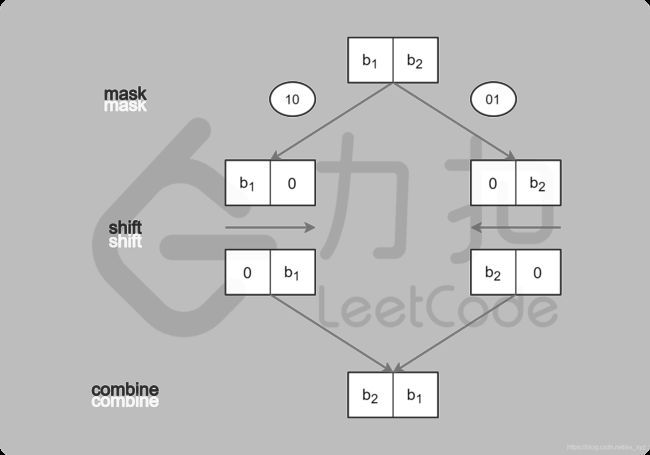
若要翻转一个二进制串，可以将其均分成左右两部分，对每部分递归执行翻转操作，然后将左半部分拼在右半部分的后面，即完成了翻转。

由于左右两部分的计算方式是相似的，利用位掩码和位移运算，我们可以自底向上地完成这一分治流程。

对于递归的最底层，我们需要交换所有奇偶位：

• 取出所有奇数位和偶数位；
• 将奇数位移到偶数位上，偶数位移到奇数位上。
• 类似地，对于倒数第二层，每两位分一组，按组号取出所有奇数组和偶数组，然后将奇数组移到偶数组上，偶数组移到奇数组上。以此类推。

需要注意的是，在某些语言（如 \texttt{Java}Java）中，没有无符号整数类型，因此对 nn 的右移操作应使用逻辑右移。

（对于这个解法我理解一下）

本质上也是位进行交换，但是在交换时，采用分制的想法，第一层最小区间是2，因此所有数字两两互换。第二层则是最小区间为4，第三层是8，第四层是16，通过这种方式实现了依次交换

这种方式之所以能够在此处使用根本原因在于计算机的位运算是单轮次的，而循环则是每一步一个轮次，所以才实现了极高的效率。

（以下的两个代码都是从官方解法而来）
（但是最终判断性能，发现二者性能基本一致）

示例代码

（解法1）

public class Solution {
    public int reverseBits(int n) {
        int rev = 0;
        for (int i = 0; i < 32 && n != 0; ++i) {
            rev |= (n & 1) << (31 - i);
            n >>>= 1;
        }
        return rev;
    }
}

（解法2）

public class Solution {
    private static final int M1 = 0x55555555; // 01010101010101010101010101010101
    private static final int M2 = 0x33333333; // 00110011001100110011001100110011
    private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111
    private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111

    public int reverseBits(int n) {
        n = n >>> 1 & M1 | (n & M1) << 1;
        n = n >>> 2 & M2 | (n & M2) << 2;
        n = n >>> 4 & M4 | (n & M4) << 4;
        n = n >>> 8 & M8 | (n & M8) << 8;
        return n >>> 16 | n << 16;
    }
}

LeetCode 8. 字符串转换整数 (atoi)

链接：https://leetcode-cn.com/problems/string-to-integer-atoi

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

• 读入字符串并丢弃无用的前导空格
• 检查下一个字符（假设还未到字符末尾）为正还是负号，读取该字符（如果有）。 确定最终结果是负数还是正数。 如果两者都不存在，则假定结果为正。
• 读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
• 将前面步骤读入的这些数字转换为整数（即，“123” -> 123， “0032” -> 32）。如果没有读入数字，则整数为 0 。必要时更改符号（从步骤 2 开始）。
• 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被固定为 −231 ，大于 231 − 1 的整数应该被固定为 231 − 1 。
• 返回整数作为最终结果。

注意：

• 本题中的空白字符只包括空格字符 ’ ’ 。
• 除前导空格或数字后的其余字符串外，请勿忽略 任何其他字符。

示例 1：

输入：s = "42"
输出：42
解释：加粗的字符串为已经读入的字符，插入符号是当前读取的字符。
第 1 步："42"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："42"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："42"（读入 "42"）
           ^
解析得到整数 42 。
由于 "42" 在范围 [-231, 231 - 1] 内，最终结果为 42 。

解题思路

首先本题可以准备一个最大和最小数字的模板，如果发现会超上限就直接返回上限。

然后本题就只需要逐个字符进行数值的拼接即可

简单考虑甚至可以用库函数直接进行转换，最多是转换前删除多余的空格和0和符号。

（以上是我的思路，课上的解法如下）

按位进行数字组合，其中关键操作里有个上限判断，当临界正数上限时，如果超过了这个上限那么就根据正负的标志生成正数上限或者负数上限

（核心操作是一样的，区别在于一个极限考虑，我的方案优势在于我可以在计算前就得知几种会超上限的情况）

（示例代码略）

LeetCode 380. O(1) 时间插入、删除和获取随机元素

链接：https://leetcode-cn.com/problems/insert-delete-getrandom-o1

设计一个支持在平均 时间复杂度 O(1) 下，执行以下操作的数据结构。

1. insert(val)：当元素 val 不存在时，向集合中插入该项。
2. remove(val)：元素 val 存在时，从集合中移除该项。
3. getRandom：随机返回现有集合中的一项。每个元素应该有相同的概率被返回。

示例 :

// 初始化一个空的集合。
RandomizedSet randomSet = new RandomizedSet();

// 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomSet.insert(1);

// 返回 false ，表示集合中不存在 2 。
randomSet.remove(2);

// 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomSet.insert(2);

// getRandom 应随机返回 1 或 2 。
randomSet.getRandom();

// 从集合中移除 1 ，返回 true 。集合现在包含 [2] 。
randomSet.remove(1);

// 2 已在集合中，所以返回 false 。
randomSet.insert(2);

// 由于 2 是集合中唯一的数字，getRandom 总是返回 2 。
randomSet.getRandom();

解题思路

本题有一个平均时间复杂度的要求，因此显然想到哈希相关的知识。

首先有一种极为简化的思想就是常数空间法，划分超大的空间可以囊括所有的情况，使得哈希操作不会出现冲突

或者准备一个哈希表。

但是有一个问题，如何能够随机的获取元素呢？

有一个办法为准备一个可变数组，当删除元素时将动态数组末尾的值和待删除的值进行互换，同时哈希表中被影响的值也对应的改变。
而哈希表中（key值为值，value为该值所在动态数组中的坐标）

由此可以用这个动态数组来实现随机获取下标来做到随机获取一个值

示例代码

class RandomizedSet {

    private HashMap<Integer,Integer> h;
    private ArrayList<Integer> arr; 

    /** Initialize your data structure here. */
    public RandomizedSet() {
        h = new HashMap<>();
        arr = new ArrayList<Integer>();
    }
    
    /** Inserts a value to the set. Returns true if the set did not already contain the specified element. */
    public boolean insert(int val) {
        if(h.get(val)==null){
            arr.add(val);
            h.put(val,arr.size()-1);
            return true;
        }
        return false;
    }
    
    /** Removes a value from the set. Returns true if the set contained the specified element. */
    public boolean remove(int val) {
        if(h.get(val)!=null){
            int temp = arr.get(arr.size()-1);
            int i = h.get(val);
            arr.set(i,temp);

            h.put(temp,i);
            //System.out.println(arr.size()+"..");
            arr.remove (arr.size()-1);

            h.remove(val);
            return true;
        }
        return false;
    }
    
    /** Get a random element from the set. */
    public int getRandom() {
        int index = new Random().nextInt(arr.size());
        return arr.get(index);
        
    }
}

/**
 * Your RandomizedSet object will be instantiated and called as such:
 * RandomizedSet obj = new RandomizedSet();
 * boolean param_1 = obj.insert(val);
 * boolean param_2 = obj.remove(val);
 * int param_3 = obj.getRandom();
 */

LeetCode 402. 移掉 K 位数字

链接：https://leetcode-cn.com/problems/remove-k-digits

给你一个以字符串表示的非负整数 num 和一个整数 k ，移除这个数中的 k 位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

示例 1 ：

输入：num = “1432219”, k = 3
输出：“1219”
解释：移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。

解题思路

本题有2个切入点(实际上是同一个)，一个是尽可能的让高位的数更小，另一个是如果有零在其中，那么如果有可能删除全部零前面的数就尽量删除，因为这样的数字等效于该数和后面跟随的零。
由此准备一个数组，将原始数字切换为原始数和自身后面跟随的零所串联的数，例如：10234007转为{10，2，3，400，7}。

然后根据删除数的规则进行删除。

删除的规则为：

• 从头向后找k位，如果出现大于10的数字，则删除这个数字前面的所有数字n为，并继续向后找k-n位直到没有出现大于10的数字为止。

• 当没有出现大于10的数字时，如果一个数字后方存在比其后相邻的数小就将其删除，持续进行直到删除的数总数达到k位。

这个诉求符合单调栈元素添加的特征，因为单调栈中小的数字就尽可能的在前面，由此原始字符串每个元素入栈时，都以符合单调性的特征进行管理，此时每出栈一个元素k-1，当栈为空时，此时期望入栈的元素为零时，跳过此次入栈。

(下方我用数组代替了栈，用指针表示栈顶)

示例代码

class Solution {
    public String removeKdigits(String num, int k) {
        char [] c  = num.toCharArray();

        char [] cs = new char [c.length]; 
        int csIndex =-1;

        for(int i = 0;i<c.length;i++){
            while( csIndex >=0&&cs[csIndex]>c [i]&& k>0) {
                csIndex --; k--;
            }
            if(c[i]=='0'){
                if(csIndex>=0)
                    cs[++csIndex] = c[i];
            }else
                cs[++csIndex] = c[i];
        }
        csIndex -= k;
        if(csIndex<0)
            return "0";

        StringBuilder sb = new StringBuilder ();
        for(int i=0;i<=csIndex;i++)
            sb.append( cs[i] );
        return sb.toString();
    }
}

LeetCode 316. 去除重复字母

链接：https://leetcode-cn.com/problems/remove-duplicate-letters

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

注意：该题与 1081 https://leetcode-cn.com/problems/smallest-subsequence-of-distinct-characters 相同

示例 1：

输入：s = “bcabc”
输出：“abc”

示例 2：

输入：s = “cbacdcbc”
输出：“acdb”

解题思路

（这题曾经在华为面试时做过，印象很深因为当初我没做出来）

这题和上一题很像，因此一部分代码可以抄过来

首先本题看什么样的字符被剔除后可以使得字典序变小，那就是这个字符在可被剔除（有剩余的重复字符）的情况下，右侧有比其小的字符。

那么这种观察右侧有比其小这样的需求，就是单调栈的特征，因此用单调栈来维护这种特征。

那么操作上，首先获取所有元素的出现次数，只有次数1次以上的才可能入栈（入栈时该元素的出现次数需要减1，这个记录所有元素出现次数的存储内容为栈外元素）。但是所有元素都应该顺次和栈顶元素进行比较，当这个元素比栈顶元素小或者等于时，就另栈顶元素出栈，并且将这个出栈的元素从原始数列中清除。

那么那些没有入栈的元素，就依旧在原始数列中保持位置，最终遍历原始数组中剩余的元素进行拼接生成结果

（进一步思考出现此处1次的元素也可以入栈，但是需要改为不可出栈）
（规则改为）

• 元素入栈的条件为，当前栈内没有该元素,
• 随后在符合出栈规则的情况下进行单调性维护
• 元素出栈的条件为，当前栈外还有元素

示例代码

class Solution {
    public String removeDuplicateLetters(String s) {
        char [] c  = s.toCharArray();
        char [] cs = new char [c.length]; 
        int csIndex =-1;

        int key[] = new int [26];
        boolean [] inStack = new boolean[26];


        for(int i=0;i<c.length;i++)
            key[c[i]-'a']++;
        
        for(int i = 0;i<c.length;i++){
            if(!inStack [c[i]-'a'] ){
                while( csIndex >=0&&cs[csIndex]>=c [i]&& key[cs[csIndex]-'a']>0) {

                    //key[cs[csIndex]-'a']--;
                    inStack [cs[csIndex]-'a'] = false;
                    csIndex --;
                }
                cs[++csIndex] = c[i];
                inStack [c[i]-'a'] = true;
            }
            key[c[i]-'a']--;
        }

        StringBuilder sb = new StringBuilder ();
        for(int i=0;i<=csIndex;i++)
            sb.append( cs[i] );
        return sb.toString();

    }
}

LeetCode 1499. 满足不等式的最大值

链接：https://leetcode-cn.com/problems/max-value-of-equation

给你一个数组 points 和一个整数 k 。数组中每个元素都表示二维平面上的点的坐标，并按照横坐标 x 的值从小到大排序。也就是说 points[i] = [xi, yi] ，并且在 1 <= i < j <= points.length 的前提下， xi < xj 总成立。

请你找出 yi + yj + |xi - xj| 的 最大值，其中 |xi - xj| <= k 且 1 <= i < j <= points.length。

题目测试数据保证至少存在一对能够满足 |xi - xj| <= k 的点。

示例 1：

输入：points = [[1,3],[2,0],[5,10],[6,-10]], k = 1
输出：4
解释：前两个点满足 |xi - xj| <= 1 ，代入方程计算，则得到值 3 + 0 + |1 - 2| = 4 。第三个和第四个点也满足条件，得到值 10 + -10 + |5 - 6| = 1 。
没有其他满足条件的点，所以返回 4 和 1 中最大的那个。

解题思路

前两个点的限制就是当一个点定下后划分的一个选取范围，而这个计算的内容可以视为固定一个点后比如右侧点，进行区间内最值的计算。

那么本题就是一个滑动区间的最值计算方式，因此需要使用单调队列来进行计算。
（以下是我错误的思路）
但是由于每个点都是当前点和区间末尾点计算而来，因此每移动一下区间末尾，都需要重新进行一次单调队列的入队操作。

也就是每一个区间末尾都会独立生成一个最值，最终从这些最值中选出新的最值作为返回值。

因此本题可以理解为二维的单调递减队列。
（但是解题时候遇到了问题，随着右边界进行移动，原本的任何一个点相互计算的结果值也会随之发生改变）
（我的确是在滑动窗口，但是在窗口向右滑动的过程中，如何去时刻的计算窗口内各元素相互组合形成的数值呢，目前是让窗口内所有元素和窗口右端元素进行组合，这个组合的结果可以视为窗口的最值）
（但是超时了也没能使用单调队列的操作）
（显然这种解法是错误的，重新回到窗口上进行考虑，依旧想象为单调队列）

假设区间右侧已经固定那么此时移动左侧，在什么时候会使得区间最值变小呢，必然是左侧点为计算val值贡献度最大的点移出的时候（因为右侧已经固定，因此影响val的只有左侧的点），由于x的单调性已知，因此左侧点对于val的贡献为（yleft-xleft）；

由此只需要把握所有点作为左边界时的贡献度的单调性，再同时进行右边界的平移，就可以时刻把握区间的最值。

（这才是正统的单调队列的应用方式，这题想歪了暴露了我单调队列不熟练的事实，需要加强学习）

因此设计为，向右平移右边界的时候，也作为判断点作为左边界的贡献度（yleft-xleft）的单调性，以此生成一个单调递减队列，这个队列从队首出元素的条件为（xright-xleft>k）,而每一个轮次的区间最值就是队首元素和区间右边界合成的值（yleft-xleft+yright+xright）。

示例代码

class Solution {
    public int findMaxValueOfEquation(int[][] points, int k) {
        LinkedList<Integer> q = new LinkedList<Integer>();
        Integer res =null;
        for(int i=1;i<points.length;i++){
            while(q.size()>0&&getLeftVal(points,q.peekLast())<=getLeftVal(points,i-1))
                q.pollLast();
            q.offer(i-1);

            while(q.size()>0&&points[i][0]-points[q.peek()][0]>k) q.poll();

            if(q.size()==0) continue;

            if(res == null ) 
                res = getVal(points,q.peek(),i);
            else
                res = Math.max(res , getVal(points,q.peek(),i));
        
            
        }
        return res;
    }

    private int getLeftVal(int[][] points,int index){
        return points[index][1]-points[index][0];
    }

    private int getVal(int[][] points,int l,int r){
        //System.out.println (l+"---"+r);
        return points[l][1]+points[r][1]+points[r][0]-points[l][0];
    }
}

LeetCode 321. 拼接最大数

链接：https://leetcode-cn.com/problems/create-maximum-number

给定长度分别为 m 和 n 的两个数组，其元素由 0-9 构成，表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。

说明: 请尽可能地优化你算法的时间和空间复杂度。

示例 1:

输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]

解题思路

（来PK一下耗时22.18~01.00+0.5H，总共3.5H）

本题显而易见就是在获取数有限的情况下，拼一个尽可能大的数字，那么就相当于期望高位尽可能的大，对于这么一个期望值尽可能的大的需求则通常是用单调栈或者单调队列来做的，由于不存在滑动窗口，那么就用单调栈来做。

另外根据期望找到最大值这个需求，那么就要用单调递减栈。

（以下是我的思考路线）
失败的解法一
相比起普通的单调递减栈，这次的入栈选择就变得不一样了，要求尽可能的从两个数列中进行依次取大的数字，但是当剩余的数字和栈内数字数量总和为k时，入栈操作应该取消旧数据出栈需求，最终将这个结果返回。

此外，由于返回的结果是一个固定长度的数组，那么就可以根据这个需求，用这个数组作为栈，栈顶用数组末尾指针表示

（但是这个解法有问题，当依次进行查询时，存在一种可能，某一个很大的数字在其中一个数列的后方，但是等能轮到查看这个数字时栈的长度和剩余数字已经不够了）

失败的解法二
基于这个现象，我提出一个补救的方案，当一个元素被赶出栈时，如果是被另一个数列的元素赶出来的，那么就先存入一个备用栈，当剩余元素不够时，从备用栈中取元素补充进来。

（这个补救方案，我觉得可行，但是需要进一步设计方案）

• 先将两个数列变为单调队列，如果此时这两个单调队列的总长大于等于k，则可以直接用这两个队列拼接选举数字组成答案
• 但是如果两个队列的总长小于k，那么就需要从剩下的内容中进行找补，换句话说从两个队列的末尾分别复原之前被出栈的元素。

由此准备再准备两个备用栈用于存储出栈元素，这两个备用栈的特征是，依次从栈中取的元素，在每一个区间内都是符合单调性的。当外部栈为单调递减栈时，备用栈内元素时一个单调递增栈，栈顶是最大值。

为了能用最少的空间表达最多的数字，改为结果集栈内存数字来源的下标，正数表示来自num1，负数来自num2.

由此首先设计代码完成对原始数组的单调队列获取

（失败了。这个解法没办法处理尾部相同的情况，除此之外都可以求解）
（至此已经尝试了2h，超出面试解题时间范围，我放弃）
（但是我的思路还是可能有借鉴意义的，因此我不想放弃）
（我学习了一下官方的解法，对于我这边采用逻辑的方式进行选择的情况，官方的方案为枚举区间找补情况）
（我不甘心，明天早上再钻研一下）
（我失眠了，最后我意识到我这个解法的后续发展，并且意识到了根本性的矛盾点，这个我会另外写一篇博客来描述：LeetCode 321. 拼接最大数 （错误的解法的进一步思考））

正确解法
（以下是正确的解法）
总体分为3步：

• 首先用单调栈进行对两个序列的单调化从而获得尽可能符合单调性的子序列。
• 随后如果子序列长度和小于k，那么就需要进行补充这个需要补充的长度需要分配给子序列，换句话子序列所在的单调栈在维护单调性的同时还需要关注栈的深度（因此本题是一个单调栈的变种题）
• 最后枚举所有可能的子序列长度补充情况，再在这些长度补充中选择能使得结果最大的情况。（相比起我之前的解法，我是期望用逻辑去选择出最优解，而这个方案是强行解答）

示例代码

（枚举求解,在官方解法上我做了一重优化，近似优化了5%的耗时）

class Solution {

    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int m = nums1.length, n = nums2.length;
        int[] maxSubsequence = new int[k];

        //我插入的优化，先计算出两个序列的单调栈长度，如果长度不满足则进行枚举找补
        int [] q1 = new int [nums1.length];
        int [] q2 = new int [nums2.length];   
        int q1top = -1;
        int q2top = -1;
        for(int i=0;i<nums1.length;i++){
            while(q1top>=0&&nums1[q1[q1top]]<nums1[i])q1top--;
            q1[++q1top] = i;
        }
        for(int i=0;i<nums2.length;i++){
            while(q2top>=0&&nums2[q2[q2top]]<nums2[i])q2top--;
            q2[++q2top] = i;
        }
        //长度已经满足
        if(q2top+q1top+2>=k){
            int i = 0,j=0,index=0;
            while(index<k){
                if(j>q2top||(i<=q1top&&nums2[q2[j]]<nums1[q1[i]])){
                    maxSubsequence[index++] = nums1[q1[i++]]; 
                }else
                    maxSubsequence[index++] = nums2[q2[j++]];
            }
            return maxSubsequence;
        }
        //System.out.println(q1top+"--"+q2top);
        int start = Math.max(q1top,k - n), end = Math.min(k-q2top, m);
        //int start = Math.max(0, k - n), end = Math.min(k, m);

        for (int i = start; i <= end; i++) {
            //System.out.println(i);
            int[] subsequence1 = maxSubsequence(nums1, i);
            int[] subsequence2 = maxSubsequence(nums2, k - i);

            int[] curMaxSubsequence = merge(subsequence1, subsequence2);
            if (compare(curMaxSubsequence, 0, maxSubsequence, 0) > 0) {
                System.arraycopy(curMaxSubsequence, 0, maxSubsequence, 0, k);
            }
        }
        return maxSubsequence;
    }

    public int[] maxSubsequence(int[] nums, int k) {
        int length = nums.length;
        int[] stack = new int[k];
        int top = -1;
        int remain = length - k;
        for (int i = 0; i < length; i++) {
            int num = nums[i];
            while (top >= 0 && stack[top] < num && remain > 0) {
                top--;
                remain--;
            }
            if (top < k - 1) {
                stack[++top] = num;
            } else {
                remain--;
            }
        }
        return stack;
    }

    public int[] merge(int[] subsequence1, int[] subsequence2) {
        int x = subsequence1.length, y = subsequence2.length;
        if (x == 0) {
            return subsequence2;
        }
        if (y == 0) {
            return subsequence1;
        }
        int mergeLength = x + y;
        int[] merged = new int[mergeLength];
        int index1 = 0, index2 = 0;
        for (int i = 0; i < mergeLength; i++) {
            if (compare(subsequence1, index1, subsequence2, index2) > 0) {
                merged[i] = subsequence1[index1++];
            } else {
                merged[i] = subsequence2[index2++];
            }
        }
        return merged;
    }

    public int compare(int[] subsequence1, int index1, int[] subsequence2, int index2) {
        int x = subsequence1.length, y = subsequence2.length;
        while (index1 < x && index2 < y) {
            int difference = subsequence1[index1] - subsequence2[index2];
            if (difference != 0) {
                return difference;
            }
            index1++;
            index2++;
        }
        return (x - index1) - (y - index2);
    }
}

结语

本课为刷题课，也是我首次完整的跟着直播课程学完的课，我在学习过程中最为直观的感觉就是，没有任何一题我能更快更好的提出比课上更好的方法，大部分时候我都跟不上课上的节奏，每一次慢一点点，导致我做不到每一题都跟着写完代码，但是

每一题我都能够在课上理解完毕并写下解题思路，并有空记录一些自身的解题思路。

我相信，通过长期的练习，也许未来我能够在课上较短的时间里，完成代码的编写，和更优方案的思考。

另外本次学习在代码编上还是有很大的不足，部分难题耗时过久，这是自身思维局限性导致的，以后要多加练习。