软件设计师(王勇老师课程)笔记
系列文章目录
这里写目录标题
- 系列文章目录
- 前言
- 一、计算机组成与体系结构
-
- 1.数据表示
- 2.体系结构
- 3.层次化存储
- 4.Cache
- 5.校验码
-
- 1.循环校验码(CRC)
- 2.海明校验码(重点)
- 二、操作系统原理
-
- 1.进程的状态
- 2.前趋图
- 3.进程同步与互斥
- 4.PV操作
- 5.死锁问题
- 6.解决死锁-银行家算法
- 7.分区存储组织
- 8.页面置换算法
- 9.位示图
- 10.微内核操作系统
- 三、数据库系统
-
- 1.关系代数
- 2.范式
- 3.并发控制
- 4.数据备份
- 5.数据仓库和数据挖掘
- 四、计算机网络
-
- 1.DNS协议
- 2.计算机网络的分类-拓扑结构
- 3.网络规划与设计
- 4.子网划分
- 5.特殊含义的IP地址(选择题)
- 6.HTML(出现在选择题)
- 7.IPv6
- 8.信息系统安全属性
- 9.网络安全-各个网络层次的安全保障
- 五、数据结构与算法基础
-
- 1.数组存储地址计算
- 2.稀疏矩阵
- 3.线性表
- 4.数与二叉树
-
- 1.二叉树的各种性质
- 2.二叉树遍历
- 3.树转二叉树
- 3.查找(排序)二叉树
- 4.最优二叉树(哈夫曼树)
- 5.构造哈夫曼树
- 6.线索二叉树
- 7.平衡二叉树
- 8.图
-
- 1.图的存储-邻接矩阵
- 2.图的存储-邻接表
- 3.图-图的遍历
- 4.图-拓扑排序
- 5.图的最小生成树-普利姆算法
- 5.图的最小生成树-克鲁斯卡尔算法
- 9.算法的特性
- 10.算法的复杂度
- 11.查找-顺序查找
- 12.查找-二分查找
- 13.排序
-
- 1.直接插入排序
- 2.希尔排序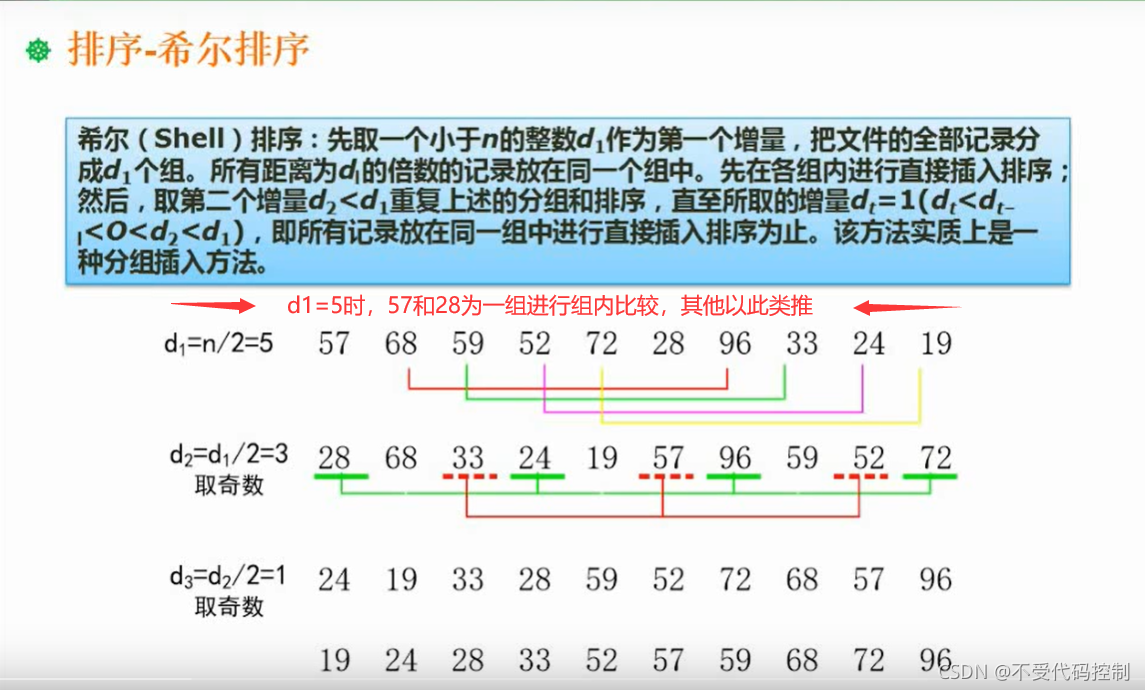
- 3.直接选择排序
- 4.堆排序
- 5.冒泡排序
- 6.归并排序
- 7.快速排序
- 8.基数排序
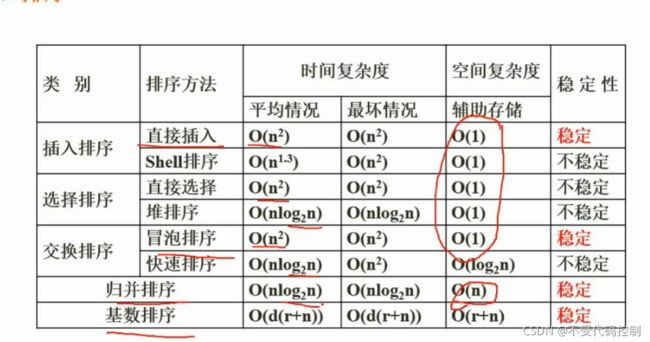
- 14.时间复杂度和空间复杂度
- 8.程序设计与语言处理程序
-
-
- 1.文法
- **2.有限自动机与正规式
-
- 1.有限自动机
- 2.正规式
- 3.例题
- 3.表达式
- 4.传值传址
- 9.法律法规(3分左右)
-
- 1.保护权限
- 2.知识产权人确定
- 3.侵权判定(重点)
- 4.标准化基础知识-标准的编号
- 10.多媒体基础(1-3分)
-
- 1.音频相关概念
- 2.图像相关概念
- 3.媒体的种类
- 4.多媒体的相关计算
-
- 1.例题
- 5.数据压缩
- 10.软件开发模型
-
- 1.瀑布模型
- 2.螺旋模型
- 3.V型
- 4.喷泉模型和RAD
- 5.构建组装模型CBSD
- 6.敏捷开发模型
- 7.结构化设计
- 8.软件测试
- 9.Macabe复杂度(必考)
- 9.CMMI
- 10.项目管理
- 12.面向对象设计
-
- 1.设计原则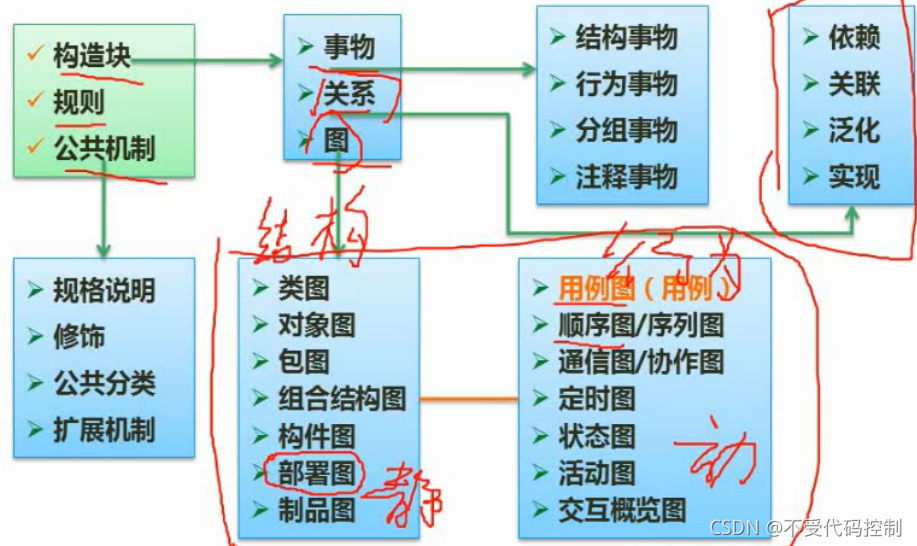
- 2.UML
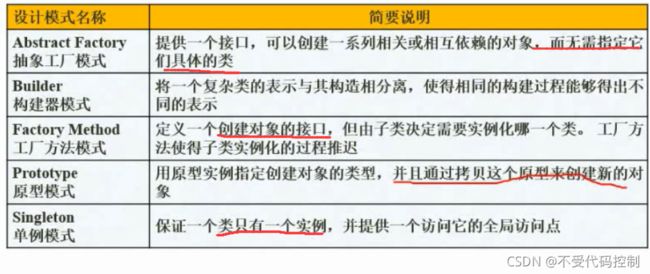
- 3.设计模式的分类
-
- 1.创建型模式
- 2.结构型模式
- 2.行为型模式
- 13.数据流图(重点,分值15分)
-
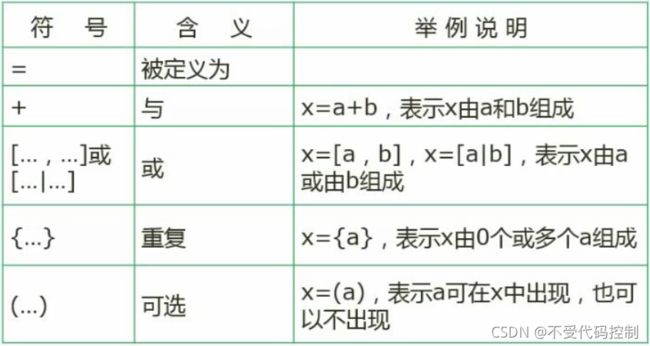
- 1.数字字典
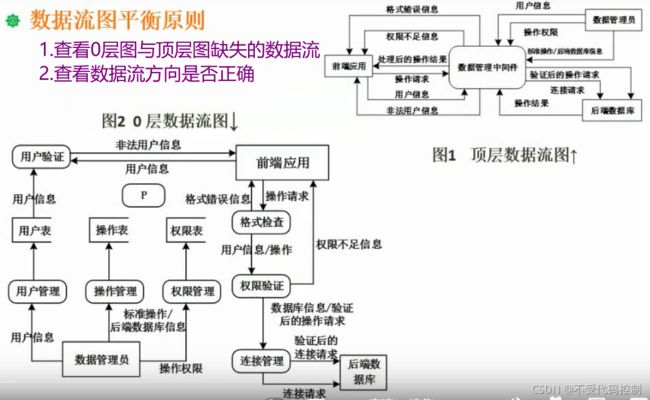
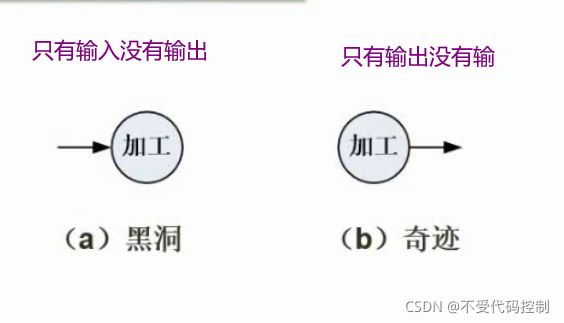
- 2.数据流图平衡原则
- 14.数据库设计(15分)
- 15.UML
-
- 1.用例图
- 2.类图
- 3.顺序图
- 4.活动图
- 16.数据结构与算法应用(下午题,较难)
-
- 1.分治法
- 2.回溯法
- 3.贪心法
- 4.动态规划法
- 1.文法
- 7.归并排序
- 7.归并排序
- 13.排序
- 9.位示图
- 9.位示图
- 9.位示图
- 9.位示图
-
前言
一、计算机组成与体系结构
1.数据表示
R进制转化成十进制:例二进制10100.01=1x24+1x22+1x2^-2
十进制转化R进制:短除法求余,除数为R
二进制转八进制与十六进制:每三个二进制为一组计算八进制,每四个二进制为一组计算十进制
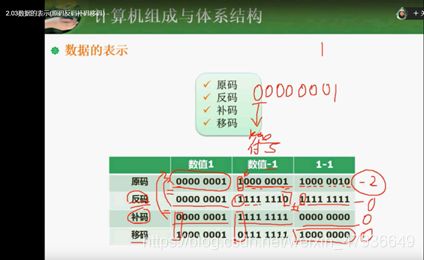
原码:-(2(n-1)-1)~2(n-1)-1
反码:-(2(n-1)-1)~2(n-1)-1
补码:-(2(n-1))~2(n-1)-1
正数:符号位为0;负数:符号位为1;
转换方法:原码->反码:符号位不变,其他为取反;
反码->补码:在反码基础上加1;
补码->移码:正负数都在移码符号位取反;
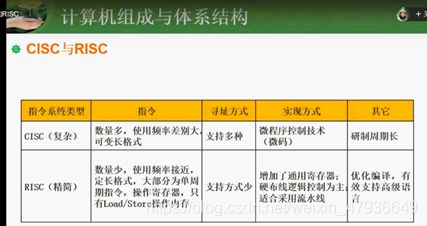
2.体系结构
(2)流水线
流水线计算公式:1条指令执行时间+(指令条数-1)*流水线周期)
实践公式:(k+n-1)*△t k:指令分为几个部分(阶段) △t=流水线周期
图例:(3+100-1)*2=204
流水线吞吐率TP=指令条数/执行时间
流水线最大吞吐量TP(max)=1/△t
加速比=不使用流水线时间/使用流水线时间=500/203
效率E=n个任务占用的时空区/K个流水段总时空区=t/KT

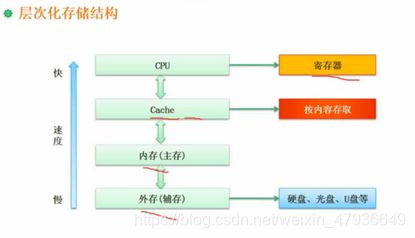
3.层次化存储
4.Cache
Cache+主存储器平均周期=hxt1+(1-h)xt2(h:cache访问命中率,t1:cache周期时间,t2:主存器周期时间,1-h:未命中率)

5.校验码
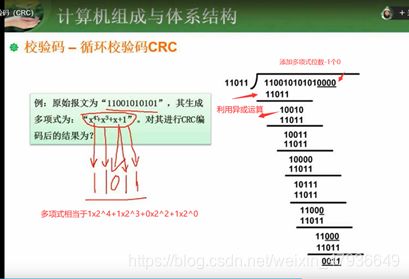
1.循环校验码(CRC)
2.海明校验码(重点)
**利用多组数位的奇偶性来检错和纠错
- List item
**
(1)确认校验码位数:2^r>=k+r+1(k:信息数位数,r:校验码位数)
(2)确认校验码位置:2^n
(3)求出校验码:下面例图
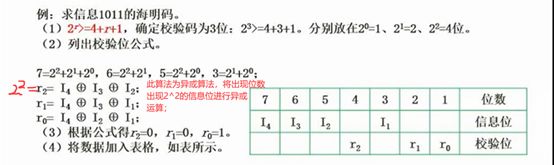
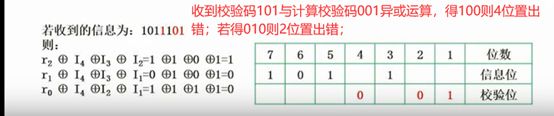
(4)校验码纠正:按上面步骤重新计算校验码并与收到的校验码进行异或运算;
出现1的位置为校验码错误位;
二、操作系统原理
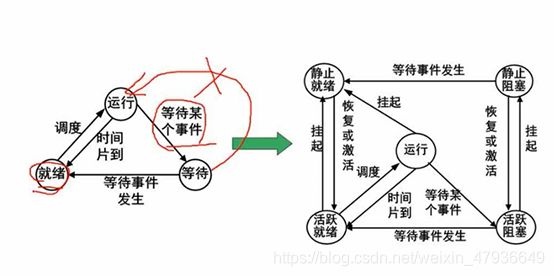
1.进程的状态
2.前趋图
3.进程同步与互斥
4.PV操作
(1)临界资源:诸进程间需要互斥方式对其进行共享资源,如打印机,磁带机
(2)临界区:每个进程中访问临界资源的那段代码
(3)信号量:是一种特殊的变量
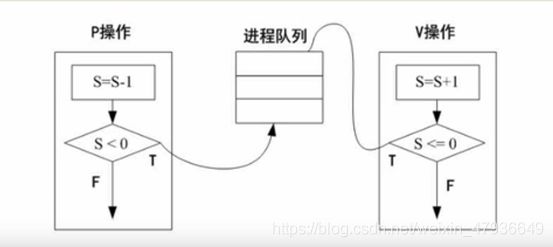
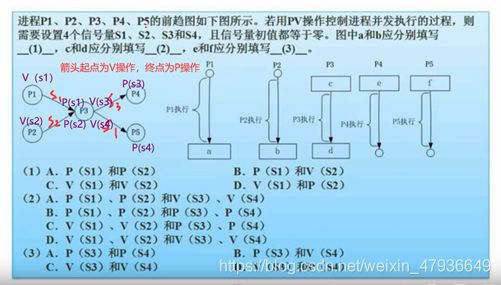
练习:
答案:C,A,A
5.死锁问题
一个进程在等待一件不可能发生的事,则进程就死锁了;一个或多个进程产生死锁,就会造成系统死锁;
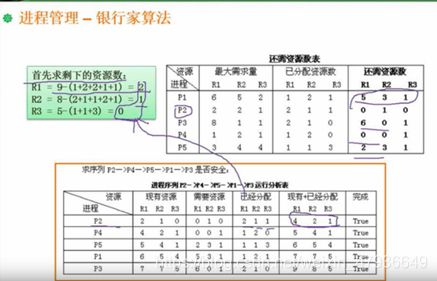
6.解决死锁-银行家算法
7.分区存储组织
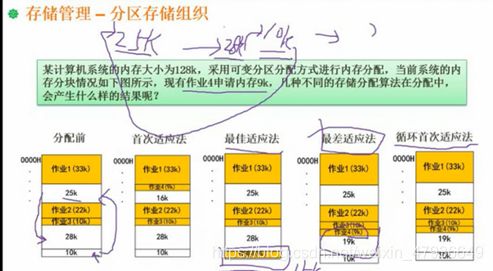
(1)首次适应算法。对可变分区方式可采用首次适应算法,每次分配时,总是顺序查找未分配表,找到第一个能满足长度要求的空闲区为止。
(2)最佳适应算法。可变分区方式的另一种分配算法是最佳适应算法,它是从空闲区中挑选一个能满足作业要求的最小分区,这样可保证不去分割一个更大的区域,使装入大作业时比较容易得到满足。
( 3)最坏适应算法。最坏适应算法 是挑选一个最大的空闲区分割给作业使用,这样可使剩下的空闲区不至于太小,这种算法对中、小作业是有利的。
(4)循环首次适应算法:每次为进程分配空间的时候,从上一次刚分配过的空闲区的下一块开始寻找
8.页面置换算法
1.最佳置换算法(OPT)(理想置换算法):从主存中移出永远不再需要的页面;如无这样的页面存在,则选择最长时间不需要访问的页面。于所选择的被淘汰页面将是以后永不使用的,或者是在最长时间内不再被访问的页面,这样可以保证获得最低的缺页率。
2.先进先出置换算法(FIFO):是最简单的页面置换算法。这种算法的基本思想是:当需要淘汰一个页面时,总是选择驻留主存时间最长的页面进行淘汰,即先进入主存的页面先淘汰。其理由是:最早调入主存的页面不再被使用的可能性最大。 会出现抖动
3.最近最久未使用(LRU)算法:这种算法的基本思想是:利用局部性原理,根据一个作业在执行过程中过去的页面访问历史来推测未来的行为。它认为过去一段时间里不曾被访问过的页面,在最近的将来可能也不会再被访问。所以,这种算法的实质是:当需要淘汰一个页面时,总是选择在最近一段时间内最久不用的页面予以淘汰。不 会出现抖动
4. 时钟(CLOCK)置换算法
算法执行如下操作步骤:
1从指针的当前位置开始,扫描帧缓冲区。在这次扫描过程中,对使用位不做任何修改。选择遇到的第一个帧(u=0, m=0)用于替换。
2如果第1)步失败,则重新扫描,查找(u=0, m=1)的帧。选择遇到的第一个这样的帧用于替换。在这个扫描过程中,对每个跳过的帧,把它的使用位设置成0。
3如果第2)步失败,指针将回到它的最初位置,并且集合中所有帧的使用位均为0。重复第1步,并且如果有必要,重复第2步。这样将可以找到供替换的帧。
参考链接
9.位示图
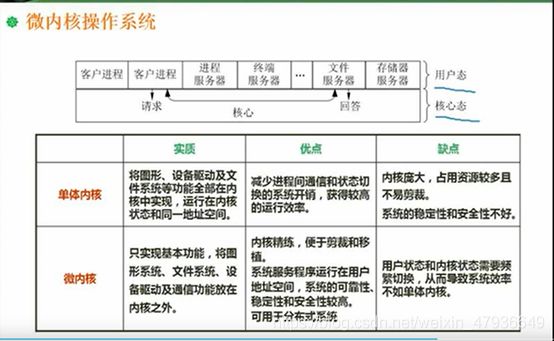
10.微内核操作系统
三、数据库系统
1.关系代数
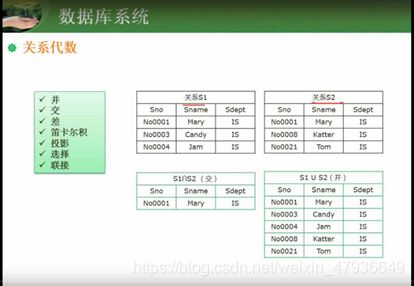
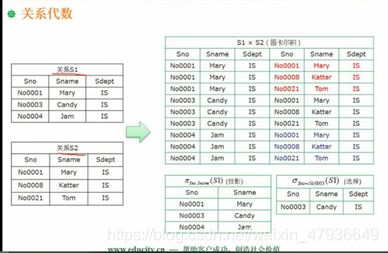
(1)笛卡尔积:前面是S1,后面S2.S1映射S2。不会把相同的列去掉;S2放在S1后面
(2)投影:选出投影的列
(3)选择:选出行
(4)连接:默认选出相同的字段作等值,会把相同的列去掉一个;
(5)
2.范式
候选键:
1.将关系模式的函数依赖关系用“有向图”的方式表示
2.找入度为0的属性,并以该属性集合为起点,尝试遍历有向图,若能正常遍
历图中所有结点,则该属性集即为关系模式的候选键
3.若入度为0的属性集不能遍历图中所有结点,则需要尝试性的将一些中间结点(既有入度,也有出度的结点)并入入度为0的属性集中,直至该集合能遍历所有结点,集合为候选键
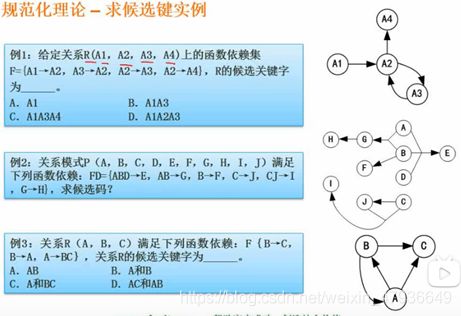
函数依赖
(1)部分函数依赖:(A,B)->C
(2)传递函数依赖:A->C,B->C且B不能确定A
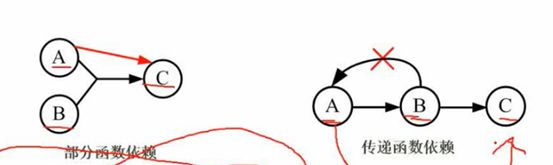
范式
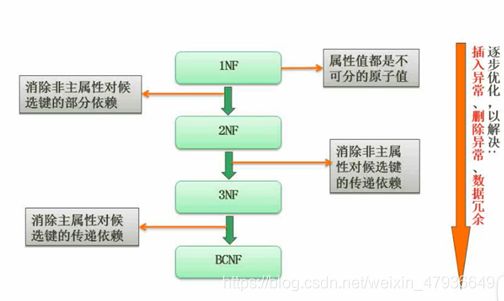
3.并发控制
事务:原子性,一致性,隔离性,持续性
4.数据备份
(1)完全备份:备份所有数据
(2)差量备份:仅备份上一次完全备份之后变化的数据
(3)增量备份:备份上一次备份之后的数据
5.数据仓库和数据挖掘
(1)数据仓库和数据挖掘:面向主题,集成的,相对稳定的(非易失的),反映历史的
(2)数据挖掘方法:决策树,神经网络,遗传算法,关联规则挖掘算法
(3)数据挖掘分类:关联分析,序列模式分析,分类分析,聚类分析
四、计算机网络
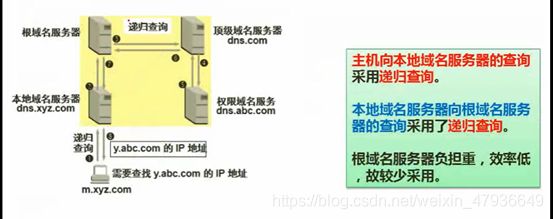
1.DNS协议
(1)递归查询:服务器必须回答目标IP与域名的映射关系。(一层一层查询)
(2)迭代查询:服务器收到一次迭代查询回复一次结果,这结果不一定是目标IP与域名的映射关系,也可以是其他DNS服务器的地址。(告诉你去哪查询,自己不参与)
方法一:常见形式
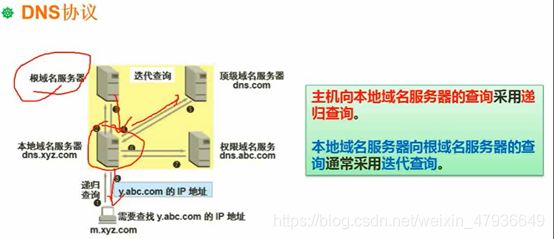
方法二:效率低
2.计算机网络的分类-拓扑结构
(1)按分布范围:局域网(LAN),城域网(MAN),广域网(WAN),因特网
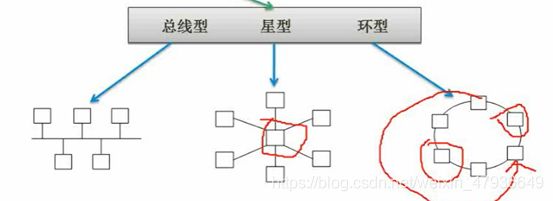
(2)按拓扑结构:总线型,星型,环形
3.网络规划与设计
(1)逻辑网络设计:

(2)物理设计:

分层设计(考各层职能较多):
核心层:容易出现数据冗余

4.子网划分
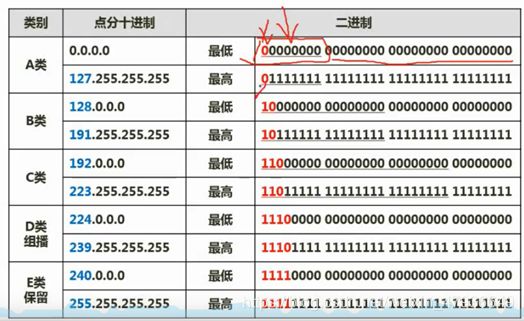
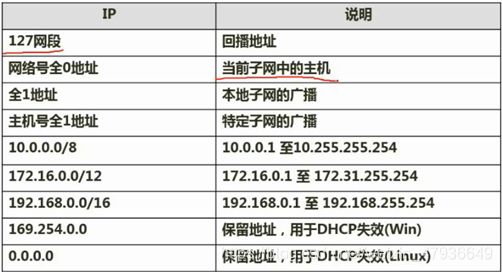
5.特殊含义的IP地址(选择题)
6.HTML(出现在选择题)
7.IPv6
8.信息系统安全属性
(1)保密性:最小授权原则、防暴露、信息加密、物理保密
(2)完整性:安全协议、校验码、密码校验、数字签名、公证
(3)可用性:综合保障(IP过滤、业务流控制、路由选择控制、审计跟踪)
不可抵赖性:数字签名
加密技术
(1)·对称加密技术

(2)非对称加密技术
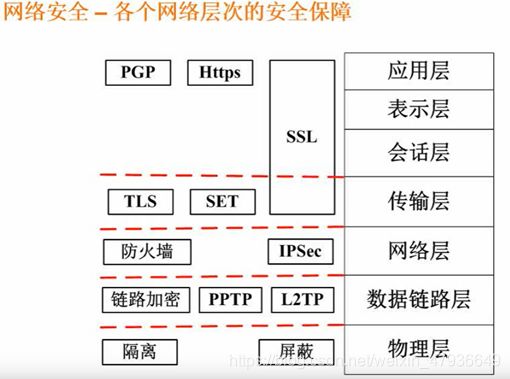
9.网络安全-各个网络层次的安全保障
五、数据结构与算法基础
1.数组存储地址计算
(1)一维数组a[n]:a[i]的存储地址:a+ilen
(2)二位数组a[m][n]:a[i][j]存储地址(按行存储):a+(in+j)len;a[i][j]按列存储:a+(jm+i)*len
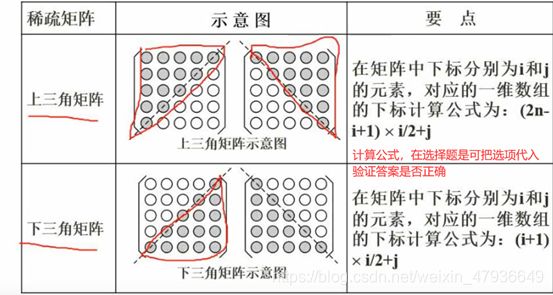
2.稀疏矩阵
3.线性表
(1)线性表可分:顺序表和链表
(2)链表又分:单链表,循环链表以及双向链表
顺序存储与链式存储对比
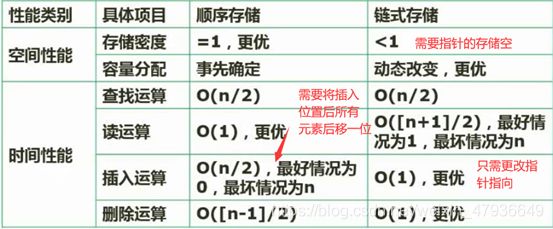
单链表的删除,插入结点操作:
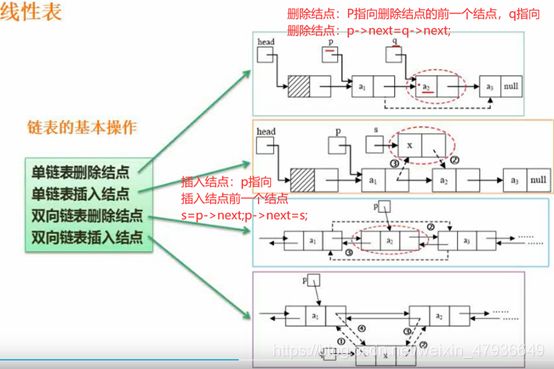
4.数与二叉树
1.二叉树的各种性质
(1)叶子结点数:结点个数n,总结点数=n+各度的结 点数相加
(2)数的性质:数的结点数为树中所有结点的度数之和再加1
(3)二叉树性质:度为0的结点数总是比度为2的结点数多1
(4)二叉树基本性质:深度为k的二叉树,最多有2^k-1个结点
(5)完全二叉树:度为1的结点个数为0或1
(6)满二叉树:深度为k的二叉树,最多有2^k-1
个结点,第k层的结点数2^(k-1)
(7)完全二叉树:具有2n个结点的完全二叉树中,叶子节点数为n
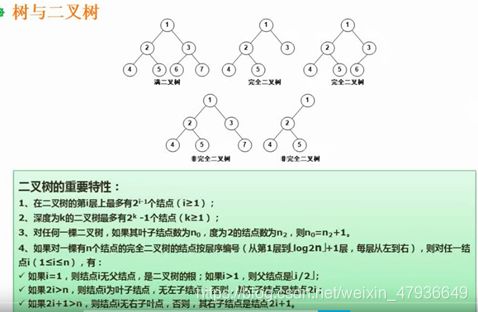
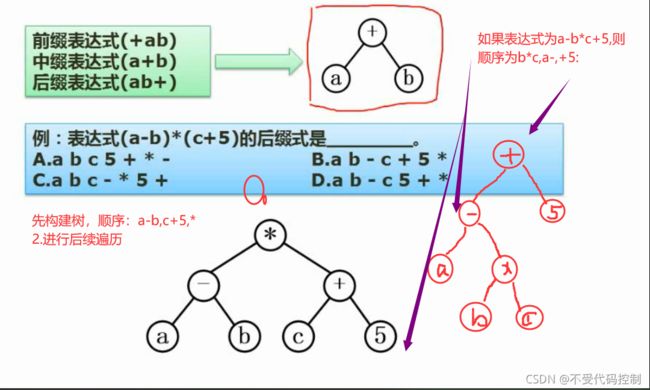
2.二叉树遍历
前序遍历:左右根
中序遍历:左根右
后序遍历:左右根
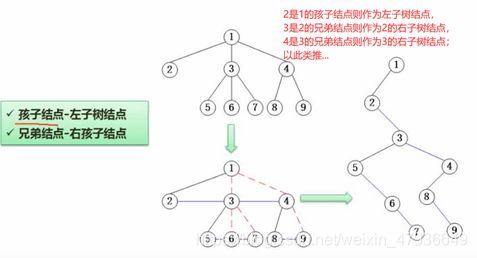
3.树转二叉树
3.查找(排序)二叉树
4.最优二叉树(哈夫曼树)
概念:数的路径长度:每根路经之和
权:叶子节点具有的权值
带权路径长度:叶子节点权值*路径长度
树的带权路径长度(树的代价):所有带权路径长度之和
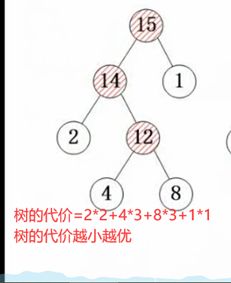
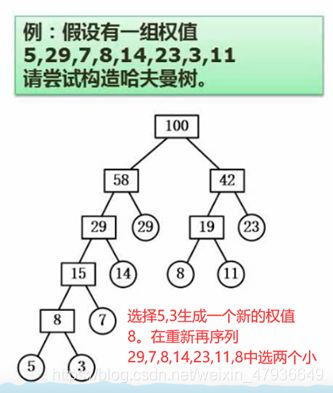
5.构造哈夫曼树
6.线索二叉树
左子树指向前(中,后)遍历的前驱节点,右子树指向前(中,后)遍历的后继节点
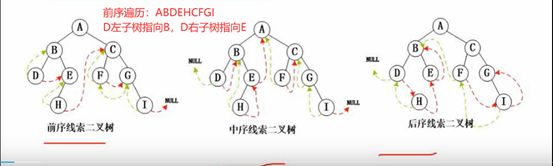
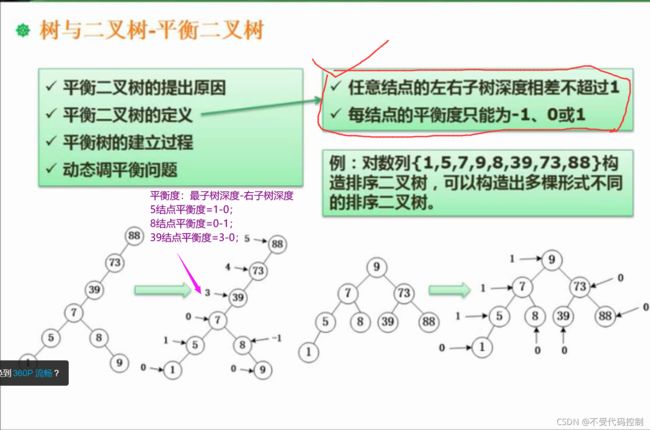
7.平衡二叉树
8.图
1.图的存储-邻接矩阵
无向图邻接矩阵特点:上三角与下三角对称,可以只存储半边节省空间;
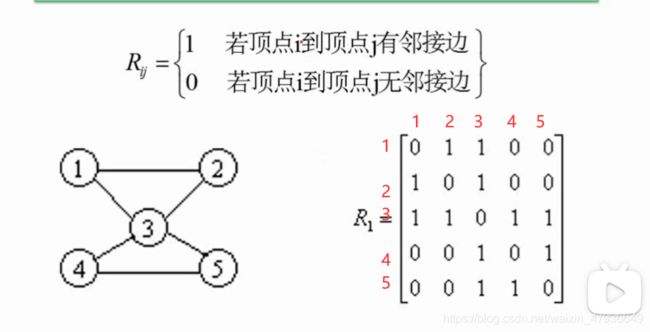
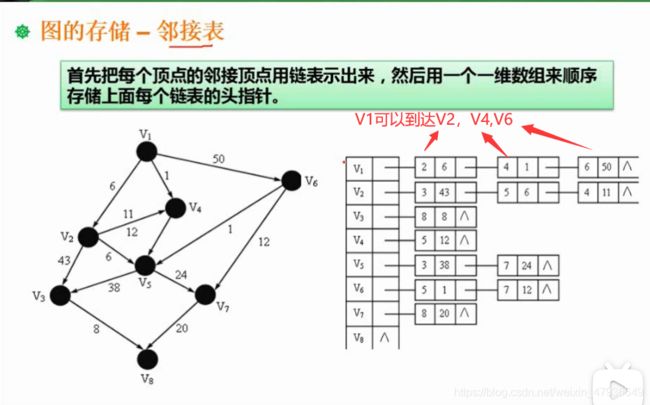
2.图的存储-邻接表
3.图-图的遍历
深度遍历与广度遍历的区别:
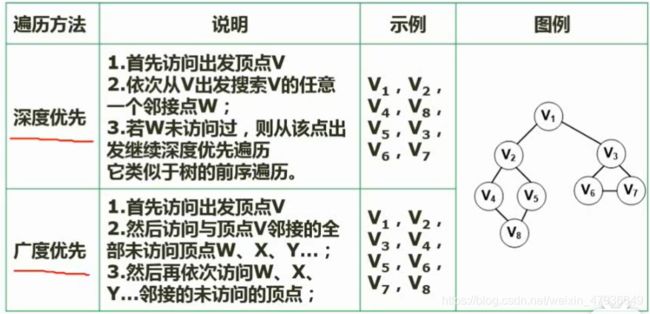
例子
深度遍历:V0,V4,V6,V7,V3,V1,V2,V5
广度遍历:V0,V4,V3,V1,V6,V2,V5,V7
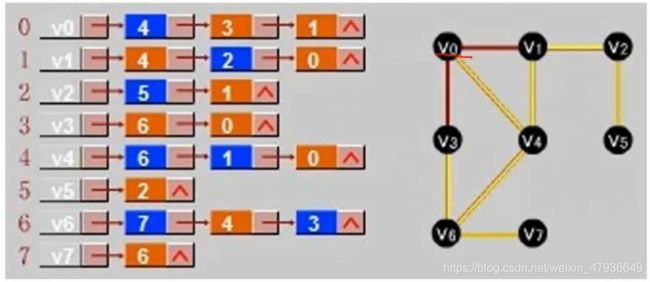
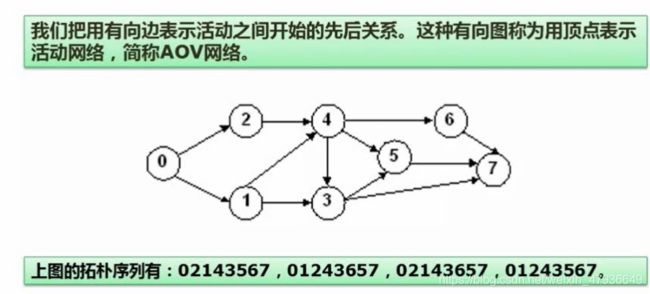
4.图-拓扑排序
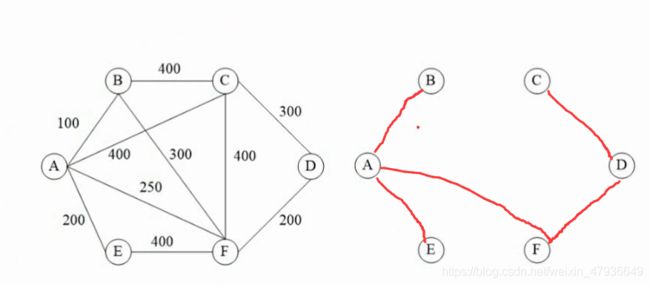
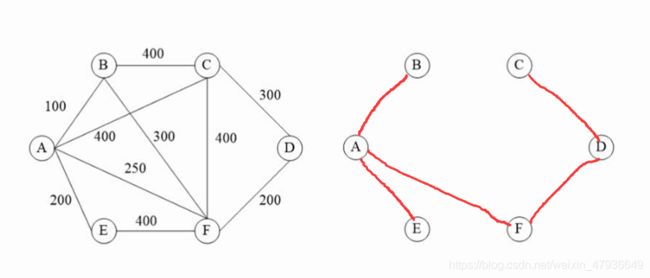
5.图的最小生成树-普利姆算法
方法:选出红点集到蓝点集权值最小且不能形成环路的路;红点与红点直接不能连接;
例子:1.选出A为红点集,A到其他蓝点集的权值中100最小且不形成环路则连接B;
2.A,B都为红点集,A,B到其他蓝点集权值最小且不形成环路的是E,则连接E;A,B,E都为红点集;
3.以此类推,直到无论连接哪条都形成环路为止;
5.图的最小生成树-克鲁斯卡尔算法
方法:直接选出5条权值最小且不能形成环路的路经;
9.算法的特性
10.算法的复杂度
时间复杂度与空间复杂度的定义
O(1):当只有一个语句时或者有限语句时;例:i=0;或者i=1;k=0;
O(n):例:一个for循环;当算法有几个复杂度是取值最高的复杂度;
O(n²):一个嵌套for循环;
O(log2(n)):在排序二叉树查询指定值,n为结点数,2是底数;

11.查找-顺序查找

时间复杂度
最好情况:执行一次;
最坏情况:执行n次;
平均查找长度:(1+n)/2
时间复杂度:O(n)
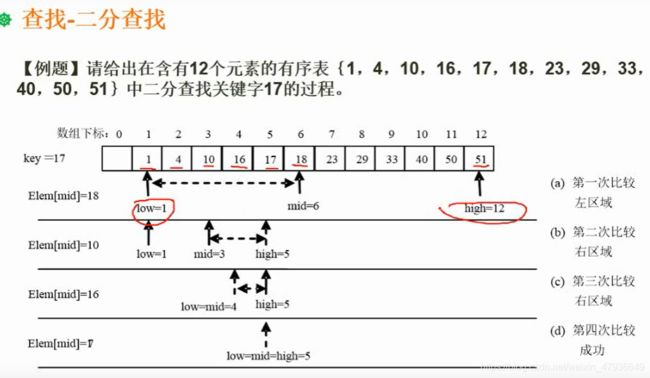
12.查找-二分查找
条件:排序数值是大到小或小到大的顺序
步骤:(1+12)/2取整=6,关键字与18比较确定查找范围【1,5】;
2.(1+5)/2取整=3,关键字与10比较确定查找范围【4,5】;
以此类推…
时间复杂度
比较最多次数:(log2(n))+1;2位底数,n位指数
时间复杂度:O(log2(n))
13.排序
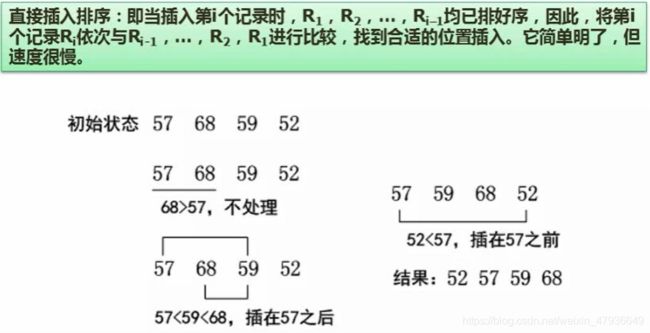
1.直接插入排序
2.希尔排序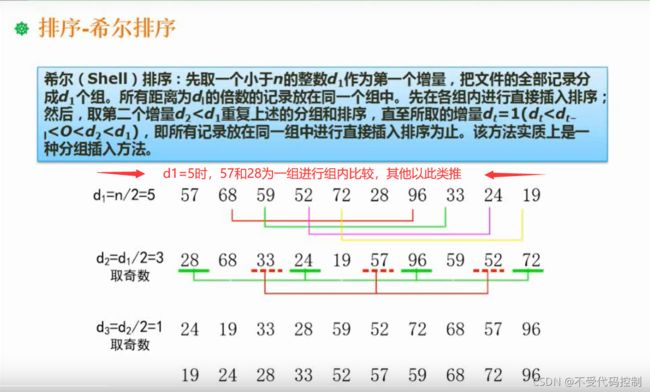
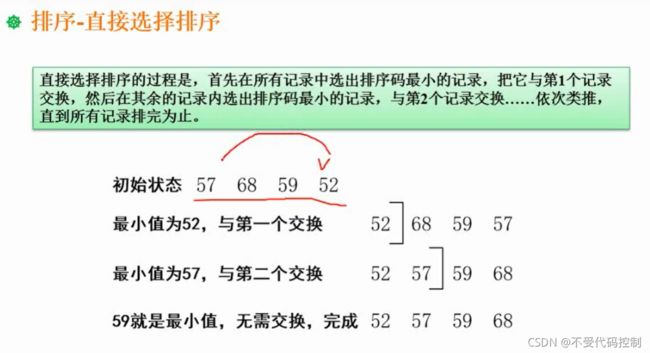
3.直接选择排序
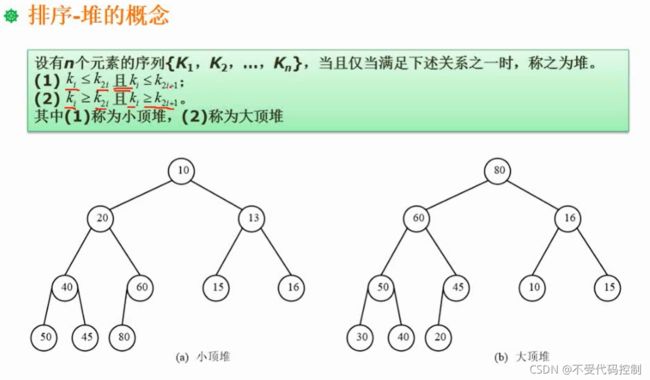
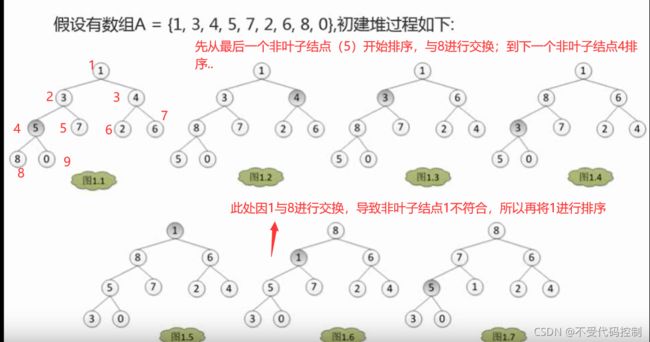
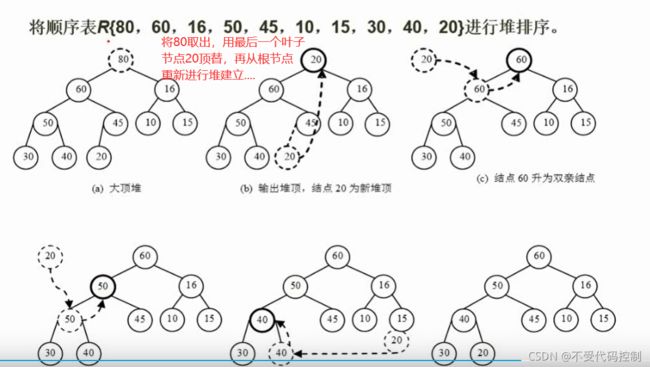
4.堆排序
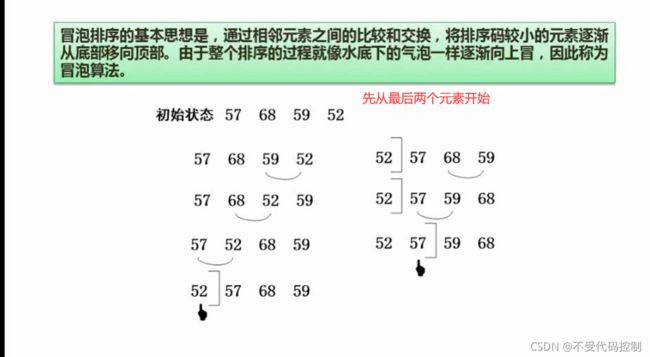
5.冒泡排序
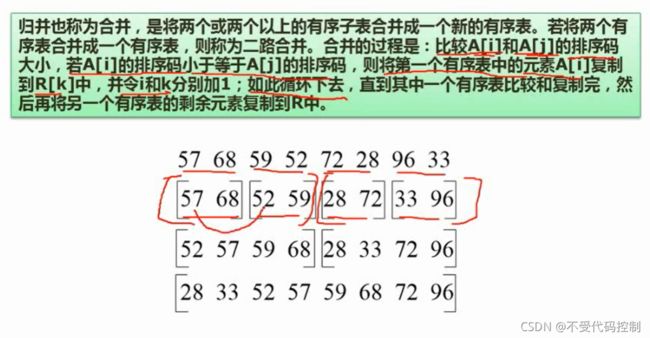
6.归并排序
7.快速排序
步骤:57为基准,与末端指针19进行比较,小于基准交换位置否则不变;
2.因57与19交换位置,基准变成最后一个元素,则将它与19的后一个元素比较;
以此类推。。
3.最后基准出现在中间,再将基准两边数进行排列;
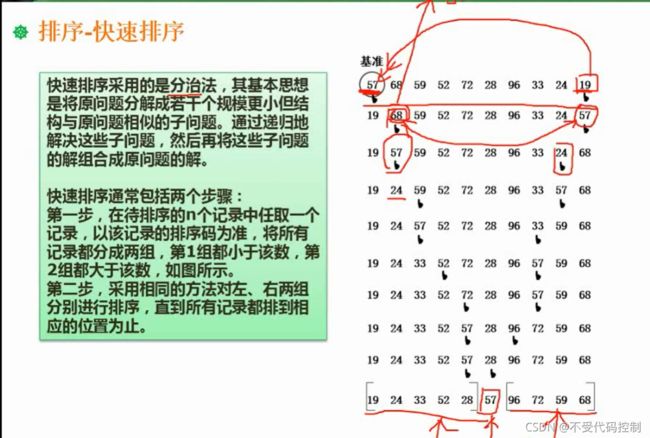
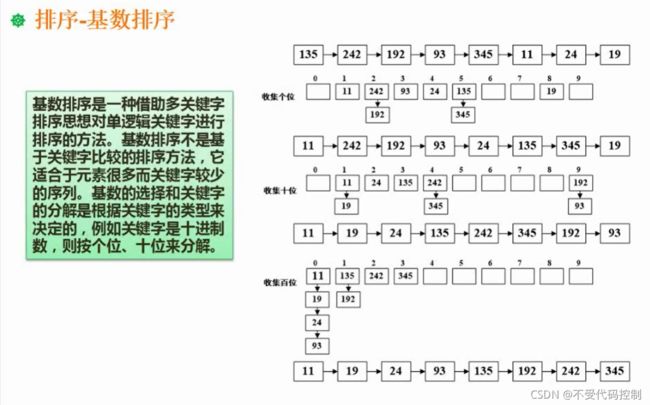
8.基数排序
14.时间复杂度和空间复杂度
8.程序设计与语言处理程序
1.文法

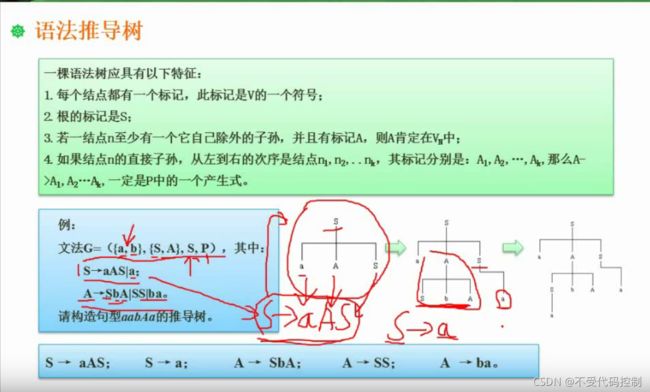
语法推导树
a,b:终结符(一般小写字母)
S,A:非终结符
S:起始符
P:产生式
**2.有限自动机与正规式
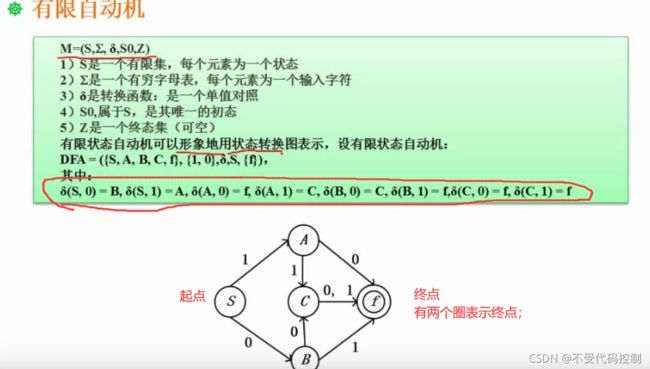
1.有限自动机
2.正规式
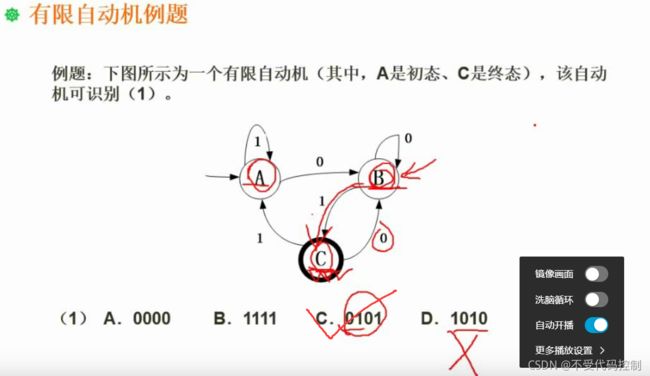
3.例题
3.表达式
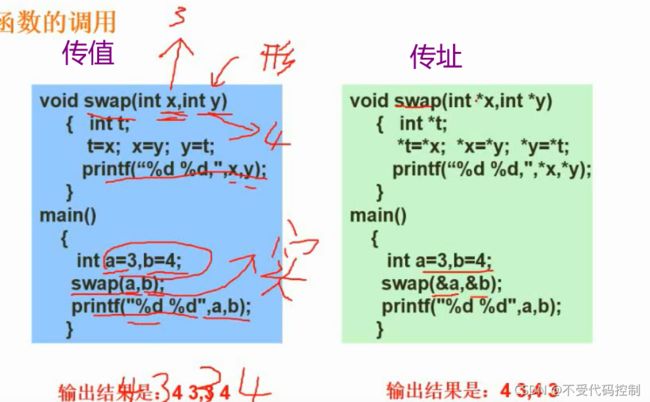
4.传值传址
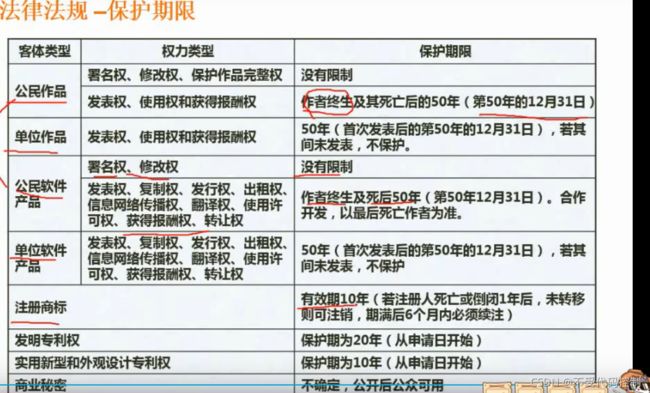
9.法律法规(3分左右)
1.保护权限
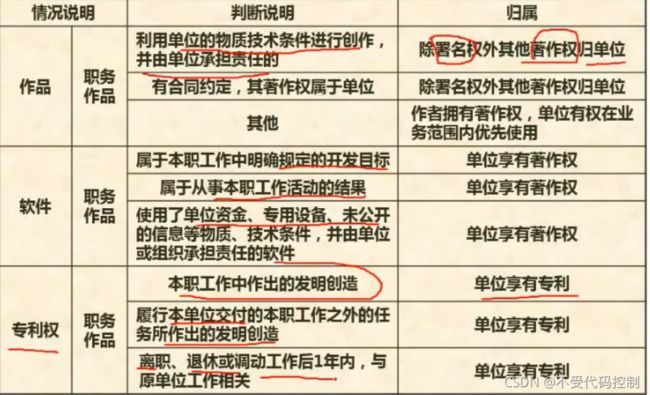
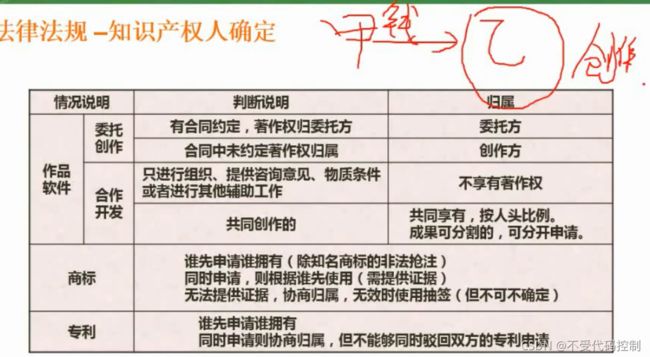
2.知识产权人确定
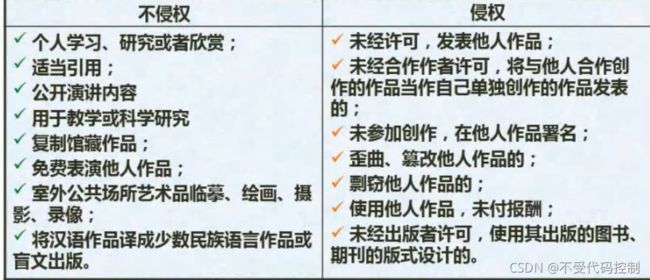
3.侵权判定(重点)
4.标准化基础知识-标准的编号
10.多媒体基础(1-3分)
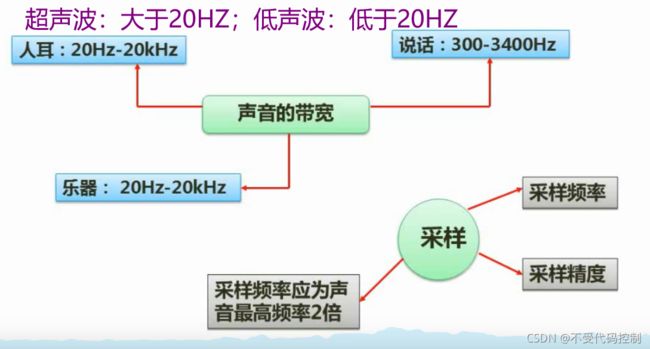
1.音频相关概念
2.图像相关概念
3.媒体的种类
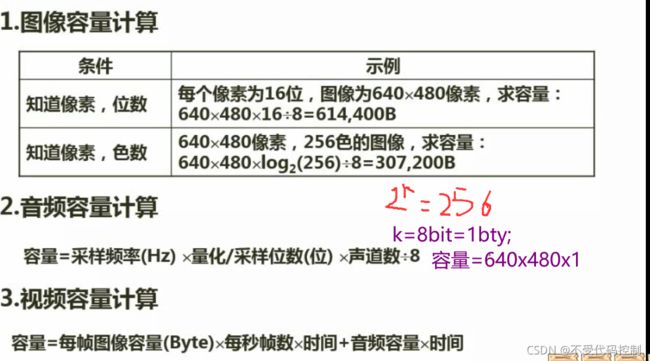
4.多媒体的相关计算
1.例题
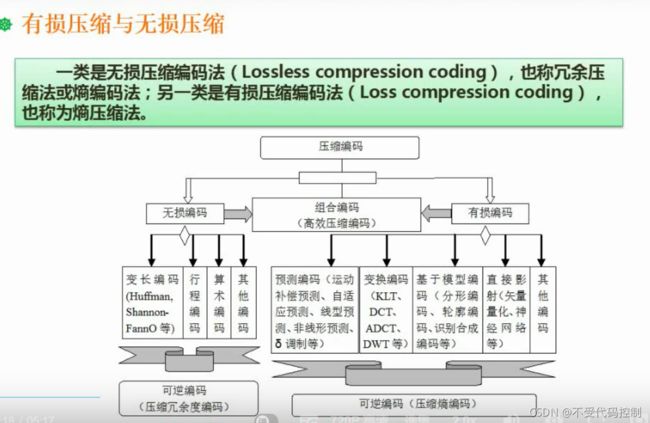
5.数据压缩
10.软件开发模型
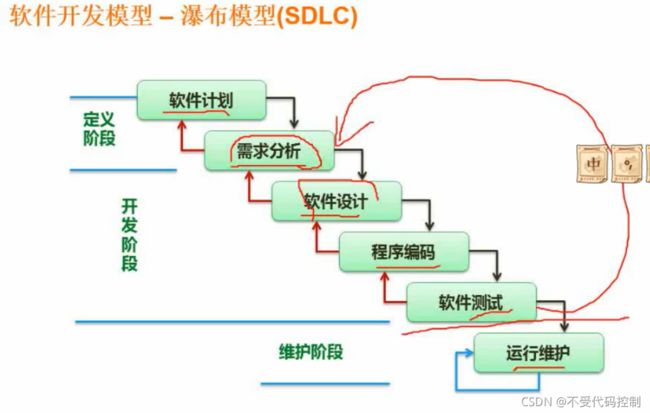
1.瀑布模型
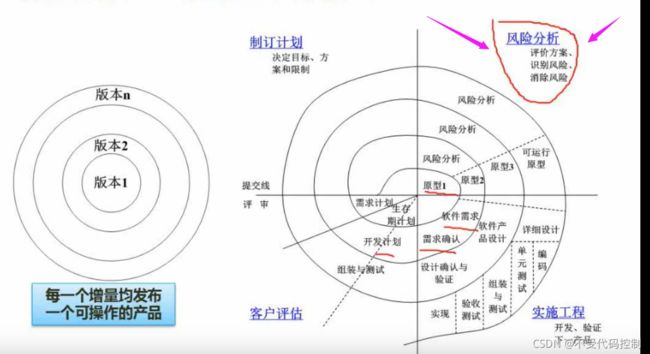
2.螺旋模型
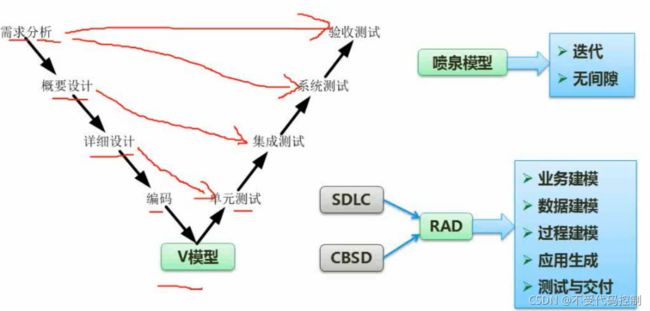
3.V型
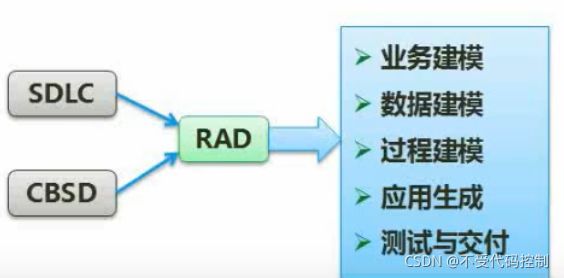
4.喷泉模型和RAD
5.构建组装模型CBSD
特点:提高复用性,缩短时间,成本变低, 提高可靠靠性
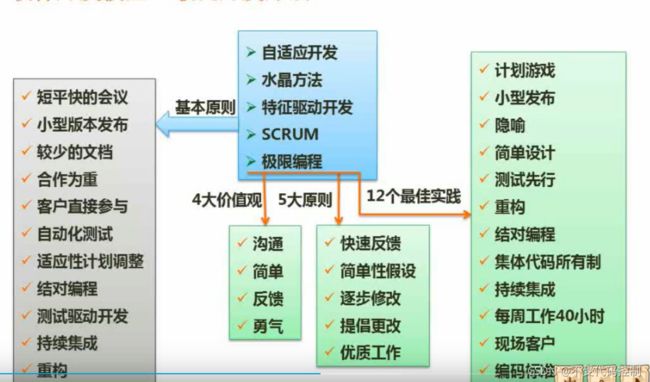
6.敏捷开发模型
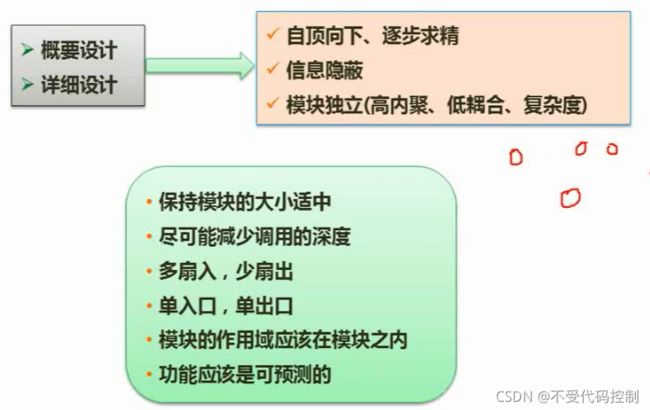
7.结构化设计
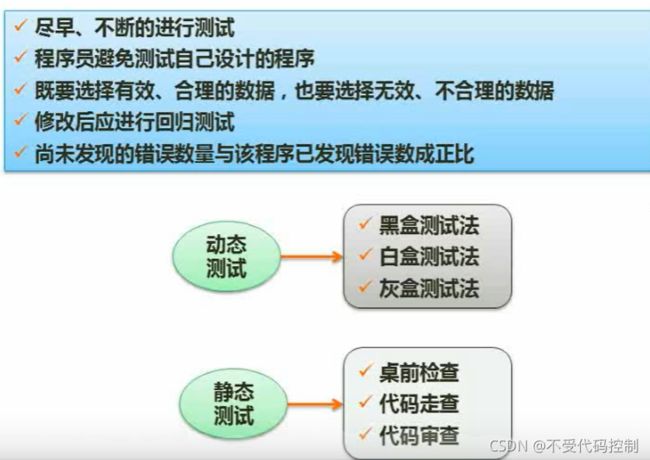
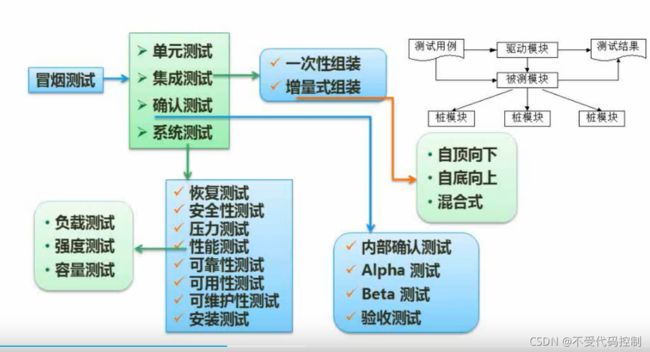
8.软件测试
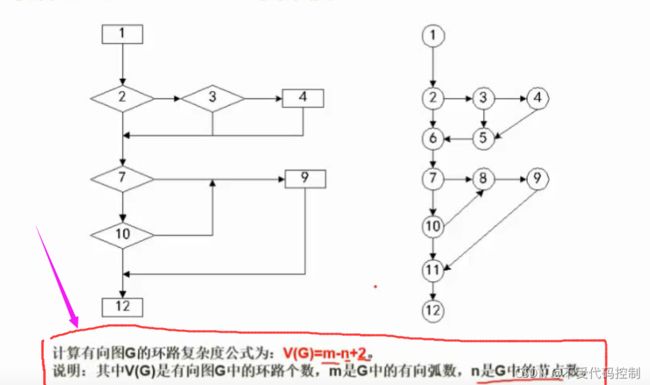
9.Macabe复杂度(必考)
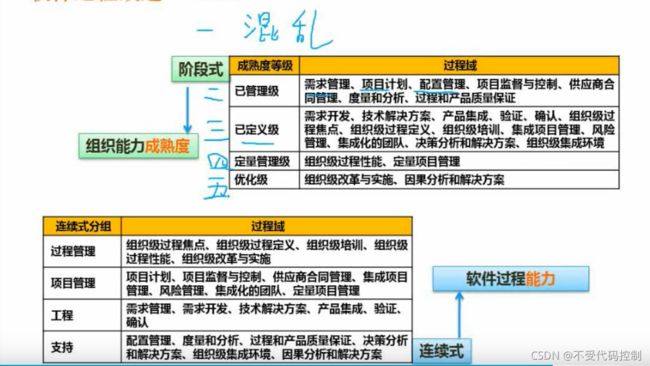
9.CMMI
10.项目管理
需重看一边视频
12.面向对象设计
1.设计原则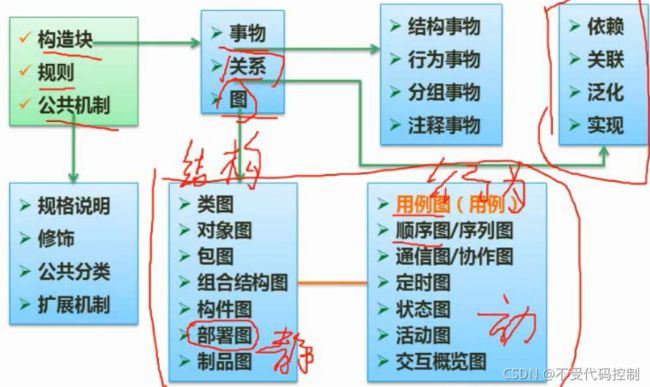
2.UML
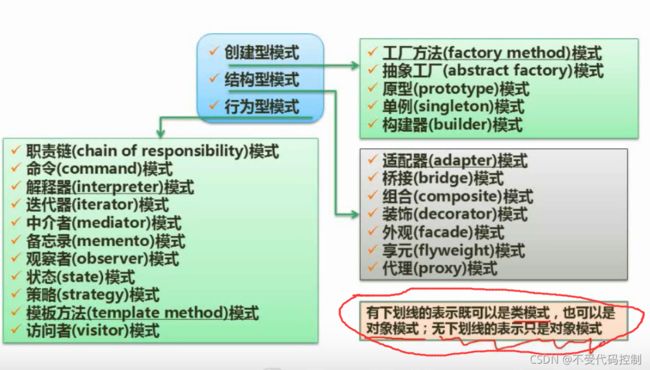
3.设计模式的分类
1.创建型模式
2.结构型模式
2.行为型模式
13.数据流图(重点,分值15分)
1.数字字典
2.数据流图平衡原则
14.数据库设计(15分)
需求分析(数据流图、数据字典、需求说明书)->概念结构设计(E-R模型)->逻辑结构设计(关系模式(通过E-R转换))->物理设计
15.UML
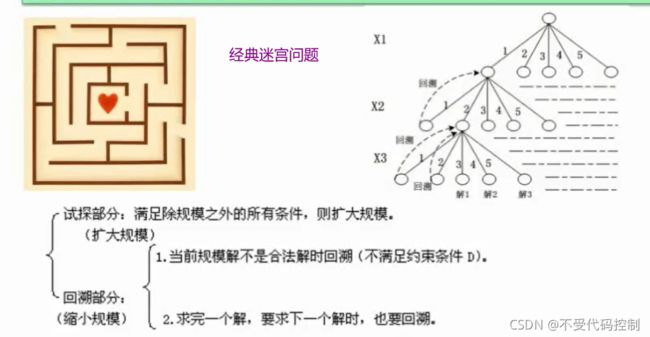
1.用例图
2.类图
主要考察方式:写类名,填多重关系,填关系
多重关系填写

填关系: 泛化,依赖,关联,实现
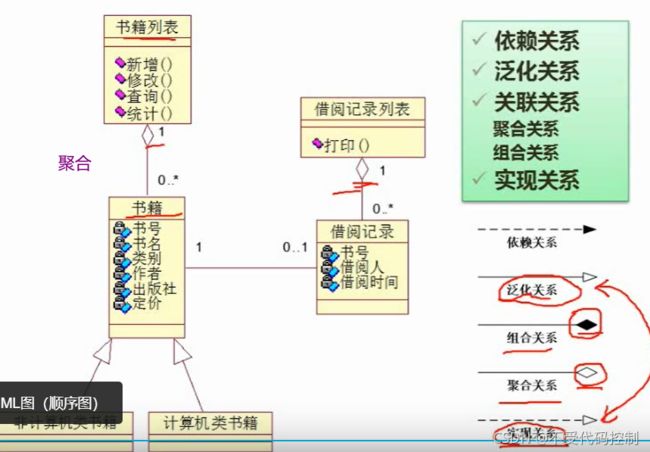
3.顺序图
考察方式:填消息,填对象名
4.活动图
16.数据结构与算法应用(下午题,较难)
1.分治法
利用递归解决问题
应用二分查找
2.回溯法
3.贪心法

笔记_第113张图片](http://img.e-com-net.com/image/info8/d86f60b7d76c44aa9ecb05bba5585e50.jpg)