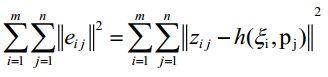SLAM | 视觉SLAM中的后端：后端优化算法与建图模板

点击上方“AI算法修炼营”，选择加星标或“置顶”

标题以下，全是干货

前面的话

前面系列一中我们介绍了，VSLAM 是利用多视图几何理论，根据相机拍摄的图像信息对相机进行定位并同时构建周围环境地图。按照相机的分类，有单目、双目、 RGBD、鱼眼、全景等。同时，VSLAM 主要包括视觉里程计（visual odometry， VO）、后端优化、回环检测、建图。

VSLAM 前端为视觉里程计和回环检测，相当于是对图像数据进行关联；后端是对前端输出的结果进行优化，利用滤波或非线性优化理论，得到最优的位姿估计和全局一致性地图。

前面已经介绍了VSLAM的前端：视觉里程计和回环检测，这次我们将介绍系列二：VSLAM中的后端优化和建图。

接下来，我们将详细介绍。

2 后端：最优化位姿估计和全局一致性地图

2.1 后端优化

SLAM 的后端求解方法可大致分为两大类，一类是基于滤波器的方法；另一类则是非线性优化方法。这是根据假设的不同，如果假设马尔可夫性， K 时刻状态只与 K-1 时刻状态有关，而与之前的状态无关，这样会得到以扩展卡尔曼滤波（EKF）为代表的滤波器方法。在滤波方法中， 本文会从某时刻的状态估计推导到下一个时刻。另外一种方法是考虑K 时刻与之前所有状态的关系，这将得到非线性优化为主体的优化框架。

2.1.1 滤波方法

由于SLAM 本质上是一个状态估计问题，该问题可以归结为一个运动方程和一个观测方程，顺理成章地把 SLAM 融入到滤波框架中。早期的 SLAM 研究基本都是在滤波器的框架下。在假定从 0 到 t 时刻的观测信息以及控制信息已知的条件下，对系统状态的后验概率进行估计，根据后验概率表示方式的不同，存在多种基于滤波器的方法，如扩展卡尔曼滤波（EKF）方法、粒子滤波（PF）等。 

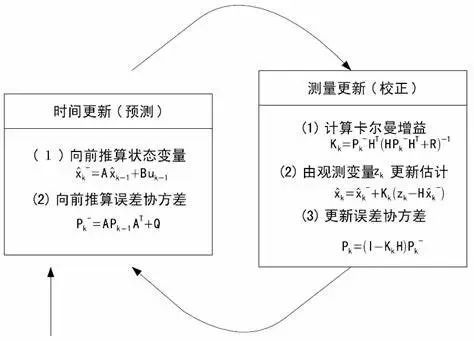
1．卡尔曼滤波（KF）

Kalman滤波算法的本质就是利用两个正态分布的融合仍是正态分布这一特性进行迭代而已。

步骤一：用上一次的最优状态估计和最优误差估计去计算这一次的先验状态估计和先验误差估计。

（最优估计就是“最准确的估计（其实就是已经经过卡尔曼滤波之后的数据）”，先验估计就是“粗略的估计”（其实就是还没经过卡尔曼滤波之后的数据））。

 

步骤二：用步骤一得到的本次先验误差估计和测量噪声，得到卡尔曼增益。

（卡尔曼增益用于把“粗略的估计”变成“最准确的估计”。至于为什么先验误差和测量噪声可以得到卡尔曼增益，道理很简单，你想想看，先验误差代表了数学模型的误差，测量噪声代表了传感器的误差，根据两个误差的大小来决定加权的权值，是不是一点毛病都没有？就好比数学模型误差是1，传感器测量误差是100，那我就选择99%相信数学模型，1%相信传感器。）

步骤三：用步骤一、步骤二得到的所有先验估计和卡尔曼增益得到本次的最优估计。

（你看，这就是一个循环了，然后第四步就是第一步，用本次的最优估计算下一次的先验估计。）

2．扩展卡尔曼滤波（EKF）

 

扩展卡尔曼滤波将非线性的运动方程和观测方程进行以切线代替的方式来线性化。其实就是在均值处进行一阶泰勒展开。

EKF两个重要的影响因素，局部非线性化程度和原始不确定度，在实际使用时要注意尽量减小这两者的影响以获得较好的估计结果。

对非线性问题采用一阶泰勒展开存在着两个缺点，其一是当强非线性时 EKF 违背局部线性假设，Taylor 展开式中被忽略的高阶项带来大的误差时，EKF 算法可能会使滤波发散；另外，由于 EKF 在线性化处理时需要用雅克比 (Jacobian) 矩阵，其繁琐的计算过程导致该方法实现相对困难。所以，在满足线性系统、高斯白噪声、所有随机变量服从高斯 (Gaussian) 分布这 3 个假设条件时，EKF 是最小方差准则下的次优滤波器，其性能依赖于局部非线性度。

3. 无迹卡尔曼滤波（UKF）

无迹卡尔曼滤波是无损变换 (UT) 和标准 Kalman 滤波体系的结合，通过无损变换使非线性系统方程适用于线性假设下的标准 Kalman 滤波体系。

UKF 以 UT 变换为基础，摒弃了对非线性函数进行线性化的传统做法，采用卡尔曼线性滤波框架，对于一步预测方程，使用无迹 (UT) 变换来处理均值和协方差的非线性传递，就成为 UKF 算法。UKF 是对非线性函数的概率密度分布进行近似，用一系列确定样本来逼近状态的后验概率密度，而不是对非线性函数进行近似，不需要求导计算 Jacobian 矩阵。UKF 没有线性化忽略高阶项，因此非线性分布统计量的计算精度较高。

4. 粒子滤波（PF）

粒子滤波器(particle filter)是一种使用蒙特卡罗方法(Monte Carlo method)的递归滤波器，透过一组具有权重的随机样本(称为粒子)来表示随机事件的后验几率，从含有噪声或不完整的观测序列，估计出动态系统的状态，粒子滤波器可以运用在任何状态空间的模型上。

粒子滤波器是卡尔曼滤波器(Kalman filter)的一般化方法，卡尔曼滤波器建立在线性的状态空间和高斯分布的噪声上；而粒子滤波器的状态空间模型可以是非线性，且噪声分布可以是任何型式。

步骤

• 步骤1：生成粒子：为了估计机器人真实位置，我们选取机器人位置x,y和其朝向θ作为状态变量，因此每个粒子需要有三个特征。

• 步骤2：利用系统模型预测状态：每一个粒子都代表了一个机器人的可能位置，假设我们发送控制指令让机器人移动0.1米,转动0.7弧度，那么可以让每个粒子移动相同的量。由于控制系统存在噪声，因此需要添加合理的噪声。 

• 步骤3：更新粒子权值：使用测量数据(机器人距每个路标的距离)来修正每个粒子的权值，保证与真实位置越接近的粒子获得的权值越大。由于机器人真实位置是不可测的，可以看作一个随机变量。根据贝叶斯公式可以称机器人在位置x处的概率P(x)为先验分布密度(prior)，或预测值，预测过程是利用系统模型(状态方程)预测状态的先验概率密度，也就是通过已有的先验知识对未来的状态进行猜测。在位置x处获得观测量z的概率P(z|x)为似然函数(likelihood)。后验概率为P(x|z)， 即根据观测值z来推断机器人的状态x。更新过程利用最新的测量值对先验概率密度进行修正，得到后验概率密度，也就是对之前的猜测进行修正。

• 步骤4：重采样：在计算过程中，经过数次迭代，只有少数粒子的权值较大，其余粒子的权值可以忽略不计，粒子权值的方差随着时间增大，状态空间中的有效粒子数目减少，这一问题称为权值退化问题。随着无效粒子数目的增加，大量计算浪费在几乎不起作用的粒子上，使得估计性能下降。

  重采样方法舍弃权值较小的粒子，代之以权值较大的粒子，有点类似于遗传算法中的“适者生存”原理。重采样的方法包括多项式重采样(Multinomial resampling)、残差重采样(Residual resampling)、分层重采样(Stratified resampling)和系统重采样(Systematic resampling)等。重采样带来的新问题是，权值越大的粒子子代越多，相反则子代越少甚至无子代。这样重采样后的粒子群多样性减弱，从而不足以用来近似表征后验密度。克服这一问题的方法有多种，最简单的就是直接增加足够多的粒子，但这常会导致运算量的急剧膨胀。

• 步骤5：计算状态变量估计值：系统状态变量估计值可以通过粒子群的加权平均值计算出来。

5. 总结

KF针对线性高斯的情况

EKF针对于非线性高斯，其是将非线性部分进行一阶泰勒展开，因此忽略了高阶项，误差较大

UKF是将UT变换与KF结合的产物。可以说，EKF和UKF是针对同一问题的不同思路的解决方案，其实UKF能力已经跳出了非线性高斯的范围，也可以解决非高斯问题，只不过在这方面PF能做的更好，运算量也更大。

滤波方法在VSLAM中的局限

1、随着SLAM问题研究的深入及其应用逐步从小场景转向大场景，基于滤波的SLAM方法越来越受到局限。比如EKF方法需要把路标放进状态，由于VSLAM中路标数量很大，而且存储的状态量呈平方增长（协方差矩阵），所以EKFSLAM被普遍认为不适合大场景。

2、滤波方法假设马尔可夫性，假设当前状态只与上一时刻相关，而与之前状态和观测都无关，这种处理方式是的滤波器很难处理回环问题。而基于非线性优化方法倾向于使用所有的历史数据，称为全体 SLAM（full SLAM）。从某种程度上说，非线性优化使用了更多的信息，当然能获得更好的建图效果。

1.1.2 非线性优化方法

代价函数的建立

在 VSLAM 中，如果不考虑运动方程，假设观测误差： ，其中 h（）为观测方程，ξ 为外参 R，t 对应的李代数，三维点P是路标，k是像素坐标

如 果 考 虑 所 有 的 观 测 量 ， 那 么 整 体 的 代 价 函 数 为：

对这个函数采用最小二乘求解，相当于对所有相机位姿和路标同时调整，使目标函数最小，这就是 bundle adjustment （BA）。

过去，研究者普遍认为非线性优化方法计算量非常大，不适合实时计算；直到最近十年，SLAM 问题中 BA 的稀疏特性才逐渐被认识到，才使它能够在实时的场景中应用 。

对上式 BA 的求解，无论是采用高斯牛顿还是列文伯格—马夸尔特（LM）方法，最后都将面临增量方程：。

以高斯牛顿为例， H 矩阵为 ，由于雅可比矩阵 J 包含了所有的路标点，尤其是 VSLAM 中，一幅图像至少会提取数百个特征点，如果直接对 H 求逆（复杂度为 O（n3）），计算量非常大。 

矩阵 H 的稀疏结构

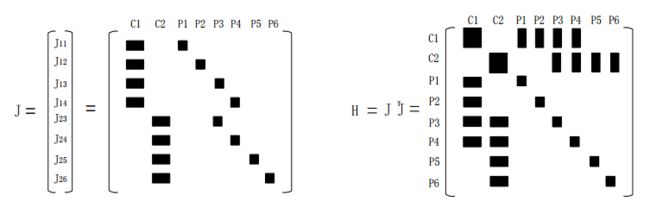
假设场景中有两个相机位姿（a1，a2） 和六个路标（b1， …， b6），a1 观测到路标 b1、b2、 b3、 b4， a2 观测到路标 b3、b4、 b5、 b6，则雅可比 J为 8*8 的矩阵（两个相机位姿加六个路标）。

误差残差 e11表示在 a1 看到了b1，与其他的相机位姿和路标无关， J11 为e11 所对应的雅可比矩阵， 从而得到如下图 （a）所示的雅可比形式， 再进一步得到如下图 （b）所示的矩阵 H（H 的稀疏性是由 J 引起的）。

因为 VSLAM 中路标数量至少也有数百个，所以矩阵 H 的右下角是一个维数很大的对角块矩阵，该对角块求逆难度远小于对矩阵 H 的求逆难度。鉴于此，对BA 的求解都是采用 Schur 消元（也称做边缘化），具体 BA的算法一般采用 G2O或 Ceres库实现。

随着计算机性能的进步， 以及逐渐认识到 VSLAM 中雅可比矩阵的稀疏特性，现在主流的 VSLAM 都是采用非线性优化的方法，使用 G2O 等库来求解 BA。VSLAM 的后端仅仅出现过一个基于滤波器的 MonoSLAM，之后都是非线性优化统一了后端：一是 EKF 需要对地图和相机位置进行更新，但是 VSLAM 中路标的数量动辄成百上千，存储的状态量呈平方增长，所以 EKF 被普遍认为不适合大的场景，而优化方法没有这样的限制；还有非线性优化可以利用历史所有数据，这和回环检测的模型是相关的，而 EKF 很难做回环检测。

2.2 建图

地图的具体形式主要有路标地图、拓扑地图、度量地图和混合地图。

• 路标地图，由一堆路标点组成，在早期的基于 EKF 的SLAM 中比较常见。
  

• 拓扑地图强调地图元素之间的连通关系，由节点和边组成，只考虑节点间的连通性， 而对精确的位置要求不高，去掉了大量地图的细节，是一种比较紧凑的地图表达方式。

• 度量地图分为栅格地图和几何地图。栅格地图将整个环境分为若干个大小相同的栅格，每个栅格代表环境的一部分。二维栅格地图在以激光雷达为传感器的扫地机器人里十分常见，它只需用 0-1 表示某个点是否有障碍，对导航很有用，而且精度也比较高， 但是它比较占存储空间，尤其是三维栅格地图，它需要把所有的空间点都存起来。几何地图通过收集对环境的感知信息，从中提取几何特征（如点、线、面）描述环境， 多见于早期的 SLAM 算法中。

• 混合地图通常采用分层结构将多种地图组合， 如拓扑地图和度量地图组成的混合地图， 上层的拓扑地图实现粗略的全局路径规划，底层的度量地图实现精确的定位和路径的优化。
  

在 VSLAM 中广泛应用的是度量地图, 它精确地表示地图中物体的位置关系， 可按稀疏和稠密划分。特征点法得到稀疏点云地图，直接法得到半稠密或稠密地图。针对稠密的度量地图， 当查询某个空间位置时，地图能够给出该位置是否可以通过的信息。

VSLAM 中建图的基本原理是通过三角测量或深度估计，将 2D 图像中的信息转换为空间 3D 路标点。在 VSLAM 中建图过程和位姿估计过程是同时完成的。 

深度估计在建图模块中占据非常重要的地位， 通常在VSLAM 系统中都有专门的线程对其进行处理。 SVO 采用高斯加上均匀分布的方法估计三维空间点的深度信息，并不断更新，直到其收敛。在 LSDSLAM 中，针对关键帧，通过之前关键帧的点投影初始化当前帧的深度估计；针对非关键帧，通过卡尔曼滤波不断地利用观测值对深度进行修正。 

结语

该篇作为SLAM系列的第二篇，主要介绍了视觉SLAM系统后端优化与建图模块。接下来，SLAM系列文章会持续更新，会继续和大家介绍视觉SLAM的主流框架，VIO多传感器融合以及激光SLAM等内容，欢迎大家持续关注~

获取文中思维导图完整版，请关注公众号留言或扫描下方个人微信。

参考：

1.视觉十四讲 高翔

2.https://www.cnblogs.com/21207-iHome/p/5237701.html

3.https://blog.csdn.net/young_gy/article/details/78468153

推荐阅读

目标检测系列

• 秘籍一：模型加速之轻量化网络

• 秘籍二：非极大值抑制及回归损失优化

• 秘籍三：多尺度检测

• 秘籍四：数据增强

• 秘籍五：解决样本不均衡问题

• 秘籍六：Anchor-Free

语义分割系列

• 一篇看完就懂的语义分割综述

面试求职系列

• 决战春招！算法工程师面试问题及资料超详细合集

一起学C++系列

• 内存分区模型、引用、函数重载

竞赛与工程项目分享系列

• 如何让笨重的深度学习模型在移动设备上跑起来

• 基于Pytorch的YOLO目标检测项目工程大合集

SLAM系列

• 视觉SLAM前端：视觉里程计和回环检测
  

-END-

扫描个人微信号，

拉你进AI算法修炼营学习交友群。

目标检测、图像分割、自动驾驶、机器人、面试经验

福利满满，名额已不多…

▲长按关注我们

觉得好看对你有帮助，就点个在看吧