软考-中级-网络工程师-笔记-第2章-数据通信基础

软考-中级-网络工程师-笔记-第1章-计算机网络概论

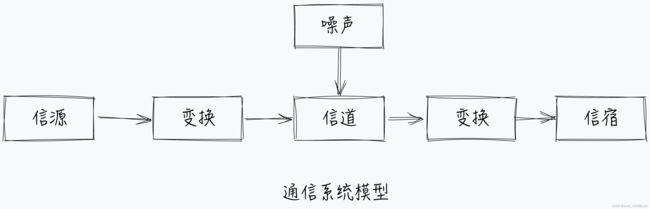
第2章 数据通信基础

2.1 数据通信的基础概念

模拟信号-连续的

数字型号-离散到

来奎斯特

香农定理

2.2 信道特性

2.2.1 信道带宽

信道带宽（W）

模拟信道：带宽 $W=f2-f1$（信道能通过最高/最低评率，单位赫兹Hz）

数字信道：数字信道时离散信道。带宽为信道能够达到的最大传输速率，单位是bit/s

B=byte=8bit

数据传输速率

指每秒能够传输的二进制数据位数。单位为比特/秒（bit/s或者b/s或者bps）

码元：一个数字脉冲称为一个码元（可以理解为时钟周期的信号）

码元速率：单位时间内信道传送码元的个数。如果码元宽度（脉冲周期）为T，则码元速率（波特率）为B=1/T，单位是波特（Baud）

一个码元携带信息量为n（位）与码元种类书（N）的关系$n={\log }_{2}N$

尼奎斯特定理：在一个理想的（没有噪声环境）信道中，若信道带宽为W，最大码元速率为： $B=2W（Baud）$

极限数据速率$R=B{\log }_{2}N=2W{\log }_{2}N$

每秒包裹总重=每秒发送包裹个数*每个包裹重量（码元速率*每个码元写到的信息量）

香农定理 ：在一个噪声信道的极限速率和带宽之间的关系

极限速率公式： $C=W{\log }_2(1+S/N)$

分贝与信噪比关系： $dB=10{\log }_{10}S/N$

其中W为带宽，S为信号平均功率，N为噪声平均功率。S/N为信噪比。

带宽20M 信噪比 1 求极限带宽

$C=20{\log }_{2}1$

2.2.3 信道延迟

误码率是传输出错的码元数占传输总码元数的比例

误码率一般小于$10^{-6}$

网络性能参数：

• 数据延时 < 200ms
• 语音视屏延时 < 50ms
• 抖动 < 20ms
• 丢包率 < 1%

信道延迟：

发送数据时间=线路延迟+调制研制

线路延迟=传输距离/传输速度（路上的时间）

调制延迟=数据帧大小/速率（排队上车的时间）

光速=300000km/s

电缆速度=200000km/s

卫星信道的时延大约是270ms（双向的延迟）

2.3 传输介质

2.3.1 双绞线

8根铜线每两根扭在一起，百兆用4根-1246，千兆必须用8根

分类：直通线/交叉线，屏蔽和非屏蔽

2.3.2 同轴电缆

2.3.3 光缆

利用光在玻璃或者塑料纤维中全反射原理达成的光传到工具

光传导损耗比电缆传导消耗低，距离长

特点： 重量轻、体积小、传输远、容量大、抗电磁干扰

光线分类：

单模光纤：一种模式在其中传播。大容量、长距离传输（贵）

多模光纤：容量小距离短，允许多种模式光信号传播

2.3.4 无线通信

无线信道包括微波、红外和短波信道，

2.4 数据编码

1. 单极性码

用正的（或者负的）电压表示数据。高电压表示1，0点压表示0

2. 极性码

分别用正负电压表示二进制0和1

3. 双极性码

交替反转编码（AMI）0电平表示0 1则在正负之间交替反转 1跳0不跳

4. 归零码（RZ）

码元中间的信号回归到0电平，

从负到0表示1 从正到0表示0

5. 不归零码（NRZ）

出现1电平翻转，出现0电平不反转-差分码 1跳0不跳

6. 双相码

一高一低必须翻转，具有自定时和检测错误的功能

7. 曼切斯特编码

自定义 低到高为1 高到低为0

8. 差分曼切斯特编码

有变化为0 无变化为1 （有0无1）

两种曼切斯特编码的特点：

• 优点：将时钟和数据包含在信号数据流中，也成自同步码
• 编码效率低
• 编码效率都是50%，一般用于最早的10M以太网编码

9. 多电平编码

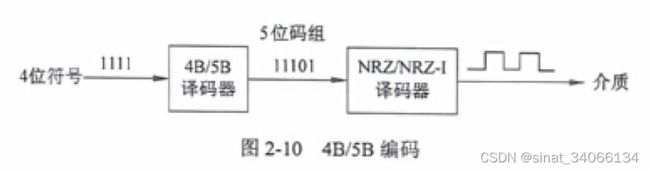
10. 4B/5B编码

发送数据流每4bits。使用不归零码（NRZ- I）编码成5bit。多一位用于解决同步问题。

编码效率：

曼切斯特和差分曼切四特50%

4B/5B效率80% 用于百兆以太网

8B/10B效率80%。用于前兆以太网

64B/66B效率97%，用于万兆以太网

2.5 数字调制技术

数字信号转换成模拟信号为调制，模拟信号转换为数字信号为解调

1. 幅度健控（ASK）：用载波的两个不同振幅表示0和1
2. 频移键控（FSK）：用载波的两个不同频率表示0和1
3. 相移键控（PSK）：用载波的的起始相位的变化表示0和1
4. 正交幅度调制（QAM）：把两个幅度相同但相位差90度的模拟信号合成一个模拟信号

2.6 脉冲编码调制

解调： 把模拟信号转换成数字信号的过程

脉码调制：PCM

PCM数字化过程3个步骤：采样、量化、编码

2.6.1 取样

按照一定的时间间隔对模拟信号进行取样，把模拟信号的当前值当作样本。

奈奎斯特取样定理：如果取样速率大千模拟信号最高频率的两倍，则可以用得到的样本空间恢复原来的模拟信号，即
$$f=\frac{1}{T}>2f_{max}$$
其中：f为取样频率，T为取样周期。$f_{max}$为信号的最高频率。

2.6.2 量化

把取样后得到的样本由连续值转化为离散值，离散值的个数决定了量化的精度

量化等级N

$n={\log }_{2}N$

2.6.3 编码

编码：把量化后的样本变成相应的二机制代码。可以得到相应的二进制代码序列。其中每个二进制代码都可以用一个脉冲串来表示，这一组脉冲序列就表示了经PCM编码的模拟信号。

例如：对声音信号数字化，声音最高频率是4kHz，采样频率为8kHz，对语音样本用128个等级量化，因而每个样本用7bit表示，在数字信道上传输着用数字化后的语音信号的速率是7*8000=56Kbps.
$$
N=128 \

n=log_2N=7
$$

2.7 通信方式和交换方式

2.7.1 数据通信方式

1. 通信方向

单工通信

信息智能在一个方向传输，发送方不能接受，接收方不能发送（电视/广播）

半双工通信

通信的双方可以交替进行发送和接受消息，但不能同时接受或发送（对讲机/WIFI/HUB）

双工通信

通信双方可以同时进行双向的信息发送（电话/交换机）

2. 同步方向

异步传输

​ 把各个字符分开传输，在字符串之间插入一位起始位（0），在自负之后插入一位停止为（1），起始位度i接收方的时钟气质为，在自负和停止位之间加入一个校验位，一般使用奇偶校验

同步传输

比特分组（帧）要大，

2.7.2 交换方式

1. 电路交换
   将数据传输分为电路建立、数据传输和电路拆除3个过程，在数据传输之前需要建立一条物理链路，在线路被释放之前、该同路将一直被用户完全占有（电话）
2. 报文交换
   报文从发送方传送到接收方采用存储转发的方式。报文中含有每一个吓一跳节点，完整的报文在一个个节点间传送（快递）
3. 分组交换
   • 数据报
     每个分组被独立处理，每个节点根据一个路由选择算法，每个分组悬着一条路径，使他们的目的地相同（IP）
   • 虚电路
     在数据传输之前，先建立一条逻辑上的连接，每个分组又沿着一条路经传输（X.25、FR、ATM、VPN）
   • 特点：减小网络延迟，提高吞吐量、分组纠错、重发错误分组，通信效率提高。

2.8 多路复用

多路复用技术是把多个低速的信道组合成一个告诉的信道的技术

光纤入户：上网、电视、电话

两个设备：多路复用器、多路分配器

MUX

2.8.1 频分多路复用

无线广播、ADSL、FDD-LTE

2.8.2 时分多路复用

T1/E1、SONET/SDH、WIFI、TDD-LTE

2.8.3 波分多路复用

光纤信号传输

2.8.4 数字传输系统

$T_1$载波也叫一次群，它把24 路话音信道按时分多路的原理复合在一条1.544Mbps 的高速信道上。

$T_1=56K\ast 24+开销与间隔=1.544M$

ITU-T 的E1 信道的数据速率是2.048Mbps (如图2-24 所示）。这种载波把32 个8 位一组的数据样本组合成125μs 的基本帧，其中30 个子信道用千话音传送数据，两个子信道( CH0和CH16) 用于传送控制信，每4 帧能提供64 个控制位。除了北美和亚洲的日本外， E1载波在其他地区得到了广泛使用。

$E_1$每语音64K（=8*8000）

2.8.5 同步数字系列

美国标准叫作同步光纤网络(Synchronous OpticalNetwork, SONET);

ITU-T 以SONET 为基础制订出的国际标准叫作同步数字系列(SynchronousDigital Hierarchy, SDH)

SDH 的基本速率是155.52Mbps

基本速率OC-1约等于50 其他的乘以数字即可。

2.9 差错控制

差错控制原理：传输k位。加入r位冗余（某种算法定义），接收方收到进行计算比较，

接收方知道又差错发生，但不知道是怎样的差错，向发送方请求重传，检错。

接收方知道有差错发生，而且知道是怎样的插叙哦，这种重测策略要纠错。

2.9.1 检错码

奇偶校验：最常见的检错方法，能检出一位错误

原理： 在7位的ASCII码增加一位，使码字中1的个数成奇数或偶数

奇校验：使1的个数为技术

偶校验：使1的个数为偶数

2.9.2 海明码

海明码

海明距离：一个码字要变成另一个码字是必须改变的最小位数

海明码原理：在数据中间加入几个校验码，码距均匀拉大，当某一位出错，会引起几个校验位的值发生变化如果对于m 位的数据增加k 位冗余位，则组成$n=m+k $位的纠错码。对千2m个有效码字中的每一个，都有n个无效但可以纠错的码字。这些可纠错的码字与有效码字的距离是1,含单个错误位。这样，对于一个有效的消息总共有$n+1$个可识别的码字。这n+1个码字相对于其他$2^m-1 $个有效消息的距离都大于1 。这意味着总共有$2^m(n+1）$个有效的或者可纠错的码字。显然，$2^m(n+1)\le 2^n$
这个数应小于等于码字的所有可能的个数，即是，有
海明不等式：m表示消息 n表示校验码的位数
发送消息的长度为k
$k=m+n$

$2^r-1\ge m+r$ 1表示正确的情况

数据位M 校验码P位
k=m+P，

海明吗编码方法

数据 1010

根据海明不等式 $2^n\ge m+n+1$

$m=4得n\ge 3$

海明编码排列

2的n次方位置放置校验码，其他位置数数据位。

(n=0、1、2、3…)

1	2	3	4	5	6	7
$p_1$	$p_2$	1	$p_3$	0	1	0

分组
分组规则

$p_1$和数据位序号二进制第1位的数据位一组

$p_2$和数据位序号二进制第2位的数据位一组

$p_3$和数据位序号二进制第3位的数据位一组

$$\begin{gathered} 1 \\ (001) \end{gathered}$$	$$\begin{gathered} 2 \\ (010) \end{gathered}$$	$$\begin{gathered} 3 \\ (011) \end{gathered}$$	$$\begin{gathered} 4 \\ (100) \end{gathered}$$	$$\begin{gathered} 5 \\ (101) \end{gathered}$$	$$\begin{gathered} 6 \\ (101) \end{gathered}$$	$$\begin{gathered} 7 \\ (111) \end{gathered}$$
$p_1$	$p_2$	1	$p_3$	0	1	0

$$\begin{array}{cccc}{p}_1& m_3& m_5& m_7\\ p_2& m_3& m_6& m_7\\ p_3& m_5& m_6& m_7\end{array}$$

填入数据：

$$\begin{array}{cccc}{p}_1& 1& 0& 0\\ p_2& 1& 1& 0\\ p_3& 0& 1& 0\end{array}$$

通过奇偶校验规则计算校验码的值

奇校验
$$\begin{array}{cccc}{p}_1=0& 1& 0& 0\\ p_2=1& 1& 1& 0\\ p_3=0& 0& 1& 0\end{array}$$

偶校验
$$\begin{array}{cccc}{p}_1=1& 1& 0& 0\\ p_2=0& 1& 1& 0\\ p_3=1& 0& 1& 0\end{array}$$

按照数位填入校验码得到海明码字

奇校验码字

$$\begin{array}{ccccccccc}& 0& 1& 1& 0& 0& 1& 0& \end{array}$$

偶校验码字

$$\begin{array}{ccccccccc}& 1& 0& 1& 1& 0& 1& 0& \end{array}$$

数据传输后进行校验和纠错

1、接收方收到的奇校验海明码数据为
$$\begin{array}{ccccccccc}& 0& 1& 1& 0& 1& 1& 0& \end{array}$$
校验过程：

计算e值，通过e值知道出错的数据位数。
$$\begin{array}{ccccc}{e}_1& p_1& m_3& m_5& m_7\\ e_2& p_2& m_3& m_6& m_7\\ e_3& p_3& m_5& m_6& m_7\end{array}$$
填入数据
$$\begin{array}{ccccc}{e}_1& 0& 1& 1& 0\\ e_2& 1& 1& 1& 0\\ e_3& 0& 1& 1& 0\end{array}$$
通过奇校验规则得到e值。
$$\begin{array}{ccccc}{e}_1=1& 0& 1& 0& 0\\ e_2=0& 1& 1& 1& 0\\ e_3=1& 0& 0& 1& 0\end{array}$$

同过e值算出出错位，
$$\begin{array}{ccc}{e}_3& e_2& e_1\\ 1& 0& 1\end{array}$$
二进制 101=5

所以接收方第5位数据出错，将第五位纠正即可得到正确的数据。
$$\begin{array}{ccccccccc}& 0& 1& 1& 0& 1& 1& 0& \\ & 1& 2& 3& 4& 5& 6& 7& \end{array}$$
更改后得到正确数据
$$\begin{array}{ccccccccc}& 0& 1& 1& 0& 0& 1& 0& \\ & 1& 2& 3& 4& 5& 6& 7& \end{array}$$

2、接受方收到的偶校验海明码数据为
$$\begin{array}{ccccccccc}& 1& 0& 1& 1& 0& 1& 1& \end{array}$$
校验过程：

计算e值，通过e值知道出错的数据位数。
$$\begin{array}{ccccc}{e}_1& p_1& m_3& m_5& m_7\\ e_2& p_2& m_3& m_6& m_7\\ e_3& p_3& m_5& m_6& m_7\end{array}$$
填入数据
$$\begin{array}{ccccc}{e}_1& 1& 1& 0& 1\\ e_2& 0& 1& 1& 1\\ e_3& 1& 0& 1& 1\end{array}$$
通过偶校验规则得到e值。
$$\begin{array}{ccccc}{e}_1=1& 1& 1& 0& 1\\ e_2=1& 0& 1& 1& 1\\ e_3=1& 1& 0& 1& 1\end{array}$$

同过e值算出出错位，
$$\begin{array}{ccc}{e}_3& e_2& e_1\\ 1& 1& 1\end{array}$$
二进制 111=7

所以接收方第7位数据出错，将第七位纠正即可得到正确的数据。
$$\begin{array}{ccccccccc}& 1& 0& 1& 1& 0& 1& 1& \\ & 1& 2& 3& 4& 5& 6& 7& \end{array}$$
更改后得到正确数据
$$\begin{array}{ccccccccc}& 1& 0& 1& 1& 0& 1& 0& \\ & 1& 2& 3& 4& 5& 6& 7& \end{array}$$

3、接收方接收到奇校验数据为
$$\begin{array}{ccccccccc}& 0& 1& 1& 0& 0& 1& 0& \end{array}$$
计算e值
$$\begin{array}{ccccc}{e}_1=0& 0& 1& 0& 0\\ e_2=0& 1& 1& 1& 0\\ e_3=0& 0& 0& 1& 0\end{array}$$

$$\begin{array}{ccc}{e}_3& e_2& e_1\\ 0& 0& 0\end{array}$$
二进制（000）等于0

表示数据传输正确。

2.9.3 循环冗余校验码

CRC循环冗余校验吗能检错不能纠错，

生成多项式：C（x）=X4+

1、校验位的位数，生成多项式的最高次方是几校验位就是几位，

2、补气数据为后面的0 10111 0000

3、提取申城多项式的系数 10011

4、用第二步的结果除以第三位的结果（异或运算）余数不够，补零，余数就是CRC校验码

软考-中级-网络工程师-笔记-第1章-计算机网络概论
软考-中级-网络工程师-笔记-第2章-数据通信基础
软考-中级-网络工程师-笔记-第3章-广域通信网
软考-中级-网络工程师-笔记-第4章-局域网与城域网
软考-中级-网络工程师-笔记-第5章-无线通信
软考-中级-网络工程师-笔记-第6章-网络互联与互联网
软考-中级-网络工程师-笔记-第7章-下一代互联网IPv6
软考-中级-网络工程师-笔记-第8章-网络安全
软考-中级-网络工程师-笔记-第9章 网络操作系统和服务器
软考-中级-网络工程师-笔记-第10章-组网技术
软考-中级-网络工程师-笔记-第11章-网络管理
软考-中级-网络工程师-笔记-第12章-网络规划设计