2023.4.8
归并排序的递归实现
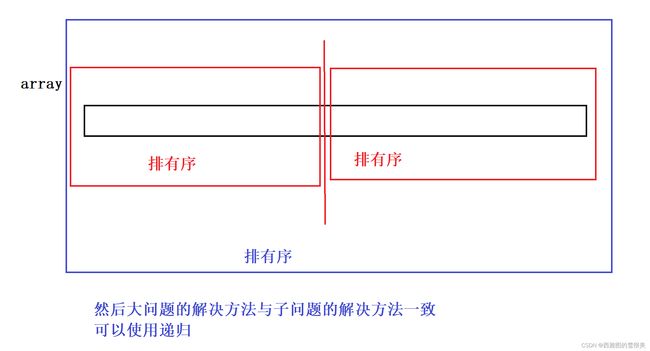
归并排序的递归实现(步骤详解):
实现的逻辑就是:
public static void mergeSort1(int[] array) {
if(array == null || array.length < 2) {
return;
}
// 这个条件必须写上,如果数组是空数组,那么array.length-1就是负数,导致递归进入死循环
sort(array , 0 , array.length-1);
}
public static void sort(int[] array , int L , int R) {
if(L == R) {
return;
}
int mid = L + (R - L) / 2;
sort(array , L , mid); // 注意:范围是【L,mid】而不是【L,mid-1】
sort(array , mid+1 , R);
merge(array , L , mid , R);
// merge函数 : 将两个有序的数组合成一个有序的数组
// 将两个数组的的范围要传过去
}
public static void merge(int[] arr , int L , int mid , int R) {
int[] help = new int[R - L + 1];
// 先创建一个临时数组
int i = 0;
// 一个指针,指向临时数组待放元素的位置
int left = L;
int right = mid + 1;
// 两个指针left 与 right 分别指向两个有序数组的头节点
while(left <= L && right <= R) {
if(arr[left] > arr[right]) {
help[i] = arr[right];
i++;
right++;
}else {
help[i] = arr[left];
i++;
left++;
}
}
while(left <= mid) {
help[i] = arr[left];
left++;
i++;
}
while(right <= R) {
help[i] = arr[right];
right++;
i++;
}
for (int j = 0; j < help.length; j++) {
arr[L + i] = help[j];
}
}
/**
* 分析一下时间复杂度:
* 大问题被均分成了2个小问题,而且每个小问题的规模是一样的,所以对于递归时间复杂度分析可以使用 master公式
* T(N) = 2 * T( N / 2 ) + O(N)
* a = 2 , b = 2 , d = 1
* logb的a = log 2 的 2 == 1 ,d == 1 所以 logb的a==b 所以时间复杂度是:N^b * logN == n*logN
*/
归并排序的非递归实现(步骤详解)
// 归并排序的非递归实现
public class MergeSort {
public static void mergeSort2(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr);
}
public static void process(int[] arr) {
int N = arr.length;
// 步长
int mergeSize = 1;
while (mergeSize < N) {
int L = 0;
while (L < N) {
// 越界条件的判断
if (mergeSize >= N - L) {
break;
}
// L + mergeSize也有可能越界,所以有了上面的代码
int mid = L + mergeSize - 1;
/*
根据越界条件的判断,mid小于N
if (mid > N) {
break;
}
*/
// 有左半部分
int R = Math.min((mid + mergeSize), (N - 1));
merge(arr, L, mid, R);
L = R + 1;
}
// 防止数字越界溢出,导致死循环。
if (mergeSize > (N / 2)) {
break;
}
mergeSize *= 2;
}
}
public static void merge(int[] arr, int L, int mid, int R) {
int[] help = new int[R - L + 1];
int p1 = L;
int p2 = mid + 1;
int i = 0;
while (p1 <= mid && p2 <= R) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
// 后面两个循环只会执行一个,因为P1,P2并不是同时走的
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[L + j] = help[j];
}
}
}
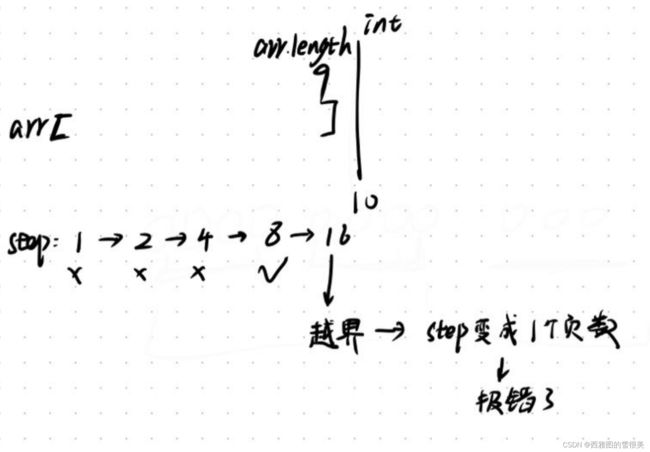
防溢出设计:
当数组的长度非常大时,step*2可能会越界,比如超出整数范围,这样step就会变成负数,这样的话程序就出现错误
当数组长度 N 是偶数时:当step = (N/2) 时就已经可以,此时step < N
当数组长度 N 是奇数时:当step = (N/2)*2 时才可以,此时step < N
即 step小于N就已经排好序了
if (step > N / 2) { // 这个地方不可以写成 (step * 2 > N,这样写铁定step * 2越界)
break;
}
注意边界条件,等号可不可以加,当step是偶数时,step == N / 2 时,就刚好有序
当step是奇数时,step == N / 2还没有序,只有当step = ( N / 2) * 2 时才有序,所以先不可以break,然后进行
step = step * 2这时在进行一系列操作之后就刚好有序,这时再进行溢出判断,step > N / 2, 这样就可以停下了。
数组小和问题:
总结一句话:
传统的比较:是一个一个的进行比较,比较的次数多
归并排序的比较:是一片一片的比较,其中的片是不断的变化的。
一片里面数的变化:1-》 2-》4-》8
public class demo3 {
/**
* 在一个数组中,一个数左边比它小的数的总和,叫该数的小和
* 所有数的小和累加起来,叫数组小和
* 例子: [1,3,4,2,5]
* 1左边比1小的数:没有
* 3左边比3小的数:1
* 4左边比4小的数:1、3
* 2左边比2小的数:1
* 5左边比5小的数:1、3、4、 2
* 所以数组的小和为1+1+3+1+1+3+4+2=16
* 给定一个数组arr,求数组小和
*/
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr, 0, arr.length - 1);
}
// 将arr[L , R] 排有序, 并返回这一范围上的数组小和的值
public static int process(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
int mid = L + ((R - L) >> 1);
return
process(arr, L, mid)
+
process(arr, mid + 1, R)
+
merge(arr, L, mid, R);
}
public static int merge(int[] arr, int L, int mid, int R) {
int[] help = new int[R - L + 1];
int p1 = L;
int p2 = mid + 1;
int i = 0;
int sum = 0;
while (p1 <= mid && p2 <= R) {
/*
if (arr[p1] < arr[p2]) {
sum += arr[p1] * (R - p2 + 1);
help[i++] = arr[p1++];
} else if (arr[p1] == arr[p2]) {
help[i++] = arr[p2++];
} else {
help[i++] = arr[p2++];
}
*/
sum += arr[p1] < arr[p2] ? arr[p1] * (R - p2 + 1) : 0;
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while(p1 <= mid) {
help[i++] = arr[p1++];
}
while(p2 <= R) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[L + j] = help[j];
}
return sum;
}
--------------------------------------------------------------------------------------
// for test
public static int comparator(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int res = 0;
for (int i = 1; i < arr.length; i++) {
for (int j = 0; j < i; j++) {
res += arr[j] < arr[i] ? arr[j] : 0;
}
}
return res;
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// for test
public static int[] copyArray(int[] arr) {
if (arr == null) {
return null;
}
int[] res = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
res[i] = arr[i];
}
return res;
}
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] != arr2[i]) {
return false;
}
}
return true;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// for test
public static void main(String[] args) {
int testTime = 50000;
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);
int[] arr2 = copyArray(arr1);
if (smallSum(arr1) != comparator(arr2)) {
succeed = false;
printArray(arr1);
printArray(arr2);
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}
}
数组逆序
public class ReversePair {
public static int reverPairNumber(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr, 0, arr.length - 1);
}
// 在arr[L , R]上排好序,并返回逆序对数量
public static int process(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
int mid = L + ((R - L) >> 1);
return
process(arr, L, mid)
+
process(arr, mid + 1, R)
+
merge(arr, L, mid, R);
}
public static int merge(int[] arr, int L, int mid, int R) {
int[] help = new int[R - L + 1];
int p1 = L;
int p2 = mid + 1;
int i = 0;
int count = 0;
while (p1 <= mid && p2 <= R) {
// 倒序排列
count += arr[p2] < arr[p1] ? (R - p2 + 1) : 0;
help[i++] = arr[p2] < arr[p1] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[j + L] = help[j];
}
return count;
}
}
翻转对
public class BiggerThanRightTwice {
public int reversePairs(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr, 0, arr.length - 1);
}
// arr[L , R]范围排有序,并且返回该范围上的反转对个数
public static int process(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
int mid = L + ((R - L) >> 1);
return
process(arr, L, mid)
+
process(arr, mid + 1, R)
+
merge(arr, L, mid, R);
}
public static int merge(int[] arr, int L, int mid, int R) {
int p1 = L;
int p2 = mid + 1;
// windowsR: [ , )
int windowsR = mid + 1;
int count = 0;
//------------------------- 先计算
while(p1 <= mid) {
// 小心越界
while(windowsR <= R && ((long)arr[windowsR] * 2) < (long)arr[p1]) {
windowsR++;
}
count += (windowsR - mid - 1);
p1++;
}
//------------------------- 后排序
int[] help = new int[R - L + 1];
int i = 0;
p1 = L;
while (p1 <= mid && p2 <= R) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (int j = 0; j < help.length; j++) {
arr[L + j] = help[j];
}
return count;
}
}