Personalized Federated Learning with Moreau Envelopes论文阅读+代码解析
(好久没更新文章啦,现在开学继续肝)
论文地址点这里
一. 介绍
尽管FL具有数据隐私和减少通信的优势,但它面临着影响其性能和收敛速度的主要挑战:统计多样性,这意味着客户之间的数据分布是不同的(即非i.i.d.)。因此,使用这些非i.i.d.数据训练的全局模型很难在每个客户的数据上得到很好的推广。因此,个性化联邦学习在改变传统追求全局一个较好模型做到了平衡——全局与局部的调整,以适应本地数据集。
二. 相关工作
个性化联邦学习有:混合模型,情景化,元学习和多任务学习。(论文介绍了很多相关论文,在这里不加以赘述)
三. pFedMe
3.1 问题构想
在传统的联邦学习中,在N个客户端时需要解决以下问题:
min w ∈ R d { f ( w ) : = 1 N ∑ i = 1 N f i ( w ) } (1) \min_{w\in\mathbb{R}^d}\{f(w):=\frac{1}{N}\sum^N_{i=1}f_i(w)\} \tag{1} w∈Rdmin{f(w):=N1i=1∑Nfi(w)}(1)
也就是找到一个全局的模型w,其中 f i : R d → R , i = 1 , . . . , N f_i:\mathbb{R}^d\rightarrow\mathbb{R},i=1,...,N fi:Rd→R,i=1,...,N,表示客户端i的损失函数:
f i ( w ) = E ξ i [ f ~ i ( w ; ξ i ) ] f_i(w)=\mathbb{E}_{\xi_i}[\tilde{f}_i(w;\xi_i)] fi(w)=Eξi[f~i(w;ξi)]
其中 ξ i \xi_i ξi表示从客户端i上随意选取一个样本。
在pFedMe中,对损失函数添加一个 l 2 l_2 l2正则项:
f i ( θ i ) + λ 2 ∥ θ i − w ∥ 2 (2) f_i(\theta_i)+\frac{\lambda}{2}\parallel\theta_i-w \parallel^2 \tag{2} fi(θi)+2λ∥θi−w∥2(2)
其中 θ i \theta_i θi表示为客户端i的个性化模型, λ \lambda λ作为超参数控制个性化程度。 λ \lambda λ越大个性化程序越低。基于此,个性化联邦学习被定义为下面的问题:
pFedMe : min w ∈ R d F ( w ) : = 1 N ∑ i = 1 N F i ( w ) , 其中 F i ( w ) = min θ i ∈ R d { f i ( θ i ) + λ 2 ∥ θ i − w ∥ 2 } \text{pFedMe}:\min_{w\in\mathbb{R}^d}{F(w):=\frac{1}{N}\sum^N_{i=1}F_i(w)},\text{其中}F_i(w)=\min_{\theta_i\in\mathbb{R}^d}\{f_i(\theta_i)+\frac{\lambda}{2}\parallel\theta_i-w \parallel^2\} pFedMe:w∈RdminF(w):=N1i=1∑NFi(w),其中Fi(w)=θi∈Rdmin{fi(θi)+2λ∥θi−w∥2}
在pFedMe中,w为各个客户端参数的聚合(外循环), θ i \theta_i θi通过本地数据以及与w的距离进行更新(内循环)。最优个性化模型是pFedME的唯一解决方案,也被称为近端算子,定义如下:
θ i ^ ( w ) : = p r o x f i / λ ( w ) = arg min θ i ∈ R d { f i ( θ i ) + λ 2 ∥ θ i − w ∥ 2 + μ 2 θ i 2 } (3) \hat{\theta_i}(w):=prox_{f_i/\lambda}(w)=\argmin_{\theta_i\in\mathbb{R}^d}\{f_i(\theta_i)+\frac{\lambda}{2}\parallel\theta_i-w \parallel^2+\frac{\mu}2\theta_i^2\}\tag3 θi^(w):=proxfi/λ(w)=θi∈Rdargmin{fi(θi)+2λ∥θi−w∥2+2μθi2}(3)
(根据代码这里我添加了 μ 2 θ i 2 \frac{\mu}2\theta_i^2 2μθi2,作者这里没写出来)
为了比较,作者将Per-FedAvg算法也进行了定义:
min w ∈ R d F ( w ) : = 1 N ∑ i = 1 N F i ( w ) , 其中 θ i ( w ) = w − α ∇ f i ( w ) (4) \min_{w\in\mathbb{R}^d}{F(w):=\frac{1}{N}\sum^N_{i=1}F_i(w)},\text{其中}\theta_i(w)=w-\alpha\nabla f_i(w)\tag4 w∈RdminF(w):=N1i=1∑NFi(w),其中θi(w)=w−α∇fi(w)(4)
Per-Fedavg算法我们之前也提过,其借鉴MAML思想,让客户端获取初始化参数w,再通过w更新 θ i \theta_i θi(详细的可以看我的主页)。
作者表明,本方法和元学习类似,但不同于MAML找到好的初始化参数,pFedMe听过解决一个双层问题追求个性化和全局模型。其有几个优势。一是Ped-FedAvg针对个性化优化了梯度更新,但pFedMe对内部优化器是不可知的,也就是可以多次更新(3)。二是该方法直接优化了 f f f。三是Per-Fedavg需要计算Hessian矩阵而pFedMe只需要使用一阶方法进行梯度计算。
3.2 算法
与联邦学习类似,客户端训练后将参数传给服务器,作者这里用了一个超参数 β \beta β表示对聚合前服务器参数的利用程度,当 β = 1 \beta=1 β=1则为普通的联邦平均。
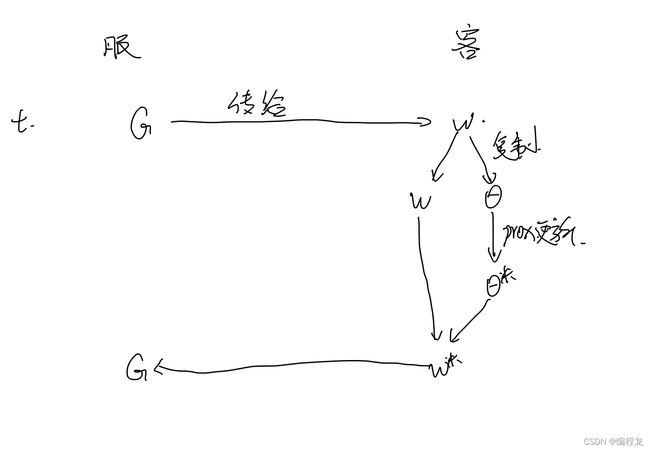
训练时,我们利用式(3)更新我们的参数 θ \theta θ(更新K轮),之后去找 δ \delta δ-approximate去更新w,再将w传入服务端即可。(这里文字叙述有点复杂,建议直接看图)

不懂得小伙伴可以看我之后对应的代码讲解。
四. 代码详解
作者的代码点这里
为了讲解整个过程,我们从t-1轮客户端训练完传给服务器参数开始讲到第t轮。
t-1轮服务器获得一部分客户端的参数,利用 β \beta β参数进行聚合:
def persionalized_aggregate_parameters(self):
assert (self.users is not None and len(self.users) > 0)
# store previous parameters
previous_param = copy.deepcopy(list(self.model.parameters()))
for param in self.model.parameters():
param.data = torch.zeros_like(param.data)
total_train = 0
#if(self.num_users = self.to)
for user in self.selected_users:
total_train += user.train_samples
for user in self.selected_users:
self.add_parameters(user, user.train_samples / total_train)
#self.add_parameters(user, 1 / len(self.selected_users))
# aaggregate avergage model with previous model using parameter beta
for pre_param, param in zip(previous_param, self.model.parameters()):
param.data = (1 - self.beta)*pre_param.data + self.beta*param.data
这里有一个函数self.add_parameters,其为聚合客户端的参数,具体如下:
def add_parameters(self, user, ratio):
model = self.model.parameters()
for server_param, user_param in zip(self.model.parameters(), user.get_parameters()):
server_param.data = server_param.data + user_param.data.clone() * ratio
这里写个公式给大家 G t − 1 G^{t-1} Gt−1表示t-1轮服务器的参数, C i C_i Ci表示客户端的参数,当有l个客户端参与聚合时,如下:
G t = ( 1 − β ) G t − 1 + β J ( C 1 , . . . , C l ) G^t=(1-\beta)G^{t-1}+\beta J(C_1,...,C_l) Gt=(1−β)Gt−1+βJ(C1,...,Cl)
J ( C 1 , . . . , C l ) = G t − 1 + ∑ i = 1 l { 1 l C i } J(C_1,...,C_l)=G^{t-1}+\sum_{i=1}^l\{\frac{1}{l}C_i\} J(C1,...,Cl)=Gt−1+i=1∑l{l1Ci}
之后将聚合好的参数传给客户端,开始客户端训练:
def train(self, epochs):
LOSS = 0
self.model.train()
for epoch in range(1, self.local_epochs + 1): # local update
self.model.train()
X, y = self.get_next_train_batch()
# K = 30 # K is number of personalized steps
for i in range(self.K):
self.optimizer.zero_grad()
output = self.model(X)
loss = self.loss(output, y)
loss.backward()
self.persionalized_model_bar, _ = self.optimizer.step(self.local_model)
# update local weight after finding aproximate theta
for new_param, localweight in zip(self.persionalized_model_bar, self.local_model):
localweight.data = localweight.data - self.lamda* self.learning_rate * (localweight.data - new_param.data)
#update local model as local_weight_upated
#self.clone_model_paramenter(self.local_weight_updated, self.local_model)
self.update_parameters(self.local_model)
return LOSS
其中self.model.weight对应的是 θ \theta θ,self.local_model对应的是 w w w
先更新 θ \theta θ,更新的方法为式(3),对应的代码如下:
def step(self, local_weight_updated, closure=None):
loss = None
if closure is not None:
loss = closure
weight_update = local_weight_updated.copy()
for group in self.param_groups:
for p, localweight in zip( group['params'], weight_update):
p.data = p.data - group['lr'] * (p.grad.data + group['lamda'] * (p.data - localweight.data) + group['mu']*p.data)
return group['params'], loss