Randomized Response论文笔记
1.论文背景
1.1 主要思想:
利用对敏感问题回答的不确定性对原始数据进行隐私保护.
(用撒谎来掩饰)
1.2 核心问题:
在回答隐私问题时,很多人不愿意回答或者是随机回答,因此统计结果的误差通常很难估计.
1.3 解决方案:
Randomized Response ( 随机响应技术)
步骤:1、扰动性统计
2、结果校正
2.主要技术
2.1 技术背景
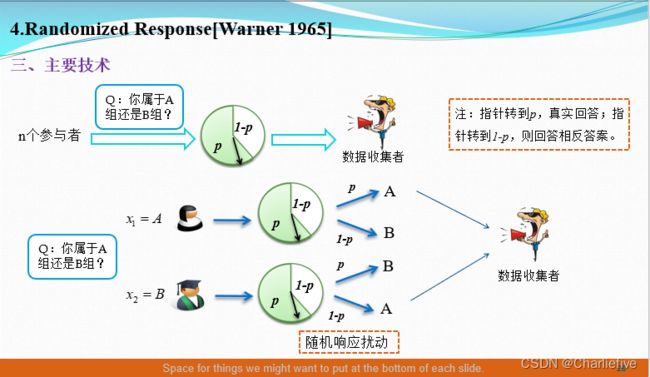
P [ y = A ] = π p + ( 1 − π ) ( 1 − p ) P [ y = B ] = π ( 1 − p ) + ( 1 − π ) p \begin{array}{l} P[{\rm{y}} = A] = \pi p + (1 - \pi )(1 - p)\\ P[y = B] = \pi (1 - p) + (1 - \pi )p \end{array} P[y=A]=πp+(1−π)(1−p)P[y=B]=π(1−p)+(1−π)p
2.2 极大似然函数
极大似然函数:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。极大似然估计原理
因为从收集者的角度Π是未知的,需要构建统计量,构建极大似然函数反推。
L = [ π p + ( 1 − π ) ( 1 − p ) ] n 1 [ π ( 1 − p ) + ( 1 − π ) p ] n − n 1 L = {[\pi p + (1 - \pi )(1 - p)]^{{n_1}}}{[\pi (1 - p) + (1 - \pi )p]^{n - {n_1}}} L=[πp+(1−π)(1−p)]n1[π(1−p)+(1−π)p]n−n1
ln L = n 1 l n [ π p + ( 1 − π ) ( 1 − p ) ] + ( n − n 1 ) l n [ π ( 1 − p ) + ( 1 − π ) p ] \ln L = {n_1}ln[\pi p + (1 - \pi )(1 - p)] + (n - {n_1})ln[\pi (1 - p) + (1 - \pi )p] lnL=n1ln[πp+(1−π)(1−p)]+(n−n1)ln[π(1−p)+(1−π)p]
∂ l n L ∂ π = n 1 ( 2 p − 1 ) π p + ( 1 − π ) ( 1 − p ) + ( n − n 1 ) ( 1 − 2 p ) π ( 1 − p ) + ( 1 − π ) p = 0 \frac{{\partial lnL}}{{\partial \pi }} = \frac{{{n_1}(2p - 1)}}{{\pi p + (1 - \pi )(1 - p)}} + \frac{{(n - {n_1})(1 - 2p)}}{{\pi (1 - p) + (1 - \pi )p}} = 0 ∂π∂lnL=πp+(1−π)(1−p)n1(2p−1)+π(1−p)+(1−π)p(n−n1)(1−2p)=0
通过极大似然估计得到属于A组占比的估计量:
π ^ = p − 1 2 p − 1 + n 1 ( 2 p − 1 ) n \hat \pi = \frac{{p - 1}}{{2p - 1}} + \frac{{{n_1}}}{{(2p - 1)n}} π^=2p−1p−1+(2p−1)nn1
希望它是无偏的,即与真实值越接近越好:
E ( π ^ ) = E ( p − 1 2 p − 1 + n 1 ( 2 p − 1 ) n ) = 1 2 p − 1 ( p − 1 + π p + ( 1 − π ) ( 1 − p ) ) = π E(\hat \pi ) = E\left( {\frac{{p - 1}}{{2p - 1}} + \frac{{{n_1}}}{{(2p - 1)n}}} \right) = \frac{1}{{2p - 1}}\left( {p - 1 + \pi p + (1 - \pi )(1 - p)} \right) = \pi E(π^)=E(2p−1p−1+(2p−1)nn1)=2p−11(p−1+πp+(1−π)(1−p))=π
由此可得到校正的统计值,用N表示统计得到的属于A组人数的估计值:
N = π ^ n = p − 1 2 p − 1 n + n 1 2 p − 1 N = \hat \pi n = \frac{{p - 1}}{{2p - 1}}n + \frac{{{n_1}}}{{2p - 1}} N=π^n=2p−1p−1n+2p−1n1
2.3 方差
V a r ( π ^ ) = V a r ( p − 1 2 p − 1 + n 1 ( 2 p − 1 ) n ) = 1 ( 2 p − 1 ) 2 n V a r ( n 1 n ) Var(\hat \pi ) = Var(\frac{{p - 1}}{{2p - 1}} + \frac{{{n_1}}}{{(2p - 1)n}}) = \frac{1}{{{{(2p - 1)}^2}n}}Var(\frac{{{n_1}}}{n}) Var(π^)=Var(2p−1p−1+(2p−1)nn1)=(2p−1)2n1Var(nn1)

E ( x i ) = π p + ( 1 − π ) ( 1 − p ) E({x_i}) = \pi p + (1 - \pi )(1 - p) E(xi)=πp+(1−π)(1−p)
E ( x i 2 ) = π p + ( 1 − π ) ( 1 − p ) E(x_i^2) = \pi p + (1 - \pi )(1 - p) E(xi2)=πp+(1−π)(1−p)
直接根据方差的定义开始算:
D ( x i ) = E ( x i 2 ) − E 2 ( x i ) = π p + ( 1 − π ) ( 1 − p ) − [ π p + ( 1 − π ) ( 1 − p ) ] 2 D({x_i}) = E(x_i^2) - {E^2}({x_i}) = \pi p + (1 - \pi )(1 - p) - {[\pi p + (1 - \pi )(1 - p)]^2} D(xi)=E(xi2)−E2(xi)=πp+(1−π)(1−p)−[πp+(1−π)(1−p)]2
= − 4 π 2 p 2 + 4 π 2 p + 4 π p 2 − 4 π p − π 2 − p 2 + π + p = - 4{\pi ^2}{p^2} + 4{\pi ^2}p + 4\pi {p^2} - 4\pi p - {\pi ^2} - {p^2} + \pi + p =−4π2p2+4π2p+4πp2−4πp−π2−p2+π+p
V a r ( π ^ ) = − 4 π 2 p 2 + 4 π 2 p + 4 π p 2 − 4 π p − π 2 − p 2 + π + p ( 2 p − 1 ) 2 n Var(\hat \pi ) = \frac{{ - 4{\pi ^2}{p^2} + 4{\pi ^2}p + 4\pi {p^2} - 4\pi p - {\pi ^2} - {p^2} + \pi + p}}{{{{(2p - 1)}^2}n}} Var(π^)=(2p−1)2n−4π2p2+4π2p+4πp2−4πp−π2−p2+π+p
接下来对该公式进行化简:
= 4 π 2 ( p − p 2 ) + 4 π ( p 2 − p ) − ( p 2 − p ) + π − π 2 4 n ( p − 1 / 2 ) 2 = ( p − p 2 ) ( 4 π 2 − 4 π + 1 ) + π − π 2 4 n ( p − 1 / 2 ) 2 = [ 1 4 − ( p − 1 2 ) 2 ] [ 4 ( π − 1 2 ) 2 ] − ( π − 1 2 ) 2 + 1 4 4 n ( p − 1 / 2 ) 2 = 1 4 − 4 ( p − 1 2 ) 2 ( π − 1 2 ) 2 4 n ( p − 1 / 2 ) 2 = 1 n [ 1 16 ( p − 1 / 2 ) 2 − ( π − 1 2 ) 2 ] \begin{array}{l} = \frac{{4{\pi ^2}(p - {p^2}) + 4\pi ({p^2} - p) - ({p^2} - p) + \pi - {\pi ^2}}}{{4n{{(p - 1/2)}^2}}}\\ = \frac{{(p - {p^2})(4{\pi ^2} - 4\pi + 1) + \pi - {\pi ^2}}}{{4n{{(p - 1/2)}^2}}}\\ = \frac{{[\frac{1}{4} - {{(p - \frac{1}{2})}^2}][4{{(\pi - \frac{1}{2})}^2}] - {{(\pi - \frac{1}{2})}^2} + \frac{1}{4}}}{{4n{{(p - 1/2)}^2}}}\\ = \frac{{\frac{1}{4} - 4{{(p - \frac{1}{2})}^2}{{(\pi - \frac{1}{2})}^2}}}{{4n{{(p - 1/2)}^2}}} = \frac{1}{n}[\frac{1}{{16{{(p - 1/2)}^2}}} - {(\pi - \frac{1}{2})^2}] \end{array} =4n(p−1/2)24π2(p−p2)+4π(p2−p)−(p2−p)+π−π2=4n(p−1/2)2(p−p2)(4π2−4π+1)+π−π2=4n(p−1/2)2[41−(p−21)2][4(π−21)2]−(π−21)2+41=4n(p−1/2)241−4(p−21)2(π−21)2=n1[16(p−1/2)21−(π−21)2]
V a r ( π ^ ) = 1 n { [ 1 4 − ( π − 1 2 ) 2 ] + [ 1 16 ( p − 1 / 2 ) 2 − 1 4 ] } Var(\hat \pi ) = \frac{1}{n}\left\{ {\left[ {\frac{1}{4} - {{\left( {\pi - \frac{1}{2}} \right)}^2}} \right] + \left[ {\frac{1}{{16{{\left( {p - 1/2} \right)}^2}}} - \frac{1}{4}} \right]} \right\} Var(π^)=n1{[41−(π−21)2]+[16(p−1/2)21−41]}
最后分解成两部分,分别是采样的误差(左)和随机机制的误差(右)。其中可观察到控制p当p=1/2时候方差无限大,是完全随机的;当p=1时,随即机制产生的误差就消失了。
2.4 偏差和方差
偏差bias:度量了某种学习算法的平均估计结果所能逼近学习目标的程度即 期望预测与真实结果的偏离程度,算法本身的拟合能力模型的精密度)
方差variance:模型的每一次输出结果与模型的输出期望值之间的误差模型的稳定性,数据是否集中)
3.LDP Frequency estimation
- 学会画概率树,了解每次抛硬币概率变化
- 学会从真实概率到数据收集着之间的概率不一样,中间经过几次扰动
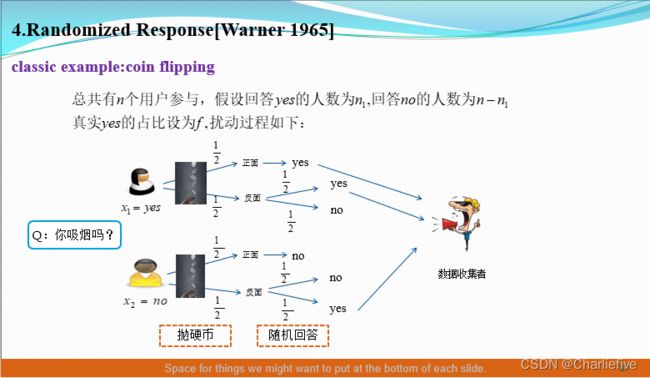
过程:当第一次为正面时候,如是回答;若为反面,抛第二次硬币,若为正面,继续如实回答,若为反面,相反回答。(如实回答就是用户本身的概率,见下面公式)
统计扰动结果:
P [ y = y e s ] = 1 2 P [ x = y e s ] + 1 2 ∗ 1 2 P [ x = y e s ] + 1 2 ∗ 1 2 P [ x = n o ] P [ y = n o ] = 1 2 P [ x = n o ] + 1 2 ∗ 1 2 P [ x = n o ] + 1 2 ∗ 1 2 P [ x = y e s ] \begin{array}{l} P[y = yes] = \frac{1}{2}P[x = yes] + \frac{1}{2}*\frac{1}{2}P[x = yes] + \frac{1}{2}*\frac{1}{2}P[x = no]\\ P[y = no] = \frac{1}{2}P[x = no] + \frac{1}{2}*\frac{1}{2}P[x = no] + \frac{1}{2}*\frac{1}{2}P[x = yes] \end{array} P[y=yes]=21P[x=yes]+21∗21P[x=yes]+21∗21P[x=no]P[y=no]=21P[x=no]+21∗21P[x=no]+21∗21P[x=yes]
P [ y = y e s ] = 1 2 f + 1 4 f + 1 4 ( 1 − f ) P [ y = n o ] = 1 2 ( 1 − f ) + 1 4 ( 1 − f ) + 1 4 f \begin{array}{l} P[y = yes] = \frac{1}{2}f + \frac{1}{4}f + \frac{1}{4}(1 - f)\\ P[y = no] = \frac{1}{2}(1 - f) + \frac{1}{4}(1 - f) + \frac{1}{4}f \end{array} P[y=yes]=21f+41f+41(1−f)P[y=no]=21(1−f)+41(1−f)+41f
相当于3/4的人说真话,1/4的人说假话。
注意这里扰动概率和采样概率的设置:

构建似然函数: L = ( 1 2 f − 1 4 ) n 1 ( 3 4 − 1 2 f ) n − n 1 L = {(\frac{1}{2}f - \frac{1}{4})^{{n_1}}}{(\frac{3}{4} - \frac{1}{2}f)^{n - {n_1}}} L=(21f−41)n1(43−21f)n−n1
取对数: ln L = n 1 ln ( 1 2 f + 1 4 ) + ( n − n 1 ) ln ( 3 4 − 1 2 f ) \ln L = {n_1}\ln (\frac{1}{2}f + \frac{1}{4}) + (n - {n_1})\ln (\frac{3}{4} - \frac{1}{2}f) lnL=n1ln(21f+41)+(n−n1)ln(43−21f)
求导: α ln L α f = 1 2 n 1 1 2 f + 1 4 + − 1 2 ( n − n 1 ) 3 4 − 1 2 f = 0 \frac{{\alpha \ln L}}{{\alpha f}} = \frac{{\frac{1}{2}{n_1}}}{{\frac{1}{2}f + \frac{1}{4}}} + \frac{{ - \frac{1}{2}(n - {n_1})}}{{\frac{3}{4} - \frac{1}{2}f}} = 0 αfαlnL=21f+4121n1+43−21f−21(n−n1)=0
通过极大似然估计得到yes占比的估计量: f ^ = 2 n 1 − 1 2 n n \hat f = \frac{{2{n_1} - \frac{1}{2}n}}{n} f^=n2n1−21n
估计量的无偏性: E ( f ^ ) = E ( 2 n 1 − 1 2 n n ) = 2 P [ y = y e s ] − 1 2 = 2 ( 1 2 f + 1 4 ) − 1 2 = f E(\hat f) = E(\frac{{2{n_1} - \frac{1}{2}n}}{n}) = 2P[y = yes] - \frac{1}{2} = 2(\frac{1}{2}f + \frac{1}{4}) - \frac{1}{2} = f E(f^)=E(n2n1−21n)=2P[y=yes]−21=2(21f+41)−21=f
估计量的方差: V a r ( f ^ ) = V a r ( 2 n 1 − 1 2 n n ) = 4 n 2 V a r ( n 1 ) = 4 n P [ y = y e s ] P [ y = n o ] n 2 = 4 ( 1 2 f + 1 4 ) ( 3 4 − 1 2 f ) n = f ( 1 − f ) n + 3 / 4 n Var(\hat f) = Var(\frac{{2{n_1} - \frac{1}{2}n}}{n}) = \frac{4}{{{n^2}}}Var({n_1}) = \frac{{4nP[y = yes]P[y = no]}}{{{n^2}}}\\ = \frac{{4(\frac{1}{2}f + \frac{1}{4})(\frac{3}{4} - \frac{1}{2}f)}}{n}\\ = \frac{{f(1 - f)}}{n} + \frac{{3/4}}{n} Var(f^)=Var(n2n1−21n)=n24Var(n1)=n24nP[y=yes]P[y=no]=n4(21f+41)(43−21f)=nf(1−f)+n3/4

