Numpy 100 exercise 笔记

Intro

之前一直使用的是anaconda的Jupyter来打python代码，最近想学习PyCharm，因此开始了numpy 100 练习作为numpy包的复习和整理，顺带熟悉一下PyCharm。本文章里会有代码和一些学习笔记，随写随更，文章较长，适合新手观看。

1. Import the numpy package under the name np(★☆☆)

import numpy as np

2. Print the numpy version and the configuration (★☆☆)

打印输出numpy的版本和配置信息

print(np.__version__)
np.show_config()

3. Create a null vector of size 10(★☆☆)

创建长度为10的零向量

Z = np.zeros(10)
print(Z)

如果需要输出一堆零向量，需要使用np里面的zeros函数 （zeros(shape, dtype=float, order=‘C’)）， 这个函数会返回一个相应大小和类型的零矩阵。默认的dtype是numpy.float64。order可以选’C’（行优先）或是’F’（列优先）。本题要求长度为10，如果要的是一个n*m矩阵的话便是 np.zeros((n, m))。举例如下：

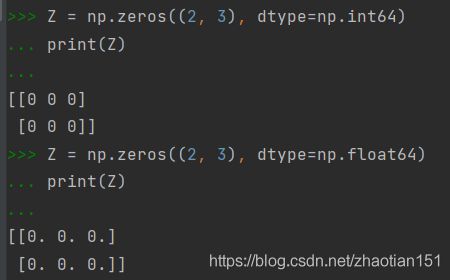
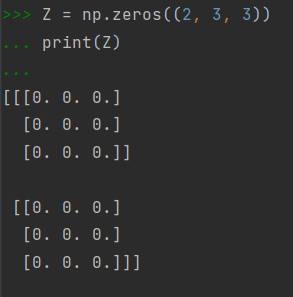
三维的同理，np.zeros((z, n, m))

4. How to find the memory size of any array(★☆☆)

获取数组所占内存大小

Z = np.zeros((10,10))
print("%d bytes" % (Z.size * Z.itemsize))
# or
print((Z.size * Z.itemsize), "bytes")

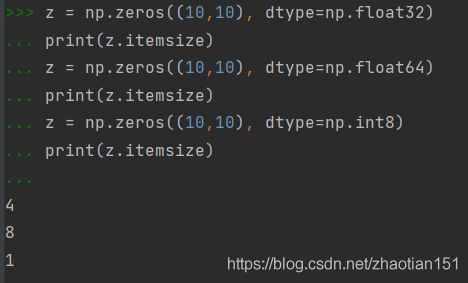
z.size就是10x10 = 100， itemsize是字节单位长度，要注意的是不同的dtype的itemsize是不一样的。

5. How to get the documentation of the numpy add function from the command line? (★☆☆)

怎么用命令行获取numpy add函数的文档说明？

np.info(np.add)

6. Create a null vector of size 10 but the fifth value which is 1 (★☆☆)

创建一个长度为10的零向量，并把第五个值赋值为1

Z = np.zeros(10)
Z[4] = 1
print(Z)

这里要知道python是从0开始计数的，因此第一个值是Z[0], 第二个是Z[1]…第五个是Z[4]

7. Create a vector with values ranging from 10 to 49 (★☆☆)

创建一个值域为10到49的向量

Z = np.arange(10,50)
print(Z)

np.arange()这个函数可以返回一个有终点和起点的固定步长的数列，可以有1，2或是3个参数。分别如下：

8. Reverse a vector (first element becomes last) (★☆☆)

将一个向量进行反转（第一个元素变为最后一个元素）

Z = np.arange(10)
Z = Z[::-1]
print(Z)

Z = np.arange(10)
Z = np.flipud(Z)
print(Z)

两个方法，第一种的意思是把列表从后往前数，最后一位是-1。第二种直接使用flipud函数，这个函数也可以反转矩阵。

9. Create a 3x3 matrix with values ranging from 0 to 8 (★☆☆)

创建一个3x3的矩阵，值域为0到8(★☆☆)

Z = np.arange(9).reshape(3, 3)
print(Z)

首先用arange创建一个0到8的数列，然后用reshape改变形状。reshape跟前面提到的zeros一样，可以做1、2、3维的转换。举例如下：

10. Find indices of non-zero elements from [1,2,0,0,4,0] (★☆☆)

从数组[1, 2, 0, 0, 4, 0]中找出非0元素的位置索引

nz = np.nonzero([1,2,0,0,4,0])
print(nz)

nonzero()函数返回的是数组中，非零元素的位置。也可以应用于二维、三维数组。举例如下：

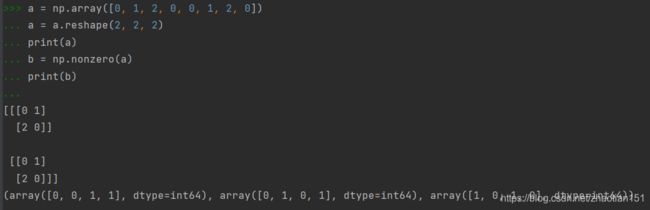
我们建立了一个三维数组，最后输出的 (array([0, 0, 1, 1], dtype=int64), array([0, 1, 0, 1], dtype=int64), array([1, 0, 1, 0], dtype=int64)) 代表了这个三维数组中非零元素的位置，我们看到每个array都有四位，这代表了数组里面有4个非零元素。看每一个array的第一位，分别是0，0，1，代表第一个非零元素在第一组第一行的第二位。看每一个array的第一位，分别是0，1，0，代表第二个非零元素在第一组第二行的第一位。以此类推。

11. Create a 3x3 identity matrix (★☆☆)

创建一个3x3的单位矩阵

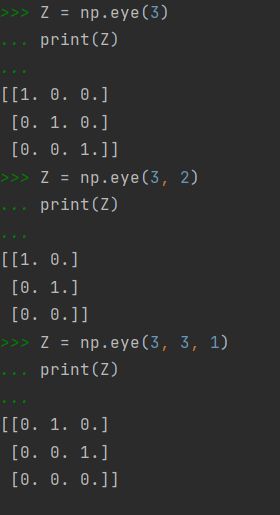
Z = np.eye(3)
print(Z)

首先来了解一下identity matrix 单位矩阵是个啥，这个是在数学中很常用的一种，任何矩阵与其相乘都等于本身，它是个方阵，从左上角到右下角的对角线（主对角线）上的元素均为1。除此以外全都为0。
np.eye()这个方程就是用来创建该矩阵用的。模式为numpy.eye(N, M=None, k=0)，其中N为行数，M为列数（如果不设置的话默认为N），k是对角线的位置。打几行代码来看看他们的区别。

12. Create a 3x3x3 array with random values (★☆☆)

创建一个3x3x3的随机数组

Z = np.random.random((3, 3, 3))
print(Z)

Z = np.random.rand(3, 3, 3)
print(Z)

以上两种都可以，np.random.rand() 函数可以生成指定维度的的[0,1)范围之间的随机数，输入参数为维度。np.random.random(size = ())和上面的一样可以生成[0,1)范围内的随机浮点数阵列。

13. Create a 10x10 array with random values and find the minimum and maximum values (★☆☆)

创建一个10x10的随机数组，并找出该数组中的最大值与最小值。

Z = np.random.random((10, 10))
Zmin, Zmax = Z.min(), Z.max()
print(Zmin, Zmax)

14. Create a random vector of size 30 and find the mean value (★☆☆)

创建一个长度为30的随机向量，并求它的平均值。

创建一个长度为30的随机向量，并求它的平均值 

15. Create a 2d array with 1 on the border and 0 inside (★☆☆)

创建一个2维数组，该数组边界值为1，内部的值为0 。

Z = np.ones((3, 3))
Z[1:-1, 1:-1] = 0
print(Z)

这个np.ones跟np.zeros一样，只不过把0换成了1。首先创建一个全是1的数组，然后把内部填0即可。

16. How to add a border (filled with 0’s) around an existing array? (★☆☆)

如何用0来填充一个数组的边界？

Z = np.ones((5, 5))
Z = np.pad(Z, pad_width=1, mode='constant', constant_values=0)
print(Z)

Z = np.ones((5, 5))
Z[:, [0, -1]] = 0
Z[[0, -1], :] = 0
print(Z)

两种方法，第一种是在数组外面套一个数值为0的圈，第二种是把数组的最外面一圈改成0。
np.pad()可以将numpy数组按指定的方法填充成指定的形状，这个在深度学习中的数据预处理的时候比较常用到。这里面的参数pad_width是填充的宽度，mode是填充的方法，pad里面的填充方法有很多，感兴趣的可以去搜索一下。

17. What is the result of the following expression? (★☆☆)

下面表达式运行的结果是什么？

print(0 * np.nan)             #nan
print(np.nan == np.nan)       #False
print(np.inf > np.nan)        #False
print(np.nan - np.nan)        #nan
print(np.nan in set([np.nan]))#True
print(0.3 == 3 * 0.1)         #False

NaN是Not a Number （非数），表示未定义或不可表示的值。inf是infinity，代表无穷。
0.3 != 30.1是因为python储存中对double型数据有一定的精度误差。这个在python里面算一下就会发现不一样了，30.1 = 0.30000000000000004。

18. Create a 5x5 matrix with values 1,2,3,4 just below the diagonal (★☆☆)

创建一个5x5的矩阵，且设置值1, 2, 3, 4在其对角线下面一行。

Z = np.diag(1+np.arange(4), k=-1)
print(Z)

来看一下diag的官方文档哈，numpy.diag(v, k) 这个函数可以以一维数组的形式返回方阵的对角线（或非对角线）元素，或将一维数组转换成方阵（非对角线元素为0）。如果v是2D数组，返回k位置的对角线。如果v是1D数组，返回一个v作为k位置对角线的2维数组。
那么本题的解法就是先创建一个[1，2，3，4]的1D数组，然后k位置为-1 （对角线的位置向下移一行）。

19. Create a 8x8 matrix and fill it with a checkerboard pattern (★☆☆)

创建一个8x8的国际象棋棋盘矩阵（黑块为0，白块为1）

Z = np.zeros((8, 8), dtype=int)
Z[1::2, 0::2] = 1
Z[0::2, 1::2] = 1
print(Z)

这题先建立一个全都是0的8x8矩阵，然后从第1行开始往下每两行的第0列开始往右每两列为1 （Z[1::2, 0::2] = 1），从第0行开始往下每两行的第1列开始往右每两列为1 （Z[0::2, 1::2] = 1）。或者建立1矩阵然后填0也可~

20. Consider a (6,7,8) shape array, what is the index (x,y,z) of the 100th element? (★☆☆)

思考一下形状为(6, 7, 8)的数组，第100个元素的索引(x, y, z)分别是什么？

print(np.unravel_index(100, (6, 7, 8)))

numpy.unravel_index(indices, dims) 函数的作用是获取一个/多个索引值在一个多维数组中的位置。

21. Create a checkerboard 8x8 matrix using the tile function (★☆☆)

用tile函数创建一个8x8的棋盘矩阵

Z = np.tile(np.array([[0,1],[1,0]]), (4,4))
print(Z)

tile这个词就是拼接，铺瓷砖的意思。在这里就是将原矩阵横向、纵向地复制。这个很好理解，就是建立一个小矩阵，然后把这个矩阵根据根据要求像铺瓷砖一样铺开。

22. Normalize a 5x5 random matrix (★☆☆)

对5x5的随机矩阵进行归一化

Z = np.random.random((5, 5))
Zmax, Zmin = Z.max(), Z.min()
Z = (Z-Zmin)/(Zmax-Zmin)
print (Z)

首先要知道归一化是啥。很多人会把归一化（normalize）和标准化（standardize）弄混。
归一化可以将数据映射到0~1之间，去掉量纲，让计算更加合理，不会因为量纲问题导致1米与100mm产生不同。

标准化则是消除分布产生的度量偏差。

这里再给一个标准化的代码：

Z = np.random.random((5,5))
Z = (Z - np.mean (Z)) / (np.std (Z))
print(Z)

23. Create a custom dtype that describes a color as four unsigned bytes (RGBA) (★☆☆)

创建一个dtype来表示颜色(RGBA)

color = np.dtype([("r", np.ubyte, 1),
                  ("g", np.ubyte, 1),
                  ("b", np.ubyte, 1),
                  ("a", np.ubyte, 1)])
print(color)

24. Multiply a 5x3 matrix by a 3x2 matrix (real matrix product) (★☆☆)

一个5x3的矩阵和一个3x2的矩阵相乘，结果是什么？

Z = np.dot(np.ones((5, 3)), np.ones((3, 2)))
print(Z)

Z = np.ones((5, 3)) @ np.ones((3, 2))
print(Z)

矩阵相乘用点乘（dot）。第二个方法的 @ 应该是python3.5版本以上可以用的。

25. Given a 1D array, negate all elements which are between 3 and 8, in place. (★☆☆)

给定一个一维数组把它索引从3到8的元素求相反数

Z = np.arange(11)
Z[(3 < Z) & (Z < 8)] *= -1
print(Z)

A += 1 和 A=A + 1 是一样的，其他运算同理。

26. What is the output of the following script? (★☆☆)

下面的脚本的结果是什么？

print(sum(range(5), -1))  # 9

from numpy import *
print(sum(range(5), -1))  # 10

这俩的运行结果是不一样的，第二个print里面使用到的是numpy.sum(a, axis=None)。第一个则是python自己的sum函数。

27. Consider an integer vector Z, which of these expressions are legal? (★☆☆)

关于整数向量Z下面哪些表达式正确？

'Z**Z           True'
'2 << Z >> 2    False'
'Z <- Z         True'
'1j*Z           True'
'Z/1/1          True'
'ZZ          False'

28. What are the result of the following expressions? (★☆☆)

下面表达式的结果分别是什么？

print(np.array(0) / np.array(0))                     # nan
print(np.array(0) // np.array(0))                    # 0
print(np.array([np.nan]).astype(int).astype(float))  # -2.14748365e+09

29. How to round away from zero a float array ? (★☆☆)

如何从零位开始舍入浮点数组？

Z = np.random.uniform(-10, +10, 10)
print(np.copysign(np.ceil(np.abs(Z)), Z))

'More readable but less efficient'
print(np.where(Z > 0, np.ceil(Z), np.floor(Z)))

np.ceil(a) 和 np.floor(a) : 是取元素的整值（ceiling向上取整，floor向下取整）。
numpy.copysign(x1, x2）：将x1的符号改为x2的符号，按元素排序。
第一个解法首先对数组Z取了绝对值 np.abs(Z)， 然后对取了绝对值的数组取整，最后把原始数组的正负号copy过来。
第二个解法很好理解，但是效率相对第一个要慢一些。

30.How to find common values between two arrays? (★☆☆)

如何找出两个数组公共的元素?

Z1 = np.random.randint(0, 10, 10)
Z2 = np.random.randint(0, 10, 10)
print(np.intersect1d(Z1, Z2))

可以使用numpy中的intersect1d() 这个函数找出两个array中的交集。

31. How to ignore all numpy warnings (not recommended)? (★☆☆)

如何忽略numpy的警告信息（不推荐）

# Suicide mode on
defaults = np.seterr(all="ignore")
Z = np.ones(1) / 0

# Back to sanity
_ = np.seterr(**defaults)

# Equivalently with a context manager
with np.errstate(all="ignore"):
    np.arange(3) / 0

32. Is the following expressions true? (★☆☆)

下面的表达式是否为真?

np.sqrt(-1) == np.emath.sqrt(-1)  # False

33. How to get the dates of yesterday, today and tomorrow? (★☆☆)

如何获得昨天，今天和明天的日期?

yesterday = np.datetime64('today') - np.timedelta64(1)
today     = np.datetime64('today')
tomorrow  = np.datetime64('today') + np.timedelta64(1)

34. How to get all the dates corresponding to the month of July 2016? (★★☆)

怎么获得所有与2016年7月的所有日期?

Z = np.arange('2016-07', '2016-08', dtype='datetime64[D]')
print(Z)

35. How to compute ((A+B)*(-A/2)) in place (without copy)? (★★☆)

如何计算 ((A+B)*(-A/2)) (不使用中间变量)?

A = np.ones(3)*1
B = np.ones(3)*2
np.add(A, B, out=B)
np.divide(A, 2, out=A)
np.negative(A, out=A)
np.multiply(A, B, out=A)
print(A)

36. Extract the integer part of a random array of positive numbers using 4 different methods (★★☆)

用4种不同的方法提取随机数组中的整数部分。

Z = np.random.uniform(0, 10, 10)

print(Z - Z%1)
print(Z // 1)
print(np.floor(Z))
print(Z.astype(int))
print(np.trunc(Z))

37. Create a 5x5 matrix with row values ranging from 0 to 4 (★★☆)

创建一个5x5的矩阵且每一行的值范围为从0到4

Z = np.zeros((5, 5))
Z += np.arange(5)
print(Z)

' without broadcasting'
Z = np.tile(np.arange(0, 5), (5, 1))
print(Z)

38. Consider a generator function that generates 10 integers and use it to build an array (★☆☆)

如何用一个生成10个整数的函数来构建数组

def generate():
    for x in range(10):
        yield x
Z = np.fromiter(generate(), dtype=float, count=-1)
print(Z)

我们来看一下yield是啥，简单地讲，yield 的作用就是把一个函数变成一个 generator，带有 yield 的函数不再是一个普通函数，Python 解释器会将其视为一个 generator，调用 generate() 不会执行 generate函数，而是返回一个 iterable 对象。在 for 循环执行时，每次循环都会执行 generate函数内部的代码，执行到 yield x 时，generate函数就返回一个迭代值，下次迭代时，代码从 yield x 的下一条语句继续执行，而函数的本地变量看起来和上次中断执行前是完全一样的，于是函数继续执行，直到再次遇到 yield。
numpy.fromiter(iterable, dtype, count = - 1) 这个函数用于通过使用可迭代对象来创建ndarray。它返回一维ndarray对象。

39. Create a vector of size 10 with values ranging from 0 to 1, both excluded (★★☆)

创建一个大小为10的向量， 值域为0到1，不包括0和1

Z = np.linspace(0, 1, 11,endpoint=False)[1:]
print(Z)

linspace函数用于创建一个是等差数列的一维数组。默认的是endpoint = True，这里因为不包括1，所以设置为False。

40. Create a random vector of size 10 and sort it (★★☆)

创建一个长度为10的随机向量并且排序

Z = np.random.random(10)
Z.sort()
print(Z)

41. How to sum a small array faster than np.sum? (★★☆)

如何对一个小的数组进行相加且速度快于np.sum

Z = np.arange(10)
np.add.reduce(Z)

python文档里面说 add.reduce() is equivalent to sum()，代表这俩运算结果和代码书写不会有啥区别。有网友测试，对于相对较小的数组大小，add.reduce大约快两倍。

42. Consider two random array A and B, check if they are equal (★★☆)

检查两个随机数列A和B是否相等。

A = np.random.randint(0, 2, 5)
B = np.random.randint(0, 2, 5)

'Assuming identical shape of the arrays and a tolerance for the comparison of values'
equal = np.allclose(A, B)
print(equal)

'Checking both the shape and the element values, no tolerance (values have to be exactly equal)'
equal = np.array_equal(A, B)
print(equal)

第一个是只要array的形状(shape)相同并且数值大致相同（有一个容差tolerance）即可。第二个是需要全部相等。

43. Make an array immutable (read-only) (★★☆)

把数组变为只读

Z = np.zeros(10)
Z.flags.writeable = False
Z[0] = 1

44. Consider a random 10x2 matrix representing Cartesian coordinates, convert them to polar coordinates (★★☆)

将一个10x2的笛卡尔坐标矩阵转换为极坐标

Z = np.random.random((10, 2))
X,  Y = Z[:, 0], Z[:, 1]
R = np.sqrt(X**2+Y**2)
T = np.arctan2(Y, X)
print(R)
print(T)

首先建立10x2的一个矩阵Z，然后X，Y分别是矩阵的第一列和第二列。

参照公式，计算出R和T即可。

45. Create random vector of size 10 and replace the maximum value by 0 (★★☆)

把一个尺寸为10的随机向量的最大值替换成0.

Z = np.random.random(10)
Z[Z.argmax()] = 0
print(Z)

argmax（）这个函数返回的是最大数的索引，之际把最大值所在的位置上面的数换成0就可以啦。

46. Create a structured array with x and y coordinates covering the [0,1]x[0,1] area (★★☆)

创建一个结构化数组，其中x和y坐标覆盖[0, 1]x[1, 0]区域。

Z = np.zeros((5, 5), [('x', float), ('y', float)])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0, 1, 5),
                             np.linspace(0, 1, 5))
print(Z)

47.

48.

49.

50. How to find the closest value (to a given scalar) in a vector?

如何在数组中找到与给定标量接近的值?

z = np.arange(100)
v = np.random.uniform(0, 100)
index = (np.abs(z - v)).argmin()
print(z[index])

51. Create a structured array representing a position (x,y) and color