Python prep 随想练习 Day7-红黑树

Day7-part1

Balanced Binary Trees, Red-Black Trees 平衡二叉树，红黑树

平衡二叉树

先回忆一下一个概念叫做二叉搜索树，BST。他的特点是：left < middle < right
在Day7的所有讨论中，我们的二叉树都是二叉搜索树。

当我们利用BST在进行搜索时，搜索特定值的方法是什么呢？
应该是 判断 value( < = > )cur.value，如果小于: cur=cur.left ; 如果大于: cur=cur.right；如果等于，return

通过这样的方法完成搜索，比较理想的情况，时间复杂度应该是O（logn），但是如果这颗BST结构不是特别ok呢？比如全部位于一侧的话，那么二叉树其实就类似于一个单链表，时间复杂度退化为O（n），太慢了！

为了避免这样的情况发生，我们应该采取什么措施避免呢？
我们应用了平衡二叉搜索树，balanced BST
平衡二叉搜索树的性质：

1. 包含二叉搜索树的基本性质：left的value值 < middle的value值 < right的value值
2. 对于balanced BST，它的任意子树也还是balanced BST
3. 左右子节点的高度差最多为1 （下面第一个图是balanced 第二个图是unbalanced）

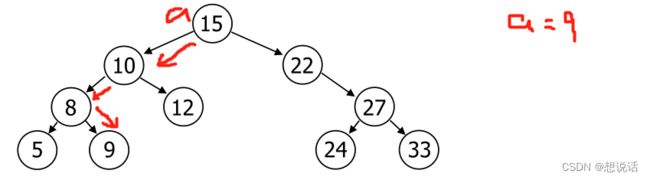
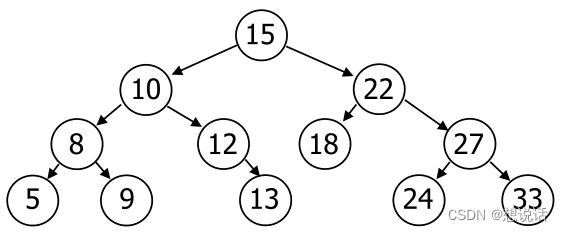
好的，我们现在清楚了基本概念了，做一个判断题，这个二叉树是不是balanced BST？

很明显，这不是一个balanced BST，在点22处发生了不平衡现象，下面的这颗二叉树才是balanced

深度为n的二叉树，针对平衡二叉树，最多能容纳的结点个数为N=(2^n-1），那么如果对其进行搜索时，最多需要搜索多少次呢。想一下我们的搜索策略？很明显应该为 log2（N），在这里也就是n次！

当我们的数据量加倍，现在有2N个结点的二叉树需要我们搜索呢？次数应该为log2（N）+1次， 可以看出搜索的代价减少了很多！

现在的一切事情是不是看起来很美好啦？但是完全美好的事物中一定有挥之不去的阴影存在！
当我们对balanced BST进行 插入和删除 的时候，很有可能就导致平衡的结构发生了改变，就从balanced 变成 unbalanced了。

我们需要一种方法把unbalanced变成balanced，这样才能不断延续我们美好的搜索策略？常见的方法包含AVL方法和 Red-Black Tree 方法。我这里也给你说一下AVL方法吧，虽然PPT里面只说了红黑树。我个人认为AVL是红黑树的基础，

AVL

AVL树是一种带有自平衡功能的二叉查找树。

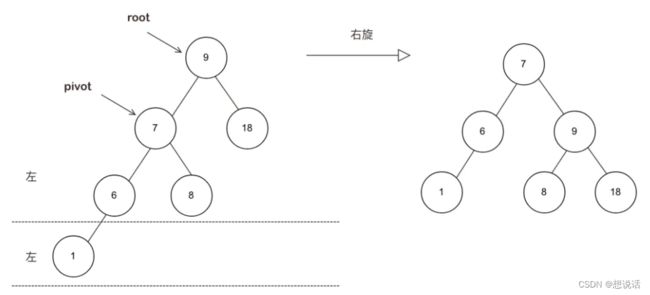
针对上面这个图，在插入key为1的节点后，变成了unbalanced。AVL通过旋转的方式完成了平衡调整。分别包括左旋和右旋。
失衡的四种场景
主要包括LL型失衡，RR型失衡，LR型失衡，RL型失衡

LL型失衡

LL型失衡：新插入结点在root的左侧，其父亲的左侧
解决这种失衡：以root的left为支点进行旋转，并且按照BST排列

RR型失衡

RR型失衡：新插入结点在root的右侧，其父亲的右侧
解决这种失衡：以root的right为支点进行旋转，并且按照BST排列

LR型失衡

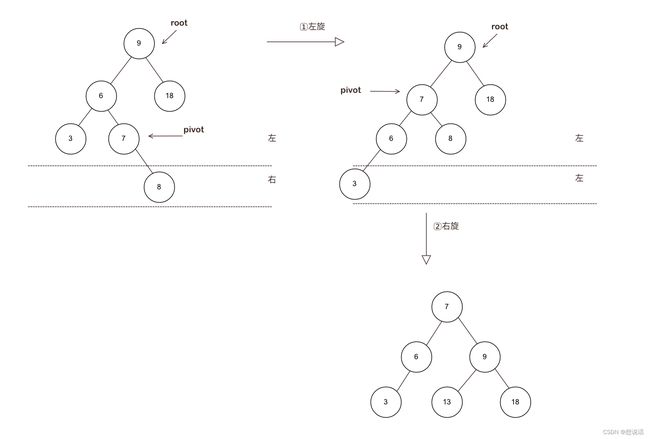
LR型失衡：新插入结点在root的左侧，其父亲的右侧
解决这种失衡：先以其父亲为支点作一次左旋，随后进行一次右旋。

RL型失衡

RL型失衡：新插入结点在root的右侧，其父亲的左侧
解决这种失衡：先以其父亲为支点作一次右旋，随后进行一次左旋。

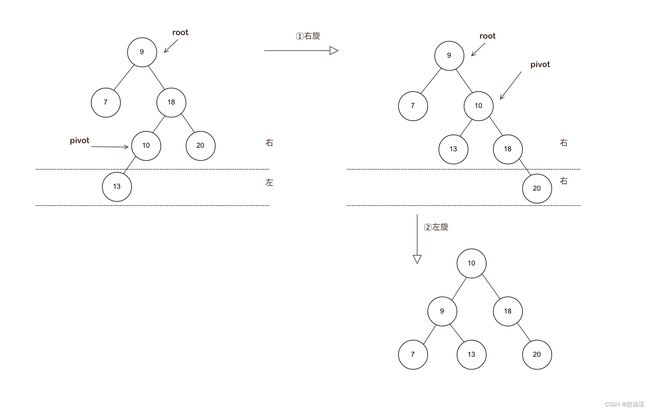
二叉树的失衡无外乎以上四种情况，针对由插入和删除导致的任何不平衡问题。
可以对其进行判别，重复进行旋转，获得一棵平衡的二叉树。
但是不可避免，要花很长的时间应用于二叉树调整。
搜索时间复杂度O（logn）

Red-Black

红黑树的特点

1. 每个节点是红色/黑色的
2. 根节点是黑色的，叶子结点也是黑色的
3. 红色节点的父节点是黑色的
4. 从任一节点到叶子节点的所有路径，经过的黑色节点数量相同(black height)
   红黑树可以没有红色点
   在进行插入操作的时候，将新插入的节点设置为红色。设置为红色的原因：设置为黑色很可能会导致（4）的破坏，导致黑色节点数量不同。

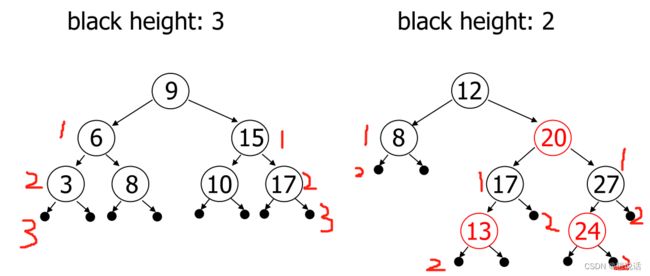
你看一下上面这个图的第二个图，很容易就看的出来：这并不是一棵balanced BST。那是不是和我们的原则相违背了呢？
其实不是这样的，红黑树的平衡条件，是以黑色高度来进行约束的。只需要满足黑色高度相等，就认为达到了黑色完美平衡。

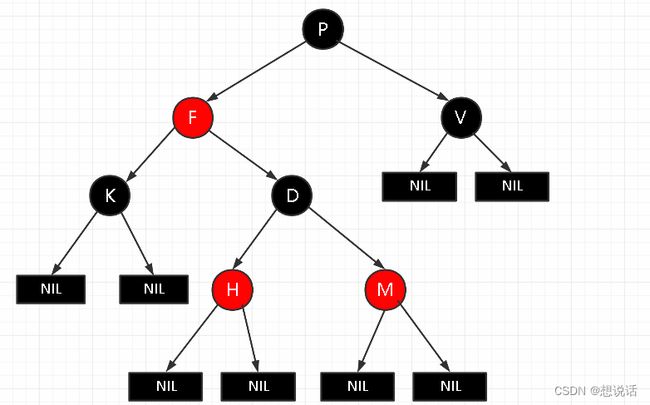
恢复平衡操作

当进行插入/删除操作的时候，很有可能导致红黑树的平衡被破坏。
回复平衡的操作包括：
1.变色：节点由红色变为黑色，或者黑色变为红色
2.右旋

3.左旋

插入节点分析

场景一：红黑树为空树

将插入节点作为红黑树的根节点，同时将其设置为黑色。

场景二：插入节点的父节点为黑色

新插入的节点为红色，父节点为黑色，因此可以直接插入，无需自平衡。

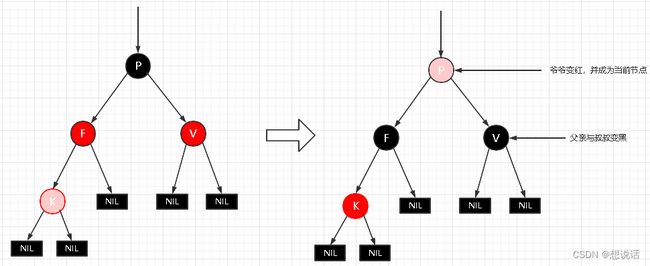
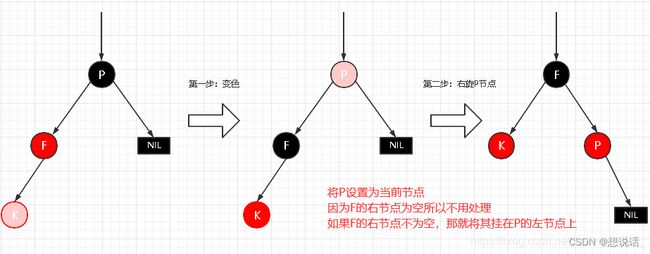
场景三：插入节点的父节点和叔叔节点为红色

将父亲（F）和叔叔（V）节点变为黑色
将爷爷§节点设置为红色（为了确保左右黑色高度相等）
如果爷爷节点（P）为根节点，再把根节点设置为黑色。
如果P不为根节点，且P的父节点为红色，继续进行自平衡处理。直到整体平衡

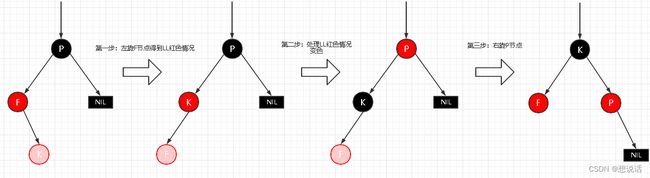
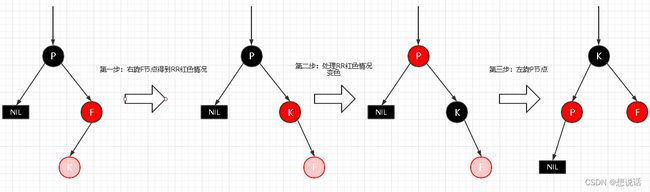
场景四：插入节点的父节点为红色，叔叔节点为黑色，父亲节点为爷爷节点的左节点

1. LL失衡

1. P设置为红色，F设置为黑色
2. 对F进行右旋
   

2. LR失衡

1. 进行一次左旋，针对K
2. 随后重复LL失衡操作
   

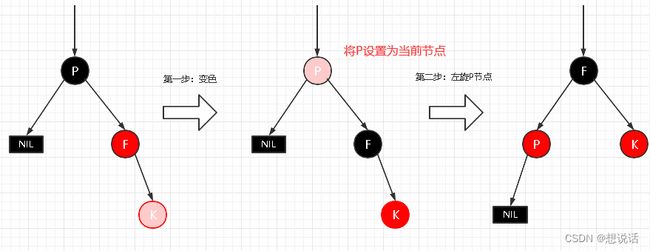
场景五：插入节点的父节点为红色，叔叔节点为黑色，父亲节点为爷爷节点的右节点

1. RR失衡

1. P设置为红色，F设置为黑色
2. 对F进行左旋
   
   2. RL失衡
3. 对F进行右旋
4. 按照RR失衡处理
   

以上就是所有的插入操作了！

思考以下几个问题：
1.红黑树特点
2.红黑树相比较AVL的优势：允许内部不平衡，减少了部分的旋转操作
3.红黑树恢复平衡操作
4.红黑树如何实现插入操作

Day7-part2

Heaps, Priority Queues 堆，优先级队列

堆

堆是一种类似于完全二叉树的数据结构，长得和完全二叉树一个样子。
最小堆：根节点值最小，父亲节点值小于子节点值
最大堆：根节点值最大，父亲节点值大于子节点值

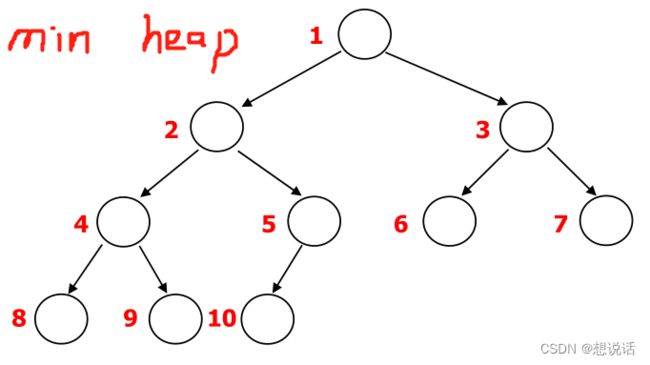
在这种存储方式下，针对节点 i
左节点 2i 右节点 2i+1 父亲节点 i//2

实现方法

1. 很直观来看，我们可以用二叉树来实现堆
   但是存在一些问题，第一个是针对二叉树，其构造依赖于技巧，同时在增添节点时不容易增加。
2. 还可以通过列表来实现堆，美中不足的是，不要忘记列表从0开始索引。
   
   接下来，我们的讨论均针对最小堆

增添操作

在最小堆中我们增加一个元素6

很显然，目前的状态是不满足最小堆的性质的。
我们需要将6进行合理的排列，怎么做呢？
最小堆的性质：父亲节点的值应小于当前结点的值 我们是不是逐步向前比较就好了？
6和40比较，6<40，随后交换位置
6和11比较，6<11，随后交换位置
6和8比较，6<8，随后交换位置
最终完成排列

pop最小值操作

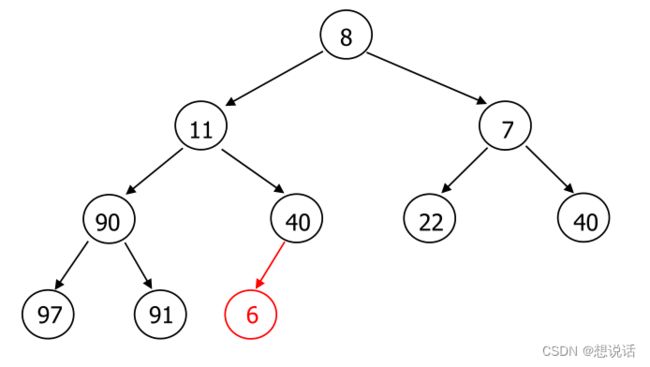
我们想把堆中的最小值取出来，并且堆仍然满足最小堆的条件！

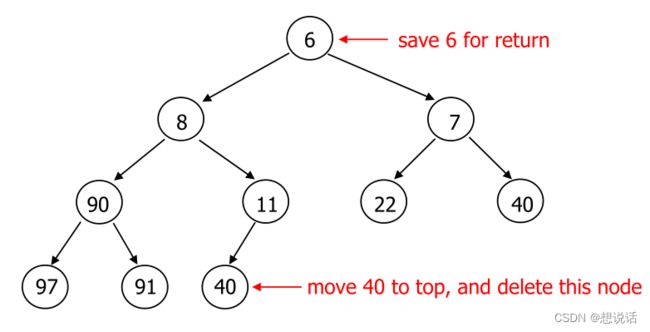
首先最小值很好取，肯定就是nums[ 0 ]，我们把这个值保存下来，最后return出来就好了
关键是如何满足最小堆的条件？
将nums[ 0 ] 和最后一个节点（40）交换位置，再将最后一个节点删除。
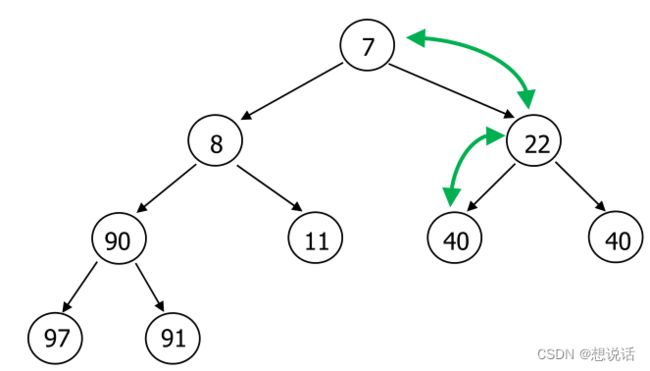
随后按照性质，把root节点放在合适的位置
40和7比较，7<40，随后交换位置
40和22比较，22<40，随后交换位置

代码实现

class heap:
    def __init__(self,nums=[]):
        self.nums=[]
        if nums:
            self.buildheap(nums)

    def isempty(self):
        return not self.nums

    def buildheap(self,nums):
        for x in nums:
            self.insert(x)

    def insert(self,a):
        self.nums.append(a)
        cur=len(self.nums)-1
        while(cur>0):
            if a<self.nums[(cur-1)//2]:
                self.nums[cur],self.nums[(cur-1)//2]=self.nums[(cur-1)//2],self.nums[cur]
                cur=(cur-1)//2
            else:
                break
    def sift_down(self,cur):
        while(cur<=len(self.nums)//2):
            left=2*cur+1
            right=2*cur+2
            if left >len(self.nums)-1:
                break
            elif left<len(self.nums) and right<len(self.nums):
                if self.nums[cur]>self.nums[left]:
                    self.nums[cur],self.nums[left]=self.nums[left],self.nums[cur]
                    cur=left
                    continue
                elif self.nums[cur]>self.nums[right]:
                    self.nums[cur],self.nums[right]=self.nums[right],self.nums[cur]
                    cur=right
                    continue
                else:
                    break
            else:
                if self.nums[cur]>self.nums[left]:
                    self.nums[cur],self.nums[left]=self.nums[left],self.nums[cur]
                    cur=left
                else: break

    def remove(self):
        result=self.nums[0]
        self.nums[0],self.nums[len(self.nums)-1]=self.nums[len(self.nums)-1],self.nums[0]
        self.nums.pop()
        self.sift_down(0)
        return result

h=heap([1,2,3,7,8,5,3])
h.remove()
print(h.nums)

优先级队列

数据带有优先级，一般出队列时，可能需要优先级高的元素先出队列。
通过堆实现
具体的PPT也没说掌握到什么，我也就先不看了哦！

总结

这一部分什么最重要？
概念的理解最重要
红黑树的性质？红黑树如何恢复平衡？红黑树插入操作？
堆的性质？如何实现？
加油宝贝，我相信你可以的！

• 尚想旧情怜婢仆，也曾因梦送钱财。 诚知此恨人人有，贫贱夫妻百事哀。

参考：https://blog.csdn.net/crazymakercircle/article/details/125017316