leetcode：1143. 最长公共子序列
题目来源
- leetcode
题目描述
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
}
};
题目解析
什么是最长公共子序列
最长公共子序列的问题常用于解决字符串的相似度，是一个非常实用的算法
首先，让我们先来看一下子串、子序列还有公共子序列的概念
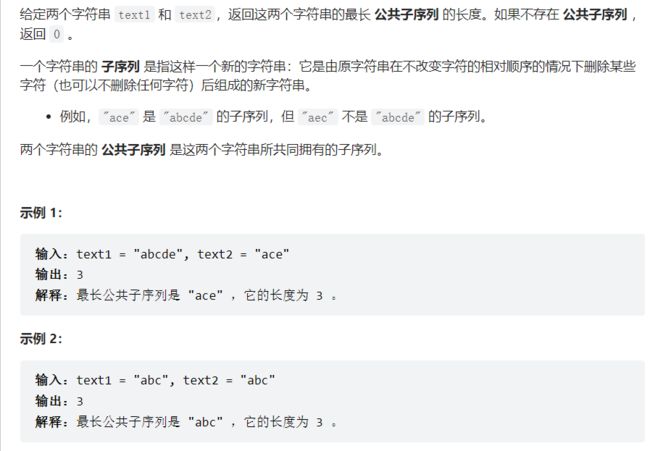
- 子串：指的是字符串中连续的n个字符，如abcdefg中，ab，cde，fg等都属于它的字串。
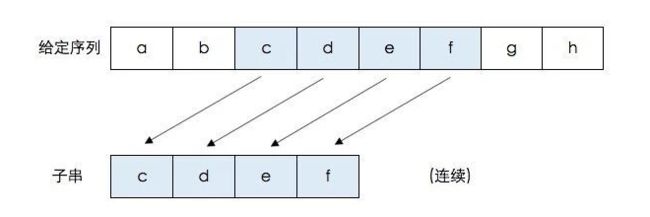
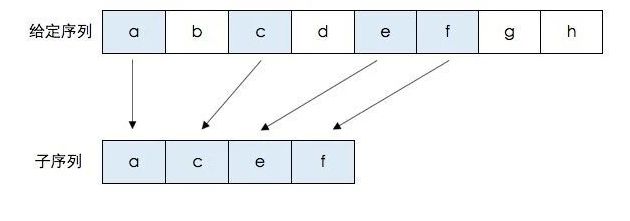
- 子序列：指的是字符串中不一定连续但先后顺序一致的n个字符，即可以删除字符串中的部分字符，但不可改变其前后顺序。如abcdefg中，acdg，bdf属于它的子序列，而bac，dbfg则不是，因为它们与字符串的字符顺序不一致。
- 公共子序列：如果序列C既是序列A的子序列，同时也是序列B的子序列，则称它为序列A和序列B的公共子序列。如对序列 1,3,5,4,2,6,8,7和序列 1,4,8,6,7,5 来说，序列1,8,7是它们的一个公共子序列。
那么现在，我们再通俗的总结一下最长公共子序列（LCS）：就是A和B的公共子序列中长度最长的（包含元素最多的）
仍然用序列1,3,5,4,2,6,8,7和序列1,4,8,6,7,5为例，它们的最长公共子序列有1,4,8,7和1,4,6,7两种，但最长公共子序列的长度是4。由此可见，最长公共子序列（LCS）也不一定唯一。
第三个版本
举个例子：找规律
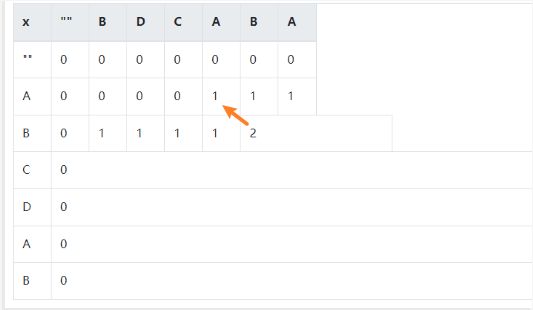
（1）准备一个表
- 因为是“子序列”，它可以删除多个或者零个，也可以全部干掉。因此我们的第一个子序列为空字符串
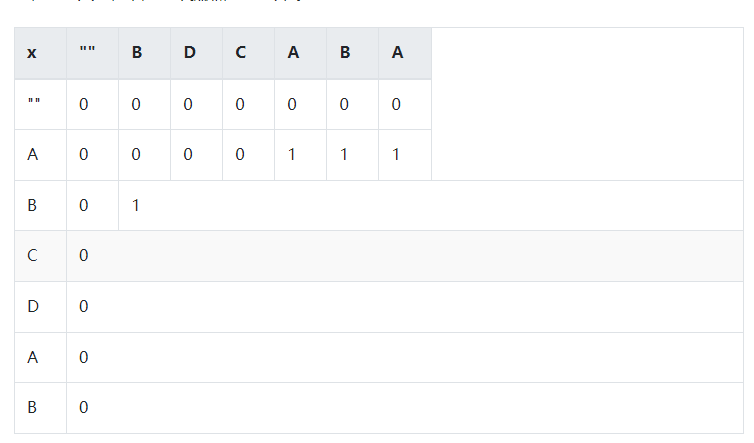
- 假设当前X ＝ “ABCDAB”， Y＝"BDCABA"，我们总是从左到右比较，因此画出表格如下
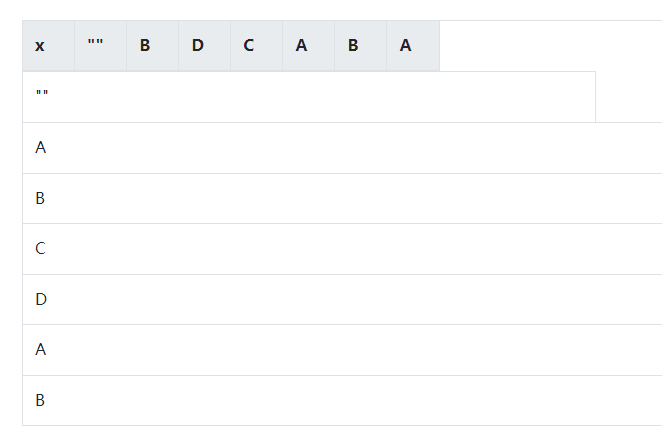
（2）对于X ＝ “ABCDAB”， Y＝"BDCABA"，各自取出最短的序列，也就是空字符串和空字符串比较。此时两个空字符串的公共区域的长度为0
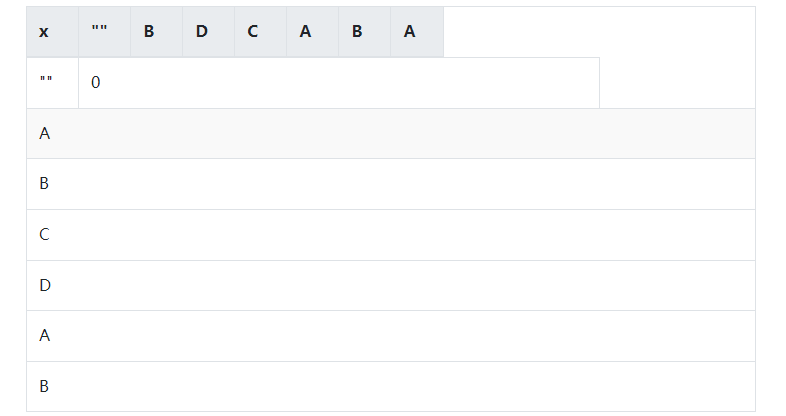
（3）然后我们X不动，继续让空字符串出阵，Y让“B”出阵，很显然，它们的公共区域的长度为0. Y换成其他字符， D啊，C啊， 或者， 它们的连续组合DC、 DDC， 情况没有变， 依然为0. 因此第一行都为0. 然后我们Y不动，Y只出空字任串，那么与上面的分析一样，都为0，第一列都是0.
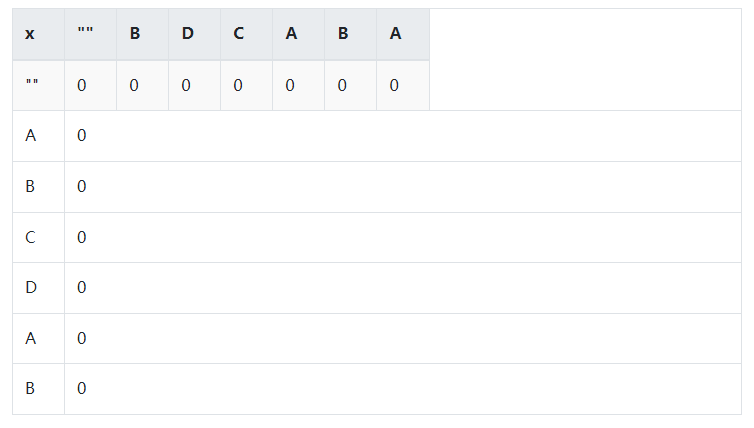
LCS问题与背包问题有些不一样，背包问题还可以设置-1行，而最长公共子序列因为有空子序列的出现，一开始就把左边与上边固定死了。
（4）然后我们把问题放大些，这次双方都出一个字符，显然只有两者都相同时，才存在不为空字符串的公共子序列，长度此时为1。
如下，A为"X", Y为"BDCA"的子序列的任意一个
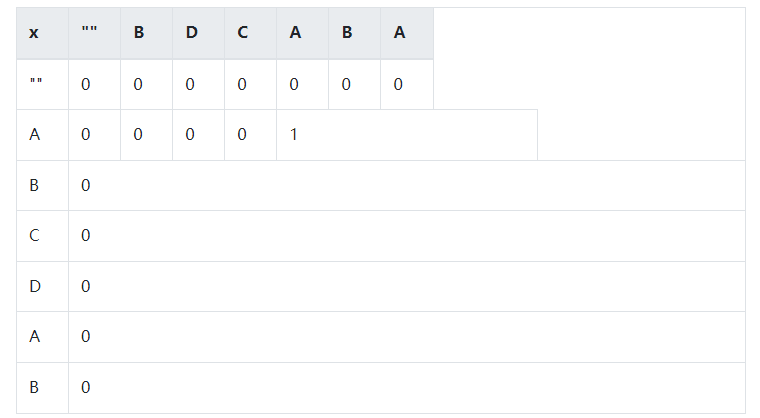
继续往右填空，该怎么填？显然，LCS不能大于X的长度，Y的从A字符串开始的子序列与B的A序列相比，怎么也能等于1。（只要一个序列只有一个字符，那么另一个序列无论多长，它们的最长公共子序列长度最多只能为1）
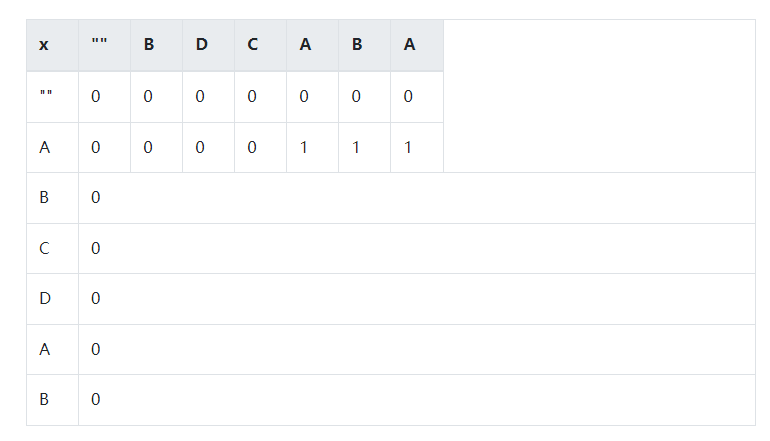
（5）如果X只从派出前面个字符A,B，亦即是“”，“A”, “B”, "AB"这四种组合，
- 前两个已经填好了。
- 那我们先看B， X [ 1 ] = = Y [ 0 ] X[1] == Y[0] X[1]==Y[0]， 显然我们得到一个新的公共子串了，应该加1。为什么呢？因为我们这个矩阵是一个状态表，从左到右，从上到下描述状态的迁移过程，并且这些状态是基于已有状态累加出来的。现在我们需要确认的是，现在我们要填的这个格子的值与它周围已经填好的格子的值是存在何种关系。目前，信息太少，就是一个孤点，直接填1。
（6）
- 然后我们让Y多出一个D做帮手，
{"",A,B,AB} VS {"",B,D,BD}，显然，继续填1. - 然后我们让Y多出一个C做帮手，
{"",A,B,AB} VS {"",B,D,BD, C, BC, DC, BDC}，显然，继续填1. - 然后我们让Y多出一个A做帮手，
{"",A,B,AB} VS {"",B,D,BD, C, BC, DC, BDC, A, BA, DA, BDA, CA, BCA, DCA, BDCA}，显然，继续填1. - 可以看出，一直填到Y的第二个B之前，都是1。 而到了BDCAB时，它们有另一个公共子序列，AB。
- 这个2是根据左上角的1推导出来的。很显然去除B这个公共字符之后，两个字符串还剩下A、BDCA（原来是AB，BDCAB），就是其左上角已经填过的组合
（7）Y将所有字符派上去，X依然是2个字符，经仔细观察，还是填2.
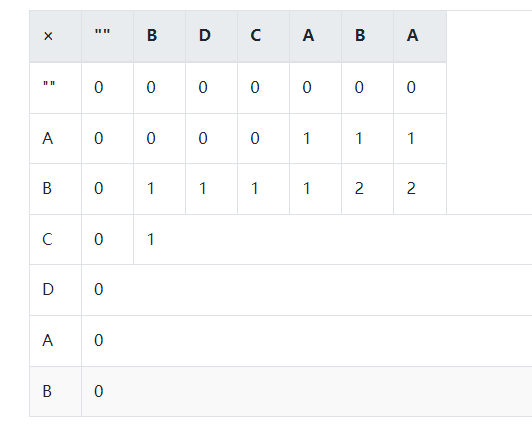
X再多派一个C，ABC的子序列集合比AB的子序列集合大一些，那么它与Y的B子序列集合大一些，就算不大，就不能比原来的小。显然新增的C不能成为战力，不是两者的公共字符，因此值应该等于AB的子序列集合。
这时我们可以确定，如果两个字符串要比较的字符不一样，那么要填的格子是与其左边或上边有关，那边大就取那个。
如果比较的字符一样呢，稍安毋躁，刚好X的C要与Y的C进行比较，即ABC的子序列集合{“”,A,B,C,AB,BC,ABC}与BDC的子序列集合｛“”,B,D,C,BD,DC,BDC｝比较，得到公共子串有“”,B,C 。这时还是与之前的结论一样，当字符相等时，它对应的格子值等于左边/右边/左上角的值 + 1，并且左边，上边，左上边总是相等的。这些奥秘需要更严格的数学知识来论证。
-
假设有两个数组，A和B。A[i]为A的第i个元素，A(i)为由A的第一个元素到第i个元素所组成的前缀。m(i, j)为A(i)和B(j)的最长公共子序列长度。
-
由于算法本身的递推性质，其实只要证明，对于某个i和j：
- m(i, j) = m(i-1, j-1) + 1 （当A[i] = B[j]时）
- m(i, j) = max( m(i-1, j), m(i, j-1) ) （当A[i] != B[j]时）
-
第一个式子很好证明，即当A[i] = B[j]时。可以用反证，假设m(i, j) > m(i-1, j-1) + 1 （m(i, j)不可能小于m(i-1, j-1) + 1，原因很明显），那么可以推出m(i-1, j-1)不是最长的这一矛盾结果。
-
第二个有些trick。当A[i] != B[j]时，还是反证，假设m(i, j) > max( m(i-1, j), m(i, j-1) )。
-
由反证假设，可得m(i, j) > m(i-1, j)。这个可以推出A[i]一定在m(i, j)对应的LCS序列中（反证可得）。而由于A[i] != B[j]，故B[j]一定不在m(i, j)对应的LCS序列中。所以可推出m(i, j) = m(i, j-1)。这就推出了与反正假设矛盾的结果。
-
得证。
我们现在用下面的方程来继续填表了。
简单来说，填写table[i][j]的规律就是：相等左上角+1，不等取上或者右最大值，如果上、左一样大，那么优先取左
思路二
比如下面，想要求s1和s2的最长公共子序列，不妨称这个子序列为 lcs。那么对于 s1 和 s2 中的每个字符，有什么选择？很简单，两种选择，要么在 lcs 中，要么不在。
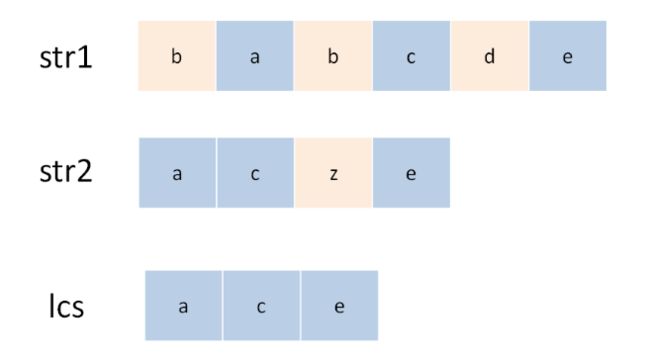这个「在」和「不在」就是可能性。很明显可以看出，如果某个字符应该在lcs中，那么这个字符肯定同时存在于s1和s2中，因为lcs是最长公共子序列呀。
所以可以这样做：
- 用两个指针
i和j从后往前遍历s1和s2，如果s1[i] == s2[j]，那么这个字符一定在lcs中。否则，s1[i]和s2[j]这两个字符至少有一个不在lcs中，需要丢弃一个。 - 对于第一种情况，找到一个 lcs 中的字符，同时将 i j 向前移动一位，并给 lcs 的长度加一；对于后者，则尝试两种情况，取更大的结果。
def longestCommonSubsequence(str1, str2) -> int:
def dp(i, j):
# 空串的 base case
if i == -1 or j == -1:
return 0
if str1[i] == str2[j]:
# 这边找到一个 lcs 的元素，继续往前找
return dp(i - 1, j - 1) + 1
else:
# 谁能让 lcs 最长，就听谁的
return max(dp(i-1, j), dp(i, j-1))
# i 和 j 初始化为最后一个索引
return dp(len(str1)-1, len(str2)-1)
问题：对于 s1[i] 和 s2[j] 不相等的情况，至少有一个字符不在 lcs 中，会不会两个字符都不在呢？比如下面这种情况：
所以代码是不是应该考虑这种情况，改成这样：
if str1[i - 1] == str2[j - 1]:
# ...
else:
dp[i][j] = max(dp[i-1][j],
dp[i][j-1],
dp[i-1][j-1])
可以是可以，但是多此一举，因为 dp[i-1][j-1] 永远是三者中最小的，max 根本不可能取到它。
小结一下
定义子问题table[i][j]为字符串A的第一个字符到第i个字符和字符串B的第一个字符到第j个字符串的最长公共子序列。 如A为“app”,B为“apple”，table[ 2 ][ 3 ]表示 “ap” 和 “app” 的最长公共字串。
- 当我们要求table[ i ][ j ]，我们要先判断A[ i ]和B[ j ]是否相同，如果相同他就是table[ i - 1 ][ j - 1 ] + 1，相当于在两个字符串都去掉一个字符时的最长公共字串再加 1；
- 否则最长公共字串取table[ i ][ j - 1 ] 和table[ i - 1 ][ j ] 中大者
class LCS {
public:
int findLCS(string A, int n, string B, int m) {
// write code here
int table[n + 1][m + 1];
for(int i = 0;i <= n;++i)table[i][0] = 0;
for(int i = 0;i <= m;++i)table[0][i] = 0;
for(int i = 0;i < n;++i){
for(int j = 0;j < m;++j){
if(A[i] == B[j])
table[i + 1][j + 1] = table[i][j] + 1;
else {
table[i + 1][j + 1] = max(table[i][j + 1],table[i + 1][j]);
}
}
}
return table[n][m];
}
};
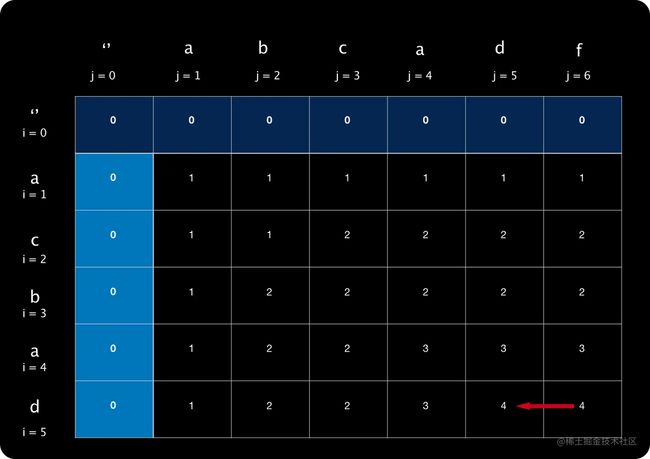
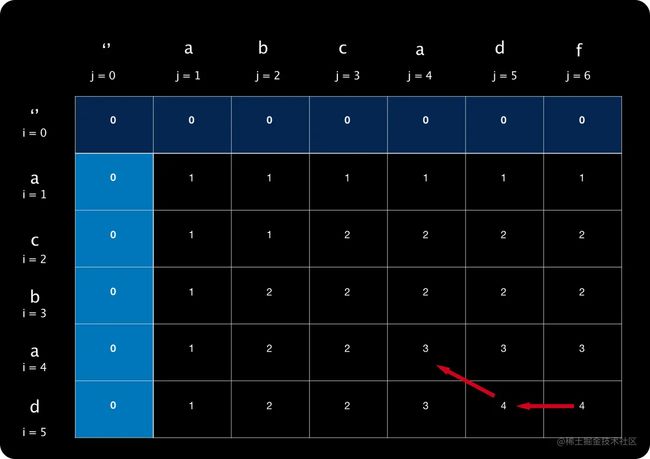
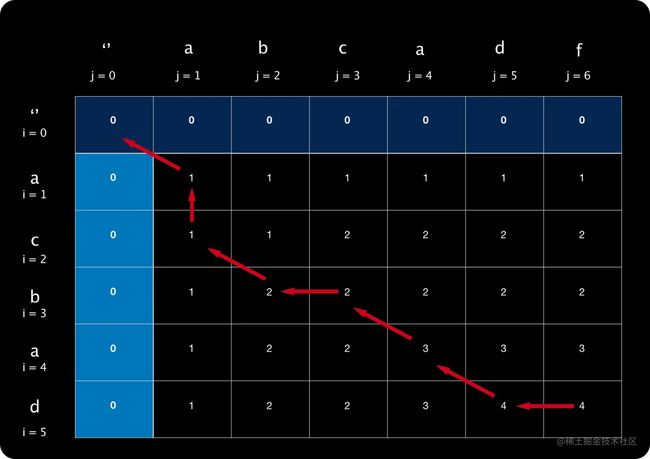
扩展：如何打印出子串呢？
我们完成填表后，只能求出最长公共子序列的长度，但是无法得知它的具体构成。我们可以从填表的反向角度来寻找子序列。
我们子序列保存在名为 s的数组中，从表格中反向搜索，找到目标字符后，每次都把目标字符插入到数组最前面。
根据前面提供的填表口诀，我们可以反向得出寻找子序列的口诀： 如果T[i][j]来自左上角加一，则是子序列，否则向左或上回退。如果上左一样大，优先取左。
- 从右下角开始分析，T[5][6]=4，它并不是来自左上角。它左边的值比上方大，所以它来自左边，向左回退，如下图箭头。
- 接着就定位到 T[5][5]，显然他来自左上角加1，它是子序列。插入数组中，有
s = ['d']
- 扣除掉 T[5][5]，可以定位到它的左上角 T[4][4]，如图：
T[4][4]也是来自左上角加1，它也是子序列，把它插入到数组最前面，此时 s 应该是
s = ['a','d']
- 按照前面的思路，继续定位分析，最终如下图：
最终箭头指向0，搜索结束。
s = ['a','b','a','d']
伪代码：
if(input1[i] == input2[j]){
s.insertToIndexZero(input1[i]); //插入到数组最前面
i--;
j--;
}else{
//向左或向上回退
if(T[i-1][j]>T[i][j-1]){
//向上回退
i--;
}else{
//向左回退
j--;
}
}
扩展：打印全部LCS
第二个版本
暴力递归
现在我们只关心 s t r 1 [ 0... i ] ， s t r 2 [ 0... j ] str1[0...i]，str2[0...j] str1[0...i]，str2[0...j]，对于它们的最长公共子序列长度是多少。
int process(std::string str1, std::string str2, int i, int j);
因此，主函数应该这样调用：
return process(str1, str2, str1.size() - 1, str2.size() - 1);
那么，这个递归函数应该怎么实现呢？我们来分析当前位置的可能性（可能做出的决策）。
（1） 如果i == 0 && j == 0：然后str1[1] == str2[j] ? 1 : 0
（2）如果i == 0时，也就是str1只有一个字符的时候
- 如果
str1[i] == str2[j]时，那么返回1 - 如果
str1[i] != str2[j]时，此时有没有str2[j]都一样，所以我们丢弃strs[j]，那么返回process(str1, str2, i, j - 1);
（3） 如果j == 0时，也就是str2只有一个字符的时候
- 如果
str1[i] == str2[j]时，那么返回1 - 如果
str1[i] != str2[j]时，那么返回process(str1, str2, i-1, j );
（4） 如果i != 0 && j != 0：
- 样本对应模型，往往以考虑结尾来组织可能性
- a) 最长公共子序列，一定不以str1[i]字符结尾、也一定不以str2[j]字符结尾
- b) 最长公共子序列，可能以str1[i]字符结尾、但是一定不以str2[j]字符结尾
- c) 最长公共子序列，一定不以str1[i]字符结尾、但是可能以str2[j]字符结尾
- d) 最长公共子序列，必须以str1[i]字符结尾、也必须以str2[j]字符结尾，此时必须strs[i] == strs[j]（避免死循环）
- 注意：a)、b)、c)、d)并不是完全互斥的，他们可能会有重叠的情况
- 但是可以肯定，答案不会超过这四种可能性的范围
- 那么我们分别来看一下，这几种可能性怎么调用后续的递归。
- a) 最长公共子序列，一定不以str1[i]字符结尾、也一定不以str2[j]字符结尾
- 如果是这种情况，那么有没有str1[i]和str2[j]就根本不重要了，因为这两个字符一定没用啊
- 所以砍掉这两个字符，最长公共子序列 = str1[0…i-1]与str2[0…j-1]的最长公共子序列长度(后续递归)
- b) 最长公共子序列，可能以str1[i]字符结尾、但是一定不以str2[j]字符结尾
- 如果是这种情况，那么我们可以确定str2[j]一定没有用，要砍掉；但是str1[i]可能有用，所以要保留
- 所以，最长公共子序列 = str1[0…i]与str2[0…j-1]的最长公共子序列长度(后续递归)
- c) 最长公共子序列，一定不以str1[i]字符结尾、但是可能以str2[j]字符结尾
- 跟上面分析过程类似，最长公共子序列 = str1[0…i-1]与str2[0…j]的最长公共子序列长度(后续递归)
- d) 最长公共子序列，必须以str1[i]字符结尾、也必须以str2[j]字符结尾
- 可能性d)存在的条件，一定是在str1[i] == str2[j]的情况下，才成立的
- 所以，最长公共子序列总长度 = str1[0…i-1]与str2[0…j-1]的最长公共子序列长度(后续递归) + 1(共同的结尾)
- a) 最长公共子序列，一定不以str1[i]字符结尾、也一定不以str2[j]字符结尾
- 综上，四种情况已经穷尽了所有可能性。四种情况中取最大即可
- 其中b)、c)一定参与最大值的比较，
- 当str1[i] == str2[j]时，a)一定比d)小，所以d)参与
- 当str1[i] != str2[j]时，d)压根不存在，所以a)参与
- 但是再次注意了！
- a)是：str1[0…i-1]与str2[0…j-1]的最长公共子序列长度
- b)是：str1[0…i]与str2[0…j-1]的最长公共子序列长度
- c)是：str1[0…i-1]与str2[0…j]的最长公共子序列长度
- a)中str1的范围 < b)中str1的范围，a)中str2的范围 == b)中str2的范围
- 所以a)不用求也知道，它比不过b)啊，因为有一个样本的范围比b)小！
- a)中str1的范围 == c)中str1的范围，a)中str2的范围 < c)中str2的范围
- 所以a)不用求也知道，它比不过c)啊，因为有一个样本的范围比c)小
- 至此，可以知道，a)就是个垃圾，有它没它，都不影响最大值的决策
- 所以，当str1[i] == str2[j]时，b)、c)、d)中选出最大值
- 当str1[i] != str2[j]时，b)、c)中选出最大值
实现：
class Solution {
int process(string &text1, string &text2, int i, int j){
if(i == 0 && j == 0){
return text1[i] == text2[j] ? 1 : 0;
}else if(i == 0){
if(text1[i] == text2[j] ){
return 1;
}else{
return process(text1, text2, i, j - 1);
}
}else if(j == 0){
if(text1[i] == text2[j]){
return 1;
}else{
return process(text1, text2, i - 1, j);
}
}else{
int p1 = process(text1, text1, i - 1, j);
int p2 = process(text1, text2, i, j - 1);
int p3 = text1[i] == text2[j] ? 1 + process(text1, text2, i - 1, j - 1) : 0;
return std::max(p1, std::max(p2, p3));
}
}
public:
int longestCommonSubsequence(string text1, string text2) {
if(text1.empty() || text2.empty()){
return 0;
}
return process(text1, text2, (int)text1.size() - 1, (int)text2.size() - 1);
}
};
暴力递归改动态规划
（1）分析可变参数
int process(std::string str1, std::string str2, int i, int j);
- i的长度： 0~str1.size() - 1
- j的长度： 0~str2.size() - 1
因为有两个变化维度，所以需要一个二维数组
int dp[N][M];
（3）分析basecase和依赖
（4）最终
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
if(text1.empty() || text2.empty()){
return 0;
}
int N = text1.size(), M = text2.size();
int dp[N][M];
dp[0][0] = text1[0] == text2[0] ? 1 : 0;
for (int i = 1; i < N; ++i) {
dp[i][0] = text1[i] == text2[0] ? 1 : dp[i - 1][0];
}
for (int j = 1; j < M; ++j) {
dp[0][j] = text1[0] == text2[j] ? 1 : dp[0][j - 1];
}
for (int i = 1; i < N; ++i) {
for (int j = 1; j < M; ++j) {
int p1 = dp[i - 1 ][j];
int p2 = dp[i][j - 1];
int p3 = text1[i] == text2[j] ? 1 + dp[i - 1][j - 1] : 0;
dp[i][j] = std::max(p3, std::max(p1, p2));
}
}
return dp[N - 1][M - 1];
}
};
javascript 最长公共子序列
详解动态规划最长公共子序列–JavaScript实现