2023.04.09 学习周报

---

摘要

This week, I read a computer science related to sequential recommendation systems, It proposes a new sequential recommendation model, IDLSTM-EC, which uses the global and contextual information of the input and forget channels to capture the long-term and short-term preferences of users. In particular, the approach takes into account the relative order between the steps performed in the sequence, while ignoring important timing information. Thus, the model combines the embedded layer and coherent input with the forget gate and embedded layer to further improve efficiency and effectiveness. Experiments on data sets show that the model is superior to the most advanced baselines and can deal with data sparsity effectively. In addition, I learn about MDS dimension reduction algorithm, Markov chain and Navier-Stokes equations. Through mathematical derivation to understand MDS algorithm, through mathematical definition and transfer of probability matrix to understand the idea of Markov chain, and understand the method of solving NS equation, and a simple description of the finite element method of two core points.

本周，我阅读了一篇与顺序推荐系统相关的文章，它提出了一种新的顺序推荐模型 IDLSTM-EC，该模型利用输入和forget通道的全局信息和上下文信息来捕捉用户的长期和短期的偏好。特别是，该方法考虑了在序列中执行步骤之间的相对顺序，而忽略了重要的时间信息。因此，该模型将嵌入的layer和连贯的输入与遗忘门和嵌入的layer结合起来，以进一步提高效率和有效性。在数据集上的实验表明，该模型优于最先进的基线，可以有效地处理数据稀疏问题。此外，我学习了MDS降维算法、马尔可夫链和Navier-Stokes方程的相关内容。通过数学推导去理解MDS算法，通过数学定义和转移概率矩阵去理解马尔可夫链的思想，以及了解求解NS方程的方法，并简单地说明了有限元法的两个核心点。

---

文献阅读

1.题目

文献链接：Time-aware sequence model for next-item recommendation

2.摘要

The sequences of users’ behaviors generally indicate their preferences, and they can be used to improve next-item prediction in sequential recommendation. Unfortunately, users’ behaviors may change over time, making it difficult to capture users’ dynamic preferences directly from recent sequences of behaviors. Traditional methods such as Markov Chains (MC), Recurrent Neural Networks (RNN) and Long Short-Term Memory (LSTM) networks only consider the relative order of items in a sequence and ignore important time information such as the time interval and duration in the sequence. In this paper, we propose a novel sequential recommendation model, named Interval- and Duration-aware LSTM with Embedding layer and Coupled input and forget gate (IDLSTM-EC), which leverages time interval and duration information to accurately capture users’ long-term and short-term preferences. In particular, the model incorporates global context information about sequences in the input layer to make better use of long-term memory. Furthermore, the model introduces the coupled input and forget gate and embedding layer to further improve efficiency and effectiveness. Experiments on real-world datasets show that the proposed approaches outperform the state-of-the-art baselines and can handle the problem of data sparsity effectively.

3.简介

1）对于许多现实世界的应用程序，如听音乐和玩游戏等，用户通常会在一段时间内执行一系列动作，形成行为序列；
2）这样的行为序列可以用来发现用户的顺序模式，并预测用户的新动作，这就是顺序推荐；
3）循环神经网络（RNN）已成功应用到序列建模和下一步预测中；
4）RNN和LSTM只关注与序列中项目相关的相对顺序信息，而忽略了一些重要的序列信息；特别是，在行为序列中彼此接近的项目具有很强的相关性。

4.本文贡献

1）文章提出了一种新的next-item推荐模型，该模型能更好地利用时间序列中的重要时间信息（如间隔时间和持续时间）；
2）通过增加嵌入层和耦合输入遗忘门，进一步提高了模型的效率和有效性；
3）在真实数据集上的实验结果表明，提出的模型优于最先进的基线，可以有效地处理数据稀疏问题。

5.传统方法

文章对传统方法进行了详细的比较，各方法的优缺点如下所示：
1）Sequential pattern mining
非常有效的固定顺序模式；但失去一些不常见但重要的模式，且推荐结果覆盖率或多样性差；
2）MC models
很好地获取了序列的本地信息，但忽略了序列的全局信息；
3）Factorization machine
很好地表现了事件的内在特征，但容易受到数据稀疏性的影响；
4）Embedding model
降低了事件表示的维数，适合多种任务，但不能自适应地对序列特征进行建模；
5）RNN
非常适合对序列中的复杂的动力学建模，但依赖于序列信息，且不能长期保持用户的兴趣。

6.IDLSTM-EC

下图展示了模型如何根据用户的序列执行预测和推荐：

下图是模型的体系结构：

间隔门是基于时间间隔信息对当前事件对下一个事件的影响进行建模，持续门是基于持续时间信息对用户对各种项目的长期兴趣进行建模，间隔门Ik和持续门Dk的定义如下：

在LSTM模型的基础上，增加间隔门Ik和持续门Dk，定义如下：

1）Adding the embedding layer
模型只使用了部分上下文信息，而没有利用全局上下文。因此，为了融合更多的上下文信息，在输入后增加嵌入层，将原始的one-hot vector转换为one-hot vectors，可以有效地捕获训练数据中项目的重要特征及其关系。其中，GloVe方法用于训练嵌入向量，它是一种常用的嵌入方法，它通过无监督学习得到向量。与其他嵌入方法不同，GloVe模型结合了全局信息和上下文来捕获更重要的信息。
2）coupling input and forget gates
采用耦合输入和遗忘门减小了模型的参数：

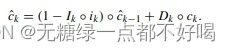
采用耦合输入和遗忘门，可以减少模型参数，提高了模型的效率。同时，参数的减少在一定程度上防止模型过拟合。

7.实验

7.1 数据集

7.2 基线

文章采用两种推荐方法作为基准，其中包括通用推荐模型和基于顺序的推荐模型：
POP、UBCF、BPR、FPMC、Session-RNN、Peephole-LSTM、Peephole-LSTM with time、Time-LSTM

7.3 评估指标

1）Recall：

2）MRR：
MRR（平均倒数排名）是一种排名评估指标，表示推荐列表中目标项目倒数排名的平均值。

模型和基线的Recall和MRR如下：

7.4 实验结果

1）不同数量的细胞单位对对一个epoch的Recall@10, MRR@10和时间的影响：

细胞单元的最佳数量是128，这会让模型能够捕获最重要的信息。
2）不同嵌入单元数量对一个epoch的Recall@10、MRR@10和时间的影响：

嵌入层中有足够的单元，以保证推荐模型中序列信息得到很好的保存，但过多的单元可能会导致过拟合。因此，嵌入层单元数设置为128个。
3）将使用不同稀疏度数据的不同模型进行比较：

实验结果显示，文章提出的方法可以有效地处理不同稀疏度的数据。

8.结论

1）作者提出了一种新颖的时间感知序列建模方法，并将其应用于下一个新项目的推荐中；
2）文章提出的方法引入了两个门，即用于建模用户偏好的持续时间门和用于建模当前项目对序列中下一个项目影响的间隔门；
3）作者采用GloVe方法利用全局上下文信息，通过耦合输入和遗忘门进一步提高其效率。

9.展望

1）作者将尝试利用注意力机制从序列中提取关键特征及其相关性；
2）作者将尝试增强模型的能力，以适应不同偏好的用户；
3）作者将考虑整合文本和描述等内容信息，以进一步提高顺序推荐的性能。

MDS降维算法

MDS降维算法要解决的问题是：给定n个对象之间的相似性，确定这些对象在低维空间中的表示，并使其尽可能与原先的相似性大致匹配。

高维空间中每一个点代表一个对象，因此点与点之间的距离和对象之间的相似度高度相关。也就是说，两个相似的对象在高维空间中由两个距离相近的点表示，两个不相似的对象在高维空间中由两个距离比较远的点表示。

1.基本思想

将高维空间中的点投影到低维空间中，并保持点与点之间的相似性尽可能不变，即希望降维前后能够保持距离关系不变，从而能够很好地进行可视化。

2.优化目标

考虑将原始数据矩阵X∈R^ d*m降维成Z∈R^ d’*m，其中m是样本点的个数，原始数据是d维，希望将其降到d’维。

现在要找到m个d’维的向量，zi, i = 1, 2, …, m，使其能满足以下这个优化的条件：

其中：dij表示原始样本i和原始样本j之间的距离，需要满足以下三个条件。
1）自身与自身距离为0，即dii = 0；
2）对称性，即dij = dji；
3）三角不等式，dik + djk >= dij。

3.数学推导

现在这个优化问题的解并不是唯一的，需要我们加上一个约束（中心化）：

这是因为，若我们求得问题的解为zi*, i = 1, 2, …, m，然后将其平移任意单位后得到 zi hat = zi - z0, i = 1, 2, …, m。如下所示：

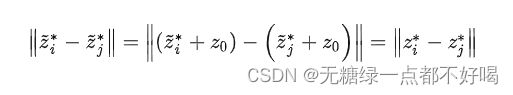
于是，根据上述条件求解这个优化问题：

通过求解方程组，我们就确定并得到矩阵B的所有元素，然后通过特征分解方法就可以得到矩阵Z。

4.算法流程

1）根据给定的原始数据和距离度量方法，计算出原始空间中数据点的距离矩阵D；
2）计算得到四个变量，T1，T2，T3，T4；
3）利用公式求得矩阵B的元素，bij = -1/2 T1 + 1/(2m) T2 + 1/(2m) T3 - 1/(2mm) T4；
4）将B进行特征分解得到特征值，以及对应的特征向量；
5）取特征值矩阵最大的前Z项及其对应的特征向量，得到降维后的矩阵Z。

马尔可夫链

马尔可夫链的思想：过去所有的信息都已经被保存到现在的状态，基于现在的状态就可以预测未来。

1.随机过程

简单来说，随机过程就是使用统计模型一些事物的过程进行预测和处理。比如：股价预测，通过今天股票的涨跌，预测明天后天股票的涨跌；天气预报，通过今天是否下雨，预测明天后天是否下雨。这些过程都是可以利用数学公式进行计算的，随机过程就是这样一个工具，把整个过程进行量化处理。通过是否下雨、股票涨跌的概率，用公式就可以推导出来N天后的状况。

2.简介

马尔科夫链为状态空间中经过从一个状态到另一个状态转换的随机过程，该过程要求下一个状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这是因为马尔科夫链认为过去所有的信息都被保存在当前状态中。

比如：现在有一串数列1, 2, 3, 4, 5, 6，在马尔科夫链的角度来看，6的状态只与5有关，与前面的其它过程无关。

3.数学定义

假设序列为…, Xt-2, Xt-1, Xt, Xt+1, …，那么在Xt+1状态的条件概率仅依赖于前一刻的状态Xt，即P(Xt+1 | …, Xt-2, Xt-1, Xt) = P(Xt+1 | Xt)。

综上所述，我们可以知道某一时刻状态转移的概率只依赖于它的前一个状态 ，那么我们只要求出系统中任意两个状态之间的转换概率，就可以求得马尔科夫链的模型。

4.转移概率矩阵

通过马尔科夫链的模型，我们可以将事件的状态转换成概率矩阵：

上图中有A和B两个状态，A -> A的概率是 0.3，A -> B的概率是 0.7；B -> B的概率是 0.1，B -> A的概率是 0.9。

问题1：初始状态为A，求两次运动后状态为A的概率是多少？
P = 0.30.3 + 0.70.9 = 0.72
问题2：当初始状态和终止状态未知时，求两次运动后的状态概率分别是多少？
引入状态转移概率矩阵：

结论：
初始状态为A，两次运动后状态为A的概率是 0.72；
初始状态为A，两次运动后状态为B的概率是 0.28；
初始状态为B，两次运动后状态为A的概率是 0.36；
初始状态为B，两次运动后状态为B的概率是 0.64。

综上所述，有了概率矩阵，可以求出运动n次后的各种概率。

5.状态转移矩阵的稳定性

用马尔可夫链表示股市模型，共有三种状态：牛市、熊市和横盘，其中每一个状态都以一定的概率转化为下一个状态。定义牛市为状态0， 熊市为状态1，横盘为状态2，即可以得到状态转移矩阵：
P = [ [0.7 0.175 0.125]
[0.25 0.6 0.15 ]
[0.25 0.25 0.5 ] ]
假设当前股市的概率分布为[0.4, 0.3, 0.3]，即40%概率的牛市，20%概率的熊市和30%概率的横盘。然后将这个状态作为序列概率分布的初始状态t0，将其带入这个状态转移矩阵计算t1, t2, t3, …的状态。

import numpy as np

matrix = np.matrix([[0.7, 0.175, 0.125],
                    [0.25, 0.6, 0.15],
                    [0.25, 0.25, 0.5]], dtype=float)
vector = np.matrix([[0.4, 0.3, 0.3]], dtype=float)

print(matrix)

for i in range(100):
    vector = vector * matrix
    print('当前回合: {}'.format(i + 1))
    print(vector)

输出结果：

当前回合: 1
[[0.43  0.325 0.245]]
当前回合: 2
[[0.4435 0.3315 0.225 ]]
当前回合: 3
[[0.449575  0.3327625 0.2176625]]
当前回合: 4
[[0.45230875 0.33274875 0.2149425 ]]
. . . . . 
当前回合: 18
[[0.45454542 0.33216786 0.21328672]]
当前回合: 19
[[0.45454544 0.33216784 0.21328672]]
当前回合: 20
[[0.45454545 0.33216784 0.21328671]]
当前回合: 21
[[0.45454545 0.33216783 0.21328671]]
当前回合: 22
[[0.45454545 0.33216783 0.21328671]]
当前回合: 23
[[0.45454545 0.33216783 0.21328671]]
. . . . . 
当前回合: 99
[[0.45454545 0.33216783 0.21328671]]
当前回合: 100
[[0.45454545 0.33216783 0.21328671]]

从第20轮开始，状态概率分布就保持不变了，[0.45454545 0.33216783 0.21328671]，即 45.5%的牛市，33.2%的熊市与21.3%的横盘。由此可得，状态转移矩阵经过一定有限次数序列的转换，最终一定可以得到一个稳定的概率分布，且与初始状态概率分布无关。

参考链接：https://zhuanlan.zhihu.com/p/38764470

Navier-Stokes方程

1.简介

通过前面的学习，了解到经典力学框架下的NS方程就是牛顿第二定律的运用。其核心本质是动量守恒，但NS方程只是一个对流体在连续介质层面的物理近似，是一个对流体在分子动力学层面进行粗粒化的物理模型。

不考虑源项和外力项，NS方程可分为：
1）不可压缩NS方程（INSE）

2）可压缩NS方程（CNSE）

由 d/dt = ∂t + uβ∂β，INSE可改写为：

即简单的牛顿第二定律F = ma。

源项：除流体自身以外的，能对流动产生影响的外源，如重力，温差，多相流中的表面张力，化学反应产生的力，MHD的磁场等。

2.求解NS方程的方法

常用的离散方法：
1）有限元类，如DG，SD/SV等；
2）有限差分，向前/向后/中心差分；
3）有限体积；
4）谱方法及其相应拓展，如谱元法等。

3.有限元法

有限元的思想是将一个复杂的连续体划分为有限个简单的离散单元，然后利用数学方法求解每个单元的物理量，最后通过组合或插值得到整个连续体的物理量。

3.1 核心思想

1）求偏微分方程的近似解：
很多问题都可以归结为一个泛函数。在弹性力学中，可以写出—个泛函数表示势能，然后解决问题的方式是找出一个函数去最小化泛函数。想要找到这个函数，就需要用到变分法，即令泛函数的—阶变分等于零，这个原理类似于找一个函数的极值是通过令它的导数等于零求出。一阶变分等于零通过分部积分后通常可分为两个部分，一个偏微分方程形式的控制方程，另一部分是边界条件。于是问题便转化为求解带有边界条件的PDE。工程中通常希望用简化的方法求解PDE的近似解，其中近似求解PDE有多种方法，他们的核心思想是设一个形式已知的近似方程(有限元中常用多项式)，然后带入原PDE或泛函数来求解未知系数。

2）离散化：
一个连续的介质会被离散成数个简单的基本几何单元，这些单元是通过节点相互联系，这个过程就是网格划分。对于每一个单元都可以用上一段的方法进行求解，然后通过节点间的联系将单元的结果组合成整个区域的结果，即assemble the stiffness matrix。

3.2 推导步骤

1） 建立微分方程模型，描述连续体的物理行为；
2）选择合适的单元类型，如线单元、面单元、体单元等，将连续体划分为有限个单元，并确定每个单元的节点和自由度；
3）选择合适的形函数，描述每个单元内部的物理量分布，如位移、温度、应力等；
4）利用变分原理或加权残差法，将微分方程模型转化为代数方程组，即有限元方程；
5）求解有限元方程，得到每个节点的物理量值；
6）利用插值或后处理方法，得到每个单元内部和整个连续体的物理量分布。

---

总结

本周，我学习了MDS降维算法、马尔可夫链和Navier-Stokes方程的相关内容；MDS降维算法的思想是给定n个对象之间的相似性，去确定这些对象在低维空间中的表示，并使其尽可能维持原先的相似性；马尔可夫链的特点是下一个状态只与当前状态有关，这是因为马尔可夫链认为过去所有的信息都已经被保存到当前的状态；我了解到求解Navier-Stokes方程的方法，由于没有系统的资料，所以本周只简单地介绍了有限元法。下周，我将对有限元法进行深入学习。