2023年中国传媒大学程序设计大赛（同步赛）

F-舞台矩形​​​​​​

思路：

1.  查询区间信息，使用线段树。线段树维护区间最高与最低点

2. 我们可以记录每个同学的x,y坐标，然后根据x对数组排序，实现离散处理。
3. 因为查询时给的是原数组信息，所以我们一个数组排序，一个保持原样。后面查询时，根据原数组查找排序后的数组对应位置即可

#include 
using namespace std;
#define ll     long long
#define int ll
typedef pair pll;
const int INF = 0x3f3f3f3f;         //int型的INF

const int N = 1e5 + 10;
int n;
struct tree
{
	int l,r;
	pll d;//pair的第一个表示高，第二个表示低
} t[N<<2];
pll a[N],b[N];
void build (int l,int r,int p)
{
	t[p].l=l,t[p].r=r;
	if (l==r)
		{
			t[p].d.first=t[p].d.second=a[l].second;
			return;
		}
	int mid=l+((r-l)>>1);
	build(l,mid,p<<1);
	build(mid+1,r,p<<1|1);
	t[p].d.first=max(t[p<<1].d.first,t[p<<1|1].d.first);
	t[p].d.second=min(t[p<<1].d.second,t[p<<1|1].d.second);
}

pll ask(int l,int r,int p)//pair返回区间最高最低
{
	if (l<=t[p].l&&t[p].r<=r)return t[p].d;
	pll tmp= {-INF,INF};
	int mid=t[p].l+((t[p].r-t[p].l)>>1);
	if (l<=mid)	tmp.first=max(tmp.first,ask(l,r,p<<1).first),tmp.second=min(tmp.second,ask(l,r,p<<1).second);
	if (r>mid)	tmp.first=max(tmp.first,ask(l,r,p<<1|1).first),tmp.second=min(tmp.second,ask(l,r,p<<1|1).second);
	return tmp;
}

pll find(int x1,int x2)//通过b数组的x值查询对应的排序后的a数组位置
{
	int l=1,r=n,ans1,ans2;
	while (l<=r)
		{
			int mid=l+((r-l)>>1);
			if (a[mid].first>=x1)ans1=mid,r=mid-1;
			else  l=mid+1;
		}
	l=1,r=n;
	while (l<=r)
		{
			int mid=l+((r-l)>>1);
			if (a[mid].first<=x2)ans2=mid,l=mid+1;
			else r=mid-1;
		}
	return {ans1,ans2};
}
int32_t main()
{

	cin>>n;
	for (int i=1; i<=n; ++i)cin>>a[i].first>>a[i].second,b[i]=a[i];
	sort(a+1,a+1+n);
	build(1,n,1);
	int q;
	cin>>q;
	int A,B;
	while (q--)
		{
			cin>>A>>B;
			int ans=b[B].first-b[A].first;
			if (ans>0)//你右-左坐标差为正数才执行，否则为0
				{
					pll t=find(b[A].first,b[B].first);
					pll	tmp=ask(t.first,t.second,1);
					ans*=tmp.first-tmp.second;
				}
			else ans=0;
			cout<

G-跳台滑雪

思路：线段树

1. 还是处理区间信息，因为分数数据只有1e6，直接线段树根据分数建立，无需离散化。然后维护区间最大概率。

2. 对于每个概率，我们记录这个概率对应的最大分数与序号即可

#include 
using namespace std;
#define ll     long long
#define int ll
const int N = 1e6 + 10;
mapmp,mp1;
int a[N];
struct tree
{
	int l,r;
	double p;
} t[N<<2];
bool cmp(int x,int y)
{
	return x>y;
}
void build(int l,int r,int p)
{
	t[p].l=l,t[p].r=r,t[p].p=0;
	if (l==r)return;
	int mid=l+((r-l)>>1);
	build(l,mid,p<<1);
	build(mid+1,r,p<<1|1);
}
void update(int x,int p,double p1)
{
	if (t[p].l==x&&t[p].r==x)
		{
			t[p].p=max(t[p].p,p1);
			return;
		}
	int mid=t[p].l+((t[p].r-t[p].l)>>1);
	if (x<=mid)update(x,p<<1,p1);
	if (x>mid)update(x,p<<1|1,p1);
	t[p].p=max(t[p<<1].p,t[p<<1|1].p);
}

double ask(int l,int r,int p)
{
	if (l<=t[p].l&&t[p].r<=r)return t[p].p;
	int mid=t[p].l+((t[p].r-t[p].l)>>1);
	double ans=0;
	if (l<=mid)
		{
			ans=max(ans,ask(l,r,p<<1));
		}
	if (r>mid)
		{
			ans=max(ans,ask(l,r,p<<1|1));
		}
	return ans;
}

int32_t main()
{
	int n,m,q,r,s,k;
	int maxn=0;
	double p;
	cin>>n>>m>>q;
	build(1,N-1,1);//先建立空树，再每个点补进去，毕竟整棵树不适合建立时一个点一个点带入
	for (int i=1; i<=n; ++i)
		{
			cin>>p>>r;
			if (!mp[p])mp[p]=i,mp1[p]=r;
			else if (mp1[p]>a[i];
	sort(a+1,a+1+m,cmp);
	while (q--)
		{
			cin>>s>>k;
			int tmp=max(a[k]-s,1ll);
			if (tmp>maxn)
				{
					cout<<-1<

H-跳台滑雪 II

思路：

1.  首先，他要求的是i个动作选k个获得的最大分数——这不就裸背包吗

2. 然后呢，期望怎么办

   1. 选x的期望是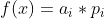,选x，y两个呢？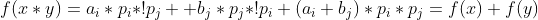

   2. 所以选某个动作时，直接加上他的期望即可 
3. 我们可以用dp[j][h]表示在j分数下选了k个动作时的期望，每次更新dp[j][h],对于当前动作a[i]，在选了h-1个动作的前提下,比较不选这个动作（即还是dp[j][h]）大，还是选了这个动作，在原来分数为j-a[i],选了h-1个动作时，使用a[i]获得的期望（即dp[j-a[i]][h-1]+a[i]*p[i])哪个大

#include 
using namespace std;
#define ll               long long
#define endl             "\n"
#define int              long long
const int N = 1e5 + 10;
int a[N];
double p[N];
void mysolve()
{
	int n,k;
	double m;
	cin>>n>>k>>m;
	vector>dp(100*k+1,vector(k+1,-1));
	dp[0][0]=0;
	for (int i=1; i<=n; ++i)
		cin>>a[i]>>p[i];
	//j逆序，避免重复选a[i]，h当然也要逆序，不然你这h-1个就可能是同一个了（都是避免后效性）
	for (int i=1; i<=n; ++i)for (int j=k*100; j>=a[i]; --j)for (int h=min(i,k); h>=1; --h)
				{
					if (dp[j-a[i]][h-1]!=-1)//期望不为-1，说明有这个数
						{
							dp[j][h]=max(dp[j][h],dp[j-a[i]][h-1]+a[i]*p[i]);
						}
				}
	for (int j=100*k; j>=0; --j)
		{
			if (dp[j][k]>=m)//找到最大分数且期望大于要求m
				{
					printf("%lld %.2lf\n",j,dp[j][k]);
					return ;
				}
		}
	printf("0 0.00\n");
}
int32_t main()
{
	ll t;
	cin >> t;
	while (t--)
		{
			mysolve();
		}
	system("pause");
	return 0;
}

J-RGB

思路：

1. 我们注意到m才为8（即每一列最多8个元素），如果我们暴力枚举一列可能出现的状态，二维不就变成了一维的简单dp转移方程了吗。
2. 我们的处理是
   1. 首先dfs暴力出一列的所有状态
   2. 然后对于每一个状态，求出哪些状态可以跟他相邻
   3. 那么我们设dp[i][j]表示已经已经求了i-1列，求第i列状态为j时数量。设in[j]表示可以与j相邻的状态
3. 所以他就是i-1列所有可以与他相邻状态的和 
4. 最后答案就是n列每个状态的和

#include 
using namespace std;
#define ll     long long
const int N = 1e4 + 10;
const int mod=1e9+7;
int n,m;
sets;
mapmp;
int cnt;
vectorin[N];
int dp[N][N];
void dfs(string p,int num)
{
	if (num==n)//求出每一列可能的状态
		{
			s.insert(p);
			mp[p]=++cnt;//mp把字符串转化为数字
			return;
		}
	for (int i=0; i<3; ++i)
		{
			char c=i+'0';
			if (num>0&&p[num-1]==c)continue;
			string tmp=p+c;
			dfs(tmp,num+1);
		}
}
bool myjud(string a,string b)//判断是否可以相邻
{
	for (int i=0; i>n>>m;
	dfs("",0);
	for (auto &a:s)for (auto &b :s)
			{
				if (myjud(a,b))in[mp[a]].push_back(mp[b]);//求出每个状态可以与他相邻的状态
			}
	for (int i=1; i<=cnt; ++i)dp[1][i]=1;//显然，只有1列，每个状态只有一种情况
	for (int i=2; i<=m; ++i)for (int j=1; j<=cnt; ++j)for (auto &k:in[j])dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;//求和
	int ans=0;
	for (int i=1; i<=cnt; ++i)ans=(ans+dp[m][i])%mod;
	cout<