有序序列查找-斐波那契查找(Fibonacci Search)

有序序列查找-斐波那契查找(Fibonacci Search)

1. 前言

如果数组为有序表或有序数列，查找函数可以采用斐波那契查找实现。斐波那契查找与折半查找（二分查找）的最大区别是，斐波那契查找函数对有序表进行分对称分割，而折半查找则是对有序表进行对对称分割；另外斐波那契查找的位置确定仅涉及到加减运损，而折半查找则涉及到除法运算；研究表明斐波那契搜索在后续步骤中检查相对接近的元素，因此，当输入数组很大，无法放入 CPU 缓存甚至 RAM 时，斐波那契搜索会派上用场。

斐波那契查找本质上是对有序表进行分而治之，先对原来数组进行分裂处理，进而找到待查找元素所属的子区间，后面反复进行处理，直至找到查询的对象或查询失败。

2. 算法分析

算法的关键是找到合适的分割点，这些分割点隶属于某个斐波那契数，所以问题转化为，每次分治前，需要寻找到合适的斐波那契数字。为了查询方便，我们可以引入Fib数组，这个数组中储存的最大斐波那契数字恰好大于数组中元素的个数，也就是Fib[u]>n，其中u为的最小的下标值，定义u为查询问题中Fib数组的上界(upper bound)。

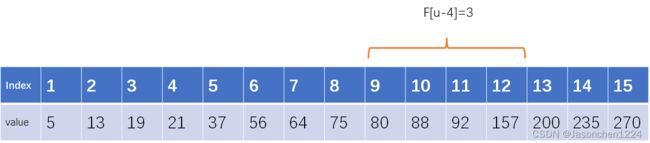
先看一个具体的例子，给定有序数列，数列中包含15个元素，并且元素为有序递增排列。

在此条件下，我们就要寻找斐波那契数字，斐波那契的值需要大于15的最小值，显而易见21为我们需要搜索的具体值，上界下标的值(upper bound)u等于7。

假定要寻找目标数字等于88，第一个分割点位置为low+F[u-1]，那么其左边元素个数不超过F[u-2]，右半部分元素数量不超过F[u-3]，由于右半部分的分割点的值可能大于最高点位置，所以mid在这里就需要取low+F[u-1]-1和high之间的最小值，确保mid值不越界。

3. 搜索过程

假定搜索目标为88，那么第一次分割，选择左半部分，继续搜索，

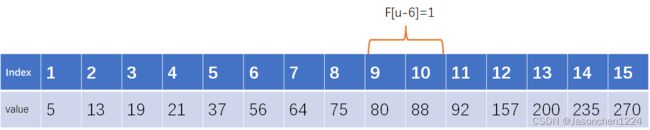
第二次分割后，88属于右半部分，

第三次分割后，88属于左半部分，

此时mid=10，所以查询结束。

4. 代码实现

代码的数据结构参考清华大学严蔚敏的《数据结构（C语言版）》的基本数据类型，利用这些数据类型构建查询表(Search Table)，构造数据类型过程中利用到文件指针的相关知识，在此不再赘述。

代码分为三个关键函数，第一部分是寻找斐波那契的下标的上界值和构建斐波那契数组：

第一部分为头文件定义

/**
 * @file Fib_search.h
 * @author your name ([email protected])
 * @brief 
 * @version 0.1
 * @date 2023-04-08
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef FIB_SEARCH_H
#define FIB_SEARCH_H
#include 
#include 
#include 
#include "../00_introduction/Status.h"

#define EQ(a,b) ((a)==(b))
#define LT(a,b) ((a)<(b))
#define LQ(a,b) ((a)<=(b))

#define MAX_LEN 20

typedef int   KeyType;
typedef char* Record;


typedef struct  SElemType
{
    KeyType key;
    Record  value;
}SElemType;

typedef struct SSTable
{
    SElemType *elem;
    int        len;
} SSTable;

void CreateTable(FILE *fp, SSTable *st);



int fib_search_iteration(SSTable st, KeyType key,int u, int *fib);


int find_upper_bound(SSTable st,int **fib);


int min(int a, int b);


#endif

第二部分关键函数的实现

/**
 * @file Fib_search.c
 * @author your name ([email protected])
 * @brief 
 * @version 0.1
 * @date 2023-04-08
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef FIB_SEARCH_C
#define FIB_SEARCH_C
#include "Fib_search.h"

void CreateTable(FILE *fp, SSTable *st)
{
    int n;
    char str[MAX_LEN];
    int i;


    n=0;
    // 当读取 (n-1) 个字符时，或者读取到换行符时，或者到达文件末尾时，它会停止，具体视情况而定。
    while(fgets(str,MAX_LEN,fp)!=NULL)
    {
        n++;
    }

    fseek(fp,0,SEEK_SET);

    st->len=n;
    st->elem=(SElemType *)malloc(sizeof(SElemType)*(n+1));

    for(i=1;i<=n;i++)
    {
        st->elem[i].value=(Record)malloc(sizeof(char)*MAX_LEN);
        memset(st->elem[i].value,0,sizeof(char)*MAX_LEN);
        fscanf(fp,"%d %s",&(st->elem[i].key),st->elem[i].value);
    }

    return;    
}

int find_upper_bound(SSTable st, int **fib)
{
    int n;
    int u;
    int i;
    int max_num=10;
    int dp[max_num];

    dp[0]=1;
    dp[1]=1;
  
    n=st.len;

    for(i=2;i<max_num;i++)
    {
        dp[i]=dp[i-1]+dp[i-2];

        if(dp[i]>n)
        {
            break;
        }
    }

    *fib=(int *)malloc(sizeof(int)*(i+1));

    memcpy(*fib,dp,sizeof(int)*(i+1));

    return i;
}

int fib_search_iteration(SSTable st, KeyType key, int u, int *fib)
{
    int low;
    int high;
    int mid;
    int index;

    low=1;
 
    high=st.len;
    index=u-1;

    while(low<=high && index>=0)
    {
        mid=min(low+fib[index]-1,high);

        // 1、1、2、3、5、8、13、21、34
        if(EQ(key,st.elem[mid].key))
        {
            return mid;
        }
        else if (LT(key, st.elem[mid].key))
        {
            high=mid-1;
            index=index-1;
        
        }
        else
        {
            low=mid+1;
            index=index-2;     
        }
     
    }

    if (low==high && EQ(key, st.elem[low].key) && index <0)
    {
        return low;
    }
    else
    {
        return 0;
    }
}

int min(int a, int b)
{
    return (a<b?a:b);
}

#endif

第三部分为测试函数

/**
 * @file Fib_search_main.c
 * @author your name ([email protected])
 * @brief 
 * @version 0.1
 * @date 2023-04-08
 * 
 * @copyright Copyright (c) 2023
 * 
 */
#ifndef FIB_SEARCH_MAIN_C
#define FIB_SEARCH_MAIN_C
#include "Fib_search.c"

int main(void)
{
    FILE *fp;
    KeyType key_1=88;
    KeyType key_2 = 85;
    SSTable st;
    int u;
    int index_1;
    int index_2;
    int *fib;

    fp=fopen("data.txt","r");
    CreateTable(fp,&st);

    // 1,1,2,3,5,8,13,21,34
    u=find_upper_bound(st,&fib);

    index_1=fib_search_iteration(st,key_1,u,fib);
    //index_2=fib_search_recursion(1,st.len,st,key_1,u,fib);
    

    printf("The index is %d and %d\n",index_1,index_2);
    
    getchar();
    return EXIT_SUCCESS;
}


#endif

data.txt文件

5 fox
13 the
19 jump
21 out
37 box
56 it
64 looks
75 very
80 sad
88 do
92 feel
157 good
200 bad
235 june
270 nice

5. 小结

通过本问题的分析，对斐波那契搜索方法有了更进一步的认识，同时理解斐波那契搜索为非对称搜索，在过程中可能产生越界，处理越界称为本搜索问题的关键。

参考资料：

1. Fibonacci Search - GeeksforGeeks